Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 5 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 5 with Solutions
Time Allowed: 2 Hours
Maximum Marks: 40
General Instructions:
- There are 12 questions in all. All questions are compulsory.
- This question paper has three sections: Section A, Section B and Section C.
- Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
- There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
- You may use log tables if necessary but use of calculator is not allowed.
SECTION – A
(Section A contains 3 questions of 2 marks each.)
Question 1.
Explain the formation of secondary rainbow. (2)
Answer:
It is the result of fur-step process. Refraction with dispersion followed by internal reflection, and finally reflection.
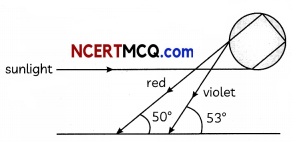
It is found that red light emerges at an angle of 50° related to the incoming sunlight and violet light emerges at an angle of 53°. Thus, the observer sees secondary rainbow with violet colour on top and red colour on the bottom. The intensity of light is reduced at second internal reflection and hence it is fainter than primary rainbow.
![]()
Question 2.
What is the shape of fringe pattern on the screen? (2)
Answer:
The locus of point P in the plane of the screen, such that S2P-SiP is a constant, is a hyperbola. Thus, fringe pattern are hyperbola.
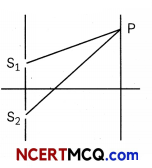
Question 3.
A parallel beam of light of 450 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1.5 m away. It is observed that the first minimum is at a distance of 3 mm from the centre of the screen. Calculate the width of the slit.
OR
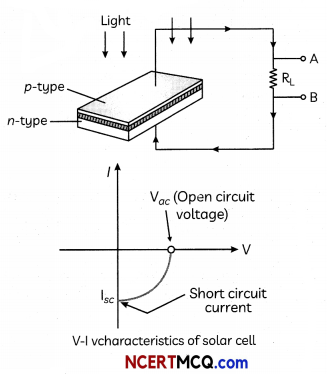
Draw the diagram of a solar cell and draw its V-l characteristics. (2)
Answer:
The distance of the nth minimum from the centre of the screen,
Xn = \(\frac{n \mathrm{D} \lambda}{a}\)
Where, D → distance of slit from
screen
λ → wavelength of the light
a → width of the slit
For first minimum,
n = 1,
Xn = 3 × 10-3 m
D = 1.5 m
λ = 450 × 10-9m
3 × 10-3 = \(\frac{1 \times(1.5) \times\left(450 \times 10^{-9}\right)}{a} \frac{n D \lambda}{a}\)
a = \(\frac{1 \times(1.5) \times\left(450 \times 10^{-9}\right)}{3 \times 10^{-3}}\)
a = 0.255 mm
OR
Caution
V-I characteristics of solar cell is drawn in fourth quadrant of the coordinate axes, This is because a solar cell does not draw current but supplies the same to the load.
![]()
SECTION – B
(Section B consists of 8 questions of 3 marks each.)
Question 4.
The trajectories, traced by different a-particles, in Geiger Marsden experiment were observed as shown in the figure.
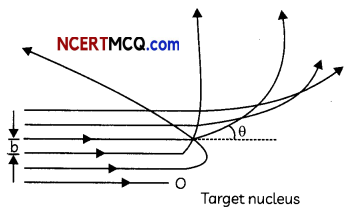
(A) What names are given to the symbols ‘b’ and ‘θ’ shown here.
(B) What can we say about the values of b for
(i) θ = 0°
(ii) θ = π radians. (3)
Answer:
(A) The smbo1b’ represents impact parameter and ‘θ’ represents the scattering angle.
(B) (i) When θ = 0o. the impact parameter will be maximum and represent the atomic size.
(ii) When θ = π radians, the impact parameter ‘b’ will be minimum and represent the nuclear size.
Question 5.
Draw reflected or refracted wavefront when a plane wavefront is incident on prism, convex lens and concave mirror.
OR
What difference between an intrinsic semiconductor and p-type extrinsic semiconductor? Why p-type semiconductor is electrically neutral even if number of holes are larger than the number of electrons? (3)
Answer:
(A) (i) When a plane wave is incident on prism
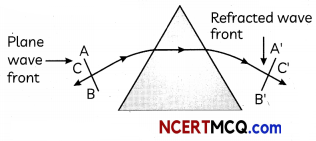
(ii) Convex lens
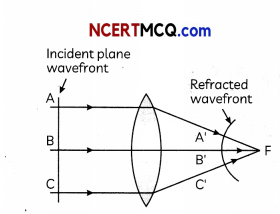
(iii) Concave mirror
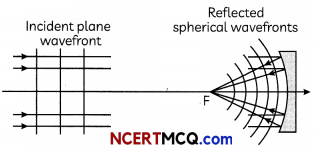
OR
| Intrinsic Semiconductors | p-Type Extrinsic Semiconductor |
| These pure semiconducting materials and known variety is added to them. They have equal number of holes and electrons. | These are prepared by doping a small quantity of impurity of trivalent material to the pure semiconductor material which results in higher number of holes compared to electrons. |
| The electrical conductivity is generally small. | The electrical conductivity is comparatively very high. |
A p-type semiconductor crystal is electrically neutral because the charge of additional charge carriers is just equal and opposite to that of the ionized cores in the crystal lattice.
![]()
Question 6.
(A) Monochromatic light of frequency 6.0 × 1014 Hz is produced by a laser. The power emitted is 2.0 × 10-3 W. Estimate the number of photons emitted per second on an average by the source.
(B) Draw a plot showing the variation of photoelectric current versus the intensity of incident radiation on a given photosensitive surface. (3)
Answer:
(A) The energy of a photon of frequency v is
E = hv
= (6.63 × 10-34 Js) × (6 × 1014 s-1)
= 3.98 × 10-19 J = 4 × 10-19J
If n be the number of photons emitted by the source per second, then the power P transmitted in the beam is given by,
P = nE
∴ n = \(\frac{P}{E}\)
⇒ n = \(\frac{2 \times 10^{-3}}{4 \times 10^{-19}}\)
5 × 1015 photons/sec
Related Theory
Photoelectric current is directly proportional to the intensity of incident radiation.
Question 7.
The oscillating magnetic field in a plane electromagnetic wave is given by:
By = (8 × 10-6) sin[2 × 1011t + 300π X]T
(A) Calculate the wavelength of the electromagnetic wave.
(B) Write down the expression for the oscillating electric field. (3)
Answer:
(A) Comparing above equation by the standard equation of magnetic field is:
By = B0 sin(ωt + kx)T
We get B0 = 8 × 10-6 T,
ω = 2 × 1011 rad/s,
k = \(\frac{2 \pi}{\lambda}\) = 300π
Wavelength
λ = \(\frac{2 \pi}{300 \pi}\)
= \(\frac{1}{150}\) m = 6.67 mm
(B) E0 = B0C
= 8 × 10-6 × 3 × 108
= 2.4 × 103V/m.
According to right hand system of vector E, vector B, vector K, the electric field oscillates along negative Z-axis, so equation is
Ez = -2.4 × 103sin(2 × 1011t + 300π X)\(\frac{\mathrm{V}}{\mathrm{m}}\)
![]()
Question 8.
(A) Write the relationship between angle of incidence ‘F, angle of prism ‘A’ and angle of minimum deviations δm for a triangular prism.
(B) A ray of light suffers minimum deviation, while passing through a prism of refractive index 1.5 and refracting angle 60°. Calculate the angle of deviation and angle of incidence. (3)
Answer:
(A) The relation between the angle of incidence i, angle of prism A, and the angle of minimum deviation δm, for a triangular prism is given by
i = \(\frac{\left(A+\delta_{m}\right)}{2}\)
(B) Here,
μ = 1.5,
A = 60°,
δm = ?
In the position of minimum deviation
I = \(\frac{A+\delta_{m}}{2}\),
r = \(\frac{\mathrm{A}}{2}\)
As
μ = \(\frac{\sin i}{\sin r}\)
∴ 1.5 = \(\frac{\sin i}{\sin 30^{\circ}}\)
⇒ sin i = 1.5 × 0.5
= 0.75
⇒ i = sin-1 (0.75)
= 48.60°
δm = 2i – A
= 2 × 48.6 – 60 = 37.2°
![]()
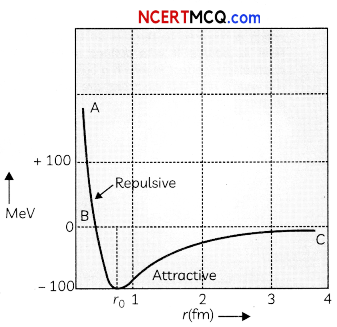
Question 9.
(A) In a nuclear reaction
\({ }_{2}^{3} \mathrm{He}\) + \({ }_{2}^{3} \mathrm{He}\) → \({ }_{2}^{4} \mathrm{He}\) + \({ }_{1}^{1} \mathrm{He}\) + \({ }_{1}^{1} \mathrm{He}\) + 12.86 MeV though the number of nucleons is conserved on both sides of the reaction, yet the energy is released. How ? Explain. (B) Draw a plot of potential energy between a pair of nucleoni as a function of their separation. Mark the regions where
potential energy is
(i) positive and
(ii) negative. (3)
Answer:
(A) in a nuclear reaction, the sum of the masses of the target nucleus \({ }_{2}^{3} \mathrm{He}\) may be greater or less then sum of the masses of the product nucleus \({ }_{2}^{4} \mathrm{He}\) and the \({ }_{1}^{1} \mathrm{He} .\) So from the law of conservation of mass energy, some energy, (12.86 MeV) is evolved in nuclear reaction. This energy is called Q-value of the nuclear reaction. The binding energy of the nucleus on the left side is not equal to the right side. The difference in the binding energies on two sides appears as energy released or absorbed in the nuclear reaction.
(B) The potential energy is minimum at to- For distance larger than r0 the negative potential energy goes on decreasing and for the distances Less than r0 the negative potential energy decrease to zero and then becomes positive and increases abruptly. Thus, A to B is the positive potential energy region and B to C is the negative potential energy region.
Question 10.
(A) Give the significance of the sentence “a light ray, while undergoing refraction at the interface of two media, bends towards the normal in the second media”.
(B) Diameter of a plano-convex lens is 6 cm and thickness at the centre is 3 mm. If speed of light in material of lens is 2 × 108 m/s. Find the focal length of the lens? (3)
Answer:
(A) The second medium is optically denser with respect to first medium and speed of Light in second medium is less.
(B)
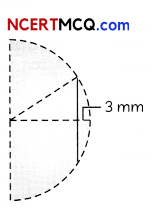
n = \(\frac{3}{2}\) [∵ n = \(\frac{C}{V}\)]
32 + (R – 3 mm)2 = R2
⇒ 32 + R2 – 2R (3 mm) + (3 mm)2 = R2
⇒ R ≈ 15 cm
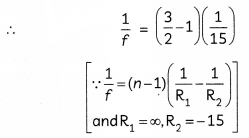
⇒ f = 30 cm
Caution
Students are often confused to find the value ofR. In this question they have to use Pythagoras theorem.
![]()
Question 11.
The ground state energy of hydrogen atom is -13.6 eV. If an electron makes a transition from an energy level -0.85 eV to -1.51 eV, calculate the wavelength of the spectral line emitted. To which series of hydrogen spectrum does this wavelength belong?
OR
Give reasons for the following:
(A) Why semiconductor diodes are preferred over vacuum diodes?
(B) A photodiode, when used as a detector of optical signals is operated under reverse bias.
(C) The band gap of the semiconductor used for fabrication of visible LEDs must be at least 1.8 eV. (3)
Answer:
As we know, En = \(\frac{-13.6}{n^{2}}\)eV …………. (i)
For n = 1, E1 = – 13.6 eV
When electron undergoes transition from EA = – 0.85 eV Then, from equation (i),
– 0.85 = – \(\frac{13.6}{n_{A}^{2}}\) ⇒ nA = 4
Similarly, -1.51 = \(\frac{-13.6}{n_{B}^{2}}\) ⇒ nB
Hence, electron transits from n = 4 to n = 3 which corresponds to Paschen series of hydrogen atom.
As, \(\frac{1}{\lambda}\) = R(\(\frac{1}{n_{B}^{2}}-\frac{1}{n_{A}^{2}}\))
Here nA = 4, nB = 3, R = 1.0974 × 107
Then \(\frac{1}{\lambda}\) = 1.097 × 107(\(\frac{1}{3^{2}}-\frac{1}{4^{2}}\))m-1
⇒ λ = 1875 nm
OR
(A) In semiconductor diodes, no cathode heating is required in junction diode for production of charge carriers. Voltage drop across a junction diode is much less compared to that across a vacuum diode. Semiconductor diodes can be used for much higher frequencies.
(B) When operated under reverse bias, the photodiode can detect changes in current with changes in light intensity more easily because the fractional change in minority charge carriers is more than that in majority charge carriers.
(C) The Photon energy, visible light photons vary from about 1.8 eV to 3 eV. Hence for visible LEDs, the semiconductor must have a band gap of 1.8 eV.
![]()
SECTION – C
(Section C consists one case study-based question of 5 marks.)
Question 12.
Wave theory of light was followed while explanation of photoelectric effect. There were many failures of wave theory of light. According to wave theory when light incident on a surface, energy is distributed continuously over the surface. So that electron must take a time interval to accumulate suffiicient energy to come out. But in experiment there is no time lag. When intensity is increased, more energetic electrons should be emitted. So that stopping potential should be intensity dependent. But it is not observed. According to wave theory, if intensity is suffiicient then, at each frequency, electron emission is possible. It means there should not be existence of threshold frequency.
(A) The stopping potential necessary to reduce the photoelectric current of zero:
(i) is directly proportional to wavelength of incident light.
(ii) uniformly increases with the wavelength of incident light.
(iii) directly proportional to frequency of incident light.
(iv) uniformly increases with the frequency of incident light.
(B) The photoelectric threshold frequency of a material is u. When light of frequency 4 u is incident on the metal, the maximum kinetic energy of the emitted photoelectron is:
(i) \(\frac{5}{2}\)hu
(ii) 3 hu
(iii) 4 hu
(iv) 5 hu
(C) When photons of energy hv fall on an aluminium plate (of work function Eo), photoelectrons of maximum kinetic energy K are ejected. If the frequency of radiation is doubled, the maximum kinetic energy of the ejected photoelectrons will be:
(i) K + hv
(ii) K + E0
(iii) 2K
(iv) K
(D) To understand photoelectric effect a graph is plotted between two factors, which is a straight line. The factors are:
(i) Intensity of radiation and photoelectric current
(ii) Potential of anode and photoelectric current
(iii) Threshold frequency and velocity of photoelectrons
(iv) Intensity of radiation and stopping potential.
(E) Light of wavelength 5000 Å falls on a sensitive plate with photoelectric work function 1.9 eV. The maximum kinetic energy of the photoelectrons emitted will be:
(i) 0.58 eV
(ii) 2.48 eV
(iii) 1.24 eV
(iv) 1.16 eV (5)
Answer:
(A) (d) uniformly increases with the frequency of incident light
Explanation: The negative potential at which photoelectric current becomes zero is called stopping potential.
By eVs = hv – Φ
Stopping potential required to reduce the photoelectric current to zero “decreases uniformly with the frequency of the incident radiation”.
(B) (b) 3hu
Explanation: The maximum kinetic energy of the emitted electrons is given by Kmax = hu-Φ0
= h(4u) – h(u) = 3hu
Related Theory
Maximum kinetic energy of the emitted electron = hv – Φ0
(C) (a) K + hv
Explanation: Let K and K’ be the maximum kinetic energy of photoelectrons for incident light of frequency v and 2v respectively. According to Einstein’s photoelectric equation,
K = hv – E0 ………….. (i)
and K’ = h(2v) – E00 ………….. (ii)
= 2hv – E0 = hv + hv – E0
K’ = hv + K [using (i)]
![]()
Related Theory
The kinetic energy of the emitted electrons is given by K= hv – Φ0
(D) (a) Intensity of radiation and photoelectric current
Explanation: Intensity of radiation linearly changes the photoelectriccurrent. Photoelectric current ∝ intensity of radiation.
Caution
Students are often confused about the relation between photoelectric current and intensity of radiation. They are directly proportional to each other.
(E) (a) 0.58 eV
Explanation: hv = \(\frac{h c}{\lambda}\)
= \(\frac{1240}{500}\)
= 2.48 eV
\(\frac{1}{2}\) mvmax2 = hv – Φ0 = 2.48 – 1.90
= 0.58 eV
Related Theory
Work function is as the minimum amount of energy which is required to remove an electron to infinity from its source. It was defined in the concept of photoelectric effect in which a light is incident upon the metal and the electrons are ejected from the metal.