CBSE Sample Papers for Class 12 Physics Term 2 Set 9 with Solutions

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 9 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 9 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• There are 12 questions in all. All questions are compulsory.
• This question paper has three sections: Section A, Section B and Section C.
• Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
• There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
• You may use log tables if necessary but use of calculator is not allowed.

SECTION – A
(Section A contains 3 questions of 2 marks each.)

Question 1.
Number of protons and number of neutrons are same on either side of a nuclear reaction. Then how is it said that energy released in a nuclear reaction is due to conversion of mass.
OR
What is a p-n junction diode and define the term dynamic resistance for the junction diode? (2)
Answer:
Total binding energy of nuclei on one side of the nuclear reaction may not be equal to that on the other side of the reactions. This fact tells that only rest mass of neutrons and protons is same on each side of the reaction difference in total binding energy on both sides can be referred to as difference in total mass in a nuclear reaction.
OR
A p-n junction diode is a single crystal of Germanium or Silicon doped in such a manner that one half portion of it acts as a p-type semiconductor and other half acts as a n-type semiconductor. As soon as a p-n junction is formed, holes from p-region and electrons from n-region diffuse which results in development of potential barrier across the junction and opposes the further diffusion of holes and electrons through the junction.
The dynamic or alternating current resistance of diode is the ratio of small applied voltage to the corresponding change in current.
r_d = \(\frac{\Delta V}{\Delta l}\)
Above the threshold voltage, the diode characteristic is linear. In linear region, dynamic resistance is almost independent of voltage and Ohm’s law is obeyed.

Question 2.
Find the maximum intensity in case of interference of n identical waves each of intensity l0 if the sources are:
(A) Coherent
(B) Incoherent (2)
Answer:
(A) Coherent sources
Let the amplitude be A for each wave then,
A_R = (A + A + …)n times ,
= nA
lR ∝\(\) = n²l₀

(B) Incoherent Sources
l = l₀ + l₀…. )n times
= nl₀

Question 3.
State principle of reversibility of light. Define lateral shift. (2)
Answer:
Principle of reversibility of light states that if the final path of ray of light after it has suffered several reflections and refractions is reversed, it retraces its path exactly.

Lateral shift is the perpendicular distance between the incident and emergent rays when light is incident obliquely on a refracting slab with parallel faces.

SECTION – B
(Section B consists of 8 questions of 3 marks each.)

Question 4.
Answer the following questions:
(A) In a double slit experiment using light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
(B) Light of wavelength 5000 A propagating in air gets partly reflected from the surface of water. How will the wavelengths and frequencies of the reflected and refracted light be affected?
OR
(A) Describe any two characteristic features which distinguish between interference and diffraction phenomena. Derive the expression for the intensity at a point of the interference pattern in Young’s double slit experiment. (3)
Answer:
(A) Angular width (θ) of fringe in double-slit experiment is given by
θ = \(\frac{\lambda}{d}\)
Where d = Spacing between the slits.
Given: Wavelength of light,
λ = 600 nm
Angular width of fringe,
θ = 0.1°
= 0.1 × \(\frac{\lambda}{180}\) rad
= 0.0018 rad
∴ d = \(\frac{\lambda}{\theta}\)
d = \(\frac{600 \times 10^{-9}}{18 \times 10^{-4}}\) = 33.33 × 10^-5
⇒ d = 0.33 × 10^-3 m

(B) The frequency and wavelength of reflected wave will not change.
The refracted wave wiLl have same frequency, only wavelength will change.
The velocity of light v in water is given by
v = λf
where, v = Velocity of light
f = Frequency of light
λ = Wavelength of light As light ray in travelling from rarer (air) medium to denser medium, its speed will decrease. Hence wavelength (λ) will also decrease.

ReLated Theory
When a light ray traveLs from rarer medium to denser medium, then its speed and wavelength both will decrease.
(A)

Interference	Diffraction
1. It is the result of interaction of light coming from two different wave fronts originating from two coherent sources.	1. It is the result of interaction of light come from different parts of same wavefronts.
2. All the bright fringes are of same intensity.	2. The bright fringes are of varying intensity (Intensity of bright fringes decreases from central bright fringe on either sides.)

A sources of monochromatic light illuminates two narrow slits S₁ and S₂. The two illuminated slits act as the two coherent sources. The two slits is very close to each other and at equal distance from source. The wave front S₁ and S₂ spread in all direction and superpose and produces dark and bright fringe on screen. Let the displacement of waves from Si and S2 at point P on screen at time t is:

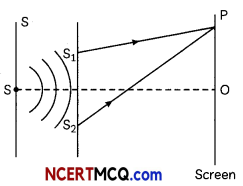
y₁ = a₁sin ωt
y₂ = a₂ sin (ωt + Φ)
The resultant displacement at point P is given by
y = y₁ + y₂
= a₁ sin ωt + a₂ sin (ωt + Φ)
= a₁ sin ωt + a₂ sin ωt cos Φ
+ a₂ cos ωt sin Φ
= (a₁ + a₂ cos Φ) sin ωt + a₂ sin Φ cos ωt …………. (i)
Let, a₁ + a₂ cos Φ
= A cos Φ …………. (ii)
a₂ sin Φ = A sin Φ …………. (iii)

Therefore, equation (i) becomes
y = A cos θ sin ωt + A sin θ cos ωt
= A sin (ωt + θ)
This is the resultant displacement.
Now, squaring and adding equations (ii) and (iii)
A² cos² θ + A² sin²θ
= (a₁ + a₂ cos Φ)² + a₂² sin² Φ
A² = a₁² + a₂² + 2a₁ a₂ cos Φ

The is intensity of light is directly proportional to the square of the amplitude
i.e., I = a₁² + a₂² + 2a₁ a₂ cos Φ

This is the expression for intensity at a point of interference pattern.
or I = I₁+ I₂ + \(2 \sqrt{I_{1} I_{2}}\) cos Φ

Question 5.
(A) On what factor does the velocity of EM waves depends on?
(B) The magnetic field in a travelling
electromagnetic wave has a peak value of 20 nT. Find the peak value of electric field strength? (3)
Answer:
(A) The velocity of electromagnetic wave
depends on electric and magnetic properties of the medium.

(B) Here,
B₀ = 20nT
= 20 x 10^-9T,
c = 3 x 10⁸ m/s
E₀ = cB₀
= 3 x 10⁸ x 20 x 10^-9
= 6 V/m

Question 6.
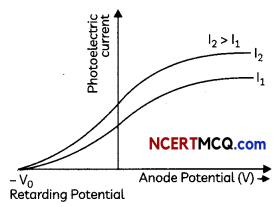
(A) Draw graphs showing variation of photoelectric current with applied voltage for two incident radiations of equal frequency and different intensities. Mark the graph for the radiation of higher intensity.
(B) An α-particle and a proton are accelerated through the same potential difference. Find the ratio of their de Broglie wavelengths. (3)
Answer:
(A) Graph for photoelectric current (I) versus applied potential for radiations of same frequency and varying intensity.

(B)


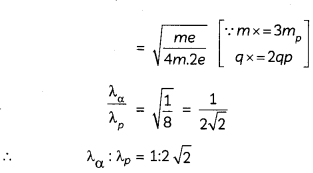
Caution
Students are often confused in solving this problem. Here, de-Broglie wavelength is inversely proportional to the square root of mass and charge.

Question 7.
What are the important considerations required while fabricating a p-n junction diode to be used as a light emitting diode? (3)
Answer:
(A) There is a very little resistance to limit the current in LED. Therefore, a resistor must be used in series with the LED to avoid any damage to it.

(B) The reverse breakdown voltage of LEDs is very low, typically around 5 V. Therefore, care should be taken while fabricating a p-n junction diode so that the p-side should only attached positive side of the battery as LED easily get damaged by small reverse voltage.

(C) The semiconductors used for fabrication of visible LEDs must have at least band gap of 1.8 eV.

Question 8.
(A) What is the position of an object
relative to the objective of compound microscope? Where is its image formed?
(B) The magnifying power of objective of compound microscope is 5. If the magnifying power of microscope is 30, then what is the magnifying power of eyepiece? (3)
Answer:
(A) When object is placed slightly larger than f₀ then the final image is formed at infinity.

(B) M = M₀ x M_e
Here, M = 30
and M₀ = 5
M_e = \(\frac{\mathrm{M}}{\mathrm{M}_{o}}\)
= \(\frac{30}{5}\) = 6

Question 9.
(A) How does the de-Broglie wavelength of a charged particle change when accelerating potential increases?
(B) A proton and an a-particle have the same de-Broglie wavelength. Determine the ratio of:
(A) their accelerating potentials.
(B) their speeds. – (3)
Answer:
(A) λ ∝ \(\frac{1}{\sqrt{V}}\), WhenV increases, λ decreases.

(B) (i) The de-Broglie wavelength of a particle is given by
λ = \(\frac{h}{\sqrt{2 m q V}}\)
where, V is the accelerating potential of the particle.
It is given that
λ_proton = λ_alpha
⇒ \(\frac{h}{2 m_{p} q_{p} V_{p}}\) = \(\frac{h}{2 m_{\alpha} q_{\alpha} V_{\alpha}}\)
\(\sqrt{2 m_{\alpha} q_{\alpha} V_{\alpha}}\) = \(\sqrt{2 m_{p} q_{p} V_{p}}\)
On squaring both sides, we get
2m_αq_αV_α = 2m_pq_pV_p
⇒ \(\frac{V_{p}}{V_{\alpha}}\) = \(\frac{m_{\alpha} q_{\alpha}}{m_{p} q_{p}}\)
= \(\frac{4 m_{p} \times 2 q_{p}}{m_{p} q_{p}}\)
[∵m_a = 4m_p and q_α = 2q_p]
= \(\frac{8}{1}\)

(B) We can also write de-Broglie wavelength as:
λ = \(\frac{1}{2 \pi f C}\)

where h is Planck’s constant, m is mass of the particle and v is the speed of the particle.
It is given that
λ_proton = λ_alpha
We know
m_alpha = 4m_proton
∴ λ_alpha = \(\frac{h}{4 m_{\text {proton }} V_{\text {alpha }}}\)
⇒ Now L
\(\frac{h}{m_{\text {proton }} v_{\text {proton }}}\) = \(\)
\(\frac{h}{4 m_{\text {proton }} v_{\text {alpha }}}\) = 4

Question 10.
Distinguish between intrinsic semiconductors
and extrinsic semiconductors. 3
Answer:

Intrinsic Semiconductors	Extrinsic Semiconductors
These ore pure semiconducting tetravaLent crystals.	These are conducting tetravalent crystals doped with impurity atoms of group III or V.
Their electrical conductivity is Low	Their electrical. conductivity is high.
There is no permitted energy state between valence and conduction bands.	There is permitted energy state of the impurity atom between vaLence and conduction bands.
The number of free electrons in the conduction band is equal to the number of hoLes in valence band.	The electrons are majority charge carriers in n-type semiconductors while hoLes are majority charge carriers in p-type semiconductors.
Their electrical conductivity depends on temperature.	Their electrical, conductivitçj depends on the temperature as well os on the dopant concentration.

Question 11.
(A) What is the maximum number of spectral lines emitted by a hydrogen atom when it is in the third excited state? (B) The velocity of electron in the first Bohr’s orbit of radius 0.5 A.U. is 2.25 x 106 m/s. Calculate the period of revolution of the electron in the same orbit
OR
What is a nuclear chain reaction? (3)
Answer:
(A) n = 4, number of maximum transition
= \(\frac{n}{2}\) (n – 1)
= 6

(B) Here, r = 0.5A.U.
= 0.5 × 1.5 × 10¹¹ m
[1 A.U. = 1.5 × 10¹¹ m]
v = 2.25 × 10⁶m/s
velocity of.electron in n^th orbit
\(\frac{1}{137}\) , \(\frac{c}{n}\)
Period of revolution
= \(\frac{2 \pi}{v}\)
= \(\frac{2 \pi r \times 137 \times n}{v}\)
= \(\frac{2 \times 3.14 \times 0.5 \times 1.5 \times 10^{11} \times 137 \times 1}{2.25 \times 10^{6}}\)
= 2.86 × 10⁸s
OR
The equation of fission of

These three secondary neutrons produced in the reaction may cause of fission of
three more (\({ }_{92}^{235} U\)) and give 9 neutrons, which in turn, may cause of nine more fission of (\({ }_{92}^{235} U\)) ar|d so on. Thus, a continuous ‘Nuclear Chain reaction would start. If there is no control on chain reaction then in a short time (~ 10^-6 sec.) a huge amount of energy will be released. (This is the principle of ‘Atom bomb’). If chain reaction is controlled then produced energy can be used for peaceful purposes. For examplenuclear reactor (Based on fission) generates electricity.

SECTION – C
(Section C consists one case study-based question of 5 marks.)

Question 12.
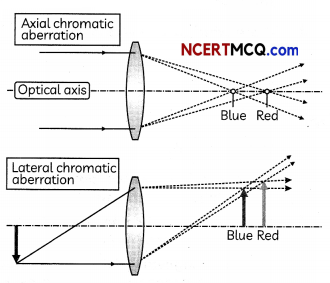
As the focal length of the lens varies from colour to colour, the magnification m = \(\)
produced by the lens also varies from colour to colour. Therefore, for little finite sized objects, the image due to different colours formed by the lens are of different sizes. The formation of images of different colours in different sizes is called lateral chromatic aberration.
Axial chromatic aberration

(A) An object is placed on the axis of a convex lens. Its image is formed 80 cm from the object. The magnification is 3. The focal length of the lens is:
(i) 15 cm
(ii) 20 cm
(iii) 40 cm
(iv) 45 cm

(B) The sun’s diameter is 1.4 x 10⁹ m and its distance from the earth is 10¹¹ m.
Determine the diameter of its image, formed by a convex lens of focal length 2 m.
(i) 0.7 cm
(ii) 1.4 cm
(iii) 2.8 cm
(iv) zero (i.e., point image)

(C) The combination of two lenses of focal lengths 20 cm and -20 cm in contact has the focal length of:
(i) 50 cm
(ii) Infinite
(iii) 10 cm
(iv) 60 cm

(D) Spherical aberration in thin lenses can be reduced by:
(i) Using monochromatic light
(ii) Increasing the size of the lens
(iii) Using a doublet combination
(iv) Using a circular annular mask over the lens.
(E) Two plano-convex lenses of equal focal lengths are arranged as shown. The ratio of combined focal length will be:

(i) 1:2:3
(ii) 1:1:1
(iii) 1:2:1
(iv) 2:1:2
Answer:
(A) (i)
Explanation:
m = \(\frac{v}{u}\)
v = 3u
u + v = 80 cm
> 4u = 80
u = 20 cm
v = 3 x 20 cm
= 60 cm
using \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
\(\frac{1}{f}\) = \(\frac{1}{60}-\frac{1}{(-20)}\)
f = 15 cm

Caution
Students are often confused about the sign convention. Remember that u is always negative.
(B) (Hi) 2.8 cm
Explanation: Magnification
m = \(\frac{h^{\prime}}{h}\)
= \(\frac{-v}{u}\)
or h’ \(\frac{-v}{u}\) x h
= \(\frac{-2 \times\left(1.4 \times 10^{9}\right)}{10^{11}}\)
= -2.8 cm

(C) (ii) Infinite
Explanation: Power = P₁
= \(\)
and p₂ = \(\)
= 5 D and -5D
Net power = 0
Therefore,
Focal length = \(\) = ∞

(D) (iv) Using a circular annular mask over the lens Explanation: In a thin lens, spherical aberration can be reduced by using a circular annular mask over the lens. It cuts off the marginal rays and focuses the par axial rays to a single point.

(E) (ii) 1:1:1
Explanation: The power of lens remains the same irrespective to the positioning of the lenses. So, the power and hence, their focal length in all three cases will remain the same.