Online Education for Circles Class 9 Extra Questions Maths Chapter 10 with Solutions Answers

Here we are providing Online Education Circles Class 9 Extra Questions Maths Chapter 10 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-9-maths/

Online Education Extra Questions for Class 9 Maths Circles with Answers Solutions

Extra Questions for Class 9 Maths Chapter 10 Circles with Solutions Answers

Circles Class 9 Extra Questions Very Short Answer Type

Circles Class 9 Extra Questions Question 1.
In the figure, O is the centre of a circle passing through points A, B, C and D and ∠ADC = 120°. Find the value of x.

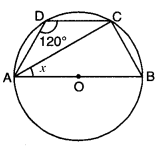
Solution:
Since ABCD is a cyclic quadrilateral
∠ADC + ∠ABC = 180°
[∴ opp. ∠s of a cyclic quad. are supplementary]
120° + ∠ABC = 180°
∠ABC = 180° – 120° = 60°
Now, ∠ACB = 90° [angle in a semicircle]
In rt. ∠ed ∆CB, ∠ACB = 90°
∠CAB + ∠ABC = 90°
x + 60° = 90°
x = 90° -60°
x = 30°

Class 9 Circles Extra Questions Question 2.
In the given figure, O is the centre of the circle, ∠AOB = 60° and CDB = 90°. Find ∠OBC.

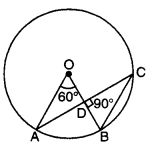
Solution:
Since angle subtended at the centre by an arc is double the angle
subtended at the remaining part of the circle.
∴ ∠ACB = \(\frac{1}{3}\) ∠AOB = \(\frac{1}{3}\) x 60° = 30°
Now, in ACBD, by using angle sum property, we have
∠CBD + ∠BDC + ∠DCB = 180°
∠CBO + 90° + ∠ACB = 180°
[∵ ∠CBO = ∠CBD and ∠ACB = ∠DCB are the same ∠s]
∠CBO + 90° + 30° = 180°
∠CBO = 180o – 90° – 30° = 60°
or ∠OBC = 60°

Circles Extra Questions Class 9 Question 3.
In the given figure, O is the centre of the circle with chords AP and BP being produced to R and Q respectively. If ∠QPR = 35°, find the measure of ∠AOB.

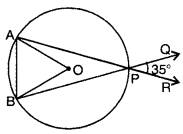
Solution:
∠APB = ∠RPQ = 35° [vert. opp. ∠s]
Now, ∠AOB and ∠APB are angles subtended by an arc AB at centre and at the remaining part of the circle.
∴ ∠AOB = 2∠APB = 2 × 35° = 70°

Circle Class 9 Extra Questions Question 4.
In the figure, PQRS is a cyclic quadrilateral. Find the value of x.

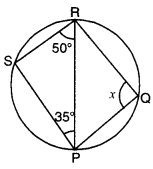
Solution:
In ∆PRS, by using angle sum property, we have
∠PSR + ∠SRP + ∠RPS = 180°
∠PSR + 50° + 35o = 180°
∠PSR = 180° – 85o = 95°
Since PQRS is a cyclic quadrilateral
∴ ∠PSR + ∠PQR = 180°
[∵ opp. ∠s of a cyclic quad. are supplementary]
95° + x = 180°
x = 180° – 95°
x = 85°

Extra Questions Of Circles Class 9 Question 5.
In the given figure, ∠ACP = 40° and BPD = 120°, then find ∠CBD.

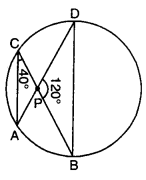
Solution:
∠BDP = ∠ACP = 40° [angle in same segment]
Now, in ∆BPD, we have
∠PBD + ∠BPD + ∠BDP = 180°
⇒ ∠PBD + 120° + 40° = 180°
⇒ ∠PBD = 180° – 160o = 20°
or ∠CBD = 20°

Extra Questions On Circles Class 9 Question 6.
In the given figure, if ∠BEC = 120°, ∠DCE = 25°, then find ∠BAC.

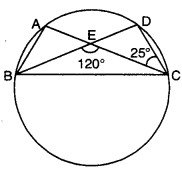
Solution:
∠BEC is exterior angle of ∆CDE.
∴ ∠CDE + ∠DCE = ∠BEC
⇒ ∠CDE + 25° = 120°
⇒ ∠CDE = 95°
Now, ∠BAC = ∠CDE [∵ angle in same segment are equal]
⇒ ∠BAC = 95°

Circles Class 9 Extra Questions Short Answer Type 1

Class 9 Maths Circles Extra Questions Question 1.
In the given figure, PQR = 100°, where P, Q and R are points on a circle with centre O. Find LOPR.

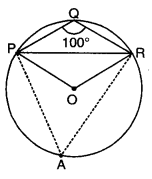
Solution:
Take any point A on the circumcircle of the circle.
Join AP and AR.
∵ APQR is a cyclic quadrilateral.
∴ ∠PAR + ∠PQR = 180° [sum of opposite angles of a cyclic quad. is 180°]
∠PAR + 100° = 180°
⇒ Since ∠POR and ∠PAR are the angles subtended by an arc PR at the centre of the circle and circumcircle of the circle.
∠POR = 2∠PAR = 2 x 80° = 160°
∴ In APOR, we have OP = OR [radii of same circle]
∠OPR = ∠ORP [angles opposite to equal sides]
Now, ∠POR + ∠OPR + ∠ORP = 180°
⇒ 160° + ∠OPR + ∠OPR = 180°
⇒ 2∠OPR = 20°
⇒ ∠OPR = 10°

Class 9 Maths Chapter 10 Extra Questions Question 2.
In figure, ABCD is a cyclic quadrilateral in which AB is extended to F and BE || DC. If ∠FBE = 20° and DAB = 95°, then find ∠ADC.

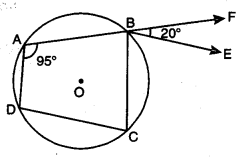
Solution:
Sum of opposite angles of a cyclic quadrilateral is 180°
∴ ∠DAB + ∠BCD = 180°
⇒ 95° + ∠BCD = 180°
⇒ ∠BCD = 180° – 95° = 85°
∵ BE || DC
∴ ∠CBE = ∠BCD = 85°[alternate interior angles]
∴ ∠CBF = CBE + ∠FBE = 85° + 20° = 105°
Now, ∠ABC + 2CBF = 180° [linear pair]
and ∠ABC + ∠ADC = 180° [opposite angles of cyclic quad.]
Thus, ∠ABC + ∠ADC = ∠ABC + 2CBF
⇒ ∠ADC = CBF
⇒ ∠ADC = 105° [∵ CBF = 105°]

Circles Class 9 Important Questions Question 3.
If the diagonals of a cyclic quadrilateral are diameters of the circle through the opposite vertices of the quadrilateral. Prove that the quadrilateral is a rectangle.
Solution:
Here, ABCD is a cyclic quadrilateral in which AC and BD are diameters.

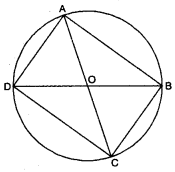
Since AC is a diameter.
∴ ∠ABC = ∠ADC = 90°
[∵ angle of a semicircle = 90°]
Also, BD is a diameter
∴ ∠BAD = ∠BCD = 90° [∵ angle of a semicircle = 90°]
Now, all the angles of a cyclic quadrilateral ABCD are 90 each.
Hence, ABCD is a rectangle.

Circle Extra Questions Class 9 Question 4.
Equal chords of a circle subtends equal angles at the centre.

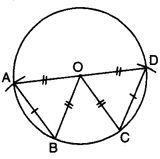
Solution:
Given : In a circle C(O, r), chord AB = chord CD
To Prove : ∠AOB = ∠COD.
Proof : In ∆AOB and ∆COD
AO = CO (radii of same circle]
BO = DO [radii of same circle]
Chord AB = Chord CD (given]
⇒ ∆AOB = ACOD [by SSS congruence axiom]
⇒ ∠AOB = COD (c.p.c.t.]

Extra Questions For Class 9 Maths Circles With Solutions Question 5.
In the figure, chord AB of circle with centre O, is produced to Csuch that BC = OB. CO is joined and produced to meet the circle in D. If ∠ACD = y and ∠AOD = x, show that x = 3y.

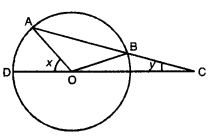
Solution:
In AOBC, OB = BC
⇒ ∠BOC = ∠BCO = y [angles opp. to equal sides are equal]

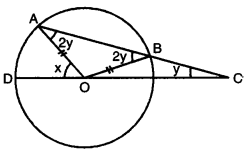
∠OBA is the exterior angle of ∆BOC
So, ∠ABO = 2y [ext. angle is equal to the sum of int. opp. angles]
Similarly, ∠AOD is the exterior angle of ∆AOC
∴ x = 2y + y = 3y

Questions On Circles For Class 9 Question 6.
In the given figure, P is the centre of the circle. Prove that : ∠XPZ = 2(∠X∠Y + ∠YXZ).

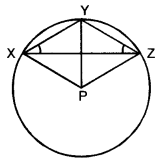
Solution:
Arc XY subtends ∠XPY at the centre P and ∠XZY in the remaining part of the circle.
∴ ∠XPY = 2 (∠X∠Y)
Similarly, arc YZ subtends ∠YPZ at the centre P and ∠YXZ in the remaining part of the circle.
∴ ∠YPZ = 2(∠YXZ) ….(ii)
Adding (i) and (ii), we have
∠XPY + ∠YPZ = 2 (∠XZY + ∠YXZ)
∠XP2 = 2 (∠XZY + ∠YXZ)

Circles Class 9 Extra Questions Short Answer Type 2

Circles Class 9 Extra Questions With Solutions Pdf Question 1.
In the given figure, AB and CD are two equal chords of a circle with centre O. OP and OQ are perpendiculars on chords AB and CD respectively. If ∠POQ = 120°, find ∠ APQ.

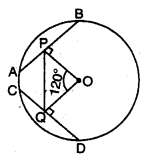
Solution: Since
AB = CD
∴ OP = OQ [∵ equal chords are equidistant from the centre]
∠OPQ = ∠OQP:
[by using isosceles triangle property, angles opp. to equal sides of a ∆]
In APOQ, by using angle sum property, we have
∠OPQ + ∠OQP + ∠POQ = 180°
⇒ ∠OPQ + ∠OPQ + 120° = 180°
⇒ 2∠0PQ = 60°
⇒ ∠OPO = 30°
Now, ∠APQ + ∠OPQ = 90°
⇒ ∠APQ + 30° = 90°
⇒ ∠APQ = 90° – 30o = 60°
Hence, ∠APQ = 60°

Class 9 Circles Extra Questions Pdf Question 2.
Two circles whose centres are O and O’ intersect at P. Through P, a line parallel to OO’, intersecting the circles at C and D is drawn as shown in the figure. Prove that CD = 2OO’.

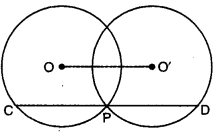
Solution:
Draw OA ⊥ CD and O’B ⊥ CD
Now, OA ⊥ CD
OA ⊥ CP
CA = AP = \(\frac{1}{2}\)CP
CP = 2AP ….(i)

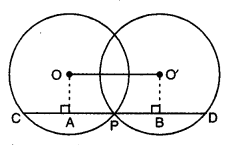
Similarly, O’B ⊥ CD
O’B ⊥ PD
⇒ PB = BD = \(\frac{1}{2}\)PD
⇒ PD = 2PB
Also, CD = CP + PD
= 2AP + 2PB = 2(AP + PB) = 2AB
CD = 2OO’ [∵ OABO’ is a rectangle]

Ch 10 Maths Class 9 Extra Questions Question 3.
ABCD is a parallelogram. The circle through A, B and C intersects (produce if necessary) at E. Prove that AE = AD.
Solution:

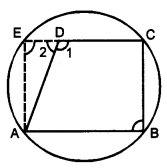
Given : ABCD is a parallelogram. Circle through A, B and C intersects CD produced in E.
To Prove: AE = AD
Proof : ABCE is a cyclic quadrilateral.
∴ ∠B + ∠E = 180° …(i)
ABCD is a parallelogram.
∴ ∠B = ∠1 … (ii)
Also, ∠1 + ∠2 = 180° [linear pair]
∠B + ∠2 = 180° …(iii) [using (ii)]
Now, from (i) and (iii), we have
∠B + ∠E = ∠B + ∠2
∠E = ∠2 In ∆DE, we have
∠E = ∠2
⇒ AD = AE [side opposite to equal angles of a A]

Circles Class 9 Questions With Solutions Question 4.
If two equal chords of a circle intersect within a circle, prove that the line segment joining the point of intersection to the centre makes equal angles with the chords.
Solution:

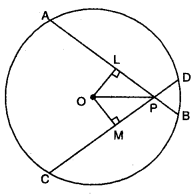
Join OP, draw OL ⊥ AB and OM ⊥ CD.
Thus, L and M are the mid-points of AB and CD respectively. Also, equal chords are equidistant from the centre.
∴ OL = OM
Now, in right-angled As OLP and OMP
OL = OM
OP = OP [common]
∠OLP = ∠OMP [each = 90°]
So, by RHS congruence axiom, we have
∆OLP ≅ ∆OMP
Hence, ∠OPL = ∠OPM [c.p.c.t.]

Class 9 Maths Ch 10 Extra Questions Question 5.
If two circles intersect in two points, prove that the line through their centres is the perpendicular bisector of the common chord.
Solution:

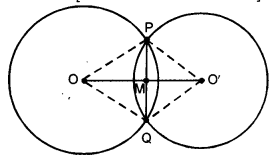
Given : Two circles Clo, r) and C(O’, s)intersect at P and Q.
To Prove : OO’ is perpendicular bisector of the chord PQ.
Const. : Join OP, OQ, O’P and O’Q
Proof : In ∆OPO’ and ∆OQO’
OP = OQ [radii of same circle]
OᏢ = QQ [radii of same circle]
OO’ = OO [common]
⇒ ∆OPO’ ≅ ∆OQO’ [by SSS congruence axiom]
⇒ ∠POM = ∠QOM [c.p.c.t.]
Now, in ∆POM and ∆QOM
OP = OQ
(radii of same circle]
∠POM = ∠OOM [proved above]
OM = OM [common]
∆POM ≅ ∆QOM [by SAS congruence axiom]
PM = QM and ∠PMO = ∠QMO [c.p.c.t.]
Also, ∠PMO+ ∠QMO = 180° [linear pair]
⇒ ∠PMO = ∠QMO = 90°
Hence, OO’ is the perpendicular bisector of the chord PQ.

Circles Class 9 Extra Questions Long Answer Type

Question 1.
In the given figure, O is the centre of a circle of radius r сm, OP and OQ are perpendiculars to AB and CD respectively and PQ = 1cm. If AB || CD, AB = 6cm and CD = 8cm, determine r.

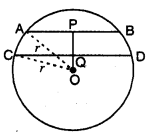
Solution:
Since the perpendicular drawn from the centre of the circle to a chord bisects the chord. Therefore, P and Q are mid-points of AB and CD respectively.
Consequently, AP = BP = \(\frac{1}{2}\)AB = 3 cm
and CQ = QD = \(\frac{1}{2}\)CD = 4 cm
In right-angled AQAP, we have
OA² = OP² + AP²
r² = OP² + 3²
r² = OP² + 9
In right-angled ∆OCQ, we have
OC² = OQ² + CQ²
r² = OQ² + 4²
p² = OQ² + 16 … (ii)
From (i) and (ii), we have
OP² + 9 = OQ² + 16
OP² – OQ² = 16 – 9
x² – (x – 1)² = 16 -9 [where OP = x and PQ = 1 cm given]
x² – y² – 1 + 2x = 7
2x = 7 + 1
x = 4
⇒ OP = 4 cm
From (i), we have
r² = (4)² + 9
r² = 16 + 9 = 25
r = 5 cm

Question 2.
In a circle of radius 5 cm, AB and AC are two chords such that AB = AC = 6 cm, as shown in the figure. Find the length of the chord BC.

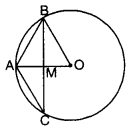
Solution:
Here, OA = OB = 5 cm [radii]
AB = AC = 6 cm
∴ B and C are equidistant from A.
∴ AO is the perpendicular bisector of chord BC and it intersect BC in M.
Now, in rt. ∠ed ∆AMB, M = 90° ….(i)
∴ By using Pythagoras Theorem, we have
BM² = AB² – AM²
= 36 – AM²
Also, in rt. ∠ed ∆BMO, ∠M = 90°
∴ By using Pythagoras Theorem, we have
BM² = BO² – MO² = 25 – (AO – AM)²
From (i) and (ii), we obtain
25 – (AO – AM)² = 36 – AM\(\frac{1}{2}\)
25 – AOC – AM² + 240 × AM = 36 – AM\(\frac{1}{2}\)
25 – 25 + 2 × 5 × AM = 36
10 AM = 36
AM = 3.6 cm
From (i), we have
BM² = 36 – (3.6)² = 36 – 12.96 = 23.04
BM = √23.04 = 4.8 cm
Thus, BC = 2 × BM
= 2 × 4.8 = 9.6 cm
Hence, the length of the chord BC is 9.6 cm.

Question 3.
In the given figure, AC is a diameter of the circle with centre O. Chord BD is perpendicular to AC. Write down the measures of angles a, b, c and d in terms of x.

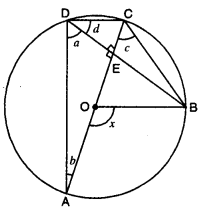
Solution:
Here, AC is a diameter of the circle.
∴ ∠ADC = 90°
⇒ ∠a + ∠d = 90°
In right-angled ∆AED, ∠E = 90°
∴ ∠a + 2b = 90°
From (i) and (ii), we obtain
∠b = ∠d ….(iii)
Also, ∠a = ∠c … (iv)
[∠s subtended by the same segment are equal]
Now, ∠AOB and ∠ADB are angles subtended by an arc AB at the centre and at the remaining part of the circle.

Question 4.
Show that the quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.

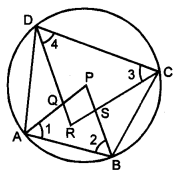
Solution:
Given : A cyclic quadrilateral ABCD in which AP, BP, CR and DR are the angle bisectors of ∠A, ∠B, 2C and ∠D respectively such that a quadrilateral PQRS is formed. To Prove: PQRS is a cyclic quadrilateral.
Proof : Since ABCD is a cyclic quadrilateral.
∴ ∠A + 2C = 180° and ∠B + ∠D = 180°
Also, AP, BP, CR and DR are the angle bisectors of ∠A, ∠B, ∠C and ∠D respectively.

or ∠1 + ∠3 = 90°
and ∠2 + ∠4 = 90°
Now, in ∆APB, by angle sum property of a ∆
∠1 + ∠2 + ∠P = 180° … (iii)
Again, in ∆CRD, by angle sum property of a ∆
∠3 + ∠4 + ∠R = 180° …(iv)
Adding (iii) and (iv), we have
∠1 + ∠2 + ∠3 + ∠4 + ∠P + ∠R = 180° + 180°
90° + 90° + ∠P + ∠R = 360° [using (ii)]
∠P + ∠R= 360° – 180° = 180°
i.e., the sum of one pair of the opposite angles of quadrilateral PQRS is 180°.
Hence, the quadrilateral PQRS is a cyclic quadrilateral.

Circles Class 9 Extra Questions HOTS

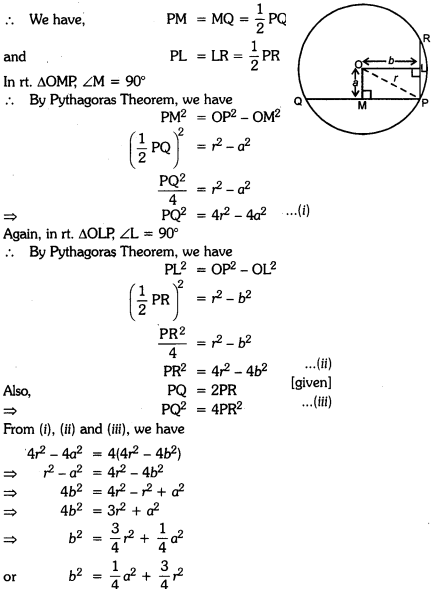
Question 1.
PQ and PR are the two chords of a circle of radius r. If the perpendiculars drawn from the centre of the circle to these chords are of lengths a and b, PQ = 2PR, then prove that:
\(b^{2}=\frac{a^{2}}{4}+\frac{3}{4} r^{2}\)
Solution:
In circle Clo, r), PQ and PR are two chords, draw OM I PQ, OL I PR, such that OM = a
and OL = b. Join OP. Since the perpendicular from the centre of the circle to the chord of the circle, bisects the chord.

Question 2.
Bisectors of angles A, B and C of triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the ∠DEF are 90° – \(\frac{\angle A}{2}\), 90° – \(\frac{\angle B}{2}\) and 90° – \(\frac{\angle C}{2}\) respectively.
Solution:

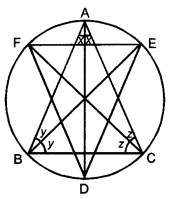
Let ∠BAD = x, ∠ABE = y
and ∠ACF = 2, then
∠CAD = x, ∠CBE = y
and ∠BCF = 2 [AD, BE and CF is bisector of ∠A, ∠B and ∠C]
In ∆BC,
∠A + ∠B + ∠C = 180°
⇒ 2x + 2y + 2Z = 180°
or x + y + Z = 90° …(i)
Now, ∠ADE = ∠ABE
and ∠ADF = ∠ACF [angles in the same segment of a circle]
⇒ ∠ADE = y and ∠ADF = Z
⇒ ∠ADE + ∠ADF = y + Z
or ∠D = y + Z …(ii)
From (i) and (ii), we have
x + 2D = 90°
⇒ ∠D = 90° – x

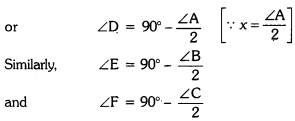
Circles Class 9 Extra Questions Value Based (VBQs)

Question 1.
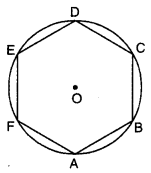
A small cottage industry employing people from a nearby slum area prepares round table cloths having six equal designs in the six segment formed by equal chords AB, BC, CD, DE, EF and FA. If O is the centre of round table cloth (see figure). Find ∠AOB, ∠AEB and ∠AFB. What value is depicted through this question ?

Solution:
Since six equal designs in the six segment formed by equal chords AB, BC, CD, DE, EF and FA.
Therefore, we have six equilateral triangles as shown in the figure. Since ∆AOB, ∆BOC, ∆COD, ∆DOE, ∆EOF
∴ Each angle is equal to 60°.

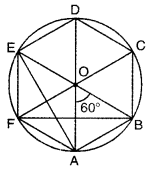
∠AOB = 60°
∠AOB, ∠AEB and ∠AFB are angles subtended by an arc AB at the FK centre and at the remaining part of the circle.
∴ ∠AEB = ∠AFB = \(\frac{1}{2}\) ∠AOB = \(\frac{1}{2}\) × 60° = 30°
Thus, ∠AEB = ∠AFB = 30°
Value depicted : By employing people from a slum area to prepare round table clothes reali∠e their social responsibility to work for helping the ones in need.

Question 2.
A circular park of radius 10 m is situated in a colony. Three students Ashok, Raman and Kanaihya are standing at equal distances on its circumference each having a toy telephone in his hands to talk each other about Honesty, Peace and Discipline.
(i) Find the length of the string of each phone.
(ii) Write the role of discipline in students’ life.
Solution:
(i) Let us assume A, B and C be the positions of three students Ashok, Raman and Kanaihya
respectively on the circumference of the circular park with centre O and radius 10 m. Since the centre of circle coincides with the centroid of the equilateral ∆ABC.

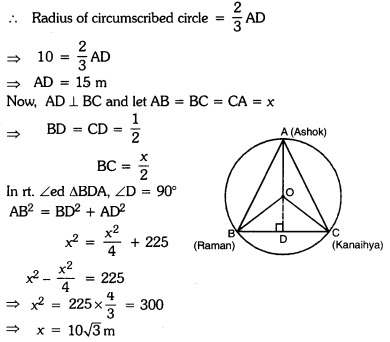
Thus, the length of each string is 10√3 m.
(ii) In students’ life, discipline is necessary. It motivates as well as nurture the students to make him a responsible citizen.