Structure of Atoms Class 11 Notes Chemistry Chapter 2

By going through these CBSE Class 11 Chemistry Notes Chapter 2 Structure of Atoms, students can recall all the concepts quickly.

Structure of Atoms Notes Class 11 Chemistry Chapter 2

Sub-Atomic Particles: Dalton’s Atomic Theory regarded the atom as the ultimate particle of matter. It explained satisfactorily various laws of chemical combination like the law of conservation of mass, the law of constant composition, and the law of multiple proportions. However, it failed to explain the existence of sub-atomic particles which were later discovered like electrons and proton.

Discovery of Electron: Michael Faraday suggested the particular nature of electricity. When he passed electricity through a solution of an electrolyte, chemical reactions occurred at the electrodes with liberation and deposition of matter at the electrodes.

Michael Faraday discovered the sub-atomic particles like electrons from his well-known experiments in partially evacuated glass tubes called cathode ray discharge tubes. The cathode ray tube is made of glass containing two thin pieces of metal, called electrodes, sealed in it.

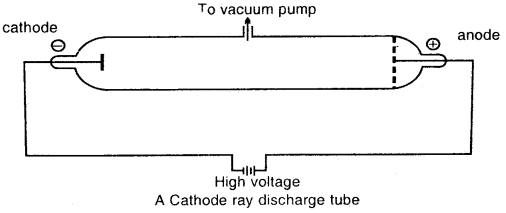
At very low pressure and at high voltage, current starts flowing through a stream of particles from cathode to anode. These were called cathode rays or cathode ray particles

Characteristics of Cathode rays:

1. The cathode rays start from the cathode and move towards the anode.
2. These rays travel in straight lines.
3. Cathode rays are made up of material particles.
4. On applying an electric field, these rays are deflected towards the positive plate. This shows that cathode rays carry a negative charge. These negatively charged particles are Electrons.
5. Cathode rays produce a heating effect.
6. They produce X-rays when they strike against the surface of hard metals like tungsten, molybdenum, etc.
7. They produce green fluorescence when they stride zinc sulfide.
8. They affect the photographic plates.
9. They possess a penetrating effect.
10. They possess the same charge/mass ratio.

\(\frac{\text { Charge }}{\text { Mass }}=\frac{e^{-}}{m}\) = 1.76 × 10⁸ coulombs/g Mass m
Charge = e^– = 1.60 × 10^-19 coulombs or 4.8 × 10^-10 esu

Thus the mass of electron m
= \(\frac{e}{e / m}=\frac{1.60 \times 10^{-19}}{1.76 \times 10^{8}}\)
= 9.11 × 10^-28 g
= 9.11 × 10^-31 kg
Thus, it is concluded that electrons are the basic constituent of all atoms.

The amount of deviation of the particles from their path in the presence of an electrical or magnetic field depends upon

• The magnitude of the negative charge on the particle, the greater the magnitude of the charge on the particle, the greater is the deflection.
• The mass of the particle-lighter the particle, the greater is the deflection.
• The strength of the electrical or magnetic field.

The deflection of electrons from their original path increases with the increase in the voltage or strength of the magnetic field.

Thus electron can be defined as the fundamental particle which carries one unit negative charge and has a mass nearly equal to \(\frac{1}{1837}\)th of that of the hydrogen atom.

Discovery of Protons and Newtons: Anode rays or Canal rays: If a perforated cathode is used in the discharge tube experiment, it is found that certain type of radiations also travels from anode to cathode.

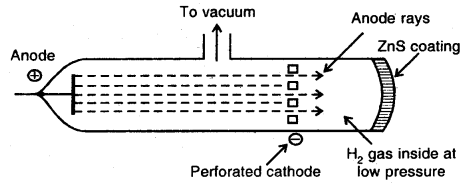
Production of Anode rays or Positive rays

Thus anode rays are not emitted from the anode but are produced in the space between the anode and cathode.

Properties of Positive rays/canal rays:

1. The anode-rays originate in the region between two electrodes in the discharge tube.
2. These rays are made of material particles.
3. These rays are positively charged.
4. These rays produce heat when striking against a surface.
5. The magnitude of the charge on anode-rays varies from particle to particle depending on the number of electrons lost by an atom or molecule.
6. The mass of positive particles which constitute these rays depend upon the nature of the gas in the tube.
7. The charge/mass (e/m) ratio of anode-rays is not constant but depends upon the nature of gas in the tube. The value of e/m is greatest for the lightest gas, hydrogen.

The electric charge on the lightest positively charged particle from hydrogen gas was found to be exactly equal in magnitude but opposite in sign to that of the electron. This lightest positively charged particle from hydrogen gas was named a proton. The mass of a proton is almost 1836 times that of the electron.

When hydrogen gas is taken inside the tube
Charge on these particles = 1.6 × 10^-19 coulomb
\(\frac{\text { Charge }}{\text { mass }}\) = 958 × 10⁴ coulombs/g for each particle
∴ mass on each particle = \(\frac{1.6 \times 10^{-19}}{9.58 \times 10^{4}}\) = 1.67 × 10^-24 g

This mass is nearly the same as that of hydrogen atom.

Therefore, a Proton may be defined as the fundamental particle which carries one unit positive charge and has a mass nearly equal to that of the hydrogen atom.

Chadwick in 1932 discovered the 3rd sub-atomic neutral particle and named it Neutron. He bombarded a thin sheet of beryllium by a-particles to discover neutrons. Neutron is a neutral particle carrying no charge and has a mass slightly greater than that of proton/

Thomson Model of Atom:
J.J. Thomson proposed that an atom is a sphere (radius approximately 10-10 m) of positive electricity and electrons are embedded into like the seeds of watermelon. An important figure of this model is that the mass of the atom is uniformly distributed over the atom.

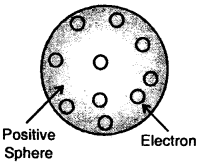
Thomson model of the atom

Later on, this model was rejected as Sphere electrons are mobile. Thomson model of the atom

Rutherford’s Nuclear Model of Atom: Rutherford bombarded very thin gold foil with a-particles.

The observations of this a-particle scattering experiment were:

1. Most of the a-particles passed through the gold foil undeflected.
2. A small fraction of the a-particles was deflected through small angles.
3. A very few a-particles (~ 1 in 20,000) bounced back, that is, were deflected by nearly 180°.

Conclusions:

1. Atom is hollow from within. There is empty space within the atom as most of the a-particles passed undeflected.
2. A few positively charged a-particles were deflected. These must have been deflected by some positively charged body present within the atom. This positively charged body is very small as compared to the size of the atom.
3. Calculations by Rutherford showed that the radius of this positive center called Nucleus is only 10^-15 m as compared to the radius of the atom which is about 10^-10 m.

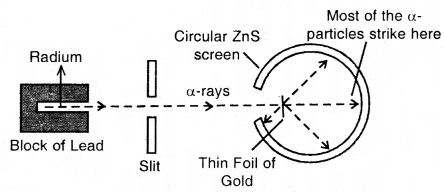
Rutherford’s scattering experiments

On the basis of the above observations and conclusion, Rutherford proposed the nuclear model of the atom.
1. The positive charge and most of the mass of the atom were densely concentrated in an extremely small region. This very small portion of the atom was called the nucleus by Rutherford.

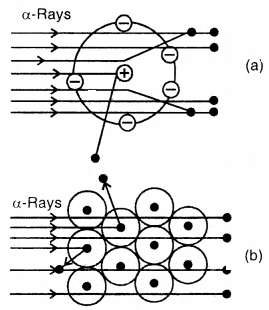
Scattering of a-particles by
(a) a single atom (b) a group of atoms

2. The nucleus is surrounded by electrons that move around the nucleus at a very high speed in circular paths called orbits. Thus, Rutherford’s model of the atom is similar to the solar system in which the nucleus is like the sun and moving electrons are like revolving planets.

3. Electrons and the nucleus are held together by electrostatic forces of attraction.

Atomic Number and Mass Number: Atomic Number (Z) is the number of protons present in the nucleus.
As an atom is electrically neutral, the no. of protons in the nucleus is equal to the number of electrons moving outside it.
No. of protons in hydrogen (Z) = 1
= no. of electrons in a neutral atom

No. of protons in sodium (Z) = 11
= no. of electrons in a neutral atom

While the positive charge of the nucleus is due to protons, the mass of the nucleus, due to both protons and neutrons. As both protons and neutrons are present in the nucleus, they are collectively called Nucleons.

The total no. of nucleons is termed as the Mass number (A) = No. of protons (Z) + No. of neutrons (n)
∴ No. of neutrons n = A – Z

→ Isobars and Isotopes: The composition of any atom of symbol, X can be represented by _Z^AX.

→ Isobars are defined as the atoms of different elements with the same mass number but a different atomic number, e.g., ₆¹⁴C and ₇¹⁴N

→ Isotopes are the atoms of the same element with the same atomic number but different mass numbers. Protium (₁¹H), deuterium (₁²D), and tritium (₁³T) are the isotopes of hydrogen.

Similarly, ₁₇³⁵Cl and ₁₇³⁷Cl are the isotopes of chlorine.

The chemical properties of atoms are controlled by the number of electrons which are determined by the no. of protons in the nucleus. No. of neutrons present in the nucleus have very little effect on the chemical properties of an element. Thus all the isotopes of a given element show the same chemical behavior.

→ Drawbacks of Rutherford Model of Atom:
1. According to Maxwell, charged particles when moving, dissipates energy in the form of electromagnetic radiations.
Slowly, the distance between the moving electron from the nucleus decreases. Calculations show that it should take an electron only 10^-8 to spiral into the nucleus.

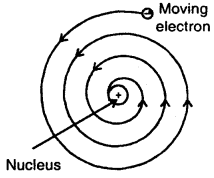
But this does not happen. Thus Rutherford’s model cannot explain the stability of an atom.

2. Another serious drawback of the Rutherford model is that it says nothing about the electronic structure of atoms, i.e., how the electrons are distributed around the nucleus and what are the energies of these electrons.

→ Developments leading to Bohr’s Model of Atom: Neils Bohr improved upon the model of the atom as proposed by Rutherford.

Two developments played a major role in the formulation of Bohr’s model of the atom.

1. Electromagnetic radiations possess both wave-like and particle-like properties.
2. Quantization of electronic energy levels in atoms.

→ Wave Nature of Electromagnetic Radiation: Maxwell was the first to suggest that charged bodies moving under acceleration, produce alternating electrical and magnetic fields. These fields are transmitted in the form of waves called electromagnetic waves or electromagnetic radiations.

Properties associated with electromagnetic wave motion:

1. Electric and magnetic fields are perpendicular to each other and both are perpendicular to the direction of propagation of the wave.
2. These waves do not require medium and can move in a vacuum.
3. There are many types of electromagnetic radiations that differ from one another in wavelength (or frequency). They constitute electromagnetic spectrum (shown below). A visible part of the spectrum (around 10¹⁵ Hz) is only a small part of it.
4. Different kinds of units are used to represent electromagnetic radiation.
   SI unit for frequency (v -nu) is hertz (Hz, s^-1).

It is defined as the number of waves that pass through a given point in space in one second.
SI unit for wavelength (λ) should be a meter.
(a) Wavelength (λ): It is the distance between two consecutive points which are in the same phase along the direction of propagation. Depending upon the magnitude, the wavelength is expressed either in cm, micron, millimicron, Angstrom unit, or in nanometer.
1 Angstrom (Å) = 10^-8 cm = 10^-10 m
1 micron (g) = 10^-4 cm = 10^-6 m.
1 nanometer = 10^-9 m

(b) Frequency (v): It is defined as the number of wavelengths travelled in one second. Therefore,
v = \(\frac{\text { Velocity of the radiation }}{\text { Wavelength of the radiation }}=\frac{c}{\lambda}\)

The frequency is expressed in cycles per second or in Hertz (Hz) units.
1 Hz = 1 cycle/s

(c) Wave number (\(\bar{v}\)): It is defined as the number of wavelengths which can be accommodated in one cm length along the direction of propagation. Therefore,
Wave number (\(\bar{v}\)) = \(\frac{\text { Frequency of the radiation }(v)}{\text { Velocity of the radiation }(c)}=\frac{v}{c}\)

The wave number is generally expressed in the units of cm^-1, although it is not the SI unit.
Frequency = Velocity × wave number
or
v = c\(\bar{v}\)

Relationship between velocity, wavelength, and frequency of wave:
c = V × λ
where c = velocity, v = frequency, λ = wavelength

Electromagnetic spectrum: The different types of electromagnetic radiations differ only in their wavelengths and have frequencies.

The wavelengths increase in the following order.
Cosmic rays < γ-rays < X-rays < Ultra-violet rays < Visible rays < Infrared < Microwaves < Radio waves

(a) The spectrum of electromagnetic radiation

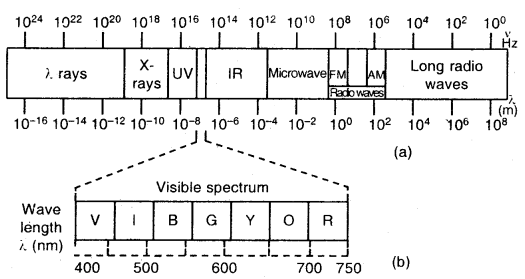
(b) Visible spectrum: The visible spectrum is onlv a small part of the entire spectrum

In a vacuum, all types of electromagnetic radiations, regardless of wavelength, travel at the same speed, i.e., 3.0 × 10⁸ ms^-1
This is called the speed of light and is given the symbol ‘c’.

Particle Nature of Electromagnetic Radiation: Planck’s Quantum Theory
The wave nature of electromagnetic radiation could explain experimental phenomena such as diffraction and interference. However, the experimental observations such as the emission of, radiation from a hot body, and the photoelectric effect could not be explained in terms of the wave nature of light.

→ Black body radiation: All hot bodies emit electromagnetic radiation. At high temperatures, a part of these radiations lies in the visible region of the spectrum With a further increase in the temperature of the body, the proportion of the higher frequency radiation increases. An ideal body that emits and absorbs radiations of all frequencies is called a black body.

Max Planck found that the characteristics of black body radiation could be accounted for by proposing that each electromagnetic oscillator, viz., an atom or a molecule, can emit or absorb only a certain discrete quantity of energy. This limitation of the energy of an object to discrete values is called the quantization of energy. According to Planck, the energy of an oscillator of frequency v is restricted to an integral multiple of the quantity, hv, where h is called the Planck’s constant.

→ Plank gave the name quantum to the smallest quantity of energy that can be emitted or absorbed in the form of electromagnetic radiation. The energy (E) of a quantum of radiation is proportional to its frequency (v) and is expressed as
E = h v

h is called Planck’s constant and has the value 6.626 × 10^-34 Js.
Thus, according to Planck
E = n h v
where n = 0,1, 2 , h = 6.626 × 10^-34 Js

The smallest amount of energy (n = 1) is then given by
E = h v

The energy to h v is called a quantum of energy that can be emitted or absorbed in the form of electromagnetic radiation.

→ The energy of Electromagnetic Radiation: All electromagnetic radiations are associated with a certain amount of energy.

According to Einstein

1.The radiation energy is emitted or absorbed in the form of small packets of energy. Each such packet of energy is called a quantum or photon. Each quantum has a certain discrete amount of energy associated with it.

2. Energy associated with a quantum or photon (e) is proportional to the frequency (v) of the radiation
Then E ∝ v
or
E = hv

where h is a constant called Planck’s constant. This constant (h) has value of 6.626 × 10^-34 Joule second (Js) or 3.99 × 10^-13 kJs mol^-1
The above relation may be written as ε = \(\frac{h c}{\lambda}\)

3. The energy associated with Avogadro’s number (N) of quanta is called an Einstein of energy (E). Thus, the Einstein of energy associated with the radiation of frequency v is. E = N_A hv

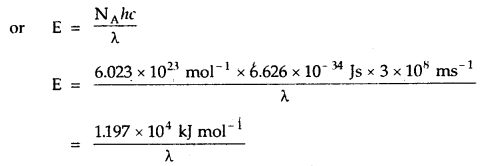
Photoelectric Effect: When a beam of light of suitable wavelength falls on a clean metal plate (such as cesium) in a vacuum, electrons are emitted from the surface of the metal plate. This phenomenon involving the emission of electrons from the surface of a metal by the action of light is known as the photoelectric effect. The electrons so emitted are called photoelectrons.

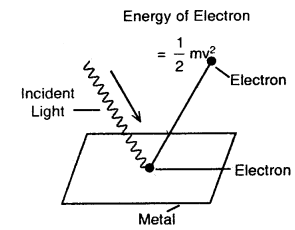
Photoelectric effect

The three important facts about the photo-electric effect observed are
1. The electrons are ejected only if the radiation striking the surface of the metal has at least a certain minimum frequency called threshold frequency (v_o). If the frequency is less than v_o, no electrons are ejected.
This value (v_o) is called Threshold Frequency. The minimum energy required to eject the electron (hv_o) is called the work function.

2. The velocity (and hence the kinetic energy) of the electron ejected depends upon the frequency of the incident radiation and is independent of its intensity.

3. The number of photoelectrons ejected is proportional to the intensity of incident radiation.

The above observations cannot be explained by the Electromagnetic wave theory. According to this theory, since radiations are continuous, therefore it should be possible to accumulate energy on the surface of the metal, irrespective of its frequency and thus radiations of all frequencies should be able to eject electrons.

Similarly, according to this theory, the energy of the electrons ejected should depend upon the lire intensity of the incident radiation.

If the striking photon of light has energy = hv and the minimum energy required to eject the electron is hv_o then the difference of energy (hv – hv_o) is transferred as the kinetic energy of the photoelectron
\(\frac{1}{2}\)hv – hv_o = h(v – v_o)

where m = mass of the electron and v is the velocity of the ejected electron.

Dual Behaviour of Electromagnetic Radiation: The particle nature of light can explain the black body radiation and photoelectric effect satisfactorily but cannot explain the known wave behavior of light like the phenomenon of interference and diffraction. Therefore, light possesses dual behavior either as a wave or as a stream of particles.

When radiation interacts with matter, it displays particle-like properties. When it propagates, it displays wave-like properties like diffraction and interference. Some microscopic particles like electrons also exhibit this wave-particle duality.

→ Evidence for the Quantized Electronic Energy Levels: Atomic Spectra: Atoms give discontinuous or line spectra. The spectrum given by atoms consists of a series of bright lines or bands separated from each other by a dark space. Each line in the spectrum corresponds to a specific wavelength.

There are two types of atomic spectra

1. Atomic emission spectra,
2. Atomic absorption spectra

1. Atomic emission spectra: A series of bright lines, separated from each other by dark spaces, produced by the excited atoms is called atomic emission spectra.

Each line in the emission spectrum corresponds to a specific wavelength. Therefore, each element gives a unique pattern of lines in the spectrum. No two elements give the same pattern of lines in their spectra.

2. Atomic absorption spectra: When a sample of atomic vapors is placed in the -path of white light from an arc lamp, it absorbs the light of certain characteristic wavelengths, and the light of other wavelengths gets transmitted. This produces a series of dark lines on a white background.

The spectrum of Hydrogen Atom: The spectrum of a hydrogen atom can be obtained by passing an electric discharge through the gas taken in the discharge tube under pressure. The spectrum consists of a large number of lines appearing in different regions of wavelengths. The lines in different regions were grouped into five different series of lines, each being named after the name of its discoverer.

These are the Lyman series. Balmer series, Paschen series, Brackett series and Pfund series. Lyman series appear in the ultraviolet region, Balmer series appear in the visible region while the other three series lie in the infrared region.

A simple relationship between the wavelengths of different lines can be given as
\(\frac{1}{λ}\) = \(\bar{v}\)(in cm^-1)
= R(\(\frac{1}{n_{2}^{2}}-\frac{1}{n_{1}^{2}}\))

where n₁ and n₂ are integers, such that n₁ > n₂. R is a constant, now called the Rydberg constant. The value of R is 109678 cm^-1. This expression is found to be valid for all the lines in the hydrogen spectrum and is also known as Rydberg equation.

For a given spectrum series, n₂ remains constant while n1 varies from line to line in the same series. For example, for Lyman series n₂ = 1 and = 2, 3, 4, 5 and for Balmer series n₂ = 2 and n₁ = 3, 4, 5

…. All the five series, the regions in which lines appear and the values of n₁ and n₂ are given below:


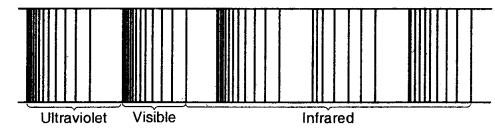
Emission or atomic spectrum of hydrogen

Of all the elements, the hydrogen atom has the simplest line spectrum.

Bohr’s Model For Hydrogen Atom Postulates:
1. The electron in the hydrogen atom can move around the. the nucleus in a circular path of fixed radius and energy. These paths are called orbits, stationary states, or allowed energy states.

2. The energy of an electron in the orbit does not change with time. However, it jumps from a lower energy level to a higher energy level where the requisite amount of energy is supplied to it and jumps from a higher orbit to a lower orbit with the release of energy.
ΔE = E₂ – E₁
where ΔE = change in energy, E₂ = energy of the electron in the higher orbit, E₁ = energy of the electron in the lower orbit.

3. The frequency of the radiation absorbed or emitted is given by
v = \(\frac{\Delta \mathrm{E}}{h}=\frac{\mathrm{E}_{2}-\mathrm{E}_{1}}{h}\)

4. The angular momentum of an electron in a given stationary state can be expressed as
mvr = \(\frac{n h}{2 \pi}\); n = 1, 2,3 2n
Thus an electron can move only in those orbits for which its angular momentum is an integral multiple of \(\frac{h}{2 \pi}\) (Quantization of angular momentum).
That is why only certain fixed orbits are allowed.

(a) The stationary states for electrons are numbered n = 1, 2, 3… . They are called Principal quantum numbers.
(b) the radii of stationary states are expressed as
r_n = n²a₀
where a_o = 52.9 pm

Thus the radius of the first orbit called Bohr radius is 52.9 pm (as n = 1).

(c) Energy of the electron in a given orbit
E_n = – R_H\(\left[\frac{1}{n^{2}}\right]\) where n = 1, 2, 3, ……….
R_H is called Rydberg Constant and its value is 2.18 × 10^-18 J. The energy of the lowest state, also called the ground state is
E₁ = – 2.18 × 10-18(\(\frac{1}{1^{2}}\)) = – 2.18 × 10^-18 J
For n = 2
E₂ = – 2.18 × 10-18(\(\frac{1}{2^{2}}\)) = – 0.545 × 10^-18 J

Significance of the negative sign before the electronic energy E_n: The energy of the electron in a hydrogen atom has a negative sign for all possible orbits. A free-electron at rest far away place from the nucleus has energy = 0, i.e., E_∞ = 0. As the electron gets closer to the nucleus (n decreases) En becomes larger in absolute value and more and more negative. Thus the most negative energy given by n = 1 corresponds to the most stable orbit.

(d) Bohr’s theory can also be applied to ions containing only one ‘ electron like hydrogen. For example He⁺, Li²⁺, Be³⁺ and so on. For them
E_n = – 2.18 × 10^-18(\(\frac{\mathrm{Z}^{2}}{n^{2}}\)) J and radii
r_n = \(\frac{52.9\left(n^{2}\right)}{Z}\) pm
where Z = atomic number. It has a value of 2, 3 for helium and lithium respectively.

(e) Magnitude of the velocity of the electron increases with the increase in nuclear charge and decreases with the increase’ of principal quantum numbers.

→ Explanation of Line Spectrum of Hydrogen: The energy difference between the two orbits is given by
ΔE = E_f – E_i
E_f, E_i energies in final and initial orbits
ΔE = \(\left(\frac{-\mathrm{R}_{\mathrm{H}}}{n_{f}^{2}}\right)-\left(\frac{\mathrm{R}_{\mathrm{H}}}{n_{i}^{2}}\right)\)

n_f, n_i are final and initial orbits

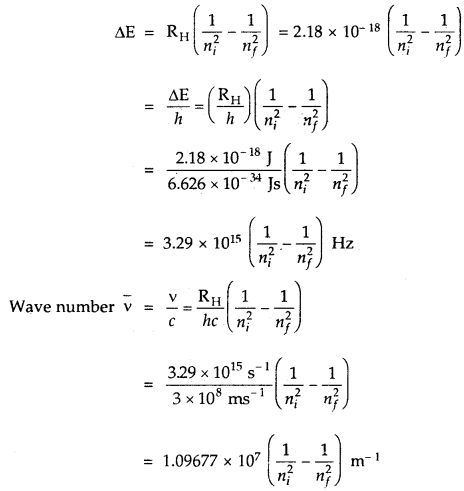
In the case of the absorption spectrum, n_f > n_i energy is absorbed.
In the case of emission spectrum n_i > n_f; ΔE is negative and energy is released.

Advantages of Bohr’s Model:

1. It explains the stability of the atom. An electron can not lose energy as long as it stays in a particular orbit.
2. It explains the line spectrum of hydrogen.

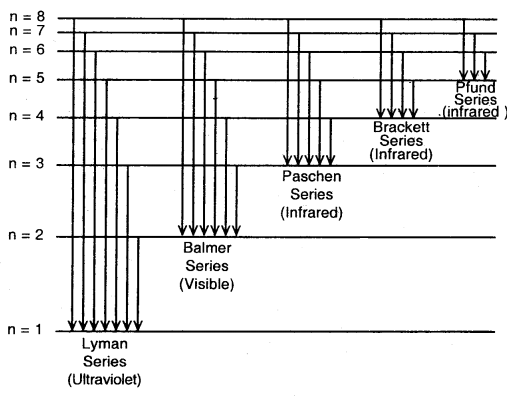
Different series in the hydrogen spectrum

Drawbacks of Bohr’s Model: Bohr’s model of atom suffers from the following weaknesses or limitations.
1. Inability to explain line spectra of multi-electron atoms: Bohr’s theory was successful in explaining the line spectra of the hydrogen atom and hydrogen-like particles, containing a single electron only. However, it failed to explain the line spectra of multi-electron atoms.

When spectroscopes with better resolving powers were used, it was found that even in the case of hydrogen spectrum, each line was split up into a number of closely spaced lines (called fine structure) which could not be explained by Bohr’s model of the atom.

2. Inability to explain Zeeman effect (splitting of lines in the magnetic field and stark effect (splitting of lines in the electric field)

3. Unable to explain the three-dimensional model of the atom. Bohr’s model gives a flat model of the atom with electrons moving in circular paths in one plane.

4. It does not explain the shapes of molecules.

5. It fails to explain de Broglie’s concept of the dual nature of matter and Heisenberg’s uncertainty principle.

Towards Quantum Mechanical Model of the Atom:
1. Dual Behaviour Matter: de-Broglie suggested that matter and hence electron-like radiations have a dual character – wave and particle. In other words, matter also possesses particles as well as Wave characters. This concept of the dual character of matter gave birth to the wave mechanical theory of matter according to which, the electrons, protons, and even atom when in motion possess all wave properties. Mathematically, de Broglie view may be written as below:
λ = \(\frac{h}{m v}\) …(1)

The equation (1) is known as de Broglie equation, m = mass of the particle, v = velocity of the particle, h = Planck’s constant, λ is the wavelength.

Since h is constant, its value is 6.6256 × 10^-34 Js
∴ λ ∝ \(\frac{1}{m v}\)
or
λ ∝ \(\frac{1}{\text { Momentum }}\)
(mv = momentum of a photon) … (2)

Equation (2) is known as de Broglie’s relationship which may be stated as the momentum of a particle in motion is inversely proportional to the wavelength of the waves associated with it.

2. Heisenberg’s Uncertainty Principle: One of the important consequences of the dual nature of an electron is the Uncertainty Principle, developed by Heisenberg. According to the Uncertainty Principle, it is impossible to determine simultaneously at any given moment both the position and momentum (velocity) of an electron with accuracy.

Mathematically, if Δx and Δp are the uncertainties in the position and momentum respectively, then
ΔxΔp ≥ \(\frac{h}{4 \pi}\)

One can see from this equation that if Ap increases, the Ax decreases and vice-versa. Since, Δp = m. Δv, hence the above equation can be written as
Δx × Δv >\(\frac{h}{4 \pi m}\)

Significance of Uncertainty Principle: One of the important implications of the Heisenburg Uncertainty Principle is that it rules out the existence of definite paths or trajectories of electrons and other similar particles.

The effect of the Heisenburg Uncertainty Principle is significant only for the motion of microscopic objects and is negligible for two macroscopic objects.

In dealing with milligram-sized or heavier objects, the value of Δv Δx is extremely small and insignificant and the associated uncertainties are hard of any real consequence. Therefore the precise statements of the position and momentum of electrons have to be replaced by the statements of probability, that the electron has at a given position and momentum. This is what happens in the quantum mechanical model of the atom.

→ Reasons for the failure of the Bohr Model: In the Bohr model, an electron is regarded as a charged particle moving in well-defined circular orbits about the nucleus. The wave character of the electron is not considered.

Bohr’s model of the hydrogen atom, therefore, not only ignores the dual behavior of matter but also contradicts Heisenburg’s Uncertainty Principle.

→ Quantum Mechanical Model of Atom: Quantum mechanics was developed independently by Heisenburg and Schrodinger.

Schrodinger equation is Ĥ φ = Eφ where Ĥ is a mathematical operator called Hamiltonian, E is the total energy of the system and φ is the wave function.

Important features of the quantum mechanical model of the atom:

1. The energy of the electrons in atoms is quantized.
2. The existence of quantized electronic energy levels is allowed solutions of the Schrodinger Wave Equation.
3. Both the exact position and exact velocity of an electron in an atom cannot be determined simultaneously. Therefore, only the probability of finding an electron at different points is required.
4. An atomic orbital is the wave function \p for an electron in an atom.
5. The probability of finding an electron at a point within an atom is proportional to the square of the orbital wave function, i.e., |φ|2 at that point. |φ|2 is called probability density and is always positive. From the value of | \p |2 at different points within an atom it is possible to predict the region around the nucleus where the electron will most likely be found.

Orbitals and Quantum Numbers:
→ Atomic Orbital: it is defined as the 3-dimensional region of space around the nucleus where the probability of finding an electron is maximum.

→ Quantum Numbers: The state of an electron in an atom is described by its location with respect to the nucleus and by its energy. Thus, the energy and angular momentum of an electron is quantized, i.e., an electron in an atom can have only certain permissible values of energy and angular momentum. These permissible states of an electron in an atom called Orbitals are identified by a set of four numbers. These numbers are called Quantum Numbers.

The various quantum numbers are
(a) Principal quantum numbers are denoted by n.
(b) Azimuthal or angular momentum quantum number denoted by l.
(c) Magnetic quantum number denoted by m.
(d) Spin quantum number denoted by s.

(a) Principal quantum number (n): This quantum number determines the main energy level or shell in which the electron in an atom is present and also the energy associated with it. In addition, it also determines the average distance of the electron from the nucleus in a particular shell. Starting from the nucleus, the energy shells are denoted as K, L, M, N, … etc., or as 1, 2, 3, 4, … etc: The maximum number of electrons that a shell can accommodate is 2n². Thus, K-shell (n = 1) can have a maximum of two electrons. L- shell (n = 2) can have eight electrons and similarly, eighteen electrons can be accommodated in M-shell (n = 3).

(b) Azimuthal or subsidiary or angular quantum number (l): This, the quantum number determines the angular momentum of the electron. This is denoted by l. The values of l give principal energy- shell in which an electron belongs. It can have positive integer values from zero to (n – 1) where n is the principal quantum number.
That is l = 0, 1,2, 3, …. (n – 1).

(c) Magnetic quantum number: This quantum number describes the behavior of an electron in a magnetic field. The values of ‘m’ are linked to that of l. For a given value of l, the possible values of m vary from -l to 0 and 0 to + l. Thus, the total values of m are (2l + 1). The orbitals are also named after the sub-shell in which these are present. The number of orbitals in different sub-shells are given:

(d) Spin quantum number: This quantum number describes the spin orientation of the .electron. It is designated by ‘s’. Since the electron can spin in only two ways-clockwise or anti-clockwise and, therefore, the spin quantum number can take only two values: + 1/2 or – 1/2. These two values are normally represented by two arrows pointing in the opposite direction i.e.↑ and ↓.

Shapes of atomic orbitals:
1. Shapes of s-orbitals: For s-orbitals, l = 0, hence the orbital angular momentum of an s-orbital is zero. As a result, the distribution of electron density is symmetrical around the nucleus and the probability of finding an electron for a given distance is the same at all angles. As the distribution of electron density is symmetrical, therefore, the most suitable figure to represent an s-orbital is a sphere.

(a) The probability of finding an electron is maximum near the nucleus and decreases with distance. In the case of 2s electrons, the probability is again maximum near the nucleus and then decreases to zero and increases again and then decreases as the distance from the nucleus increases. The intermediate region (a spherical shell) where the probability of finding an electron cloud is zero is called a Nodal surface/node. In general, any n orbital has (n – 1) nodes.

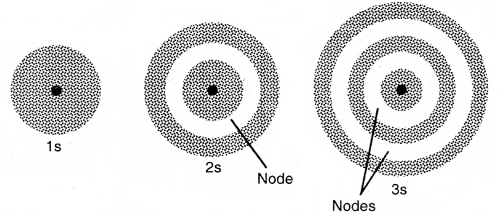
Shapes of is, 2s, and 3s orbitals

(b) The size and energy of the s-orbital increases as the principal quantum number n increases, i.e., size and energy of s-orbital increases in the order 1s < 2s < 3s ……

2. Shape of p-orbitals: For p-orbitals l = 1, so angular momentum of an electron in 2p orbital
= \(\sqrt{l(l+1)} \frac{h}{2 \pi}=\sqrt{2} \frac{h}{2 \pi}\)

As a result, the distribution of electron density around the nucleus is. not spherical. The probability diagram for a p-orbital is dumbbell shape. Such a diagram consists of a distorted sphere of high probability one on each side of the nucleus, concentrated along with N in a particular direction.

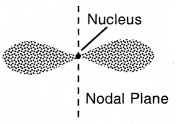
Shapes of p-orbital

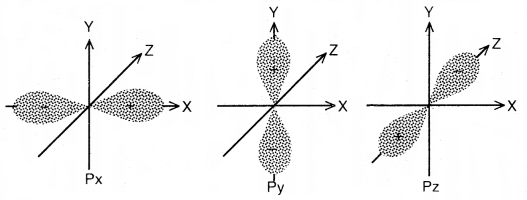
Different orientatios of p-orbitais

Now, since the electron with l = 1 can have three values for the magnetic quantum number (m), i.e., m = – 1, 0 and + 1, hence there are three p-orbitals. All three 2p-orbitals have the same shape, but their directions are different. The directions are perpendicular to each other. Since these directions can be chosen as the x, y, z axes, hence the p-orbitals along these axes are labeled as p_x, p_y, and p_z respectively. The three p-orbitals of a particular energy level have equal energies and are called degenerate orbitals. 2p has no node, 3p has one 4p has two nodes, and so on. In general, no. of nodes in any orbital = (n – l – 1).

3. Shape of d-orbitals: For d-orbital, 1 = 2. Therefore, the angular momentum of -an electron in d orbitals is not zero. As a result, the d orbitals do not show spherical symmetry. For l = 2, the magnetic quantum number (m) should have five different values i.e., m = – 2, – 1, 0, 1, + 2. Accordingly, there are five different space orientations for d orbitals. These are designated as

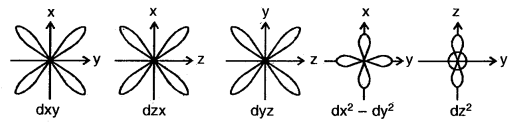
The five d-orbitals

4. Energies of orbitals: In atoms, electrons can have only certain permissible energies. These permissible states of electrons are called energy levels.

In hydrogen and hydrogen-like atoms, all the orbitals having the same principal quantum number have the same energy. Thus, 2s and 2p orbitals have equal energies, 3s, 3p, and orbitals have equal energies, and 4s, 4p, and 4f orbitals have equal energies as shown above.

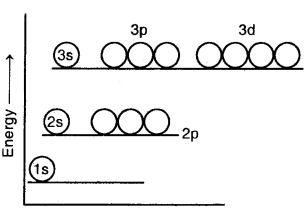
Energy level diagram for the few electronic shells of the hydrogen atom

The atoms containing two or more electrons are called multielectron atoms. In these atoms:
(a) Different orbitals having the same principal quantum number (n) may have different energies.
(b) For a particular main energy level, the orbital having a higher value of the azimuthal quantum number (l) has higher energy. For example, the energy of 2p orbital (l = 1) is higher than that of the 2s (l = 0) orbital, general, energies of the orbitals belonging to the same main energy level follow the order
s < p < d < f

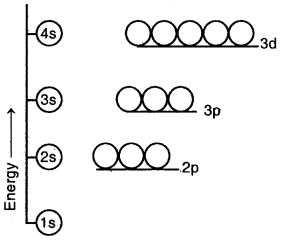
Energy level diagram for the few electronic shells of a multi-electron atom

(c) When n > 3, the same orbitals belonging to a lower main energy level may have higher energy than some orbitals belonging to the higher main energy. For example, in the case of multi-electron atoms, the energy of 3d orbitals is higher than the energy of 4s orbitals.

(d) In multielectron atoms, the energy of any orbital is governed by both the principal quantum number (n) and azimuthal quantum number (l):

• The orbital having leaver (n + l) value has lower energy.
• For the orbitals having equal value of (n + 1), the orbital having lower value of n has lower energy. For example.
  4s orbital has n + l = 4 + 0 = 4 and
  3d orbital has n + l = 3 + 2 = 5.

Since, (n + l) value for 4s orbital is lower than that for 3d, hence 4s orbital has lower energy than 3d.

5. Filling of orbitals in atoms:
Aufbau principle: In the ground state of the atoms, the orbitals are filled in order of their increasing energies. In other words, electrons first occupy the lowest-energy orbital available to them and enter into higher energy orbitals only after the lower energy orbitals are filled.

The order in which the energies of the orbitals increase and hence the order in which orbitals are filled is as follows:
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s …….

“n + l” Rule: The lower the value of (n + l) for an orbital, the lower is its energy, and hence earlier it will be filled. If two orbitals have the same value of (n + l), the orbital with the lower value of n will have lower energy. Hence it will be filled first.

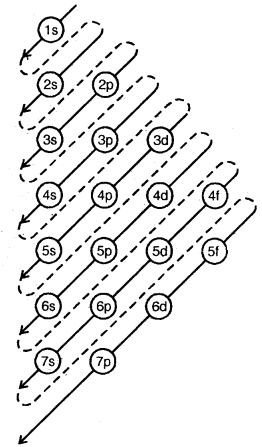
Order of Filling Energy Levels (Aufbau Principle)

→ Pauli Exclusion Principle
No two electrons in an atom can have the same set of four quantum numbers.
OR
Only two electrons may exist in the same orbital and these electrons must have opposite spin.

Hund’s rule of maximum multiplicity: According to this rule, electron pairing will not take place in orbitals of the same energy (same subshell) until each orbital is singly filled. This principle is very (important in guiding the filling of p, d, and f orbitals, which have more than one kind of orbitals. For example, we know that there are three p orbitals. (p_x, p_y, and p_z) of the p-subshell in a principal energy level. According-” to Hund’s rule, each o.f the three p orbitals must get one electron of parallel spin before any one of them receives the second electron of opposite spin.

The electronic configuration of some atoms are given below:

After calcium, 3d subshell starts getting filled. The electronic configurations of elements from scandium (Z = 21) to zinc (Z = 30) are given below:

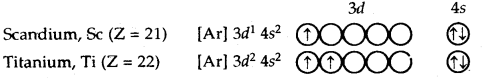
Total number of exchanges = 3+ 2 + l= 6
The number of exchanges that can take place in d5 configuration is as follows:

Gallium (Ga) Z = 31 to Krypton (Kr) Z = 36 (Electronic Configuration)
With Gallium (Ga) onwards, 4p orbitals get filled up as:

Important points to remember:

1. Mass No. (A) = Sum of protons and neutrons.
2. Atomic No. (Z) = No. of protons in the nucleus.
3. No. of neutrons = A – Z.
4. Nucleons are the particles (n + p) present in the nucleus.
5. Max. No. of electrons in a shell that can be present in an atom is given by 2n² where n = no. of the orbit.
6. An s-subshell can contain 2, a p-can contains 6, a d-can contain 10, and an f-subshell can contain 14 electrons, s-subshell has only one orbital; p-can has 3, d has 5; subshell has 7 orbitals.
7. Each orbital can maximum contains two electrons.
8. To form a cation from a neutral atom, electrons are removed equal to the no. of positive charges on the cation, while to form an anion from a neutral atom, electrons are added to the no. of negative charges on an anion.

Table Electronic Configurations of the Elements:

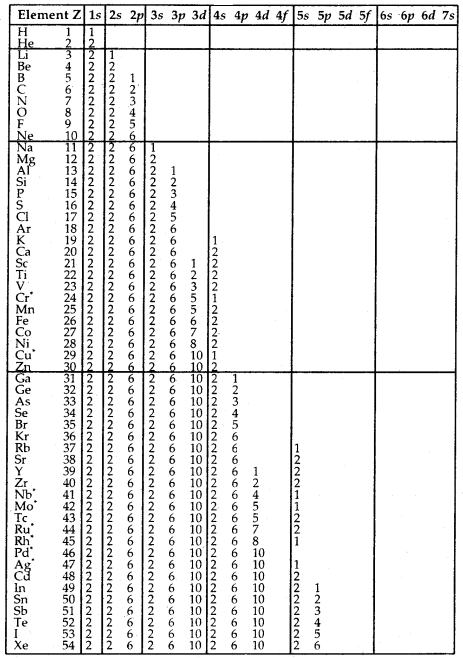
Elements with exceptional electronic configurations


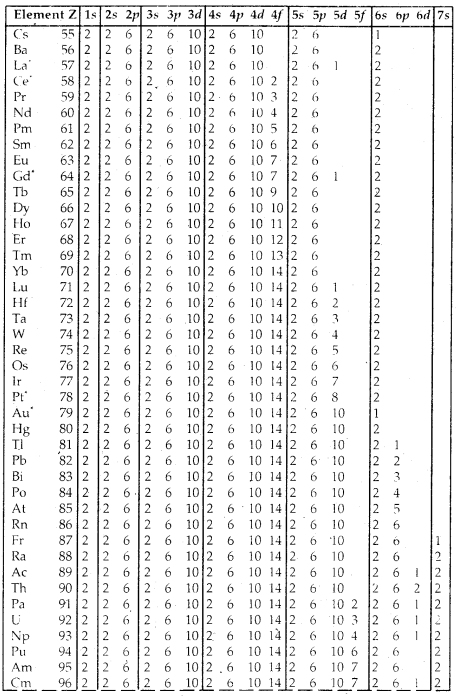
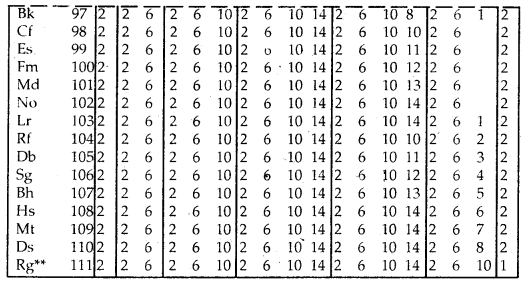
Elements with exceptional electronic configurations.

→ Elements with atomic number 112 amid above have been reported but not yet frilly a the indicated and min med.

→ Electron: It is the fundamental particle that carries one unit negative charge and has a mass nearly equal to \(\frac{1}{1837}\) hydrogen atom.

→ Proton: A proton may be defined as that fundamental particle that carries one unit of positive charge and has a mass nearly equal to that of the hydrogen atom.

→ Neutron: A neutron may be defined as the fundamental particle which carries no charge but has a mass nearly equal to that of a hydrogen atom or proton.

→ Cathode rays: Cathode rays are a stream of electrons.

→ Electrons: Electrons are universal constituents of matter.

→ Mass Number (A): Sum of protons and neutrons.

→ Atomic Number (Z): Number of protons in the nucleus of an atom.

→ Nucleons: Sum of protons and neutrons.

→ Isotopes: Atoms of the same element having the same atomic number, but different mass numbers are called Isotopes.

→ Isobars: Atoms of different elements which have the same mass number, but a different atomic number are Isobars.

→ Isotones: Such atoms of different elements which contain the same number of neutrons are called Isotones.

The wavelength (λ) of a wave is the distance between any two consecutive crests or troughs.
1 Å = 10^-8 cm = 10^-10 m
1 nm = 10^-9 m, 1 pm = 10^-12 m

→ Frequency (v): It is the number of waves passing through a point in space in one second. Its unit is Hertz (Hz).
1 Hz = 1 cycle per second (cps)

→ Velocity (c): The velocity of a wave is defined as the linear distance traveled by the wave in one second. Its unit is cm per second or meters per second.

→ Amplitude (a): It is the height of the crest or depth of the trough of a wave It is expressed in units of length.

→ Wavenumber: It is defined as the number of waves present in one cm length. It is also defined as the reciprocal of the wavelength
\(\bar{v}\) = \(\frac{1}{λ}\)

Relationship between velocity, wavelength, and frequency of a wave
c = v × λ

→ Electromagnetic spectrum: When electromagnetic radiations of different wavelengths are arranged in order of their increasing wavelengths or decreasing frequencies, the complete spectrum obtained is called Electromagnetic Spectrum,

Cosmic rays < y-rays < X-rays < UV rays < visible < Infrared < Microwaves < radiowaves

→ Photon: Each packet of energy is called quantum. In the case of light, such a quantum is called Photon.

→ Black Body Radiation: If the substance being heated is a black body (which is a perfect absorber and perfect radiator of energy) the radiation emitted is called blackbody radiation.

→ Zeeman Effect: Splitting of spectral lines in the magnetic field.

→ Stark Effect: Splitting of spectral lines in the electric field.

→ Probability.: It is the best possible description of a situation that cannot be exactly described.

→ Orbit: It, is a well-defined circular path around the nucleus with . a fixed energy in which the electrons revolve.

→ Orbital: The three-dimensional region of space around the nucleus where there is a maximum probability of finding an electron.

→ Quantum Numbers may be defined as a set of four numbers that give complete information about the electron in an atom, i.e., energy, orbital occupied, size, shape, and orientation of that orbital, and the direction of electron spin.

Some Important Formulae:
→ c = v × λ
c = velocity;
λ = wavelength,
v = Frequency

→ E = hv
h = Planck’s coristt. = 6.625 × 10^-34 J sec
E = Energy of a photon

→ \(\bar{v}\) = \(\frac{1}{λ}\)
\(\bar{v}\) = wavenumber .
Charge on 1 electron = – 1
Change on 1 proton = 1 +
Charge on 1 neutron = 0
Mass of one electron = 9.1 × 10^-31 kg
Mass of a proton = 1.67 × 10^-27 kg .
Mass of neutron = 1.67 × 10^-27 kg
One unit charge = 4.8 × 10^-10 e.s.u.
= 1.6 × 10^-19 coulomb

Work of R.A. Millikan ,
Charge on one electron = 1.6 × 10^-19 coulomb
e/m for electron = 1.76 × 10⁸

∴ Mass of an electron = \(\frac{e}{e / m}=\frac{1.60 \times 10^{-19}}{1.76 \times 10^{8}}\)
= 9.11 × 10^-28 g

If X is an atom of an element

Mass of 1 Mole of electron
. = 9.11 × 10^-28 × 6.022 × 10²³ g = 0.55 mg

→ Photoelectric Effect: The phenomenon of the emission of electrons from the surface of certain metals (usually potassium, cesium, rubidium). When they are exposed to a team of light with certain minimum frequency called threshold frequency.
hv = hv₀ + \(\frac{1}{2}\) mv²

K.E. imparted to the ejected electron .
= \(\frac{1}{2}\) mv² = hv – hv₀

→ Line spectrum of hydrogen
\(\bar{v}\) = 109677(\(\frac{1}{2^{2}}-\frac{1}{n^{2}}\)) cm^-1
where n > 3, i.e. n = 3, 4, 5, ….
The value 109677 cm-1 is called Rydburg Constant.

→ de Broglie Equation
λ = \(\frac{h}{m \times v}=\frac{h}{p}\)
where p = momentum of the particle.

→ Heisenburg’s Uncertainty Principle

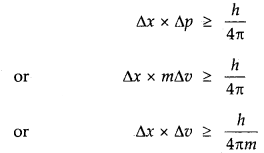
It is impossible to determine simultaneously both the position as well as momentum (or velocity) of a moving particle like an electron with absolute accuracy.

→ Pauli Exclusion Principle: No two electrons in an atom can have the same set of four quantum numbers.
Or
Only two electrons may exist in the same orbital and these electrons must have opposite spin.

→ The maximum number of electrons in the shell with principal quantum number n is equal to 2n².

→ Hund’s Rule of Maximum Multiplicity: Pairing of electrons in the orbitals belonging to the same subshell (p, d, or f) does not take place until each orbital belonging to that subshell has got one electron each, i.e., it is singly occupied.

→ Schrodinger Wave Equation: It is applicable to the wave nature of electrons.
Ĥ φ = E φ
where Ĥ is a mathematical operator called Hamiltonian operator.
or
\(\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{\partial^{2} \psi}{\partial y^{2}}+\frac{\partial^{2} \psi}{\partial z^{2}}+\frac{8 \pi^{2} m}{h^{2}}\)(E – V)φ = 0

where φ is the amplitude of the wave, x, y, z are space coordinates E is the total energy of the electron, V is its potential energy m is the mass of the electron.