By going through these CBSE Class 11 Chemistry Notes Chapter 6 Thermodynamics, students can recall all the concepts quickly.
Thermodynamics Notes Class 11 Chemistry Chapter 6
Thermodynamic Terms: The laws of thermodynamics deal with energy changes at a macroscopic system involving a large number of molecules rather than a microscopic system containing a few molecules
→ System: The part of the universe which is under thermodynamic study/scrutiny is called a system.
→ Surroundings: The remaining part of the universe with which the system can exchange both matter and energy is called the surrounding. System and surrounding taken together constitute the universe.
The universe = The system + the surroundings.
Types of System
1. Open System: An open system is one in which there is an exchange of matter and energy between the system and surroundings, e.g., a reaction occurring in a test tube.
2. Closed System: A closed system is one in which there is only a transfer of energy and not matter with the surroundings, e.g., the presence of reactants in a closed vessel.
3. Isolated System: An isolated system is one in which no exchange of energy and matter is possible between the system and the surroundings. The presence of reactants in a thermos flask is an example of an isolated system.
→ The State of the System: When the properties of a system like its pressure, volume, temperature, and composition are specified quantitatively, it is said to have stated. If any of these observable (measurable) properties undergo a change, the system is said to have another state.
→ State Variables: Such properties of the system, by changing any one of which, the system changes its state, are called State Variables.
→ State Function: A physical quantity is said to be a state function if its value depends upon the initial state and final state of the system and not the path followed by the system. Internal energy, enthalpy, free energy, entropy are all state functions. Heat and work are not state functions, because they depend upon the path followed.
→ Extensive Properties: Extensive properties of a system are those properties that depend upon the amount of substance contained in the system. Mass, volume, heat capacity, internal energy, enthalpy, Gibbs free energy are all extensive properties.
→ Intensive Properties: Intensive properties of a system are those which are independent of the quantity of matter contained in the system. They depend upon only the nature of the substance. Temperature, pressure, viscosity, density, surface tension, refractive index, specific heat, freezing point, boiling point are all intensive properties.
There are four types of thermodynamic processes:
- Isothermal Process: A process in which temperature remains constant.
- Adiabatic Process: A process in which no heat exchange takes place,(i.e., q = 0) between the system and surroundings.
- Isochoric Process: A process in which volume remains constant.
- Isobaric Process: A process in which pressure remains constant.
→ Internal Energy ‘U’: Its absolute value cannot be determined.
The energy stored within a substance (or system) is called its internal energy. It is a state function.
ΔU denotes a change in internal energy.
ΔU = U2 – U1 = Up – Ur
The internal energy of an ideal gas depends upon only its temperature.
Hence in an isothermal process involving an ideal gas ΔU = 0.
→ Reversible Process: When a process is carried out infinitesimally slowly so that it can be retraced at each step of the change, it is called a reversible process. In such a process system and surroundings are always in equilibrium. .
→ Irreversible Process: A process that is carried out so rapidly that the system does not get a chance to attain equilibrium It cannot be retracted to each step of the change. A reversible process may take infinite time for completion, whereas an irreversible process takes a finite time for completion.
- If wreversible = work obtained in a reversible process
- If wirreversible = work obtained in a reversible process is maximum.
→ Cyclic process: If a system after having undergone a series of changes returns back to its initial state, the process is called a cyclic process. The path of such a process is called a cycle.
In cyclic process ΔU = 0.
→ The first law of thermodynamics: States: “Energy can neither be created nor destroyed. However, it can be transformed from one form into another.”
In other words, the first law of thermodynamics can be stated as
“The total energy of the universe (system + surroundings) remains constant”.
The mathematical formulation of the first law of thermodynamics: Let us consider a system in its initial state having internal energy. U1 If heat equal to q is supplied to the system, and work equal to w is done on the system, then the internal energy of the system is the final state (U2) is given by
U2 = U1 + q + w
U2 – U1 = q + w
ΔU = q + w
or change in internal energy = Heat given to the system + work done on the syštem.
This relationship between internal energy, work, and heat is the mathematical statement of the first law of thermodynamics.
Applications: Heat, Work, and Internal Energy:
(a) Heat: The energy exchange between a system ad the surroundings when their temperatures are different is commonly known as heat.
If a system is at a temperature higher than the temperature of its surroundings, then it loses temperatures are different is commonly known as heat.
If a system is at a temperature higher than the temperature of its surroundings, then it loses heat energy to the surroundings. This transfer of heat lowers the temperature of the system and raises the temperature of the surroundings
(b) Work (w): Work is said to be done if the point of application of a force moves through a certain distance. For example, if a gas, enclosed in a cylinder fitted with an airtight piston has higher pressure than the external pressure, then the piston will move outwards. The piston continues to move until the pressure inside and outside are equal. In this, the gas inside the cylinder is pushing the piston outwards. Thus, the gas (system) is doing work.
(c) Internal Energy: the total energy contained in a system is called its internal energy or intrinsic energy. This is denoted by a symbol E or U.
The internal energy of a system depends upon the state of the system and not upon how the system attains that state. The internal energy thus is a state function.
Each substance or system possesses a definite amount of internal energy under a given set of conditions. For example, the internal energy of a system in state A be UA and in state B, it is UB. Then, change in the internal energy (ΔU) of the system is going from state A to B is
ΔU = Ufinal – Uinitial = UB – UA = wad.
wad is positive when work is done on the system. wad is negative if the work is done by the system.
This change in the internal energy depends only upon the initial and the final state and not on how this change is brought about.
Heat capacity and specific heat capacity:
1. Heat capacity: The heat capacity (C) of a sample of a substance is defined as the quantity of heat energy required to raise its temperature by 1 K (or 1°C). From this definition, we can write
Q = C. Δt
where Q is the quantity of heat given to the sample, At is the rise in the temperature of the substance. The unit of heat capacity is Joules per degree Celsius (J/°C or J°C-1) or Joules per Kelvin (J/K or JK-1).
2. Specific heat capacity: The specific heat capacity of a substance is equal to the quantity of heat required to raise the temperature of 1 unit mass of capacity of the substance by 1 °C, or 1 K.
S.I. unit of specific heat is joules per kilogram per degree (J/Kg°CorJ/kg.K).
3. Molar heat capacity: The molar heat capacity (cm) of a substance is defined as the quantity of heat required to raise the temperature of one mole of a substance by 1 K or (or 1°C). Thus
Molar heat capacity = Specific heat capacity × Molar mass
cm = C × M
The unit of molar heat capacity is J mol-1 K-1.
There are two types of Heat Capacities.
1. Heat capacity at a constant volume (Cv): The heat supplied to a system to raise its temperature through 1°C keeping the volume of the system constant is called heat capacity at constant volume.
2. Heat capacity at constant pressure (Cp): The heat supplied to a system to raise its temperature through 1°C keeping external pressure constant is called heat capacity at constant pressure.
Cv = \(\frac{d \mathrm{E}}{d \mathrm{~T}}\)
Cp = \(\frac{d \mathrm{H}}{d \mathrm{~T}}\)
Relationship between (Cp) and (Cv) Cp – Cv = R
→ Enthalpy (H): The sum of internal energy (E) and the product of pressure and volume is called enthalpy.
H = E + PV
P = Pressure,
V = Volume like E, Enthalpy is also a state function.
Its absolute value like E cannot be determined.
Nor is there any necessity for it. What is required is ΔH:
Change in enthalpy.
The value of ΔE and ΔH can be measured with the help of a Bomb Calorimeter. Calorimetry is the technique to measure energy changes associated with chemical or physical processes.
ΔH = Hproducts – Hreactants
The enthalpy change of a reaction: (ΔrH) is equal to the heat absorbed or evolved during a reaction at constant temperature and pressure.
∴ ΔH = qp where qp: Heat absorbed or evolved at constant pressure.
ΔH = ΔE + P ΔV … (1)
When there is no change in volume (i.e. ΔV = 0)
ΔE = qv where qv = Heat change at constant volume.
Equation (1) becomes
qP = qv + PΔV
qP = qv + ΔngRT
where Δng is the change in the no. of gaseous moles of the products minus that of the reactants.
Sign Convention for Heat and Work
- Heat absorbed by the system = q positive
- The heat evolved by the system = q negative
- Work done on the system = w positive
- Work done by the system = w negative
Enthalpies or Heats of Reactions (ΔrH):
The enthalpy change (amount of heat evolved or absorbed) during a chemical reaction, the moles of reactants and products being the same as indicated by the balanced chemical equation is called Enthalpy of the reaction (ΔrH).
Exothermic Reaction: These are the reactions in which heat is evolved. Here sum of heat contents of the reactants (HR) > Sum of heat contents of the products (Hp).
or
HR > Hp .
or
ΔH = Hp – HR < 0
or
ΔH < 0
or
ΔH is negative
Examples of exothermic reactions:
- C(s) + O2(g) → CO2(g) + 393.5 kJ
- H2(g) + \(\frac{1}{2}\)O2(g) → H2O(1) + 285.8 kJ
- N2(g) + 3H2(g) → 2NH3(g) + 92.4 kJ
or in terms of ΔH
- C(s) + O2(g) → CO2(g); ΔH = – 393.5 kJ
- H2(g) + \(\frac{1}{2}\)O2(g) → H2O(l); ΔH = – 285.8 kJ
- N2(g) + 3H2(g) → 2NH3(g); ΔH = – 92.4 kJ
→ Endothermic Reactions: These reactions which proceed with an absorption of heat are called endothermic reactions.
In endothermic reactions sum of the enthalpies of the product > Sum of the enthalpies of reactants
or
ΣHp > ΣHR
or
ΔH = Hp – HR > 0
or
ΔH >0
or
ΔH is positive
Examples of endothermic reactions
- N2(g) + O2(g) → 2NO(g) – 180.7 kJ
- C(s) + H2O(g) → CO(g) + H2(g) – 131.4 kJ
- C(s) + 2S → CS2(g) – 92.4 kJ
or writing the above thermochemical equation in terms of AH
- N2(g) + O2(g) → 2NO(g); ΔH = + 180.7 kJ
- C(s) + H2O(g) → CO(g) + H2(g); ΔH = + 131.4 kJ
- C(s) + 2S → CS2(g); ΔH = + 92.4 kJ
→ Thermochemical Equation: When a balanced chemical equation not only indicates the quantities of different reactants and products but also indicates the amount of heat evolved or absorbed, it is called a thermochemical equation.
thus N2(g) + O2(g) → 2NO(g); ΔH = + 180.7 kJ is a thermochemical equation
Factors on which the heat of the reaction depends
- Quantities of the reactants involved.
- The physical state of the reactants and products.
- Allotropic modifications
- The concentration of the solutions.
- Temperature
- Conditions of constant pressure or constant volume.
→ Standard Enthalpy Change: A substance in its most stable form at 25°C or 298 K under one atmospheric pressure is said to be in its standard form.
The enthalpy change of reaction when all the reactants and products are in their standard states i.e., at 25°C or 298 K and under a pressure of one bar is called standard enthalpy change.
It is usually represented by ΔrH° or ΔrH298.
Common Types of Enthalpy or Heat Changes
Enthalpy or Heat of formation: The enthalpy of formation is the enthalpy change when one mole a of the compound is formed from its elements. It is deno’.ed by ΔHf.
For example, enthalpies of formation of carbon dioxide and methane (CH4) may be expressed as
C(s) + O2(g) → CO2(g); ΔH = ΔHf=- 395 kJ
C(s) + 2H2(g) → CH4(g); ΔH = ΔHf = -74.8 kJ
If all the species of the chemical reactions are in their standard state, (i.e.. at 298 K and one atmospheric pressure) the enthalpy of formation is called standard enthalpy of formation, expressed as ΔHf.
The enthalpy of every element in its standard state is arbitrarily assumed to be zero.
Thus, the enthalpy change accompanying the formation of one mole of a compound from its elements, all the substances being in their standard states (1 atm pressure and 298 K) is called standard enthalpy of formation.
The enthalpies of the formation of different substances can be used to calculate the enthalpy change of the reaction.
Standard enthalpies of
ΔHf° = formation of all products
or
Standard enthalpies of formation of all reactants
ΔfH° = ΣΔHf° (products) – ΣΔHf° (reactants)
→ Eptnalpy or Heat of combustion: The enthalpy change when 1 mole of a substance is completely burnt in excess of oxygen or air is called enthalpy of combustion. It is expressed as ΔcH°
For example,
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l); ΔfH° = – 890.3 kJ
C6H6(l) + \(\frac{15}{2}\) O2(g) → 6CO2(g) + 3H2O(l); ΔfH° = – 3268 kJ
→ Enthalpy or Heat of solution: The enthalpy change when one mole of a substance is dissolved in a specified quantity of a solvent at a given temperature is called enthalpy of solution.
NH4NO3(s) + H2O(1) → NH4+ NO3– (aq. 1.o m); ΔH = 26.0 kJ
To avoid the amount of solvent, the heat of the solution is usually defined as an infinitely dilute solution. Thus, the heat of solution at infinity dilution is the heat change when one mole of a substance is dissolved in such a large quantity of solvent so that further dilution does not give any further heat change.
NaCl(s) + aq → NaCl(aq); ΔH = 5.0 kJ
→ Enthalpy or Heat of neutralization: The heat change when one gram equivalent of an acid is completely neutralized by a base or vice versa in dilute solution, is called heat of neutralization.
For example,
1. Neutralisation of HCl with NaOH
HCl(aq) + NaOH(aq) → NaCI(aq) + H2O(l); ΔH = – 57.1 kJ
2. Neutralisation of CH3COOH with NaOH
CH3COOH(aq) + NaOH(aq) → CH3COONa + H2O(l); ΔH = – 55.9 kj.
→ Calorific Values of Foods and Fuels: Different fuels and foods produce different amounts of heat on combustion. They are usually expressed in terms of their calorific value. “The calorific value of a fuel or food is the amount of heat in calories (or joules) produced from the complete combustion of 1 gram of the fuel or the food.
e.g., C6H12O6(S) + 6O2(g) → 6CO2(g) + 6H2O(g) + 2840 kJ mol-1
1 Mole = 180 g.
∴ Calorific value of glucose = \(\frac{2840}{180}\) = 15.78 kJ g-1.
→ Measurement of Enthalpy of Combustion: At constant volume (qv or qv = AE) is done in a Bomb calorimeter. The known weight of the compound whose enthalpy of combustion is to determined is burnt in oxygen in a bomb calorimeter
M
ΔE = Q × Δf × \(\frac{M}{m}\)
where Q = Heat capacity of the calorimeter
Δt = rise in temperature of water in the calorimeter
m = mass of the substance taken
M = Molecular mass of the substance
Enthalpy Changes during Phase Transitions
1. Enthalpy of Fusion: It is the heat change accompanying the transformation of one mole of a solid substance into its liquid form at its melting point.
H2O(S) (ice) → H2O(l) (water); ΔHfus = + 60 kJ mol-1
2. Enthalpy of vaporization: It is the heat change accompanying the conversion of 1 mole of a liquid into its gaseous state at its boiling point.
H2O(l) (water) → H2O(g) (steam); Δvap H° = + 407 kJ mol-1
3. Enthalpy of sublimation: It is the heat change that takes place when 1 mol of a solid changes directly into its vapor phase at a given temperature below its melting point.
I2(s) → I2(g); Δsub H° = + 62.39 kJ mol-1
ΔHsublimation = ΔHfusion + ΔHvaporisation
Hess’s Law of Constant Heat Summation
“The total amount of heat evolved or absorbed in a reaction is the same whether the reaction takes place in a single step or in a number of steps, provided the temperature is kept constant.
C(s) + O2(g) → CO2(g); ΔH = – 393.5 kJ mol-1
It can be made to proceed in two steps
- C(s) + \(\frac{1}{2}\)O2(g) → CO(g); ΔH1 = – 110.5 kJ mol-1
- CO(g) + \(\frac{1}{2}\)O2(g) → CO2(g); ΔH2 = – 283.0 kJ mol-1
Thus, the.total heat evolved in steps (1) and (2) is
ΔH1 + ΔH2 = – 110.5 + (- 283.0) = – 393.5 kJ mol-1
which is the same when the reaction takes place directly in a single step.
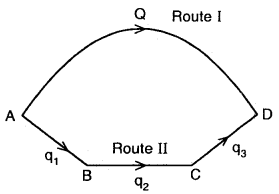
From the above
Heat change is going from A → D via I route = Q
Heat change in going from A → B → C → D via route II = q1 + q2 + q3
∴ Q = q1 + q2 + by Hess’s Law.
It is a corollary from the 1st Law of Thermodynamics.
Applications of Hess’s Law:
- It helps to calculate the enthalpies of the formation of many compounds which cannot be determined experimentally.
- It helps to calculate the enthalpy of allotropic transformations.
- It helps to calculate the enthalpies of hydration.
- It helps to calculate the enthalpies of different reactions.
→ Bond Enthalpy or Bond Energy: It is defined as the amount of energy required to dissociate one mole of bonds presents between the atoms in the gaseous molecules.
H2(g) + 436 kJ mol-1 → 2 H(g)
For diatomic molecules like H2, bond energy is its bond dissociation energy.
→ Spontaneous Process: A process that can take place of its own or has an urge or tendency to take place is called a spontaneous process. It is simply a process that is feasible.
1. Examples of processes that take place by themselves
- Dissolution of common salt in water
- Evaporation of water in an open vessel
- The flow of water downhill
- The flow of heat from the hot end to the cold end.
2. Example of processes that take place on initiation
- Lighting a candle (initiation by ignition)
- Heating of CaCO3 to give CaO and CO2.
→ Non-Spontaneous Process: A process that can neither take place of its own nor on initiation is called a non-spontaneous process.
Examples of non-spontaneous processes.
- The lighting of a candle (initiation by ignition)
- Heating of CaCO3 to give CaO and CO2.
→ Non-Spontaneous Process: A process that can neither takes place of its own nor on initiation is called a non-spontaneous process.
Examples of non-spontaneous processes.
- The flow of water uphill.
- The flow of heat from a cold body to a hot body.
→ The Driving Force for a Spontaneous Process: The force which is responsible for the spontaneity of a process is called the driving force. It is based upon.
- The tendency towards minimum energy: To acquire maximum stability the system tends to acquire minimum energy.
- The tendency towards maximum randomness: When a system proceeds from a state of orderliness to disorderliness as the mixing up of two gases, it tries to have maximum randomness or disorder. An increase in disorder leads to the spontaneity of a process.
→ Entropy: It is a measure of disorder or randomness of the system. Like internal energy, enthalpy, entropy is also a state function and it is an extensive property. ΔS is called a change of entropy.
ΔS = S2 – S1 = ΣSproducts – ΣSreactants
= \(\frac{q_{\text {reversible }}}{\mathrm{T}}\) under isothermal conditions.
Thus Entropy change (ΔS) during a process is defined as the amount of heat (q) absorbed isothermally and reversible divided by the absolute temperature (T) at which the heat is absorbed.
→ Units of Entropy: As ΔS = \(\frac{q}{T}\) = jK-1 mol-1 (S.I. unit)
= Calories K-1 mol-1 (C.G.S. unit)
Entropy Change During Phase Transformations
1. Entropy of fusion (ΔSfusion): The entropy of fusion is the change in entropy when 1 mole of a solid substance changes into its liquid form at its melting point.
Mathematically, ΔSfus = Sliq – Ssolid = \(\frac{\Delta \mathrm{H}_{\text {fusion }}}{\mathrm{T}_{m}}\)
where Tm = Melting point of the solid (K)
ΔHfusion = Enthalpy of fusion per mole.
2. Entropy of Vaporization: It is defined as the entropy change when 1 mole of a liquid changes into its vapor at its boiling point.
Mathematically, ΔSvap = Svap – Sliq = \(\frac{\Delta \mathrm{H}_{\text {vap}}}{\mathrm{T}_{b}}\)
where, ΔHvap = Enthalpy of vaporisation per mole
ΔSvap = entropy of vaporisation
Svap = Molar entropy of vapour
Sliq = Molar entropy of liquid
Tb = Boiling point of the liquid in Kelvin
3. Entropy as a state function: Let us examine entropy as a state function. Consider a cylinder containing a gas and is fitted with a frictionless and weightless piston which is in contact with a large heaf reservoir.
During isothermal and reversible expansion of the gas from volume V1 to V2, the substance will absorb heat, q at temperature T
∴ Change in entropy of the system ΔSsys = \(\frac{q_{\mathrm{rev}}}{\mathrm{T}}\)
Since an equivalent amount of heat will be lost by the reservoir, change in entropy of reservoir will be ΔSres = \(\frac{-q_{\mathrm{rev}}}{\mathrm{T}}\)
Total change in entropy
ΔSt = ΔSsys + ΔSres
= \(\frac{q_{\mathrm{rev}}}{\mathrm{T}}+\left(\frac{-q_{\mathrm{rev}}}{\mathrm{T}}\right)\) = 0
If we compress the gas isothermally from a volume V2 to V1, heat given by the system is, – qrev
ΔSsys = \(\frac{q_{\mathrm{rev}}}{\mathrm{T}}\)
and ΔSres = \(\frac{-q_{\mathrm{rev}}}{\mathrm{T}}\)
Total change in entropy
ΔS1 + ΔS2 = 0
At the end of the cycle, the entropy of the system is the same as it had initially. Therefore, entropy is a state function.
The total entropy change (AStota]) system and surrounding of a spontaneous process is given by
ΔStotal = ΔSsystem + ΔSsurr > 0 When a system is in equilibrium, the entropy is maximum, and the change in the entropy, ΔS = 0.
We can say that entropy for a spontaneous process increases till it reaches maximum but at equilibrium change in entropy is zero. Since entropy is state property, we can calculate the change in – entropy of a reversible process by
ΔSsys = \(\frac{q_{\text {sys rev}}}{\mathrm{T}}\)
We find that both for reversible and irreversible expansion for an ideal gas, under isothermal conditions, ΔU = 0, but ΔStotal i.e., ΔSsys + ΔSsurr is not zero for an irreversible process. Thus ΔH does not discriminate between reversible and irreversible processes, whereas ΔS does.
→ Gibbs energy and spontaneity: We have seen that for a system, it is the total entropy change, ΔStotal which decides the spontaneity of the process But most of the chemical reactions fall into the category of either closed systems or open systems. Therefore, for most of the chemical reactions, there are changes in both enthalpy and entropy. It is clear that neither decrease in enthalpy nor an increase in entropy alone can determine the direction of spontaneous change for these systems.
For this purpose, we define a new thermodynamic function the Gibbs energy or Gibbs function, G, as
G = H -TS
Gibbs function, G is an extensive property and a state function.
The change in Gibbs energy for the system, ΔGsys can be written as
ΔGsys. = ΔHsys – TΔSsys – SsysΔT
At constant temperature,
ΔT = 0 ΔGsys = ΔHsys – TΔS
Usually the subscript ‘system’ is dropped and we simply write this equation as
ΔG = ΔH – TΔS
Thus, Gibbs energy change = enthalpy change – temperature x entropy change, and is referred to as the Gibbs equation, one of the most important equations in chemistry. Here, we have considered both terms together for spontaneity: energy (in terms of ΔH) and entropy (ΔS, a measure of disorder) Dimensionally if we analyzed, we find that ΔG has units of energy because, both ΔH and the TΔS are energy terms (Since TΔS = (K) J/(K mol) = J/mol or J mol-1).
Now let us consider how ΔG is related to reaction spontaneity.
We know, ΔStotal = ΔSsys + ΔSsurr
If the system is in thermal equilibrium with the surroundings, then the temperature of the surrounding is the same as that of the system.
Therefore, an increase in entropy of the surrounding is equal to a decrease in the entropy of the system.
Therefore, entropy change of surroundings,
ΔSsur = – \(\frac{\Delta \mathrm{H}_{\text {surr}}}{\mathrm{T}}\) = – \(\frac{\Delta \mathrm{H}_{\text {sys}}}{\mathrm{T}}\)
ΔSsur = ΔSsys + (- \(\frac{\Delta \mathrm{H}_{\text {sys}}}{\mathrm{T}}\))
Rearranging the above equation:
TΔStotal = TΔSsys -ΔHsys
For spontaneous process,
ΔStotal > 0, so TΔSsys – ΔHsys > 0
Using the equation, the above equation can be written as
ΔG = ΔH – TΔS < 0
ΔHsys is the enthalpy change of a reaction, TΔSsys is the energy that is not available to do useful work. So ΔG is the net energy available to do useful work and is thus a measure of the ‘free energy. For this reason, it is also known as the free energy of the reaction.
ΔG gives a criterion of spontaneity at constant pressure and temperature.
- If ΔG is negative (< 0), the process is spontaneous.
- If ΔG is positive (> 0), the process is nonspontaneous.
Note. If a reaction has a positive enthalpy change and positive entropy change, it can be spontaneous when TΔS is large enough to outweigh ΔH.
This can happen in two ways;
(a) The positive entropy change of the system can be ‘small’ in which case T must be large.
(b) The positive entropy change of the system can be ‘large’, in which case T may be small. The former is one of the reasons why reactions are often carried out at high temperatures.
→ Gibbs Energy Change and Equilibrium: “We have seen how a knowledge of the sign and magnitude of the free energy change of a chemical reaction allows:
- Prediction of the spontaneity of the chemical reaction.
- Prediction of*the useful work that could be extracted from it.
So far we have considered free energy changes in irreversible reactions. Let us now examine the free energy changes in reversible reactions.
‘Reversible’ under strict thermodynamic sense is a special way of carrying out a process such that the system is at all times in perfect equilibrium with its surroundings. When applied to a chemical reaction, the term ‘reversible’ indicates that a given reaction can proceed in either direction simultaneously, so that dynamic directions should proceed with a decrease in free energy, which seems impossible.
Therefore, we say that at equilibrium total free energy of the system is a minimum. If it is not, the system would spontaneously change to the configuration of lower free energy.
So, the criterion for equilibrium
A + B ⇌ C + D; is
ΔrG = 0
Free energy is an extensive property and its value for a given substance will depend on the concentration of the substance. So we have to set its value at an equilibrium concentration as we set temperature and pressure. If the concentrations vary from the equilibrium values, Gibbs energy will also change, we can write
ΔrG = ΔrG° + RT ln Q … (1)
Here, ΔrG° is the difference in standard Gibbs energies of formation of the products and reactants, both in their standard, states. Similarly, ΔrG is the Gibbs energy change at a definite, fixed composition of the reaction mixture. Q is the reaction quotient. R- Gas constant = 8.314 JK-1 mol-1. If the species are gases, these concentrations are expressed in partial pressure, and the reaction quotient will be Qp and if species are in solution, the reaction quotient will be expressed in terms of molar concentration as Q.
At equilibrium, Q = K called equilibrium constant, and ΔrG = 0,
0 = ΔrG° + RT ln K
or
ΔrG° = – 2.303 RT log K
We also know that
ΔrG° = ΔrH° – TΔrS° = – RT ln K …(2)
For strongly endothermic reactions, the value of ArH° may be large and positive. In such a case, the value of K will be much smaller than 1 and the reaction is unlikely to form much product. In the case of exothermic reactions, ΔrH° is large and negative, and ΔrG° is likely to be a large and negative tool. In such cases, K will be much larger than 1. We may expect strongly exothermic reactions to having a large K and hence can go to near completion. ΔrG° also depends upon
ΔrS°, if the changes in the entropy of reaction are also taken into account, the value of K or extent of chemical reaction will also be affected, depending upon whether ΔrS° is positive or negative.
Using equation (2)
- It is possible to obtain an estimate of ΔG° from the measurement of ΔH° and ΔS° and then calculate K at any temperature for economic yields of the products.
- If K is measured directly in the laboratory, the value of ΔG° at any other temperature can be calculated.
Effect of Temperature on Spontaneity of Reactions
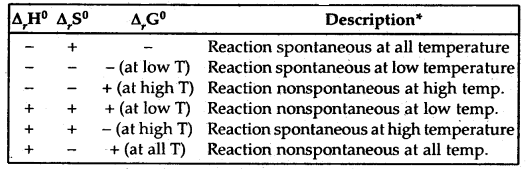
The terms low temperature and high temperature are relative. For a particular reaction, the high temperature could even mean room temperature.
→ System: That part of the universe in which observations are made surroundings. The remaining part of the universe with which the system can exchange both matter and energy is called the surroundings.
There are three types of system:
- Open system
- Closed system
- Isolated system.
→ The state of the system: When the properties of a system like its pressure, volume, temperature, and composition are specified quantitatively, it is said to have a state.
→ State functions or state variables: The average measurable properties like temperature (T), volume (V), pressure (P), and amount (n) of the system are called state functions because their values depend only on the state of the system and not on how it is reached.
Internal Energy: The total energy stored in a system is called its internal energy (U). It may be chemical, electrical, mechanical, or any other type of energy.
(a) Work: It is a form of energy. Work is said to be done if the point of application of a force moves through a certain distance.
Adiabatic process: It is a process in which there is no transfer of heat between the system and surroundings.
Adiabatic system: The system that does not allow the exchange of heat between itself and its surroundings through its boundary is called an adiabatic system.
(b) Heat: The change of internal energy of a system by transfer of heat from the surroundings to the system or vice-versa without the expenditure of work is called heat (q).
Note:
- q is positive when heat is transferred from the surroundings to the system.
- Similarly, w is positive when work is done on the system, w is negative when work is done by the system.
First Law of Thermodynamics:
The energy of an isolated system is constant.
or
Energy can neither be created nor destroyed.
Mathematically, the first law of thermodynamics is
ΔU = q + w
where ΔU is the change of internal energy.
q is the heat absorbed/evolved and iv is the work done
Work done on gas
![]()
= – pexΔV, where pex is the external pressure and ΔV is the change in volume from initial volume Vi to final volume Vf.
→ Reversible process: A process is reversible if it is brought about in such a way that it could at any moment, be reversed by an infinitesimal chance. It proceeds infinitely slowly by a series of 1 equilibrium states such that the system and surroundings are always in equilibrium with each other.
→ Irreversible process: A process or change which is brought, about so rapidly that the system does not get a chance to attain equilibrium. It cannot be retraced at each step of the change.
Under reversible conditions
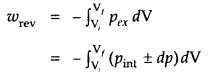
where a pint is the internal pressure of the system. Since dp × dV is very small, we can write
![]()
Writing as (the pressure of the gas inside) p and for n moles of an ideal gas
pV = nRT
p = \(\frac{nRT}{V}\)
∴ Under isothermal conditions (i.e., at constant temperature)
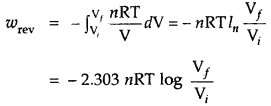
If the gas expands in a vacuum (pext = 0), it is called the free expansion of the gas.
wrev = 0
No work is said to be done during free expansion of a gas whether the process is reversible or irreversible.
Isothermal and free expansion of an ideal gas T = Constant (Isothermal expansion). In vacuum pext = 0
∴ w = 0, q = 0
∴ from ΔU = q + w
ΔU = 0
1. For isothermal irreversible change
q = – w = Pext(Vf – Vi)
2. For isothermal reversible change
q = – w = nRT ln \(\frac{\mathrm{V}_{f}}{\mathrm{~V}_{i}}\)
= 2.303 nRT log \(\frac{\mathrm{V}_{f}}{\mathrm{~V}_{i}}\)
3. For adiabatic change, q = 0
ΔU = w ad
Enthalpy: Sum of internal energy U and the product of pressure and volume (PV) is called enthalpy (H)
Mathematically H = U + pV
Enthalpy change (ΔH) can be written as
ΔH = ΔU + pΔV ………..(1)
ΔH = qp
Thus enthalpy change is the heat absorbed by the system at constant pressure.
- ΔH is negative for exothermic reactions
- ΔH is positive for endothermic reactions
At constant volume
ΔH = ΔU – qv
Thus internal energy change is the heat change at constant volume.
pΔV = Δng RT
where Δng refers to the number of moles of gaseous products minus the number of moles of gaseous reactants.
Substituting the value of pΔV from (2) to (1)
ΔH = ΔU + ΔngRT
→ Extensive Property: An extensive property is one whose value depends on the quantity or size of matter present in the system. For example, mass, volume, internal energy, enthalpy/heat capacity, etc. are extensive properties.
→ Intensive Property: The property which does not depend on the quantity or size of matter present in the system is called Intensive property. For example, temperature, density, pressure is intensive properties.
Heat Capacity (C): It is defined as the quantity of heat energy required to raise the temperature of a substance by 1 K (or 1°C).
q = C × ΔT
where ΔT is the. temperature change
At constant volume the heat capacity C is denoted by Cv
At constant pressure the heat capacity C is denoted by Cp
The relationship between Cp and Cv for an ideal gas
qv = CvΔT = ΔU …….(3)
qp = CpΔT = ΔH ………(4)
For 1 mole of an ideal gas
ΔH = ΔU + Δ(pV)
= ΔU + Δ(RT) [As pV = RT for 1 mole]
or
ΔH = ΔU + RΔT …….(5)
For equations (3) and (4), equation (5) becomes
CpΔT = CvΔT + RΔT
Cp = Cv + R
Cp – Cv = R
Measurement of ΔU and ΔH is done with the help of Calorimeter: Calorimetry is an experimental technique to measure energy changes associated with chemical or physical processes.
The instrument used for it is called a calorimeter.
Enthalpy change ΔrH of a reaction.
ΔrH = (Sum of enthalpies of products) – (sum of enthalpies of reactants)
![]()
Here symbol X(sigma) is used for summation and ai and b{ are the stoichiometric coefficients of the products and reactants respectively in the balanced chemical equation.
Standard enthalpy of reactions: the standard enthalpy of reaction is the enthalpy change for a reaction where all the participating substances are in their standard states.
The standard state of a substance at a specified temperature is its pure form at 1 bar.
Standard enthalpy change is denoted by ΔH°.
Standard enthalpy of fusion or Molar enthalpy of fusion ΔfusH°: The enthalpy change that accompanies melting of one mole of a solid substance in the standard state is called standard enthalpy of fusion or molar enthalpy of fusion Δfus H°.
H2O(S) → H2O(l); ΔfusH° = 6.00 kJ mol-1
→ Standard or Molar enthalpy of Vaporization (Δvap H°): It is the amount of heat required to vaporize one mole of a liquid at constant. temperature and under standard pressure (1 bar).
H2O(l) → H2O(g); ΔvapH° = 40.79 kJ mol-1
→ Standard enthalpy of sublimation (ΔsubH°): It is the enthalpy change when one mole of a solid substance sublimes at a constant temperature and under standard pressure (1 bar).
Solid CO2 or dry ice sublimes at 195 K with ΔsubH° = 25.2 kJ mol-1
→ Standard enthalpy of formation: The standard enthalpy change for the formation of one mole of a compound from its elements in their most stable states of aggregation (also known as reference states) is called Standard Molar Enthalpy of Formation (ΔrH°).
H2(g) + \(\frac{1}{2}\)O2(g) → H2O(l); ΔfH° = – 285,8 kJ mol-1
→ Thermochemical equation: A balanced chemical equation together with the value of its ΔrH is called a thermochemical equation.
C2H5OH(l) + 3O2(g) → 2CO2(g) + 3H2O(l); ΔrH° = – 1367 kJ mol-1
Hess’s Law of Constant Heat
If a reaction takes place in several steps, then its standard reaction enthalpy is the sum of the standard enthalpies of the intermediate reactions into whiter the overall reaction may be divided at the same temperature.
Or
The enthalpy change for a reaction is the same whether it occurs in one step or through a series of steps at the same, temperature.
Standard enthalpy of combustion: It is defined as the enthalpy change when one mole of a substance in its standard state is burnt completely in excess of oxygen or air. (Symbol: ΔCH°).
→ Enthalpy of atomization (ΔaH°): It is the enthalpy change on breaking one mole of bonds completely to obtain atoms in the gas phase.
CH4(g) → C(g) + 4H(g); ΔaH° = 1665 kJ mol-1
Bond Enthalpy (Δbond H°): Two different terms are used
1. Bond dissociation enthalpy: It is the change in enthalpy when one mole of covalent bonds of a gaseous covalent compound is broken to form products in the gas phase.
Cl2(g) → 2Cl(g); ΔCl-Cl H° = 242 kJ mol-1
It is for diatomic molecules like H2, Cl2, O2 in gas phase.
For polyatomic molecules the term used is the mean bond enthalpy. Consider the reaction:
CH4(g) → C(g) + 4H(g); ΔaH° = 1665 kJ mol-1,
ΔC-H° = (ΔaH°) = \(\frac{1}{4}\)(1665 kJ mol-1)
= 416 kJ mol-1
Thus the mean C-H bond enthalpy in methane is 416 kJ mol-1.
→ Enthalpy of Solution (ΔSol H°): It is the enthalpy change when one mole of it dissolves in a specified amount of solvent.
→ Enthalpy of Solution at infinite dilution: It is the enthalpy change observed on dissolving the substance in an infinite amount of the solvent when the interactions between the ions (or solute molecules) are negligible.
→ Lattice Enthalpy: The lattice enthalpy of an ionic compound is the enthalpy change that occurs when one mole of an ionic compound dissociates into its ions in a gaseous state.
Na+Cl–(g) → Na+(g) + Cb(g); ΔlatticeH° = + 788 kJ mol-1
→ Bom-Haber Cycle: It is used to determine the lattice enthalpies. Let us calculate the lattice enthalpy of Na+Cl-(s) by the following steps given below:
- Na(s) → Na(g); ΔsubH° = 108.4 kJ mol-1
- Na(g) → Na+(g) + e–(g); ΔiH° = 496 kJ mol-1
- Cl2(g) → Cl(g); ΔbondH° – 121 kJ mol-1
- Cl(g) + e–(g) → Cl–(g); Δ H° = – 348.6 kJ mol-1
- Na+(g) + Cl–(g) → Na+Cl–(s); ΔlatticeH° = U
Heat of formation of.NaCl(s) is foirnd to be 411.2 kJ mol-1
Na(s) + \(\frac{1}{2}\) Cl2(g) → NaCl(s); ΔFH° = – 411.2 kJ mol-1
Applying Hess’s Law
-411.2 = 108.4 + 121 + 496 – 348.6 + U
or U = – 788 kJ
Thus, lattice energy for NaCl(s) has a large negative value. This explains why the compound NaCl(s) is highly stable.
→ Spontaneous Process: A spontaneous process is an irreversible process and may only be reversed by some external agency.
A decrease in enthalpy is one of the contributing factors for the spontaneity of a process, but it is not true for all cases.
→ Entropy: It is a measure of disorder or randomness of the system like internal energy (U) and enthalpy (H), entropy (S) is a state function.
Change in entropy ΔS = S2 – S1
= ΣSProducts – ΣSreactants
ΔS is related with q and T for a reversible reaction as
ΔS = \(\frac{q_{rev}}{T}\)
For a spontaneous process: The total entropy change (ΔStotal) for the system and surroundings is > 0, i.e.,
ΔStotal = ΔSsystem + ΔSsurf > 0
For a system in equilibrium, the entropy is maximum and change in entropy, ΔS = 0
→ Important Note: For both reversible and irreversible expansion of an ideal gas under isothermal conditions (T = constant) ΔU – 0, but ΔStotal, i.e., ΔSsys+ ΔSsurr is 0 for a reversible process, but not zero for an irreversible process. Thus ΔU does not discriminate between reversible and irreversible processes whereas ΔS does.
→ Gibbs Energy (or Gibbs function): Gibbs energy (G) is an extensive property and it is a state function.
It is the thermodynamic quantity of a system, the decrease in whose value during a process is equal to the maximum possible useful work that can be obtained from the system.
Mathematically G = H – TS
where H is the heat content, T is the absolute temperature and S is the entropy of the system
ΔG = ΔH – TΔS
where ΔG is the change in Gibbs energy, ΔH is the enthalpy change, ΔS is the change in entropy. The above equation is called Gibbs-Helmholtz Equation.
-ΔG = Wnon-expansion = Wuseful
or
– ΔG = Wmax
- If ΔG is negative, the process will be spontaneous.
- If ΔG = 0, the process is in. equilibrium.
- If ΔG is positive, the direct process is non-spontaneous; the reverse process may be spontaneous.
Standard Gibbs energy change is related to the equilibrium constant by
ΔrG° = – RT ln K, where K is equilibrium constant
or
ΔrG° = – 2.303 RT log K.