By going through these CBSE Class 11 Physics Notes Chapter 14 Oscillations, students can recall all the concepts quickly.
Oscillations Notes Class 11 Physics Chapter 14
→ All oscillatory motions are periodic motions but all periodic motions may not be oscillatory.
→ Oscillatory or Vibratory motions are harmonic motions of the simplest type, so they are called simple harmonic motions (S.H.M.).
→ Simple Harmonic Motion is defined as the projection of a uniform circular motion on any diameter of a cycle of reference.
→ The periodic motions are described by fundamental concepts of period$, frequency, amplitude, and displacement.
→ v is the number of oscillations per second.
→ A measurable physical quantity that changes with time is called displacement.
→ The phase difference between displacement and velocity is \(\frac{π}{2}\)
→ The phase difference between displacement and acceleration is π.
→ The S.H.M. is characterized by displacement, amplitude, period, frequency, velocity, acceleration, vibration, and phase.
→ Angular frequency (ω) is related to the period and frequency of the motion by: ω = 2πv = \(\frac{2π}{T}\) .
→ One full oscillation back and forth is known as a cycle or a vibration.
→ A liquid in a U-tube set in oscillations executes S.H.M. with a period T = \(\sqrt{\frac{h}{g}}\), where h is the rise or depression of liquid from the mean position in one limb,
→ The velocity amplitude (vo) of S.H.M. and the acceleration amplitude (ao) are related as follows:
ao = ω vo
→ The necessary and sufficient condition for a particle to execute S.H.M. is that the acceleration is directly proportional to the displacement and is always directed towards the mean position i.e. opposite to the displacement.
→ The work done by a simple pendulum in one complete oscillation is zero.
→ The total energy of S.H.M. is directly proportional to the square of the amplitude.
→ The total energy of S.H.M. is directly proportional to the square of the frequency.
→ The simple pendulum cannot oscillate in weightlessness but the spring can do so.
→ The driving force is a time-dependent force and can be represented by F(t) = fo cos ωt = fo cos 2πvt, v = frequency of driving force.
→ Restoring force must act on the particle executing S.H.M.
→ S.H.M. is represented by y = r sin ωt, where y = displacement of the particle, r = amplitude of oscillation of the particle.
→ Velocity of a particle executing S.H.M. is v = rω cosωt = ω\(\sqrt{r^{2}-y^{2}}\)
→ The maximum velocity of the particle is called velocity amplitude (vo) which is equal to rω.
→ Acceleration of a particle executing a = – ω2y.
→ Acceleration amplitude (i.e. maximum acceleration), ao = ω2r.
→ The velocity of a particle executing S.H.M. is zero at the extreme position and maximum at the mean position.
→ Acceleration is maximum at the extreme position and zeroes at the mean position.
→ The phase difference between velocity and acceleration is \(\frac{π}{2}\)
→ The time period of a simple pendulum is independent of its mass.
→ The graph between l and T2 is a straight line in the case of a simple pendulum.
→ When length of the spring is made n times, its spring constant becomes \(\frac{1}{n}\) times and hence time period will increase \(\sqrt{n}\) times
→ When spring is cut into n equal pieces, the spring constant of each piece will become n times and hence time period will become \(\frac{1}{\sqrt{n}}\) times.
→ The time period of a simple pendulum is oo at the center of the earth because g = 0 at the center of the earth.
→ The time period of a simple pendulum decreases if it accelerates upward with an acceleration a.
→ The time period of a simple pendulum increase if it accelerates downward with an acceleration ‘a’.
→ The time period of the pendulum increases with an increase in length. If its length is increased n times, its time period becomes \(\sqrt{n}\) times.
→ The time period of a simple pendulum increase when it is immersed in a liquid of density σ.
→ The time period of a simple pendulum increase when the temperature of the wire of the bob is increased.
→ The length of a second’s pendulum is 99.3 cm ≈ 1 m.
→ The time period of a simple pendulum of infinite length is 84.6 minutes. In a medium, all oscillations are damped oscillations as their, amplitude decreases with time.
→ Oscillations of a simple pendulum in a room are damped ones.
→ For resonance, frequency of an applied periodic force = natural frequency of the body.
→ The energy-time graph of damped oscillations is shown in the figure here.
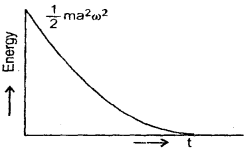
→ Periodic Motion: A motion that repeats itself after regular intervals of time is called periodic motion.
→ Oscillatory or Vibratory Motion: A periodic motion in which a body moves to and fro about a central fixed point (called mean position) is called the oscillatory or vibratory motion of the body of the particle.
→ Driving Force: A time-dependent force applied on an oscillator to increase its vibrations is called a driving force.
→ Second, ’s Pendulum: A pendulum whose time period is 2 seconds is called a second’s pendulum.
→ Undamped Oscillations: The oscillations whose amplitude does not change with time are called undamped oscillations. Such oscillations exist only in a vacuum.
→ Restoring Force: It is defined as the periodic force which comes into play when an object moves away from its equilibrium position while executing S.H.M.
→ Phase: The phase of a vibrating particle at any instant is its state regarding its displacement and direction of vibration at that particular instant. It is denoted by Φ. It is a function of time and is expressed as
Φ = ωt + Φo = \(\frac{2π}{T}\)t + Φo ………..(1)
→ Epoch: It is defined as the initial phase of the vibrating particle i. e. phase at f = 0. It is denoted by Φo. From (1), at t = 0, Φ = Φo.
→ Free Vibrations: When a body vibrates with its own natural frequency, it is said to execute free vibrations.
→ Forced Vibrations: When a body is maintained in a state of vibration by a strong periodic force of frequency other than the natural frequency of the body, the vibrations are said to be forced vibrations.
→ Resonant Vibrations: When a body vibrates with a frequency equal to its natural frequency of vibration, then the vibrations are called resonant vibrations.
→ Resonant vibrations are merely a special case of forced vibrations.
→ Coupled system: A system of two or more oscillators linked together in such a way that there is a mutual exchange of energy between them is called a coupled system.
→ Coupled Oscillations: The oscillations of a coupled system are called coupled oscillations.
→ Force Constant of Spring Constant (k): It is defined as the restoring force per unit displacement, i.e. k = \(\frac{F}{x}\), when F = force, x = displacement of particle executing S.H.M.
→ Phase Difference: The difference in phase angles of two positions of a body or oscillator in periodic motion is called phase difference.
→ Amplitude: The maximum displacement on either side of the mean position of the particle executing S.H.M. is known as the amplitude (A) of the particle.
→ Displacement: Displacement is the change in the position with time from the mean position of oscillatory motion.
→ Period of periodic motion: The smallest time interval after which the process repeats itself is called the period of the periodic motion (T) i.e. It is the time required for one complete cycle or oscillation.
→ Frequency: The reciprocal of the Time Period of motion is known as the frequency. It is the number of oscillations per second, v = \(\frac{1}{T}\).
Important Formulae:
→ Angular frequency/Angular velocity, ω = 2πv = \(\frac{2π}{T}\)
→ Displacement in S.H.M., y(t) = r sin (ωt + Φo).
→ Velocity of particle in S.H.M., v(t) = rωcos (ωt + Φo) = ω\(\sqrt{r^{2}-y^{2}}\)
→ Acceleration in S.H.M., a(c) = – rω2 sin (ωt – Φo) = – ω2y.
→ Time period of a particle in S.H.M. is
T = 2π\(\sqrt{\frac{y}{a}}\) = 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\)
= 2π\(\sqrt{\begin{array}{c}
\text { inertia factor } \\
\hline \text { spring constant }
\end{array}}\)
→ Time period of a mass m suspended by two springs connected in parallel.
T = 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}_{\mathrm{I}}+\mathrm{k}_{2}}}\)
→ Time period of a mass m suspended by two springs connected in . series.
T = 2π\(\sqrt{\left(\frac{1}{k_{1}}+\frac{1}{k_{2}}\right) m}\)
= 2π\(\sqrt{\frac{m\left(k_{1}+k_{2}\right)}{k_{1} k_{2}}}\)
→ Time period of the simple pendulum, T = 2π\(\sqrt{\frac{l}{\mathrm{~g}}}\)
→ Time period of pendulum decreases if it accelerates upward with an acceleration ‘a’ s.t.
T = 2π\(\sqrt{\frac{l}{g+a}}\)
→ Time period of a simple pendulum increases if it accelerates downward with an acceleration ‘a’ s.t.
T = 2π\(\sqrt{\frac{l}{g-a}}\)
→ Time period of a simple pendulum immersed in a liquid of density σ is T’ = T\(\sqrt{\frac{\rho}{\rho-\sigma}}\) = 2π\(\sqrt{\frac{l}{g} \frac{\rho}{(\rho-\sigma)}}\) , ρ = density of the material of the bob.
→ Increase in time period of a simple pendulum with increase in temperature = \(\frac{\alpha \mathrm{d} \theta \mathrm{T}}{2}\), where T = 2π\(\sqrt{\frac{l}{g}}\)
→ Time period of a cylinder floating in a liquid of density ρl, is T = 2π\(\sqrt{\frac{h \rho}{\rho_{l} g}}\) , where h = height of the cylinder, ρ = density of the material of the cylinder, ρl = density of the liquid.
→ Time period of a liquid in a U-tube is
T’ = 2π\(\sqrt{\frac{h}{g}}\) where h = height of liquid column.
→ Energy of a particle in S.H.M. = 2π2 mv2 r2 = \(\frac{1}{2}\) m ω2r2 = \(\frac{1}{2}\) kr2, where ω = angular frequency, r = amplitude, m = mass of particle.
→ Time period of oscillation of a ball in the neck of an air chamber under isothermal conditions is:
T = 2π\(\sqrt{\frac{\mathrm{mV}}{\mathrm{EA}^{2}}}=\frac{2 \pi}{\mathrm{A}} \sqrt{\frac{\mathrm{mV}}{\mathrm{P}}}\)
Where E = coefficient of elasticity
P = atmospheric pressure
m = mass of ball
V = volume of air in the chamber
A = area of cross-section of the neck of the air chamber
Under isothermal conditions E = P.
→ The mechanical energy of damped oscillations for small damping is given by
E(t) = \(\frac{1}{2}\)kxm2 ebt/m
where xm = r = amplitude. It is obtained by replacing r by xmebt/2m in the equation of energy of a particle in S.H.M.
→ The frequency of damped oscillations is given by
W’ = \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}-\frac{\mathrm{b}^{2}}{4 \mathrm{~m}^{2}}}\)