By going through these CBSE Class 11 Physics Notes Chapter 3 Motion in a Straight Line, students can recall all the concepts quickly.
Motion in a Straight Line Notes Class 11 Physics Chapter 3
→ Mechanics is divided into three main branches: Statics, Kinematics and Dynamics.
→ Distance is a scalar quantity.
→ Displacement is a vector quantity.
→ An object is said to be in motion if it changes its position w.r.t. its surroundings as time passes.
→ An object is said to be at rest or it does not change its position w.r.t. its surroundings as time passes.
→ Both rest and motion are relative terms.
→ Distance travelled by a moving body can never be zero or negative i.e. it is always positive.
→ Displacement can be positive, negative or zero.
→ The magnitude of displacement = distance only if a body moves in a straight line without a change in direction.
→ The magnitude of the displacement of a body is the minimum possible distance, so distance ≥ displacement.
→ Speed is a scalar quantity.
→ Velocity is a vector quantity.
→ When a body moves with variable speed, then the average speed of the body is calculated as:
Average speed = \(\frac{\text { Total distance travelled by the body }}{\text { Total time taken }}\)
→ When a body moves with variable velocity, then the average velocity of the body is calculated as:
Average velocity = \(\frac{\text { Total displacement }}{\text { Total time taken }}\)
→ Distance travelled by an object in a given time interval is equal to the area under the velocity-time graph.
→ The direction of velocity and acceleration may not necessarily be the same.
→ The velocity and acceleration of a body may not be zero simultaneously. When the body is in equilibrium, its acceleration is zero.
→ In one, two and three dimensional motions, the object changes its position w.r.t. one, two and three coordinate axes respectively.
→ At a particular instant of time, any point may be chosen as a reference or zero points.
→ The events taking place before the zero time are assigned negative number and events after zero are assigned +ve number.
→ A suitable unit of time say, second, minute or hour may be chosen. In fact, zero points of time and unit of time are chosen according to one’s convenience.
→ The position is also measured with respect to a chosen zero position or origin on the path line.
→ Positions to the right of origin are represented by a positive number and a unit.
→ The position to the left of the origin is represented by a negative number and the unit.
→ For motion in the vertical direction, we can use ‘up’ or ‘down’ instead of ‘right’ and ‘left’.
→ The position is always stated with respect to time,
→ x (t) shows that x is a function of time t.
→ The shift in position x (t’) – x (t) is called the displacement.
→ The rate of change, of displacement, is called velocity.
→ The motion in which an object covers equal distances in equal intervals of time is called uniform motion.
→ Uniform motion may be represented by a straight line parallel to the time axis in a velocity-time graph.
→ It is also represented by a straight line inclined at some angle. The magnitude of velocity is speed.
→ The velocity of a body w.r.t. another body is called its relative velocity.
→ The x-t graph is a straight line parallel to the time axis for a stationary object.
→ Uniformly accelerated motion is a non-uniform motion.
→ When the velocity of the body decreases with time it is said to be decelerated or retarded.
→ When a particle returns to the starting point, its average velocity is zero but the average speed is not zero.
→ For one dimensional motion, the angle between acceleration and velocity is either zero or 180°. It may also change with time.
→ For two dimensional motion, the angle between acceleration and velocity is other than 0° or 180°. It may also change with time.
→ If the angle between a and v is 90°, the path of motion is a circle.
→ If the angle between a and v is other than 0° or 180°, the path of the particle is a curve.
→ For motion with constant acceleration, the graph between x and t is a parabola.
→ For uniform motion, the average velocity is equal to the instantaneous velocity.
→ Statics: It deals with the law of composition of forces and with the conditions of equilibrium of solid, liquid and gaseous states of the objects.
→ Kinematics: It is the branch of mechanics that deals with the study of the motion of objects without knowing the cause of their motion.
→ Dynamics: It is the branch of mechanics that deals with the study of the motion of objects by taking into account the cause of their motion.
→ Point object: It is defined as an object having its dimensions much smaller as compared to the distance covered by it.
→ Acceleration: It is defined as the change in velocity with time i. e.
→ Speed: Theatre of covering distance with time is called speed i.e.
speed = \(\frac{\text { Distance }}{\text { Time }}\)
→ Average speed: It is the ratio of total path length traversed and the corresponding time interval.
→ Velocity: The rate of change of displacement is called velocity.
→ Average velocity: When an object travels with different velocities, its rate of motion is measured by its average velocity.
Average velocity = \(\frac{x_{2}-x_{1}}{t_{2}-t_{1}}=\frac{\Delta x}{\Delta t}\)
→ Instantaneous velocity: The velocity of the object at any particular instant of time is known as instantaneous velocity.
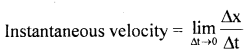
→ Vinst = \(\frac{\mathrm{dx}}{\mathrm{dt}}\)
→ Uniform velocity: A motion in which the velocity of the moving object is constant is called uniform and the velocity is called the uniform velocity. In uniform motion, the object covers equal distances in equal intervals of time along a straight line.
→ Relative velocity: The rate of change in the relative position of an object with respect to the other object is known as the relative velocity of that object.
→ Acceleration: The time rate of change of velocity is known as acceleration.
→ Average acceleration: It is defined as the change in velocity divided by the time interval.
aav = \(\frac{\text { Final velocity – Initial velocity }}{\text { Change in time }}=\frac{v_{2}-v_{1}}{t_{2}-t_{1}}=\frac{\Delta v}{\Delta t}\)
→ Instantaneous acceleration: The acceleration of an object at any instant of time is called instantaneous acceleration. It is also the limiting value of average acceleration.
![]()
→ Retardation: The negative acceleration due to which the body slows down is known as deacceleration or retardation.
→ Non-uniform motion: An object is said to have non-uniform motion when its velocity changes with time even though it has a constant acceleration.
Important Formulae:
→ Displacement in time from t to t’ = x(t’) – x (t)
→ Average velocity, vav = \(\frac{\mathrm{x}\left(\mathrm{t}^{\prime}\right)-\mathrm{x}(\mathrm{t})}{\mathrm{t}-\mathrm{t}}=\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}\)
→ The relative velocity of a body A w.r.t. another body B when they are moving along two parallel straight paths in the same direction is VAB = VA – VB and if they are movinig in opposite direction, then VAB = VA – (-VB) = VA + VB.
Average Speed Vav = \(\frac{\mathrm{S}_{1}+\mathrm{S}_{2}}{\left(\frac{\mathrm{S}_{1}}{\mathrm{v}_{1}}+\frac{\mathrm{S}_{2}}{\mathrm{v}_{2}}\right)}\)
Where S1 is the distance travelled with velocity v1 and S2 is the distant travelled with velocity v2.
→ If S1 = S2, then vav = \(\frac{2 v_{i} v_{2}}{v_{1}+v_{2}}=\frac{2}{\frac{1}{v_{1}}+\frac{1}{v_{2}}}\)
→ Average speed of a body when it travels with speeds v1, v2, v3…..vn in time intervals t1, t2, t3,… tn, respectively is given by
Vav = \(\frac{v_{1} t_{1}+v_{2} t_{2}+v_{3} t_{3}+\ldots .+v_{n} t_{n}}{t_{1}+t_{2}+t_{3}+\ldots+t_{n}}=\frac{\sum_{i=1}^{n} v_{i} t_{i}}{\sum_{i=1}^{n} t_{i}}\)
→ Distance travelled by a body moving with uniform velocity is S = ut.
→ Velocity of an object after a time t in uniformly accelerated motion is, v = u + at.
→ Distance covered by an object after a time t in accelerated motion is, S = ut + \(\frac{1}{2}\)at2.
→ Velocity of an object after covering a distance S in uniformly accelerated motion is, v2 – u2 = 2aS.
→ Distance covered in nth second by a uniformly accelerated object
Snth = u + \(\frac{a}{2}\)(2n – 1)
→ Total time a flight = Time of Ascent + Time of descent.
→ Time of Ascent = Time of descent.