By going through these CBSE Class 11 Physics Notes Chapter 4 Motion in a Plane, students can recall all the concepts quickly.
Motion in a Plane Notes Class 11 Physics Chapter 4
→ All physical quantities having direction are not vectors.
→ The following quantities are neither scalars nor vectors: Relative density, density, frequency, stress, strain, pressure, viscosity, modulus of elasticity, Poisson’s ratio, specific heat, latent leat, a moment of Inertia, loudness, spring constant, Boltzman constant, Stefan’s constant, Gas constant, Gravitational constant, Plank’s constant, Rydberg’s constant etc.
→ A vector can have only two rectangular components in a plane and only three rectangular components in space.
→ Vectors cannot be added or subtracted or divided algebraically.
→ Division of two vectors is not allowed.
→ A vector can have any number of components (even infinite in number but a minimum of two components).
→ Two vectors can be added graphically by using head to tail method or by using the parallelogram or triangle law method.
→ A vector multiplied by a real number gives another vector having a magnitude equal to real number times the magnitude of the given vector and having direction same or opposite depending upon whether the number is positive or negative.
→ Multiplication of a vector by -1 reverses its direction.
→ If A + B = C or A + B + C = 0, then A, B and C are in one place.
→ Vector addition obeys commutative law
i.e. A + B = B + A
→ Vector addition obeys associative law
i.e. (A + B) + C = A + (B + C)
→ Subtraction of B from A is defined as the sum of
– B + A i.e. A – B = A + (-B)
→ The angle between two equal vectors is zero.
→ The angle between -ve vectors is 180°.
→ Unit vector  = \(\frac{\mathbf{A}}{|\mathbf{A}|}\) .
→ The magnitude of  = 1.
→ The direction of A is the same as that of the given vector along which it acts.
→ The resultant of two vectors of unequal magnitudes can never be a null vector.
→ î, ĵ, k̂ are the unit vectors acting mutually perpendicular to each other along X, Y and Z axes respectively and are called orthogonal unit vectors.
→ î.î = ĵ.ĵ = k̂.k̂ = 1
→ î.ĵ = ĵ.k̂ = k̂.î = 0
→ î × î = ĵ × ĵ = k̂ × k̂-= 0
→ î × ĵ = k̂, ĵ × k̂ = î, k̂ × î = ĵ
→ A × A = 0 , Also A – A = 0
But A × A ≠ A – A as A × A ⊥ A and A – A is collinear with A.
→ The cross product:
- Is not commutative (i.e. don’t obey commutative law):
i. e. A × B ≠ B × A
= B × A (anticommutative law) - obeys distributive law i.e.
A × (B + C) = A × B + A × C
→ Vectors lying in the same plane are called co-planer vectors.
→ Vectors are added according to triangle law, parallelogram law, and polygram law of vector addition.
→ The maximum resultant of two vectors A and B is
|Rmax| = |A| + |B|
→ The minimum resultant of two vectors A and B is
|Rmax| = |A| – |B|
→ The minimum number of vectors lying in the same plane whose results can be zero is 3.
→ The minimum number of vectors that are not co-planar and their results can be zero is 4.
→ A minimum number of collinear vectors whose resultant can be zero is 2.
→ A vector in component form is A = Axî + Ayĵ +Azk̂
→ Magnitude of A is = \(\sqrt{A_{x}^{2}+A_{y}^{2}+A_{z}^{2}}\).
→ A projectile is any object thrown with some initial velocity and then it moves under the effect of gravity alone.
→ The trajectory is the path followed by the projectile during its flight.
→ Its trajectory is always parabolic in nature.
→ Two-dimensional motion: The motion of an object in a plane is a two-dimensional motion such as the motion of an arrow shot at some angle and then moving under gravity.
→ Three-dimensional motion: The motion of an object in space is called a three-dimensional motion, for example, the motion of a free gas molecule.
→ Scalar quantities: The quantities which do not need direction for their description are called scalar quantities. Only the magnitude of the quantity is needed to express them correctly. Such quantities are distance, mass, density, energy, temperature etc.
→ Vector quantities: The quantities which need both magnitude and direction for their correct description are called vector quantities. They also obey the law of the addition of vectors. For example displacement, velocity, acceleration, force, momentum etc. are vector quantities.
→ Triangle law of vector addition: If the two vectors are represented by the two adjacent sides of a triangle taken in order, their resultant is given in magnitude and direction by the third side of the triangle taken in the opposite order.
→ Parallelogram law of vector addition: If two vectors acting simultaneously at a point are represented by the two adjacent sides of a parallelogram, then their resultant is completely given in magnitude and direction by the diagonal of the parallelogram passing through that point.
→ Unit vector: A unit vector is a vector in the direction of a given vector whose magnitude is unity. It is represented by a cap or a hat over letter e.g. n̂, î, ĵ, k̂, x̂, ŷ, ẑ etc. The unit vectors in the cartesian coordinate system along the three axes are generally written as î, ĵ and k̂ such that |î| = |ĵ| = |k̂| = 1.
→ Uniform velocity: The uniform or constant velocity is the one in which the moving object undergoes equal displacements in equal intervals of time.
→ Speed: The magnitude of velocity is known as speed. It is the distance travelled divided by the time taken.
→ Uniform acceleration: When the velocity of an object changes by equal amounts in equal intervals of time, the object is said to be having uniform acceleration.
→ Projectile: Projectile is a particle or an object projected with some initial velocity and then left to move under gravity alone.
→ The uniform circular motion: The motion of an object in a circular path with constant speed and constant acceleration (magnitude) is called a uniform circular motion.
→ Equal vectors: Two vectors are said to be equal if they have the same magnitude and act in the same direction.
→ Negative vector: A vector having the same magnitude as the given vector but acting in exactly the opposite direction is called a negative vector.
→ Co-initial vectors: Vectors starting from the same initial point are called co-initial vectors.
→ Zero vector or Null vector: The vector whose magnitude is zero but the direction is uncertain (or arbitrary) is called a zero or null vector. It is represented by 0.
→ Collinear vectors: Two vectors acting along the same or parallel lines in the same or opposite directions are called collinear vectors.
→ Fixed vector: A vector whose tail point or initial point is fixed is called a fixed vector.
→ Free vector: A vector whose initial point or tail is not fixed is called a free vector.
→ Polygon law of addition of vectors: It states that if a number of vectors are represented by the sides of a polygon taken in the same order, then their resultant is given completely by the closing side of the polygon taken in the opposite order.
→ Rectangular components of a vector in a plane: The resolution of a vector into two mutually perpendicular components in a plane is called rectangular resolution and each component is called a rectangular component.
→ Rectangular components in a plane: The components of a vector along three mutually perpendicular axes are called the rectangular component of a vector in space.
→ Scalar product of vectors: If the multiplication of two vectors yields a scalar quantity, the multiplication is called a scalar or dot product. This is because of the fact that multiplication is denoted by a dot (.) between the multiplying vectors e.g. A.B = AB cos θ, where θ is the angle between the two vectors.
→ Cross or vector product: When the multiplication of two vectors is shown by a cross (×) between them, it is called a cross product. The resultant is also a vector quantity e.g. A × B = C. This multiplication is, therefore, also known as the vector product.
Important Formulae:
→ Uniform circular motion: Time period T second, frequency
v = \(\frac{1}{T}\)
Angular velocity ω = \(\frac{θ}{T}\),
ω = \(\frac{2 \pi}{\mathrm{T}}\) = 2πv,
v = \(\frac{1}{T}\),
θ = \(\frac{l}{r}\)
or
l = rθ.
→ Angular acceleration: α = \(\frac{\omega_{2}-\omega_{1}}{t_{2}-t_{1}}=\frac{d \omega}{d t}\)
average acceleration, aav = \(\frac{v_{2}-v_{1}}{t_{2}-t_{1}}\)
Average angular acceleration,
![]()
→ Time for maximum height: t = \(\frac{\mathrm{u} \sin \theta}{\mathrm{g}}\)
→ Angle of projection of maximum horizontal range:
θ = \(\frac{π}{4}\) or 45°.
→ Angles for same range θ, (\(\frac{π}{2}\) – θ)
→ General position – velocity – acceleration relations:
Δr (t) = r(t + Δt) – r(t)
v(t) = \(\frac{\Delta \mathrm{x}(\mathrm{t})}{\Delta \mathrm{t}}\);
vx(t) = \(\frac{\Delta \mathrm{x}(\mathrm{t})}{\Delta \mathrm{t}}\),
vy(t) = \(\frac{\Delta \mathrm{y}(\mathrm{t})}{\Delta \mathrm{t}}\)
Δx(t) = x(t + Δt) – x(t)
Δy(t) = y(t + Δt) – y(t)
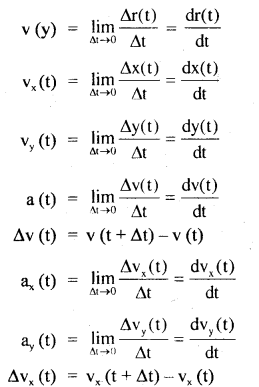
→ Since: A.A = A2, so
- î.î =1,
- ĵ.ĵ =1,
- k̂.k̂ =1
As î, ĵ and k̂ are mutually perpendicular so
î.ĵ = ĵ.k̂ =0,
k̂.î = 0
→ A.(B + C) = A.B. +A.C
→ Vector product:
A × B = C = |A| |B|sin θ n̂
In cartesian coordinates,
A × B = (Axî + Ayĵ + Azk̂) × (Bxî + Byĵ + Bzk̂)
= (AyBz – AzBy) î + (AzBx – AxBz)ĵ + (AxBy – AyBx)k̂
= \(\left|\begin{array}{ccc}
\hat{\mathrm{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\
\mathrm{A}_{\mathrm{x}} & \mathrm{A}_{\mathrm{y}} & \mathrm{A} \\
\mathrm{B}_{\mathrm{x}} & \mathrm{B}_{\mathrm{y}} & \mathrm{B}
\end{array}\right|\)
→ A × B ≠ B × A
= -B × A
→ |A × B|2 + |A . B|2 = 2|\(\overrightarrow{\mathrm{A}}\)|2|\(\overrightarrow{\mathrm{B}}\)|2
→ Direction cosines:
cos α = \(\frac{A_{x}}{A}\) = l,
cos β = \(\frac{A_{y}}{A}\) = m, and
cos γ = \(\frac{A_{z}}{A}\) = n
→ l2 + m2 + n2 = 1
→ Velocity: v = vxi + vyj
→ Speed: v = |v| = (vx2 + vy2)1/2 .
→ Distance travelled in time t:
x(t)î + y(t)ĵ = x(0)î + y(0)ĵ + (vxî + vyĵ)t
→ x (t) = x (0) + vxt
→ y (t) = y (0) + vyt
→ Average velocity:
Vaverage = \(\frac{\left|r\left(t^{\prime}\right)-r(t)\right|}{t^{\prime}-t}=\frac{r_{12}}{\left(t_{2}-t_{1}\right)}=\frac{\Delta r}{\Delta t}\)
→ Instantaneous velocity:
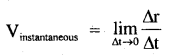
→ Scalar product of A and B is
A . B = AB cos θ, where θ = angle between A and B.
→ Scalar (or Dot) product always gives a scalar quantity.
→ When A. B = 0 then A and B are perpendicular to each other.
→ A . B in component form is
A.B = AxBx + AyBy + AzBz.
→ Cross product of A and B is
A × B = (AB sin θ) n̂ = C
where n̂ = unit vector ⊥ to the plane containing A and B i.e. n̂ acts along C.
→ If we move anticlockwise, n is vertically upward i.e. +ve.
→ If we move clockwise, n vertically downward i.e. -ve.
→ Maximum height attained by the projectile fired at an angle 0 with the horizontal with velocity u is
H = \(\frac{\mathbf{u}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}\)
→ Time of flight = T = \(\frac{2 u \sin \theta}{g}\)
→ Time of maximum height attained = Time of ascent = Time of descent = \(\frac{u \sin \theta}{g}\)
→ Horizontal range of the projectile is R = \(\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}\)
→The range of projectile is maximum if θ = 45°.
→ Rmax = \(\frac{\mathrm{u}^{2}}{\mathrm{~g}}\)
→ When the range is maximum, the maximum height attained by the projectile (Hm) is
Hm = \(\frac{u^{2}}{4 g}=\frac{R_{\max }}{4}\)
→ For Rmax , Tmax = \(\frac{\mathrm{u}}{\sqrt{2} \mathrm{~g}}\)
→ When θ = 90, Hmax = \(\frac{u^{2}}{2 g}\) and is twice the maximum height attained by the projectile when range is maximum.
→ For θ = 90°, Time of flight is Maximum = \(\frac{2 \mathrm{u}}{\mathrm{g}}\)
→ Horizontal range is same for two angles of projections i.e. θ and 90 – θ with the horizontal.
→ If an object is moving in a plane with constant acceleration a, then a = \(\sqrt{\mathrm{a}_{\mathrm{x}}^{2}+\mathrm{a}_{\mathrm{y}}^{2}}\)
→ If r0 be the position vector of a particle moving in a plane at time t = 0, then at any other time t, its position vector will be
r = ro + vot + \(\frac{1}{2}\) at2
where v0 = its velocity at t = 0.
→ Its velocity at time t will be v = vo + at.
→ When the object moves in a circular path at constant speed, then its motion is called uniform circular motion. The angle described by the rotating particle is called angular displacement.
→ Angular displacement, Δθ = \(\frac{\Delta l}{\mathrm{r}}\) .
→ Angular velocity, ω = \(\frac{\Delta \theta}{\Delta \mathrm{t}}\)
Instantaneous angular velocity, ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\)
ω = \(\frac{2 \pi}{\mathrm{T}}\) = 2πv (∵ v = \(\frac{1}{T}\))
Angular velocity (ω) of a rigid body rotating about a given axis is constant, so v is different for different particles of the body.
Angular acceleration α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}=\frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}\)
Tangential acceleration is a1 = α × r and at is directed along the tangent to the circular path.
→ Centripetal acceleration (ac) is given by ac = \(\vec{\omega}\) × v and it is directed towards the centre of the circular path. Thus acceleration of the particle is
a = at + ac
then at ⊥ ac
∴ |a| = \(\sqrt{a_{1}^{2}+a_{c}^{2}}\)
→ Also \(\vec{\omega}\) ⊥v as to and a are parallel to Δθ. i.e. they are directed along the axis of rotation
Hence ac = ω v sin 90
ac = ω v = ω . rω = rω2
= \(\frac{v^{2}}{r}\)
→ Centripetal force, Fc = mac = \(\frac{m v^{2}}{r}\) = mrω2.
→ Fc is always directed towards the centre of the circular path.
→ The Axis of rotation is perpendicular to the plane of rotation.
→ There can be no circular motion without centripetal force. Centripetal force can be a mechanical, electrical or magnetic force in nature.
→ Fc is always ⊥ to the velocity of the particle.
→ θ, ω, α are called axial vectors or pseudo vectors.
→ Tangential acceleration is equal to the product of angular acceleration and the radius of the circular path i.e. at = rα.