By going through these CBSE Class 11 Physics Notes Chapter 7 Systems of Particles and Rotational Motion, students can recall all the concepts quickly.
Systems of Particles and Rotational Motion Notes Class 11 Physics Chapter 7
→ C.M. of a body or a system may or may not lie inside the body.
→ The momentum of the C.M. of the system remains constant if the external force acting on it is zero.
→ C.M. of the system moves with a constant velocity if the external force on the system is zero.
→ Only the angular component of the force gives rise to torque.
→ Both angular momentum and torque are vector quantities.
→ The rotatory cum translatory motion of a ring, disc, cylinder, spherical shell, or solid sphere on a surface is called rolling.
→ The axis of rotation of the rolling body is parallel to the plane on which it rolls.
→ When the angular speed of all the particles of the rolling body is the same, it is called rolling without slipping.
→ The linear speed of different particles is different, although the angular speed is the same for all the particles.
→ K.E. is the same for all bodies having the same m, R, and ω.
→ Total energy and rotational kinetic energy are maximum for the ring and minimum for the solid sphere.
→ For ring Kr = Kt, Kr = \(\frac{1}{2}\) Kt for disc, Kr = 66%Kt for spherical shell and for solid sphere Kr = 40% of Kt.
→ The body rolls down the inclined plane without slipping only when the coefficient of limiting friction (p) bears the following relation:
µ ≥ (\(\frac{\mathrm{K}^{2}}{\mathrm{~K}^{2}+\mathrm{R}^{2}}\)) tan θ
→ The relative values of p for rolling without slipping down the inclined plane are as follows :
μring > μshell > μdisc > μsolid sphere
→ When a body roll Is without slipping, no work is done against friction.
→ A body may roll with slipping if friction is less than a particular value and it may roll without slipping if the friction is sufficient.
→ M.I. is not a scalar quantity because for the same body its values are different for different orientations of the axis of rotation.
→ M.I. is defined w.r.t. the axis of rotation.
→ M.I. is not a vector quantity because the clockwise or anticlockwise direction is not associated with it.
→ The radius of gyration depends on the mass and the position of the axes of rotation.
→ M.I. depends on the position of the axis of rotation.
→ The theorem of ⊥ar axes is applicable to thin laminae like a sheet, disc, ring, etc.
→ The theorem of || axes is applicable to all types of bodies.
→ M.I. about the axis in a particular direction is least when the axis of rotation passes through the C.M.
→ A pair of equal and opposite forces with different lines of action is known as a couple.
→ A body may be in partial equilibrium i.e. it may be in translational. equilibrium and not in rotational equilibrium or vice-versa.
→ If the sum of forces is zero, it is said to be in translational equilibrium. 0 If the sum of moments of forces about C.G. is zero then it is said to be in rotational equilibrium.
Important Formulae:
→ Position vector of C.M. of a system of two particles is
Rcm = \(\frac{\mathrm{m}_{1} \mathbf{r}_{1}+\mathrm{m}_{2} \mathbf{r}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\)
→ Position vector of C.M of a system of two particles of equal masses is
Rcm = \(\frac{\mathbf{r}_{1}+\mathbf{r}_{2}}{2}\)
→ Torque acting on a particle is given by
τ = r × p
→ Angular momentum is given by
L = r × p
or
L = mv r = Iω = mr² ω
→ τ = \(\frac{\mathrm{dL}}{\mathrm{dt}}\)
→ τ = Iα
→ I1ω1 = I2ω2
or
\(\frac{I_{1}}{T_{1}}=\frac{I_{2}}{T_{2}}\)
→ K.E. of rotation, Kt = \(\frac{1}{2}\)Iω2
→ Power in rotational motion, P = τω
→ According to theorem of perpendicular axes,
Iz = Ix + Iy
→ According to theorem of || axes, 1 = Ic + mh2
→ K.E. of a body rolling down an inclined plane is given by
E = \(\frac{1}{2}\)mv2 + \(\frac{1}{2}\) Iω2 = Kt + Kr
→ \(\frac{K_{r}}{K_{t}}=\frac{\frac{1}{2} I \omega^{2}}{\frac{1}{2} m v^{2}}=\frac{\frac{1}{2} m K^{2} \omega^{2}}{\frac{1}{2} m v^{2}}\)
= \(\frac{\mathrm{K}^{2} \omega^{2}}{\mathrm{R}^{2} \omega^{2}}=\frac{K^{2}}{\mathrm{R}^{2}}\)
→ \(\frac{\mathrm{K}_{\mathrm{r}}}{\mathrm{E}}=\frac{\frac{1}{2} \mathrm{mK}^{2} \omega^{2}}{\frac{1}{2} \mathrm{~m}\left(\mathrm{R}^{2}+\mathrm{K}^{2}\right) \omega^{2}}=\frac{\mathrm{K}^{2}}{\mathrm{~K}^{2}+\mathrm{R}^{2}}\)
→ \(\frac{K_{t}}{E}=\frac{R^{2}}{R^{2}+K^{2}}\)
→ If inclined plane is smooth, then the body will slide down and on reaching the bottom, its sliding velocity (Vs) is given by
Vs = \(\sqrt{2 \mathrm{gh}}\) and acceleration is as = g sin θ.
→ For rough inclined plane :
Vr = \(\frac{\sqrt{2 \mathrm{gh}}}{\sqrt{1+\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}}}\)
→ The acceleration of the body rolling down the inclined plane is
ar = \(\frac{g \sin \theta}{\sqrt{1+\frac{K^{2}}{R^{2}}}}\)
→ Time taken to reach the bottom is ts = \(\sqrt{\frac{2 l}{a_{s}}}\) and tr = \(\sqrt{\frac{2 l}{a_{r}}}\)
→ If a particle of mass m is moving along a circular path of radius r with acceleration ‘a’, then
τ = mr² α
Where α = \(\frac{a}{r}\)
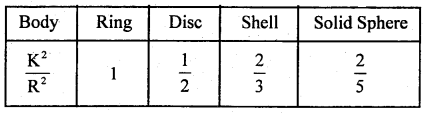
→ The value of \(\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\) for different bodies are as follows: