Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 12 Thermodynamics. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.
Class 11 Physics Chapter 12 Important Extra Questions Thermodynamics
Thermodynamics Important Extra Questions Very Short Answer Type
Question 1.
What type of process is Carnot’s cycle?
Answer:
Cyclic process.
Question 2.
Can the Carnot engine be realized in actual practice?
Answer:
No. It is an ideal heat engine.
Question 3.
A refrigerator transfers heat from a cold body to a hot body. Does this not violate the second law of thermodynamics?
Answer:
No. This is because external work is being performed.
Question 4.
What is a heat pump?
Answer:
A heat pump is a device that uses mechanical work to remove heat.
Question 5.
What forbids the complete conversion of work into heat?
Answer:
The second law of thermodynamics.
Question 6.
Does the internal energy of an ideal gas change in:
(a) an isothermal process?
Answer:
No.
(b) an adiabatic process?
Answer:
Yes.
Question 7.
What is the specific heat of a gas in an isothermal process and in an adiabatic process? Why?
Answer:
It ¡s infinite in isothermal process because ΔT = 0 (C = \(\frac{\Delta Q}{m \Delta T}\)) and zero in an adiabatic process as ΔQ = 0.
Question 8.
Can the temperature of an isolated system change?
Answer:
Yes, in an adiabatic process the temperature of an isolated system changes. It increases when the gas is compressed adiabatically.
Question 9.
Can we increase the coefficient of performance of a refrigerator by increasing the amount of working substance?
Answer:
No.
Question 10.
The door of an operating refrigerator is kept open in a closed room. Will it make the room warm or cool?
Answer:
The room will be slightly warmed.
Question 11.
How is the heat engine different from a refrigerator?
Answer:
A refrigerator is a heat engine working in the reverse direction.
Question 12.
What is the nature of the P – V diagram for isobaric and isochoric processes?
Answer:
The P – V diagram for an isobaric process is a straight line parallel to the volume axis while for an isochoric process, it is a straight line parallel to the pressure axis.
Question 13.
Mention two essential characteristics of an ideal heat engine.
Answer:
- It should have a source of infinite thermal capacity.
- It should have a sink of infinite thermal capacity.
Question 14.
Under that ideal condition can the efficiency of a Carnot engine be 100%?
Answer:
The efficiency of a Carnot engine can be 100% if the temperature of the sink is zero kelvin.
Question 15.
In summer, when the valve of a bicycle tube is removed, the escaping air appears cold. Why?
Answer:
This happens due to the adiabatic expansion of the air of the tube of the bicycle.
Question 16.
When the air of the atmosphere rises up, it cools. Why?
Answer:
When air rises up, it expands due to a decrease in the atmospheric pressure and thus temperature falls. So it cools.
Question 17.
Why does gas get heated on compression?
Answer:
Because work is done in compressing the gas increases the internal energy of the gas.
Question 18.
Which one among a solid, liquid, and gas of the same mass and at the same temperature has the greatest internal energy and which one has the least?
Answer:
Gas has the greatest internal energy and a solid has the least internal energy.
Question 19.
Can two isothermal curves intersect each other?
Answer:
No.
Question 20.
Does a gas work when it expands adiabatically is the source of energy?
Answer:
Yes.
Question 21.
Name the forces ¡n a system that makes the process taking place in it irreversible in nature.
Answer:
All types of dissipative forces in a system make the process taking place irreversible, e.g. force of friction is a dissipative force.
Question 22.
Is rusting of iron a reversible process? Why?
Answer:
Yes. Rusting of iron is an irreversible process as it is a chemical change.
Question 23.
State the conditions for irreversible processes.
Answer:
The following are the conditions for irreversible processes:
- Rapidly carried out the process.
- Dissipation of energy by any means.
Question 24.
How can we cause heat to flow from a body at a lower temperature to one at a higher temperature?
Answer:
This can be caused by doing work on an engine that works in a reverse direction.
Question 25.
Can water be made to boil without heating? How?
Answer:
Yes, by reducing the pressure on the water its boiling point can be brought to room temperature.
Question 26.
Can a room be cooled by leaving the door of an electric refrigerator opens?
Answer:
No.
Question 27.
How much is CP greater than Cv?
Answer:
CP is greater than Cv by R i.e. universal gas constant.
Question 28.
As CP – Cv is constant for all gas, is CP/Cv also constant for all gases?
Answer:
No.
Question 29.
What remains constant in an adiabatic process?
Answer:
Heat contents of the system remain constant in an adiabatic process.
Question 30.
Can heat be added to a system without changing its temperature?
Answer:
Yes.
Question 31.
Do water and ice have the same specific heat? Tell their values.
Answer:
No. For water specific heat is 1 and for ice, it is 0.5 in C.G.S. units.
Question 32.
What is the amount of work done in a cyclic process?
Answer:
The area enclosed under the P – V loop gives the amount of work done in a cyclic process.
Question 33.
What factors determine the internal energy of a real gas?
Answer:
Volume and temperature determine the internal energy of a real gas.
Question 34.
Can the temperature of gas be increased without adding heat into it? How?
Answer:
Yes. It can be done by compressing the gas adiabatically.
Question 35.
Why can’t the engine of a ship be operated using the internal energy of seawater?
Answer:
It is because a sink at low temperature is not available in the sea.
Question 36.
Is melting of ice an adiabatic or an isothermal process?
Answer:
The melting of ice is an isothermal process.
Question 37.
Can PV = RT describe an isothermal or adiabatic process?
Answer:
It can describe an isothermal process but not the adiabatic process.
Question 38.
Tell the main features of the first law of thermodynamics.
Answer:
It tells us about the conversion of mechanical energy into heat energy.
Question 39.
What are the main features of the second law of thermodynamics?
Answer:
It tells that entire heat energy can’t be converted into mechanical energy or heat can’t itself flow from lower temperature to higher temperature body.
Question 40.
What is the significance of knowing the ratio of CP and Cv for a gas?
Answer:
It gives the atomicity of the gas as well as is an indicator of the degrees of freedom of gas molecules.
Question 41.
You enjoy shower bathing in summer but not in winter. Why?
Answer:
Water in the shower cools down due to adiabatic expansion, thus we would like to take bath in cold water in summer but not in winter.
Question 42.
Why the specific heats of argon, nitrogen, and ether are different at constant pressure?
Answer:
Argon, nitrogen, and ether have different atomicities. Hence additional heat is needed to raise the temperature by 1°C due to rotational and vibrational motion in bi, tri, and polyatomic gases, hence the difference.
Question 43.
Distinguish the formulae CP – Cv = R, CP – Cv = R/J and CP – Cv = r/J.
Answer:
- CP – Cv = R is used for a mole of the gas when CP and Cv are measured in joule.
- CP – Cv = R/J is used when CP and Cv are measured in calories.
- CP – Cv = r/J is used for a unit mass of gas, CP and Cv are in calories.
Question 44.
Define an adiabatic process.
Answer:
It is defined as the process in which no heat enters or leaves the system.
Question 45.
State second law of thermodynamics.
Answer:
It states that heat itself can’t flow from a body at a lower temperature to a body at a higher temperature.
Question 46.
Define an isothermal process.
Answer:
It is defined as the process which takes place at a constant temperature.
Question 47.
Define an isotherm.
Answer:
It is defined as the pressure-volume curve for a fixed temperature.
Question 48.
Name the types of thermodynamic state variables.
Answer:
They are of the following two types:
- extensive
- intensive.
Question 49.
Define a cyclic process.
Answer:
It is defined as the process in which the system returns to its initial state.
Question 50.
(a) Is .the specific heat of water greater than that of sand?
Answer:
Yes. Actually, the specific heat of water is maximum.
(b) What is the important difference between the P – T diagram of water and that of CO2?
Answer:
The slope of the fusion curve is negative for water and positive for CO2.
Thermodynamics Important Extra Questions Short Answer Type
Question 1.
Kelvin and Clausius’s statements of the Second law of thermodynamics are equivalent. Explain?
Answer:
Suppose we have an engine that gives a continuous supply of work when it is cooled below the temperature of its surroundings.
This is a violation of Kelvin’s statement. Now if the work done by the engine is used to drive a dynamo which produces current and this current produces heat in a coil immersed in hot water, then w,e have produced a machine which causes the flow of heat from a cold body to the hot body without the help of an external agent. This is a violation of Clausius’s statement. Hence both statements are equivalent.
Question 2.
Two identical samples of gas are expanded so that the volume is increased to twice the initial volume. However, sample number 1 is expanded isothermally while sample number 2 is expanded adiabatically. In which sample is the pressure greater? Why?
Answer:
Pressure is greater in sample number 1 as can be explained: For isothermal expansion.
P1V1 = P2V2 for no. 1 sample
Now V2 = 2V1
∴ P1V1 = P22V1
or
P2 = \(\frac{P_{1}}{2}\) …(i)
Now for adiabatic expansion (for sample 2)
P1V1γ = P2V2γ
or
P2 = P1\(\left(\frac{\mathrm{V}_{\mathrm{1}}}{\mathrm{V}_{2}}\right)^{\gamma}\) = P1\(\left(\frac{\mathrm{V}_{1}}{2 \mathrm{~V}_{1}}\right)^{\gamma}\)
= \(\frac{P_{1}}{2^{\gamma}}\) …(ii)
∴ From (i) and (ii) we find that pressure is greater in sample 1 as γ > 1.
Question 3.
No real engine can have an efficiency greater than that of a Carnot engine working between the same two temperatures. Why?
Answer:
A Carnot engine is an ideal engine from the following points of view:
- There is no friction between the walls of the cylinder and the piston.
- The working substance is an ideal gas i.e. the gas molecules do not have molecular attraction and they are points in size.
However these conditions cannot be fulfilled in a real engine and hence no heat engine working between the same two temperatures can have an efficiency greater than that of a Carnot, engine.
Question 4.
Explain why two isothermal curves cannot intersect each other?
Answer:
If they intersect, then at the point of intersection, the volume and pressure of the gas will be the same at two different temperatures which is not possible.
Question 5.
What is the source of energy when gas does work when expands adiabatically?
Answer:
During adiabatic expansion, the temperature and hence the internal energy of the gas decreases. Thus work is done by the gas at the cost of its internal energy.
Question 6.
State and explain the zeroth law of thermodynamics?
Answer:
It states that if two systems A and B are in thermal equilibrium with a third system C, then A and B must.be in thermal equilibrium with each other.
Explanation: The three systems are shown in the figure. Let T1, T2, T3 be the temperatures of A, B, and C respectively.
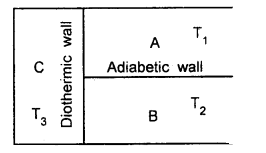
Systems A and C, B and C will exchange heat and after a certain time, they will attain thermal equilibrium separately.
i.e. T1 = T3 ….(1)
and T2 = T3 …. (2)
Thus from (1) and (2),
T1 = T2
i.e. A and B are now in thermal equilibrium with each other.
Question 7.
State and explain the first law of thermodynamics. What are the sign conventions?
Answer:
It states that if an amount of heat dQ is added to a system then a part of it may increase its internal energy by an amount dU and the remaining part may be used up as the external work dW done by the system i.e. mathematically,
dQ = dU + dW
= dU + PdV
Sign conventions:
- Work done by a system is taken as positive while the work done on the system is taken as -ve.
- The increase in the internal energy of the system is taken as positive while the decrease in the internal energy is taken as negative.
- Heat added (gained) by a system is taken as positive and the heat lost by the system is taken as negative.
Question 8.
Why cannot a ship use the internal energy of seawater to operate the engine?
Answer:
The heat engine can convert the internal energy of seawater if there is a sink at a temperature lower than the temperature of seawater. Since there is no such sink and hence a ship can’t use the internal energy of seawater to operate the engine.
Question 9.
A certain amount of work is done by the system in a process in which no heat is transferred to or from the system. What happens to the internal energy and the temperature of the system?
Answer:
The temperature of the system decreases as the system is doing work and no heat transfer is allowed to or from the system. As the temperature of the system decreases, the internal energy of the system also decreases.
Question 10.
If an electric fan is switched on in a closed room, will the air of the room be cooled? Why?
Answer:
No. It will not be cooled, rather it will get heated because the speed of the air molecules will increase due to the motion of the fan. We feel cooler because of the evaporation of the sweat when the fan is switched on.
Question 11.
Define coefficient of performance.
Answer:
It measures the efficiency of a refrigerator. It is defined as the ratio of the quantity of heat removed per cycle from the contents of the refrigerator to the work done by the external agency to remove it. It is denoted by β or ω or K.
Question 12.
State the principle of a refrigerator.
Answer:
A refrigerator may be regarded as Carnot’s ideal heat engine working in the reverse direction. Thus when a Carnot engine works in opposite direction as a refrigerator, it will absorb an amount of heat Q2 from the sink (contents of the refrigerator) at lower temperature T2. As heat is to be removed from the sink at a lower temperature, an amount of work equal to Q1 – Q2 is performed by the compressor of the refrigerator to remove heat from the sink and then to reject the total heat
Q1 = (Q2 + Q1 – Q2)
to the source (atmosphere) through the radiator fixed at its back. It is also called a heat pump.
Question 13.
Derive the expression for the coefficient of performance.
Answer:
We know that by def. β = \(\frac{\text { Heat removed } / \text { cycle }}{\text { Work done } / \text { cycle }}\)
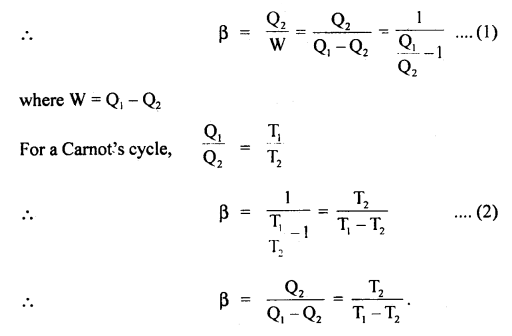
Question 14.
What do you conclude about the coefficient of performance?
Answer:
- In actual practice, β varies from 2 to 6. For an actual refrigerator, the value of β is less than that calculated from equations (1) and (2).
- The lesser the difference between the temperatures of the cooling chamber and the atmosphere, the higher is the p.
- P can be much higher than 100% but η of a heat engine can never exceed 100%.
- As the refrigerator works, T2 goes on decreasing due to the formation of too much ice. There is practically no change in T1. This decreases the value of β. However, if the refrigerator is defrosted, T2 shall increase, and hence the value of β. So it is necessary to defrost the refrigerator.
Question 15.
Milk is poured into a cup of tea and is mixed with a spoon. Is this an example of a reversible process? Give reason.
Answer:
No. It is an example of an irreversible process. When milk is poured into a cup of tea and mixed, some work is performed and the same gets converted into heat. It is not possible to convert the heat produced back into work which will separate the milk from the tea.
Question 16.
Explain whether the following processes are reversible?
(a) Waterfall,
Answer:
The falling of water is not a reversible process. During the waterfall, the major part of its potential energy is converted into kinetic energy of the water and on striking the ground, a part of it is converted into heat and sound. It is not possible to convert the heat and sound produced along with the K.E. of water into the potential energy so that the water will rise back to its initial height.
(b) Electrolysis.
Answer:
It is a reversible process if the electrolyte does not offer any resistance to the flow of current. If we reverse the direction of the current, the direction of motion of ions is also reversed.
Question 17.
State the conditions for reversible and irreversible processes.
Answer:
Conditions for the reversible process:
- The process should be slow enough so that at each stage of operation the system is in:
(a) Mechanical equilibrium with the surroundings.
(b) Chemical equilibrium with the surroundings. - There should not be a loss of energy due to friction.
- Energy should not be lost due to conduction, convection, and radiation during the process.
Question 18.
Why cooling takes place when gas suffers adiabatic expansion?
Answer:
When a gas expands under adiabatic condition, then dQ = 0 and thus dU + dW = 0. So the gas does„external work for its expansion at the cost of internal energy due to which temperature of the gas falls and hence cooling takes place.
Question 19.
Why an engine working under isothermal conditions can produce no useful work?
Answer:
We know that
η = 1 – \(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}}\)
For the isothermal operation of the engine,
T1 = T2,
So η = 0
Hence an engine working under isothermal conditions can do no useful work.
Question 20.
What do you mean by internal energy?
Answer:
When work is done on the gas, it gets compressed and its temperature rises. The work done is converted into another form of energy called internal energy of the gas and the total energy remains conserved. The internal energy is chiefly the result of kinetic energy arising from the notion of the molecules inside the gas.
Question 21.
Why Cp is greater than Cv for a gas?
Answer:
When heat is given to a gas keeping its volume constant whole of it is used to raise the kinetic energy hence, the temperature of the gas. But if the pressure is to be kept constant, then an additional amount of heat is needed to raise the temperature of the same amount of gas by the same extent as the gas has to do work against pressure in the expansion (volume is now increased). Thus according to the definition of Cp and Cv, Cp>Cv.
Question 22.
Why a room cannot be cooled by leaving. the door of a refrigerator open?
Answer:
This room cannot be cooled because the refrigerator takes out heat from stuff kept inside the refrigerator and rejects it to the surroundings i.e. room.
Question 23.
Explain how heat can be added to a system without changing its temperature?
Answer:
if heat is added to a system to do only the external work, then there will be.no a rise in temperature.
Question 24.
Why a stove-pin does not burn one’s fingers even when its other end is red hot?
Answer:
This is because of the fact that the pin, has a very small area of cross-section, thus the amount of heat conducted which is directly proportional to the area of the cross-section is very small.
Question 25.
Although mechanical energy can be fully converted into heat energy, yet the reverse is not true? Why?
Answer:
This is because a part of heat energy is always retained by the system in the form of its internal energy.
Question 26.
How can a refrigerator be used as a heat pump to heat a room in winter?
Answer:
Install the refrigerator in a window such that its back is inside the room. The refrigerator will now reject the heat inside the room which will get warmed up.
Question 27.
What is the difference between the internal energy of an idea and a real gas?
Answer:
The internal energy of an ideal gas depends upon K.E only while for a real gas, it depends upon both K.E and P.E
Question 28.
Why can’t a Carnot engine be ever designed?
Answer:
It is because the conditions imposed on the source, sink, insulating stand, cylinder-piston, and the working substance can’t be achieved fully.
Question 29.
Air escaping from a cycle tube becomes cool on removing the value. Why?
Answer:
The air in a cycle tube is present at a present greater than the atmospheric pressure. When the valve is removed, the air expands suddenly i.e. adiabatic expansion takes place and the temperature decreases, thus the tube becomes cool.
Question 30.
Explain the need fofthesecbndiaWbf thermodynamics.
Answer:
Its need is as follows:
- The heat flows from a body at a higher temperature to a body at a lower temperature, but why not from a body at a lower temperature to a higher temperature.
- Heat engine converts heat into Work, but Why is the efficiency of an engine less than one?
- When we rotate a paddle in a beaker containing water, we know that the Work was done is converted into heat but when we put a paddle in hot water, no mechanical work is done. Why?
The above questions lead us to the need for the second law of thermodynamics.
Thermodynamics Important Extra Questions Long Answer Type
Question 1.
Discuss the Carnot cycle and give essential features of a Carnot engine.
Answer:
Carnot cycle: Heat engines essentially have
- a source of heat,
- a W0fkthg substance
- a sink (at a temperature lower than that source) and
- mechanical parts.
Carnot designed an idea engine that operated in the reversible cycle. The cycle consisted of two isotherms and two adiabatic. The heat was taken in or rejected during isothermal expansion or contraction. The Carnot cycle thus consists of four steps (see fig.) Carnot took a perfect gas as the working substance enclosed in a cylinder with perfectly insulting walls fitted with an insulating piston but the bases of the cylinder were conducting
(1) In the first step of the cycle let P1, V1, by the pressure of the gas. It is placed, in contact with the. source of heat at temperature T1 i.e the cylinder is out on the source. As the gas expands isothermally it absorbs some amount of heat to keep the temperature constant (curve AB)
The heat absorbed from the source Q1 is equal to the work done W, in expanding the gas volume from V1 to V2 at temperature T1 so that
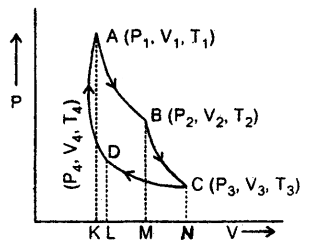
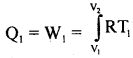
In = Area ABMKA ….(1)
(2) The cylinder is put on insulating and gas is allowed to expand from V2 to V3 adiabatically. Its temperature falls from T1 to T2 and pressure becomes P3 and P2. The work done W is then
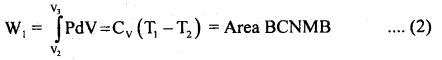
(3) In this part of the cycle the cylinder is put with its conducting base in contact with a sink as temperature T2 and gas is compressed isothermally. It rejects Q2 heat at constant temperature T2, the work done on the gas is [pressure volume change to (P4, V4) from (P3, V3)].
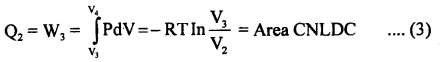
(4) In the last step of the cycle, the cylinder’s base is again put on the insulating stand, and the gas is compressed adiabatically so that the system returns back to its original state at A i.e. from (P4, V4) to (P1, V1) at temperature T1 via curve DA. Now the work done on the gas is
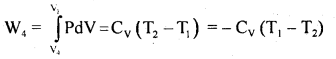
= Area DLKAD …. (4)
From equation (2) and (4), it is clear that W4 = W2
If W = net work done by the engine in one cycle, then
W = W1 + W2 + (- W3) + (- W4)
= W1 – W3 = Area ABCDA = Q1 – Q2 …..(5)
The efficiency of the Carnot engine (η): It is defined as the ratio of work done by the engine to the energy supplied to the engine in a cycle.
i.e η = \(\frac{\mathrm{W}}{\mathrm{Q}_{1}}=\frac{\mathrm{Q}_{1}-\mathrm{Q}_{2}}{\mathrm{Q}_{1}}\)
= 1 – \(\frac{\mathrm{Q}_{2}}{\mathrm{Q}_{1}}\)
Using equations (1) and (3)
\(\frac{Q_{1}}{Q_{2}}=\frac{R T_{1} l n \frac{V_{2}}{V_{1}}}{R T_{2} l n \frac{V_{3}}{V_{4}}}\) …(7)
Since B and C lie on the same adiabatic so
T1V2γ-1; = T2V3γ-1
or
\(\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}}=\left(\frac{\mathrm{V}_{3}}{\mathrm{~V}_{2}}\right)^{\gamma-1}\) ….(8)
Also D and A lie on the same adiabatic so
T1V1γ-1 = T2V4γ-1
or
\(\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}}=\left(\frac{\mathrm{V}_{4}}{\mathrm{~V}_{1}}\right)^{\gamma-1}\) ….(9)
∴ from (8) and (9), we get
\(\left(\frac{V_{3}}{V_{2}}\right)^{\gamma}\) = \(\left(\frac{V_{4}}{V_{1}}\right)^{\gamma}\)
ln \(\frac{\mathrm{V}_{3}}{\mathrm{~V}_{\mathrm{4}}}\) = ln \(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{\mathrm{1}}}\) …(10)
∴ from (7) and (10), we get
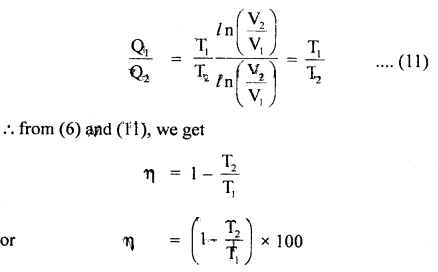
- The interesting aspect of η of Carnot engine is that it is independent of the nature of the working substance. But Carnot used an ideal gas operation which is not strictly followed by real gases or fuel
- Theoretically, η can be 100%.
- The efficiency of Carnot’s ideal engine depends only on the temperature of the scarce and the sink.
- The efficiency of any reversible engine working between the same two temperatures is the same.
Question 2.
Derive the expression for the work done during:
(a) Isothermal process
(b) Adiabatic process
Answer:
Consider one mole of a perfect gas contained in a cylinder having conducting walls and fitted with a movable piston.
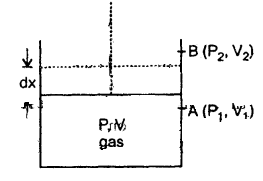
Let P, V be the pressure and volume of the gas corresponding to this state.
Let dx = distance by which piston moves outward at constant pressure P so that its volume increases by dV.
Let a = area of cross-section of the piston.
(a) If dW = work done in moving the piston by dx, then .
dW = force on piston × dx
= P a dx
= PdV …(i)
Where dV = a dx = volume
Let the system goes from initial state A(P1, V1) to final state B(P2, V2)
If W = total work done from A to B, then
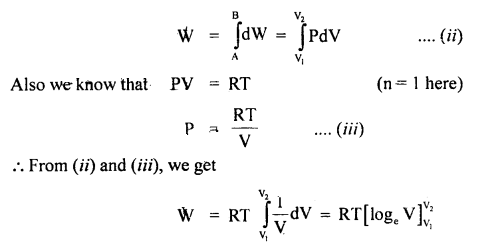
= RT (logeV2 – logeV1)
= RT log2 \(\frac{V_{2}}{V_{1}}\)
= 2.303 RT log10 \(\frac{V_{2}}{V_{1}}\)
(b) From equation (ii) of case (a), we get

We know that an adiabatic process is represented mathematically by the equation:
PVγ = constant = K
or
P = \(\frac{\mathrm{K}}{\mathrm{V}^{\gamma}}\) …(iii)
∴ from (ii) and (iii), we get
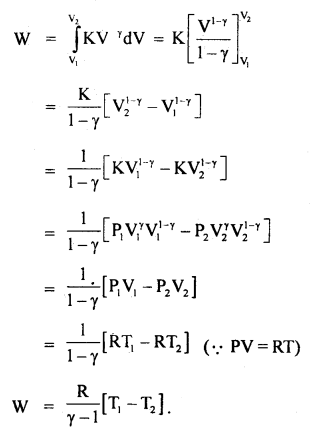
Numerical Problems:
Question 1.
A gas is suddenly compressed to 1/3 of its original volume. Calculate the rise in temperature, the original temperature being 300K and γ = 1.5.
Answer:
Let V1 = Initial volume
V2 = Final volume = \(\frac{\mathrm{V}_{1}}{3}\)
or
\(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}\) = 3
T1 = 300K
T2 – T1 = ?
γ = 1.5
We know that for an adiabatic change,
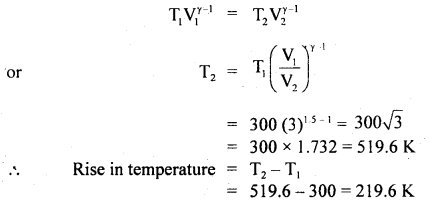
Question 2.
The efficiency of an ideal engine is \(\frac{1}{8}\). By lowering the temperature of the sink by 100 K, it increases to \(\frac{1}4}\). Find the initial and final temperature of the sink.
Answer:
Here, η1 = \(\frac{1}{8}\) in 1st case
η2 = \(\frac{1}{4}\) in 2nd case
Let T1 = Temperature of source
T2 = Initial Temperature of sink
and
T’2 = final Temperature of sink
= T2 – 100
∴ Using the relation

T1 = 800 K …(3)
from (1) and (3), we get
T2 = \(\frac{7}{8}\) × 800 = 700 K
∴ T’2 = 600 K
Question 3.
A perfect Qarjiotreiigifae utilizes an ideal gas. The source temperature is 500K and since the temperature is 375 K. If the engine takes 600 Kcal per cycle from the source, compute:
(a) the efficiency of The engine.
Answer:
Here, T1 = 50.0 K
T2 = 375 k
Q1 = Heat absorbed per cycle
= 600 K cal
∴ (a) Using t|ig relation,
η = 1 – \(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{\mathrm{1}}}\), we get
η = \(\frac{T_{1}-T_{2}}{T_{1}}=\frac{500-375}{500}\)
= \(\frac{125}{500}\) = 0.25
η% = 0.25 × 100 = 25%
(b) work done per cycle,
Answer:
Let W = work done per cycle
∴ Using relation
η = \(\frac{\mathrm{W}}{\mathrm{Q}_{1}}\), we get
W = ηQ1
= 0.25 × 600 K cal
= 150 K cal
= 150 × 103 × 4.2 J
= 6.3 × 105 J.
(c) heat rejected to the sink per cycle.
Answer:
Let Q2 = heat rejected to the sink
∴ Using the relation
W = Q1 – Q2, we get
Q2 = Q1 – W = 600 – 150 = 450 K cal
Question 4.
A refrigerator has, to transfer an average of 263 J of heat per second from temperature – 10°C to 25°C. Calculate the average power consumed assuming ideal reversible cycle and no other l0sses.
Answer:
Here, T1 = 25 + 273 = 298 K
T2 = – 10 + 273 = 263 K
Q2 = 263 Js-1
we know that
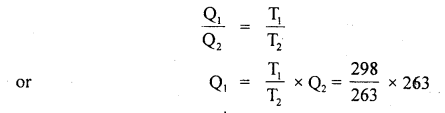
= 298 Js-1
∴ Average power consumed = Q1 – Q2
= (298 – 263) Js-1
= 35 W
Question 5.
Assuming the domestic refrigerator as a reversible engine working between the melting point of ice and the room temperature of 27°C, calculate the energy in Joule that must be supplied to freeze one kg of water. Given the temperature of water 0°C, L = 80 cal g-1.
Answer:
Here, T1 = 27 + 273 = 300 K
T2 = 0 + 273 = 273 K
m = 1 kg = 1000 g
L = 80 cal g-1
Heat to be removed, Q2 = mL
= 1000 × 80 cal
= 8 × 104 cal
Using the relation
\(\frac{\mathrm{Q}_{1}}{\mathrm{Q}_{2}}=\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}}\), we get
Q1 = \(\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}}\) × Q2 = \(\frac{300}{273}\) × 8 × 104
= 87912.1 cal
Energy required to be supplied,
W = Q1 – Q2
= (87912.1 – 80000) cal
= 7912.1 cal
= 7912.1 × 4.2 J
= 33230.8 J.
Question 6.
What is the coefficient of performance (β) of a Carnot refrigerator working between 30°C and 0°C?
Answer:
Here, T2 = 0°C = 273 K
T1 = 30°C = 273 + 30 = 303 K
β = ?
Using the relation,
β = \(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}-\mathrm{T}_{2}}\), we get
β = \(\frac{273}{303-273}=\frac{273}{30}\) = 9.1
Question 7.
A certain volume of dry air at NTP is allowed to expand 4 times its original volume under
(a) isothermal conditions
(b) adiabatic conditions.
Calculate the final pressure and temperature in each case γ = 1.4.
Answer:
Here, let V1 = V
∴ V2 = 4V
P1 = 76 cm of Hg
P2 = ?
γ = 1.4
T1 = 273 K
T2 = ?
(a) For isothermal expansion,
P1V1 = P2V2
or
P2 = P1\(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}\)
= \(\frac{76}{4}\) = 19 cm of Hg.
Since the process is isothermal, therefore the final temperature will be the same, as the initial temperature.
T1 = 273 K
(b) Adiabatic expansion Using the relation
P1V1γ = P2V2γ

Question 8.
A liter of hydrogen at 27°G and 106 dyne cm-2 pressure expands isothermally until its volume is doubled and then adiabatically until redoubledi’Find the final temperature, pressure and work done in each case, γ = 1.4
Answer:
Here, P1 = 106 dyne cm-2
V1 = 103 cm3 = 1 litre
T1 = 27 °C = 300 K.
V2 = 2V1
= 2000 cm3 for isothermal expansion
T2 =?
P2 =?
For adiabatic expansion
V1 = 2000 cm3
V’1 = 2V’1 = 4000 cm3
(a) For isothermal expansion: Using the relation
P2V2 = P1V1,we get
P2 = \(\frac{P_{1} V_{1}}{V_{2}}=\frac{10^{6} \times 10^{3}}{2 \times 10^{3}}\)
= 5 × 105 dyne cm-2
T2 = T1 for isothermal expansion = 300 K = 27°C
Work done during isothermal expansion is given by
W = 2.303 RT log10\(\left(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\right)\)
= 2.303 P1V1 log10\(\left(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\right)\)
= 2.303 × 106 × 103 log102
= 2.303 × 109 × 0.3010
= 6.93 × 108 erg
(b) For adiabatic expansion:

= – 45.6 °C
Work dorie during adiabatic expansion is given by
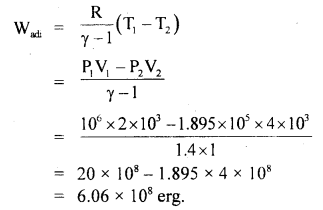
Question 9.
A 50g lead bullet (specific heat 0.02) is initially at 30°C. It is fired vertically upward with a speed of 840 ms-1. On returning to the starting level, it strikes a cake of ice at 0°C. How much ice is melted? Assume that all energy is spent in melting only. Latent heat of ice = 80 cal g-1.
Answer:
When bullet falls to the same level its velocity is same i.e. 840 ms-1.
K.E. of bullet on returning to the same level
= \(\frac{1}{2}\)mv2 = \(\frac{1}{2}\) × \(\frac{500}{1000}\) × (840)2
or
W = 17640 J
This K.E. will be converted into heat energy on striking the cake of ice.
∴ Heat produced Q is given by
Q = \(\frac{\mathrm{W}}{\mathrm{J}}=\frac{17640}{4.2}\) = 4200 cal
Heat given up by the bullet ih cooling to 0°C from 30°C is given by
Q2 = mcΔθ = 50 × 0.02 × 30
= 30 cal
∴ Total heat given to the ice = 4200 + 30 = 4230 cal
Let m = mass ice melted
∴ 4230 = mL
or
m = \(\frac{4230 \mathrm{cal}}{\mathrm{L}}=\frac{4230}{80 \mathrm{cal} \mathrm{g}^{1}}\)
or
m = 52.875 g.
Question 10.
Two moles of He gas (γ = \(\frac{5}{3}\)) J are initially at temperature 27°C and occupy a volume of 20 liters. The gas is first expanded at constant pressure until the volume is doubled. Then it undergoes an adiabatic change until the temperature returns to its initial value.
(a) Sketch the process on a P – V diagram.
(b) What are the final volume and pressure of the gas?
(c) What is the work done by the gas?
Answer:
Here, T1 = 27 + 273 = 300 K
V1 = 20 × 10-3 m-3
R = 8.3 J mol-1 K-1
n = 2
Using P1V1 = nRT1, we get
P1 = \(\frac{\mathrm{nRT}_{1}}{\mathrm{~V}_{1}}=\frac{2 \times 8.3 \times 300}{2 \times 10^{-2}}\)
= 24.9 × 104 = 2.49 × 105 Nm-2
Now when the gas is expanded at constant pressure, then let V2 and T2 be the new values of volume and temperature.
∴ According to Charle’s law
\(\frac{\mathrm{V}_{1}}{\mathrm{~T}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\)
Here, V1 = 2V1
∴ T2 = \(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\) × T1
= 2 × 300
= 600 K
∴ V2 = 2 × 2 × 10-2 = 4 × 10-2 m-3
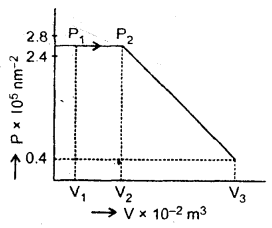
Finally gas expands adiabatically.
Let P3, V3, T3 be the new values of pressure, volume and temperature.
Here, T3 = T1 = 300 K

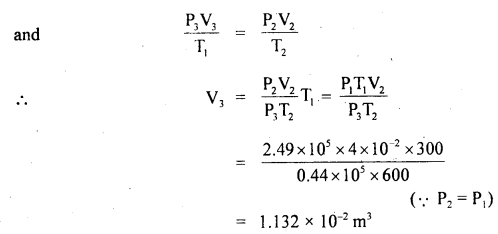
The process is shown in the figure:
Total work done (W) is given by
W = work done (W1) during expansion at constant pressure + work done (W2) during adiabatic expansion
or
W = W1 + W2
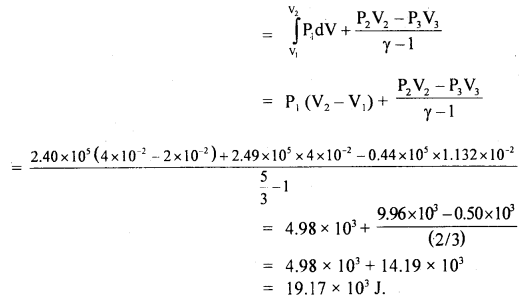
Question 11.
The motor in a refrigerator has a power output of 250 watts. The freezing compartment is at 270 K and outside air at 300 K. Assuming ideat efficiency, what is the amount of heat that can be extracted from the freezing compartment in 10 minutes? What is the shortest time in which 10 kg of water at 273 K can be converted into ¡ce? J = 4.2 × 10-3 J K ca-1.
Answer:
We know that β = \frac{\mathrm{Q}_{2}}{\mathrm{~W}}=\frac{\mathrm{Q}_{2}}{\mathrm{Q}_{1}-\mathrm{Q}_{2}}=\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}-\mathrm{T}_{2}}\(\)
Here, T1 = 300 K
T2 = 270 K
W = 250 W = 250 J s-1
Q =?
t =?
∴ Q2 = Wβ = W\(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}-\mathrm{T}_{2}}\)
= 250 × \(\frac{270}{300-270}\)
= 250 × \(\frac{270}{30}\)
= 2250 J s-1
(i) Let Q = heat extracted from the freezing compartment in 10 minutes = ?
∴ Q = Q2 × 10 min = 2250 × 10 × 60
= 1350000 J
= \(\frac{135 \times 10^{4}}{4.2 \times 10^{3}}\) K cal.
= 321.4 K cal.
(ii) Heat required to convert 1 Kg of water at 273 K into ice,
Q’ = m × L = 1 × 80 K cal = 80 × 4.2 × 103 J
Let Q’ be extracted in a time t.
∴ rate of extraction of heat from freezing compartment
= \(\frac{80 \times 4.2 \times 10^{3}}{\mathrm{t}}\) J s-1
This rate must be equal to Q2
i.e. 2250 = \(\frac{80 \times 4.2 \times 10^{3}}{\mathrm{t}}\)
= 149.33 s.
Question 12.
In a refrigerator, heat from inside at 277 K is transferred to a room at 300 K. How many joules of heat will be delivered to the room for each joule of electric energy consumed ideally
Answer:
Here, T2 = 277 K
T1 = 300 K
Q1 =?
W = 1 J
Using the relation
β = \(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}-\mathrm{T}_{2}}\), we get
β = \(\frac{277}{300-277}=\frac{277}{23}\) = 12.04
Also we know that
β = \(\frac{\mathrm{Q}_{2}}{\mathrm{~W}}=\frac{\mathrm{Q}_{2}}{\mathrm{l}}\)
or
β = Q2
∴ Q2 = 12.04 J
Now W = Q1 – Q2
or
Q1 = W + Q2
or
Total heat delivered to the room,
Q1 = 1 + 12.04 = 13.04 J.
Question 13.
A Carnot-type engine is designed to operate between 480 and 300 K. Assuming that the engine actually produces 1.2 K J of mechanical energy per kilo cal of heat absorbed, compare the actual efficiency with the theoretical maximum efficiency.
Answer:
Here, T1 = 480 K
T2 = 300 K
W = 1.2 K J
Q1 = heat absorbed =1 K cal = 4.2 K J
If ηa be its actual efficiency, then
ηa % = \(\frac{\text { Energy output }}{\text { Energy input }}\) × 100
= \(\frac{\mathrm{W}}{\mathrm{Q}_{1}}\) × 100
= \(\frac{1.2}{4.2}\) × 100 = 28.57%
Also, let ηm be its maximum theoretical efficiency,
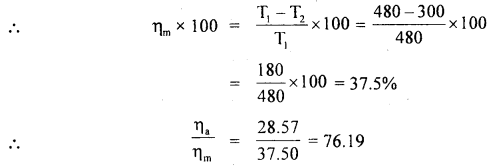
i.e. ηa is nearly \(\frac{3}{4}\) th of ηm.
Question 14.
20 m3 of a monoatomic gas at 12°C and pressure 100 K Pa is suddenly compressed to 0.5 m3. What are its new temperature and pressure? y for monoatomic gas = 1.67.
Answer:
Here, P1 = 100K Pa
V1 = 20m3
t1 = 12°C
∴ T1 = 273 + 12 = 285 K
γ = 1.67
V2 = 0.5 m3
= \(\frac{1}{2}\) m3
P2 =?
T2 =?
(a) Using the relation,
T1V1γ-1 = T2V2γ-1, we get
T2 = T1\(\left(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}\right)^{\gamma-1}\) = 285\(\left(\frac{20}{1 / 2}\right)^{167-1}\)
= 285 × (40)0.67
= 285 × 11.84
= 3374 K.
(b) Again using the relation
P1V1γ = P2V2γ, we get
P2 = P1\(\left(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}\right)^{\gamma}\)
= 100 × \(\left(\frac{20}{1 / 2}\right)^{1.67}\)
= 100 × (40)1.67
= 100 × 474
= 474 × 102 K Pa.
Question 15.
1 m3 of Helium originally at OC and 1 atmospheric pressure is cooled at constant pressure until the volume ¡s 0.75 m3. Calculate the heat removed. Sp. the heat of He = 3.1 KJ/kg K.
Answer:
Here, P1 = 1 atm = 1.013 × 105 Pa
V1 = 1 m3
T1 = 273 + 0 = 273 K
P2 = 1 atm
V2 = 0.75 m3 = \(\frac{3}{4}\) m3
Let T2 = final temperature
Cv = 3.1 KJ/kg K
∴ ΔV = (\(\frac{3}{4}\) – 1) m3
Using equation
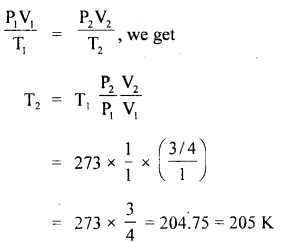
According to first law of thermodynamics,
ΔQ = ΔU + ΔW
For an idea gas, ΔU = μ Cv ΔT
ΔQ = μ Cv ΔT + PΔV
Also at S.T.P., one mole of a gas occupies a volume
= 22400 cc
or
1 Kmol = 22.4 m3
∴ 1 m3 volume contain = \(\frac{1}{22.4}\) K mol
∴ ΔQ = \(\frac{1}{22.4}\) × 3.1 (205 – 273) + \(\frac{1.013 \times 10^{5}(0.75-1)}{4184}\)
= – 9.11 – 6.05 × 10-5 × 105
= – 9.11 – 6.05
= – 15.2 K cal
Here – ve sign shows that heat is removed.
Question 16.
Determine the P – V relation for a monoatomic ideal gas undergoing an idiabatic process.
Answer:
For adiabatic process, 1st law of thermodynamics
dQ = dU + dW becomes
dU = – dW (∵ dQ = 0) …. (1)
The U for a monoatomic ideal gas is given by
U = \(\frac{3}{2}\) NkT
∴ dU = \(\frac{3}{2}\) NkdT …. (2)
Also dW = PdV ….(3)
Using (1), (2) and (3), we get
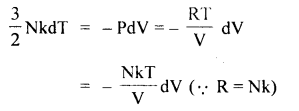
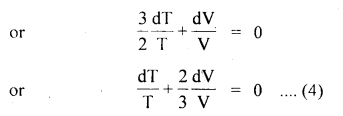
integrating equation (4), we get
log T + \(\frac{2}{3}\) logV = constant
or
log (TV2/3) = constant
or
TV2/3 = constant
In terms of P and V, PV5/3 = constant (∵ PV = RT)
Question 17.
The specific heat capacity of water is 4200 J/kg K. What is the change In the internal energy of 5 kg of water when it is heated from 20°G to 80°C?
Answer:
Here, C = 4200 J/kg K
m = 5 kg
T1 = 20°C + 273 = 293 K
T2 = 80 + 273 = 353 K
ΔT = T2 – T1
= 353 – 293 = 60 K
ΔU = ?
If ΔQ be the heat supplied to water for its heating, then using
ΔQ = mCΔT, we get
ΔQ = 5 × 4200 × 60
= 1260 KJ
Let us ignore the slight expansion in the volume of water,
∴ ΔW = PdV = 0
∴ ΔQ = ΔU + ΔW, gives
ΔU = ΔQ = 1260 KJ.
Question 18.
The specific heat of argon at constant pressure is 0.125 cal/gm and at constant volume is 0.075 cal g-1. Calculate the density of argon at N.T.P. J = 4.18 × 107 ergs ca-1 and normal pressure = 1.01 × 106 dynes cm-2.
Answer:
Here, Cp = 0.125 cal g-1
Cv = 0.075 cal g-1
J = 4.18 × 107 ergs cal-1
p = 1.01 × 106 dynes cm2
Cp – Cv = 0.125 – 0.075
= 0.050 cal g-1
Let ρ = density of argon at N.T.P. = ?
Using the relation,
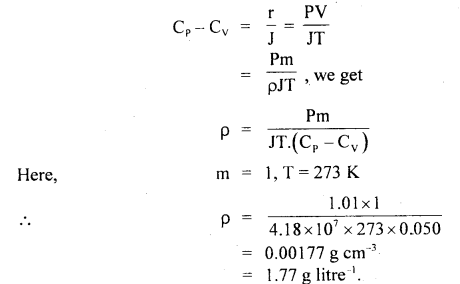
Question 19.
One gram of water at 373 K is converted into steam at the same temperature. Volume of 1 c.c. of water becomes 1671 cm3 on boiling. Calculate the change in internal energy of the system if heat of vaporization is 540 cal g-1. Atmospheric pressure is 1.013 × 105 Nm-2
Answer:
Here, m = mass of water = 1 g
V1 = initial volume = 1 cm3
V2 = final volume = 1671 cm3
P = atmospheric pressure = 1.013 × 105 Nm-2
L = heat of vaporization = 540 cal g-1
∴ dV = change in volume
= V2 – V1
= 1671 – 1 = 1670 cm3
= 1670 × 106 m3
∴ dW = PdV
= 1.013 × 105 × 1670 × 10-6 J
= 169.17 J
= \(\frac{169.17}{4.2}\) cal
= 40.3 cal
and dQ = mL = 1 × 540 cal
Let dU = change in internal energy of the system = ?
∴ According to first law of thermodynamics,
dQ = dU + dW
or
dU = dQ – dW
or
dU = mL – PdV
= 1 × 540 – 40.3
= 499.7 cal.
Question 20.
A perfect Carnot engine utilizes an ideal gas. The temperature of the source is 500 K and that of the sink is 375 K. If the k engine takes 600 Kcal per cycle from the source, then calculate:
Answer:
Here, T1 = temp, of source = 500 K
T2 = temp, of sink = 375 K
Q1 = heat absorbed from the source per cycle
= 600 Kcal
(i) the efficiency of the engine.
Answer:
Let η = thermal efficiency of the Carnot engine,
then η = \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{~T}_{1}}=\frac{500-375}{500}\)
= \(\frac{125}{500}\) = 0.25
∴ η = 0.25 × 100 = 25%
(ii) work done per cycle in Joule.
Answer:
Let W be the work done/cycle, then
η = \(\frac{\text { Work done per cycle }}{\text { Heat absorbed per cycle }}=\frac{\mathrm{W}}{\mathrm{Q}_{1}}\)
or
\(\frac{25}{100}=\frac{\mathrm{W}}{600}\)
or
W = 25 × 6 = 150 K cal
= 150 × 103 cal
= 150 × 103 × 4.2 J
= 6.3 × 105 J.
(iii) heat rejected to the sink per cycle.
Answer:
Let Q2 = heat rejected to the sink per cycle, then
Q1 = W + Q2
or
Q2 = Q1 – W
= 600 – 150
= 450 K cal.
Question 21.
A diatomic gas is heated at constant pressure. What fraction of the heat energy is used to increase the internal energy?
Answer:
Let ΔQ = heat given to the gas
ΔU = increase in the internal energy
ΔW = work done from first law of thermodynamics,
∴ from first law of thermodynamics,
ΔQ = ΔU + ΔW
For diatomic gas,
ΔQ = Cp ΔT
and ΔU = Cv ΔT
∴ \(\frac{\Delta U}{\Delta Q}=\frac{C_{V}}{C_{P}}=\frac{\frac{5}{2} R}{\frac{7}{2} R}=\frac{5}{7}\)
Question 22.
A gas is enclosed in a vessel of volume 1000 cc at a pressure of 72.6 cm of Hg. It is being evacuated with the help of a piston pump, which expels 10% gas in each stroke. What will be the pressure after the second stroke?
Answer:
Here, V0 = initial volume = 1000 cm3
P0 = initial pressure = 72.6 cm of Hg
\(\frac{\Delta \mathrm{V}}{\mathrm{V}_{0}}\) = rate of expelling the gas per stroke
= 10% = \(\frac{10}{100}=\frac{1}{10}\)
∴ After first stroke,
P1(V0 + ΔV) = P0V0
∴ After second stroke,
P2(V0 + ΔV) = P1V0
or
P2 = P0 \(\left(\frac{\mathrm{V}_{0}}{\mathrm{~V}_{0}+\Delta \mathrm{V}}\right)^{2}\)
= P0\(\left(\frac{1}{1+\frac{\Delta V}{V_{0}}}\right)^{2}\)
Where P1 and P2 are the pressures after first and second strokes.
∴ P2 = 72.6\(\left(\frac{1}{1+\frac{1}{10}}\right)^{2}\)
= 72.6 × \(\left(\frac{10}{11}\right)^{2}\)
= \(\frac{726}{10} \times \frac{100}{121}\)
= 60 cm of Hg.
Question 23.
A gas expands with temperature according to the relation V = kT2/3. What is the work done when the temperature changes by 30°C?
Answer:
Here, V = kT2/3
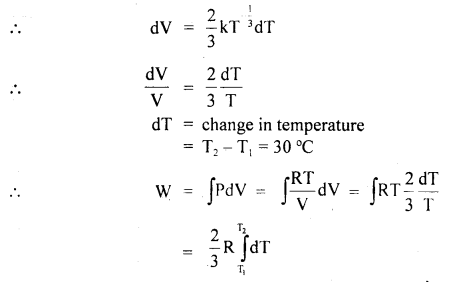
= R × \(\frac{2}{3}\)(T2 – T1)
= \(\frac{2}{3}\)R × 30 = 20 R.
Question 24.
A Carnot engine has the same efficiency when working:
(a) between 100 K and 500 K and
(b) between 180 K and T K.
Calculate the temperature T of the source in case (b).
Answer:
Here,
(a) T1 = temperature of source = 500 K
T2 = temperature of sink = 100 K
(b) T’1 = temperature of source = T K = ?
T’2 = temperature of sink = 180 K
Let η and η’ be the efficiency in case (a) and (b) respectively.
As η = η’ (given)
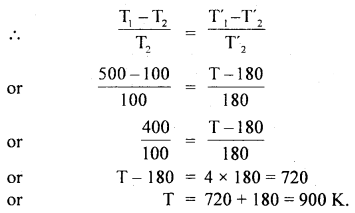
Question 25.
An ideal gas in a cylinder is compressed adiabatically to one-third of its original volume. During the process. 45 J of work is done on the gas by the compressing agent. By how much did the internal energy of the gas change in the process? How much heat flowed into the gas.
Answer:
Here, ΔQ = 0, ΔW = – 45 J, ΔU = ?
According to first law of thermodynamics,
ΔQ = ΔU + ΔW, we get
ΔU = 0 – ΔW
= – (- 45) = 45 J .
As the process is adiabatic, so the heat flow is zero.
Value-Based Type:
Question 1.
Amita who is a student of class XI asked a question to her friend Smita. Smita let me answer: Can you design a heat engine of 100% efficiency? Explain your answer. She was totally confused and did not able to answer it. Then, Amita explained it as under:
(i) Which value is displayed by Amita?
Answer:
The values displayed by Amita are:
(a) Helping nature
(b) Keen to share, her ideas
(c) Interested in teaching
(d) Co-operative.
(ii) How did she explain it?
Answer:
The efficiency of a heat engine is given by
η = 1 – \(\frac{T_{2}}{T_{1}}\)
The efficiency will be 100% or 1 if T2 = OK
Since these conditions cannot be attained practically.
So, a heat engine can not have 100% efficiency:
Question 2.
Sweta, a student of class XI asked her physics teacher “Can a room be cooled by opening the door of a refrigerator in a closed room?
Her teacher answered as under:
No, when a refrigerator is working in a closed room with its door closed, it is rejecting heat from inside to the air in the room. So the temperature of the room increases gradually.
When the door of the refrigerator is kept open, heat rejected by the refrigerator to the room will be more than the heat taken by the refrigerator from the room (by an amount equal to work done by the compressor). Therefore, the temperature of the room will increase at a slower rate compared to the first case.
(i) What values are displayed by Sweta?
Answer:
The values shown by Sweta are: Sharp mind, observing nature, awareness, scientific attitude.
(ii) Is there any case when the opening of the door of a refrigerator will cool the room gradually?
Answer:
Yes, if a heat-rejecting portion of the refrigerator is outside the closed room, then the opening of the refrigerator’s door will cool the room gradually.
(iii) A refrigerator is to remove heat from the eatable kept inside at 10°C. Calculate the coefficient of performance, if the room temperature is 36°C.
Answer:
Here, T1 = 36°C = (36 + 273) K = 309 K
T2 = 10°C = (10 + 273)K = 283K
Coefficient of performance = \(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}-\mathrm{T}_{2}}=\frac{283}{309-283}\)
= \(\frac{283}{26}\) = 10.9
Question 3.
Shikhar told his friend that the transfer of heat can not take place from a colder body to a holler body. His friend Raman was surprised as there were no such explanations in the first law of thermodynamics about the direction in which change can occur. Finally, they went to ask their physics teacher the reason behind it.
(i) What values are shown by them?
Answer:
The values shown by them are: Curiosity, Group Discussion, and keenness to know the scientific reason.
(ii) How did the teacher explain it?
Answer:
The teacher explained that this is the limitation of the first law of thermodynamics. However, heat transfer occurs from the body, at higher temperatures to lower temperatures. According to the second law of thermodynamics, ds ≥ 0 i.e system cannot move towards the direction of decreasing entropy/probability. Hence, heat cannot flow by itself from a colder body to a hotter body.