Kinetic Theory Class 11 Important Extra Questions Physics Chapter 13

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 13 Kinetic Theory. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 13 Important Extra Questions Kinetic Theory

Kinetic Theory Important Extra Questions Very Short Answer Type

Question 1.
What does gas constant R signify? What is its value?
Answer:
The universal gas constant (R) signifies the work done by (or on) a gas per mole per kelvin. Its value is 8.31 J mol^-1 K

Question 2.
What is the nature of the curve obtained when:
(a) Pressure versus reciprocal volume is plotted for an ideal gas at a constant temperature.
Answer:
It is a straight line.

(b) Volume of an ideal gas is plotted against its absolute temperature at constant pressure.
Answer:
It is a straight line.

Question 3.
The graph shows the variation of the product of PV with the pressure of the constant mass of three gases A, B and C. If all the changes are at a constant temperature, then which of the three gases is an ideal gas? Why?

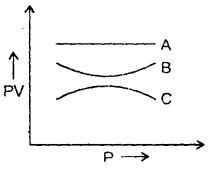
Answer:
A is an ideal gas because PV is constant at constant temperature for an ideal gas.

Question 4.
On the basis of Charle’s law, what is the minimum possible temperature?
Answer:
– 273.15°C.

Question 5.
What would be the ratio of initial and final pressures if the masses of all the molecules of a gas are halved and their speeds are doubled?
Answer:
1: 2 (∵ P = \(\frac{1}{3} \frac{\mathrm{mn}}{\mathrm{V}}\)C²)

Question 6.
Water solidifies into ice at 273 K. What happens to the K.E. of water molecules?
Answer:
It is partly converted into the binding energy of ice.

Question 7.
Name three gas laws that can be obtained from the gas equation.
Answer:

1. Boyle’s law
2. Charle’s law
3. Gay Lussac’s law.

Question 8.
What is the average velocity of the molecules of a gas in equilibrium?
Answer:
Zero.

An online Charles law calculator determines the value of initial temperature, final temperature, initial volume, final volume, pressure, ext…

Question 9.
A vessel is filled with a mixture of two different gases. Will the mean kinetic energies per molecule of both gases be equal? Why?
Answer:
Yes. This is because the mean K.E. per molecule i.e. \(\frac{3}{2}\) kT depends only upon the temperature.

Question 10.
Four molecules of a gas are having speeds, v₁, v₂, v₃ and v₄.
(a) What is their average speed?
Answer:
V_av = \(\frac{v_{1}+v_{2}+v_{3}+v_{4}}{4}\)

(b) What is the r.m.s. speed?
Answer:
V_rms = \(\sqrt{\frac{v_{1}^{2}+v_{2}^{2}+v_{3}^{2}+v_{4}^{2}}{4}}\)

Question 11.
The density of a gas is doubled, keeping all other factors unchanged. What will be the effect on the pressure of the gas?
Answer:
It will be doubled. (∵ P ∝ ρ if other factors are constant).

Question 12.
What is the average translational K.E. of an ideal gas molecule at a temperature T?
Answer:
\(\frac{3}{2}\) kT, where k is Boltzmann Constant.

Question 13.
Define the mean free path of a molecule.
Answer:
It is defined as the average distance travelled by a molecule between two successive collisions.

Question 14.
At what temperature, Charle’s law breaks down?
Answer:
At very low temperature, Charle’s law breaks down.

Question 15.
A container has an equal number of molecules of hydrogen and carbon dioxide. If a fine hole is made in the container, then which of the two gases shall leak out rapidly?
Answer:
Hydrogen would leak faster as r.m.s. speed of hydrogen is greater than the r.m.s. speed of CO₂.

Question 16.
Two different gases have the same temperature. Can we conclude that the r.m.s? velocities of the gas molecules are also the same? Why?
Answer:
No. If temperature is same, then \(\frac{3}{2}\) kT is same. Also \(\frac{1}{2}\) mC² is same. But m is different for different gases. C will be different.

Question 17.
A gas enclosed in a container is heated up. What is the effect on pressure?
Answer:
The pressure of the gas increases.

Question 18.
What is an ideal gas?
Answer:
It is a gas in which intermolecular forces are absent and it obeys gas laws.

Question 19.
Define absolute zero.
Answer:
It is defined as the temperature at which all molecular motions cease.

Question 20.
What do you understand by the term ‘Collision frequency’?
Answer:
It is the number of collisions suffered by a molecule in one second.

Question 21.
What do you understand by the term ‘mean free path’ of a molecule?
Answer:
It is the average distance travelled by the molecule between two successive collisions.

Question 22.
Mention two conditions when real gases obey the ideal gas equation PV = RT?
Answer:
Low pressure and high temperature.

Question 23.
Comment on the use of water as a coolant.
Answer:
Since water has a high value of specific heat so it can be used as a coolant.

Question 24.
Do Water and ice have the same specific heats? Why water bottles are used for fomentation?
Answer:
No. For water C = 1 cal g^-1 °C^-1 for ice, C = 0.5 cal g^-1°C^-1. It is because water has a high value of specific heat.

Question 25.
(a) What is the value of γ for a monoatomic and a diatomic gas?
Answer:
γ is 1.67 and 1.4 for monoatomic and diatomic gas respectively.

(b) Does the value of y depend upon the atomicity of the gas?
Answer:
Yes.

Question 26.
Which of the two has larger specific heat-monoatomic or diatomic gas at room temperature?
Answer:
Diatomic gas has more specific heat than a monoatomic gas e.g. Molar specific heat at constant volume is \(\frac{5}{2}\)R for monoatomic gas and \(\frac{5}{2}\)R for diatomic gas.

Question 27.
What is the effect on the pressure of an if it is compressed at constant temperature?
Answer:
Applying Boyle’s law, we find that the pressure increases.

Question 28.
What is the volume of a gas at absolute zero of temperature?
Answer:
Zero.

Question 29.
Why the pressure of a gas enclosed in a container increases on heating?
Answer:
This is because the pressure of a gas is proportional to the absolute ‘ temperature of the gas if V is constant.

Question 30.
The number of molecules in a container is doubled. What will be the effect on the r.m.s? speed of Slit molecules?
Answer:
No effect.

Question 31.
What will be the effect on K.E. and pressure of the gas in the above quation?
Answer:
Both will be doubled.

Question 32.
Does real gases obey the gas equation, PV = nRT.
Answer:
No.

Question 33.
On what factors does the internal energy of a real gas depend?
Answer:
It depends upon the temperature, pressure and volume of the gas.

Question 34.
What is the pressure of an ideal gas at absolute zero i.e. 0 K or – 273°C.
Answer:
Zero.

Question 35.
What do NTP and STP mean?
Answer:
They refer to a temperature of 273 K or 0°C and 1 atmospheric pressure.

Question 36.
What is the internal energy or molecular energy of an ideal gas at absolute zero?
Answer:
Zero.

Question 37.
Name the temperature at which all real gases get liquified?
Answer:
All real gases get liquified before reaching absolute zero.

Question 38.
Is the internal energy of the real gases sera at the absolute temperature?
Answer:
No.

Kinetic Theory Important Extra Questions Short Answer Type

Question 1.
Why cooling is caused by evaporation?
Answer:
Evaporation occurs on account of faster molecules escaping from the surface of the liquid. The liquid is therefore left with molecules having lower speeds. The decrease in the average speed of molecules results in lowering the temperature and hence cooling is caused.

Question 2.
On reducing the volume of the gas at a constant temperature, the pressure of the gas increases. Explain on the basis of the kinetic theory of gases.
Answer:
On reducing the volume, the space for the given number of molecules of the gas decreases i.e. no. of molecules per unit volume increases. As a result of which more molecules collide with the walls of the vessel per second and hence a larger momentum is transferred to the walls per second. Due to which the pressure of gas increases.

Question 3.
Why temperature less than absolute zero is not possible?
Answer:
According to the kinetic interpretation of temperature, absolute temperature means the kinetic energy of molecules.

As heat is taken out, the temperature falls and hence velocity decreases. At absolute zero, the velocity of the molecules becomes zero i.e. kinetic energy becomes zero. So no more decrease in K.E. is possible, hence temperature cannot fall further.

Question 4.
There are n molecules of a gas in a container. If the number of molecules is increased to 2n, what will be:
(a) the pressure of the gas.
(b) the total energy of the gas.
(c) r.m.s. speed of the gas molecules.
Answer:
(a) We know that
P = \(\frac{1}{3}\)mnC².
where n = no. of molecules per unit volume.
Thus when no. of molecules is increased from n to 2n, no. of molecules per unit volume (n) will increase from n 2n
\(\frac{n}{V}\) to \(\frac{2n}{V}\), hence pressure will become double.

(b) The K.E. of a gas molecule is,
\(\frac{1}{2}\)mC² = \(\frac{3}{2}\)kT
If the no. of molecules is increased from n to 2n. There is no effect on the average K.E. of a gas molecule, but the total energy is doubled.

r.m.s speed of gas is C_rms = \(\sqrt{\frac{3 \mathrm{P}}{\rho}}=\sqrt{\frac{3 \mathrm{P}}{\mathrm{mn}}}\)

When n ¡s increased from n to 2n. both n and P become double and the ratio \(\frac{P}{n}\) remains unchanged. So there will be no effect of increasing the number of molecule from n to 2n on r.m.s. speed of gas molecule.

Question 5.
Equal masses of O₂ and He gases are supplied equal amounts of heat. Which gas will undergo a greater temperature rise and why?
Answer:
Helium is monoatomic while O₂ is diatomic. In the case of helium, the supplied heat has to increase only the translational K.E. of the gas molecules.

On the other hand, in the case of oxygen, the supplied heat has to increase the translations, vibrational and rotational K.E. of gas molecules. Thus helium would undergo a greater temperature rise.

Question 6.
Two bodies of specific heats S₁ and S₂ having the same heat capacities are combined to form a single composite body. What is the specific heat of the composite body?
Answer:
Let m₁ and m₂ be the masses of two bodies having heat capacities S₁ and S₁  respectively.
∴ (m₁ + m₂)S = m₁S₁ + m₂S₂ = m₁S₁ + m₁S₁ = 2m₁S₁

S = \(\frac{2 m_{1} S_{1}}{m_{1}+m_{2}}\).

Also, m₂S₂ = m₁S₁
( ∵ Heat capacities of two bodies are same.)
or
m₂ = \(\frac{\mathrm{m}_{1} \mathrm{~S}_{1}}{\mathrm{~S}_{2}}\)

∴ S = \(\frac{2 \mathrm{~m}_{1} \mathrm{~S}_{1}}{\mathrm{~m}_{1}+\frac{\mathrm{m}_{1} \mathrm{~S}_{1}}{\mathrm{~S}_{2}}}=\frac{2 \mathrm{~S}_{1} \mathrm{~S}_{2}}{\mathrm{~S}_{1}+\mathrm{S}_{2}}\)

Question 7.
Tell the degree of freedom of:
(a) Monoatomic gas moles.
Answer:
A monoatomic gas possesses 3 translational degrees of freedom for each molecule.

(b) Diatomic gas moles.
Answer:
A diatomic gas molecule has 5 degrees of freedom including 3 translational and 2 rotational degrees of freedom.

(c) Polyatomic gas moles.
Answer:
The polyatomic gas molecule has 6 degrees of freedom (3 translational and 3 rotational).

Question 8.
State law of equipartition of energy.
Answer:
It states that in equilibrium, the total energy of the system is divided equally in all possible energy modes with each mode i.e. degree of freedom having an average energy equal to \(\frac{1}{2}\) k_BT.

Question 9.
Explain why it is not possible to increase the temperature of gas while keeping its volume and pressure constant?
Answer:
It is not possible to increase the temperature of a gas keeping volume and pressure constant can be explained as follows:

According to the Kinetic Theory of gases,

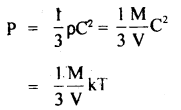
( ∵ C² = kT, when k is a constant)
T ∝ PV

Now as T is directly proportional to th^ product of P and V. If P and V are constant, then T is also constant.

Question 10.
A glass of water is stirred and then allowed to stand until the water stops moving. What has happened to the K.E. of the moving water?
Answer:
The K.E. of moving water is dissipated into internal energy. The temperature of water thus increases.

Question 11.
Why the pressure of a gas increases when it is heated up?
Answer:
This is due to the two reasons:

1. The gas molecules move faster than before on heating and so strike the container walls more often.
2. Each impact yields greater momentum to the walls.

Question 12.
R.m.s. velocities of gas molecules are comparable to those of a single bullet, yet a gas takes several seconds to diffuse through a room. Explain why?
Answer:
Gas molecules collide with one another with a very high frequency. Therefore, a molecule moves along a random and long path to go from one point to another. Hence gas takes several seconds to go from one comer of the room to the other.

Question 13.
Calculate the value of the universal gas constant (R).
Answer:
We know that R is given by
R = \(\frac{PV}{T}\)

Now one mole of all gases at S.T.P. occupy 22.4 litrês.
P = 0.76 m of Hg
= 0.76 × 13.6 × 10³ × 9.8
= 1.013 × 10⁵ Nm^-2

V = 22.4 litre
= 22.4 × 10 3m³

T = 273 K .
n = 1

∴ R = \(\frac{1.013 \times 10^{5} \times 22.4}{273}\) × 10^-3
= 8.31 J mol^-1 k^-1

Question 14.
Define and derive an expression for the mean free path.
Answer:
It is defined as the average distance travelled by a gas molecule between two successive collisions. It is denoted by X.

Derivation of Expression – Let us assume that only one molecule is in motion and all other molecules are at rest. ,
Let d = diameter of each molecule.
l = distance travelled by the moving molecule.

The moving molecule will collide with all those molecules whose centres lie inside a volume πd2l.
Let n = no. of molecules per unit volume in the gas.

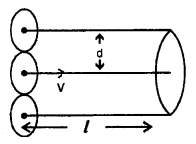
Now λ = \(\frac{\text { distance travelled }}{\text { no. of collisions }}=\frac{l}{\mathrm{n} \pi \mathrm{d}^{2} l}\)
or
λ = \(\frac{1}{n \pi d^{2}}\) …(1)

In this derivation, we have assumed that all but one molecules are at rest. But this assumption is not correct. All the molecules are in random motion. So the chances of a collision by a molecule are greater.

Thus taking it into account, the mean free path can be shown to be \(\sqrt{2}\) times less than that in equation (1),
∴ λ = \(\frac{1}{\sqrt{2} n \pi d^{2}}\)
which is the required expression.

Question 15.
On what parameters does the λ (mean free path) depends?
Answer:
we know that λ = \(\frac{\mathrm{k} \mathrm{T}}{\sqrt{2} \pi \mathrm{d}^{2} \rho}=\frac{\mathrm{m}}{\sqrt{2} \pi \mathrm{d}^{2} \rho}\)

= \(\frac{1}{\sqrt{2} \pi \mathrm{nd}^{2}}\)
∴ λ depends upon:

1. diameter (d) of the molecule, smaller the ‘d’, larger is the mean free path λ,.
2. λ ∝ T i.e. higher the temperature, larger is the λ.
3. λ ∝ \(\frac{1}{P}\) i.e. smaller the pressure, larger is the λ.
4. λ ∝ \(\frac{1}{ρ}\) i.e. smaller the density (ρ), larger will he the X.
5. λ ∝ \(\frac{1}{n}\) i.e. smaller the number of molecules per unit volume of the gas, larger is the λ.

Question 16.
What causes the Maxwellian distribution of molecular speed?
Answer:
Maxwellian distribution of molecular speed is a statistical phenomenon due to the intermolecular collisions in which the system tends to acquire equilibrium.

Question 17.
Why the pressure of a gas increases on increasing the temperature at constant volume?
Answer:
We know that C_rms ∝ \(\sqrt{T}\).

Thus when T is increased, the root means square velocity of gas molecules also increases, thus they move faster and the number of collisions per second with the walls of the container increase and thus pressure increases.

Question 18.
Explain why the temperature of a gas rises when it is compressed?
Answer:
The work is done against pressure during the compression and the velocity of the individual molecules increases, so their K..E. is increased and thus the temperature of the gas is increased.

Question 19.
What determines the average speeds of the molecules of the gases?
Answer:
The average speed of the molecules of the gases depends upon their mass and temperature.

Question 20.
What is the average velocity of the molecules of an ideal gas? Why?
Answer:
The average velocity of the molecules of an ideal gas is zero because the molecules possess all sorts of velocities in all possible directions. Thus their vector sum and hence average value is zero.

Question 21.
A person putting on wet clothes may catch cold-Why?
Answer:
The water in the clothes evaporates. The heat required for evaporation is taken from the body of the person wearing wet clothes. So due to the cooling of the body, he may catch a cold.

Question 22.
At what temperature the molecular speed of the gas molecules should reduce to zero? Does it really happen? Why?
Answer:
The molecular speed should reduce to zero at absolute zero. But such a situation never arises because all gases liquefy before that temperature is attained.

Question 23.
The temperature of the gas in Kelvin is made 9 times. How does it affect the total K.E., average K.E., r.m.s? velocity and pressure?
Answer:
Total K.E., average K.E. and pressure become 9 times, but the RMS velocity is tripled.

Question 24.
Do diatomic molecules have all types of motions? Explain.
Answer:
No. At very low temperature, they have only translatory r motion. At moderate temperature, they possess both translatory and rotatory motion and at very high temperature, all three types of motions are possible.

Question 25.
Why the molecules of an ideal monoatomic gas have only three degrees of freedom?
Answer:
It is so because the molecules of an ideal gas are point masses, so rotational motions are not significant. Thus it can have only three degrees of freedom corresponding to the translatory motion.

Question 26.
The adiabatic expansion causes a lowering of the temperature of the gas. Why?
Answer:
As the gas expands work needs to be done by the gas. The process being adiabatic, no heat is absorbed by the gas from outside, so the energy for doing work is obtained from the gas itself and hence its temperature falls.

Question 27.
What are the different ways of increasing the number of molecular collisions per unit time against the walls of the vessel containing a gas?
Answer:
The number of collisions per unit time .an be increased in the following ways:

1. By increasing the temperature of the gas.
2. By increasing the number of molecules.
3. By decreasing the volume of the gas,

Question 28.
Two identical cylinders contain helium at 2 atmospheres and argon at 1 atmosphere respectively. If both the gases are filled in one of the cylinders, then:
(a) What would be the pressure?
Answer:
(2 + 1) = 3 atmosphere.

(b) Will the average translational K.E. per molecule of both gases be equal?
Answer:
Yes, because the average translational K.E./molecule (\(\frac{3}{2}\)kT) depends only upon the temperature.

(c) Will the r.m.s. velocities are different?
Answer:
Yes, because of the r.m.s. velocity depends not only upon temperature but also upon the mass.

Question 29.
Why hydrogen escapes more rapidly than oxygen from the earth’s surface?
Answer:
We know that C_rms ∝ \(\frac{1}{\sqrt{\rho}}\)

Also ρ₀ = 16 ρ_H. So C_rms of hydrogen is four times that of oxygen at a given temperature. So the number of hydrogen molecules whose velocity exceeds the escape velocity from earth (11.2 km s^-1) is greater than the no. of oxygen molecules. Thus hydrogen escapes from the earth’s surface more rapidly than oxygen.

Question 30.
When a gas is heated, its molecules move apart. Does it increase the P.E. or K.E. of the molecules? Explain.
Answer:
It increases the K.E. of the molecules. Because on heating, the temperature increases and hence the average velocity of the molecules also increases which increases the K.E.

Question 31.
Distinguish between the terms evaporation, boiling and vaporisation.
Answer:
Evaporation: It is defined as the process of conversion of the liquid to a vapour state at all temperatures and occurs only at the surface of the liquid.

Boiling: It is the process of rapid conversion of the liquid to a vapour state at a definite temperature and occurs throughout the liquid.

Vaporisation: It is the general term for the conversion of liquid to vapour state. It includes both evaporation and boiling.

Kinetic Theory Important Extra Questions Long Answer Type

Question 1.
Derive gas laws from the kinetic theory of gases.
Answer:
(a) Boyle’s law: It states that P ∝ \(\frac{1}{V}\) if T = constant.
Derivation: We know from the kinetic theory of gases that

Here R = constant
If T = constant, then PV = constant
or
P ∝ \(\frac{1}{V}\).

(b) Charles’ law: It states that for a given mass of a gas, the volume of the gas is directly proportional to the absolute temperature of the gas if pressure is constant
i. e. V ∝ T.

Derivation: We know that
PV = \(\frac{1}{3}\)MC2= \(\frac{1}{3}\)mNC2
where N = Avogadro’s no.

Also, we know that mean K..E. of a molecule is

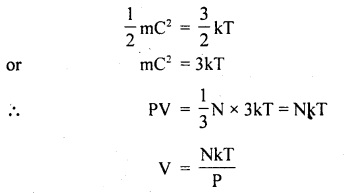
If P = constant, then V ∝ T. Hence proved.

(c) Avogadro’s Hypothesis: It states that equal volumes of all gases contain equal no. molecules if T and P are the same.

Derivation: Consider two gases A and B having n, and n2 as the no. of molecules, C₁ and C₂ are the r.m.s. velocities of these molecules respectively.

According to the kinetic theory of gases,

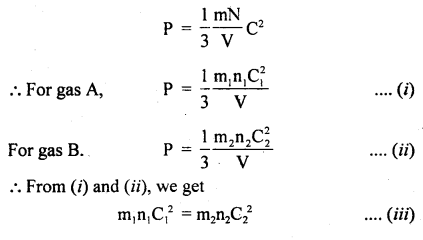
Also, we know that

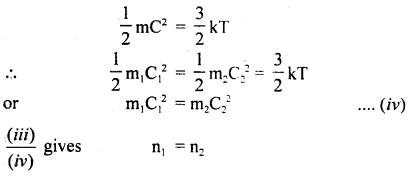
Hence proved.

(d) Graham’s law of diffusion of gases: It states that the rate of diffusion of a gas is inversely proportional to the square root of the density of the gas.
Derivation: We know that

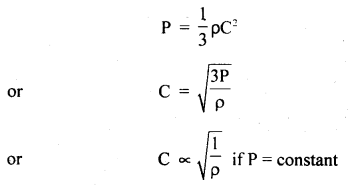
Also, we know that r.m.s. velocity is directly proportional to the rate of diffusion (r) of the gas, i.e.

Numerical Problems:

Question 1.
Calculate r.m.s. the velocity of hydrogen at N.T.P. Given the density of hydrogen = 0.09 kg m⁴.
Answer:

Question 2.
Calculate the temperature at which r.m.s. the velocity of the gas molecule is double its value at 27°C, the pressure of the gas remaining the same.
Answer:
Let t be the required temperature = ? and Ct, C27 be the r.m.s. velocities of the gas molecules at t°C and 27°C respectively.
\(\frac{\mathrm{C}_{\mathrm{t}}}{\mathrm{C}_{27}}\) = 2 (given)
Also let M = molecular weight of the gas
Now T = t + 273
and T₂₇ = 27 + 273 = 300 K

∴ Using the relation

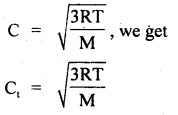
Question 3.
Calculate the K.E./mole of a gas at N.T.P. Density of gas at N.T.P. = 0.178 g dm^-3 and molecular weight = 4.
Answer:
Here, ρ = 0.178 g dm^-3
= 0.178 × 10^-3 g cm^-3 (∵ 1 dm³ = 10^-3 cm³)
= 178 × 10^-6 g cm^-3

Volume of 1 mole of gas i.e. 4 g of gas = \(\frac{\text { Mass }}{\text { Density }}\)

Question 4.
Calculate the diameter of a molecule if n = 2.79 × 10²⁵ molecules per m3 and mean free path = 2.2 × 10^-8 m.
Answer:
Here, n = 2.79 × 10²⁵ molecules m^-3
λ = 2.2 × 10^-8 m
d = ?

Using the relation.

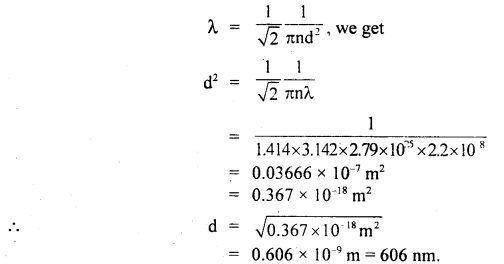
Question 5.
Calculate the number of molecules in 1 cm3 of a perfect gas at 27°C and at a pressure of 10 mm ofHg. Mean K.E. of a molecule at 27°C = 4 × 10²⁵ J. ρ_Hg = 13.6 × 103 kg m^-3.
Answer:
Here, K..E. per molecule at 27°C = 4 × 10^-11 J
Let μ = number of molecules in 1 cm³ or 10^-6 m³
∴ Mean K.E. per cm3 = μ × 4 × 10¹¹ J ….(i)
Now K.E. per gram molecule = \(\frac{3}{2}\) RT
for a perfect gas, PV = RT

∴ K.E, per gram molecule = \(\frac{3}{2}\) PV
or
K.E. per cm3 of gas = \(\frac{3}{2}\) PV
P = 10 mm of Hg = 10^-2 m of Hg
= 10^-2 × 13.6 × 10³ × 9.8
= 136 × 9.8 Nm^-2 V
= 1 cm³
= 10^-6 m³

∴ K.E per cm3 of gas = \(\frac{3}{2}\) × 136 × 9.8 × 10⁶
= 1.969 × 10^-3 J ….(ii)

∴ from (i) and (ii) we get
μ × 4 × 10^-11 = 1.969 × 10^-3
or
μ = \(\frac{1.969 \times 10^{-3}}{4 \times 10^{11}}\)
= 4.92 × 10⁷ molecules

Question 6.
Gas at 27°C ¡n a cylinder has a volume of 4 litres and pressure 1oo Nm².
(a) Gas is first compressed at a constant temperature so that the pressure is 150 Nm². Calculate the change in volume.
Answer:
Here, V₁ = 4 litres = 4 × 10^-3 m³
P₁ = 100 Nm^-2
P₂ = 150 Nm^-2
V₂ =?
T₁ = 273 + 27 = 300 K

∴ According to Boyle’s Law
P₁V₁ = P₂V₂
or
V₂ = \(\frac{P_{1} V_{1}}{P_{2}}=\frac{100 \times 4}{150}\) × 10^-3
= 2.667 × 10^-3 m³
= 2.667 litre.

∴ Change in volume = V₁ – V₂
= 4 – 2.667 = 1.333 litre.

(b) It is then heated at a constant volume so that temperature becomes 127°C. Calculate the new pressure.
Answer:
T₁ = 300 K
T₂ = 273 + 127 = 400 K
P₁ = 150 Nm^-2
P₂ = ?

At constant volume, according to Gay Lussac’s law

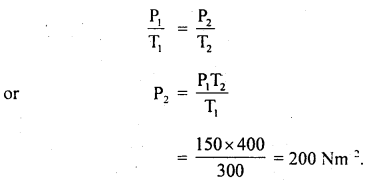
Question 7.
The temperature of a gas is – 68°C. To what temperature should it be heated so that
(a) the average K.E. of the molecules be doubled.
(b) the root mean square velocity of the molecules to be doubled?
Answer:
(a) Let θ°C be the temperature of gas up to which it is heated.
∴ T₂ = 273 + θ.
and T₁ = 273 + (- 68)
Let E₂ and E₁ be the average K.E. of the molecules at T₂ and T₁ respectively.

According to the given condition
\(\frac{\mathrm{E}_{2}}{\mathrm{E}_{1}}\) = 2

Using the relation,

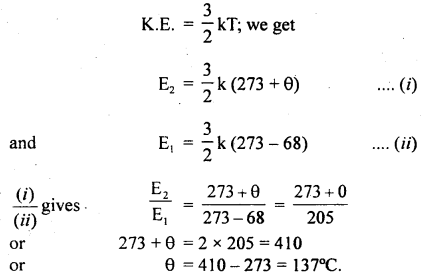
(b) Let t°C be the temperature up to which the gas is heated.
∴ T₃ = 273 + t
and T₄ = 273 – 68 = 205 K

Let C₁ and C₂ be the respective r.m.s. velocities of the molecules.
∴ \(\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}\) = 2 (given)

Now using the relation

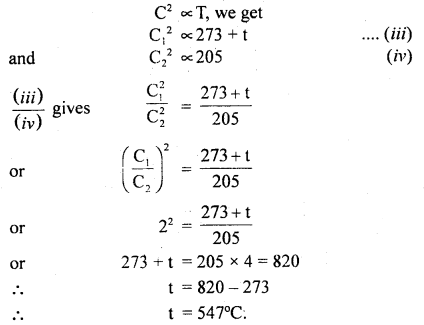
Question 8.
A balloon contains 500 m³ of He at 27°C and I atm pressure. Find the volume of the helium at 3°C and 0.5 atm pressure?
Answer:
Here, P₁ = 1 atm
T₁ = 27°C = 273 + 27 = 300 K
V₁ = 500 m3
P₂ = 0.5 atm
V₂ = ?
T₂ = – 3°C = 273 – 3 = 270

Using ideal gas equation,
PV = RT, we get
P₁V₁ = RT₁ …(i)
and P₂V₂ = RT₂ …(ii)

Dividing (i) by (ii), we get

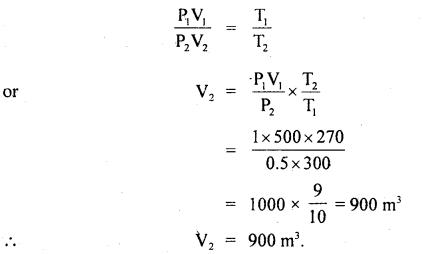
Question 9.
At what temperature will the average velocity of O₂ molecules be sufficient so as to escape from earth? V_e = 11.0 km s^-1 and mass of one molecule of O₂ is 5.34 × 10^-26 kg, k = 1.38 × 10^-23 JK^-1.
Answer:
Here, escape velocity from earth surface,
V_e = 11.0 kms^-1
= 11 × 10^-3 ms^-1
k = 1.38 × 10^-23 JK^-1

Mass of one O₂ molecule, M = 5.34 × 10^-26 kg
T = ?
We know that K.E. per molecule is given by

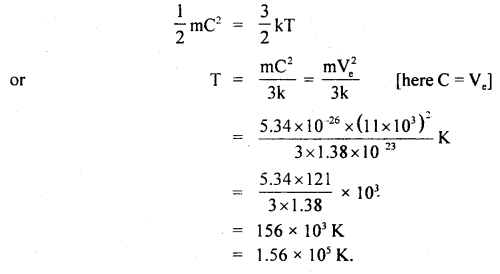
Question 10.
The volume of the air bubble increases 15 times when it rises from the bottom to the top of a lake. Calculate the depth of the lake if the density of lake water is 1.02 × 10³ kg m^-3 and atmospheric pressure is 75 cm of Hg.
Answer:
Here, P₁ = 75 cm of Hg
= 0.75 × 13.6 × 10³ × 9.8 Nm^-2
= 99.96 × 10³ Nm^-2

Let V₂ = volume of bubble at depth h = x
i.e. V₁ = x + 15x = 16x
P₂ = 0.75 m of Hg = hρ_water g
= 99.96 × 10³ + h × 10³ × 9.8

Using Byole’s law,
P₁V₁ = P₂V₂, we get
99.96 × 10³ × 16x = (99.96 × 10³ + h × 10³ × 9.8)x
or
h = \(\frac{15 \times 99.96 \times 10^{3}}{9.8 \times 10^{3}}\) = 153 m.

Question 11.
Two glass bulbs of volumes 500 cm³ and 100 cm³ are connected by a narrow tube of negligible volume. When the apparatus is sealed off, the pressure of the air inside is 70 cm of Hg and temperature 20°C. What does the pressure become if a 100 cm³ bulb is kept at 20°C and the other bulb is heated to 100°C?
Answer:
Here, V₂ = 500 cm³
V₁ = 100 cm³
P₁ = P₂ = P = ?
T₁ = 20°C = 293 K
T₂ = 100°C = 373 K
T = 20°C = 293 K
P’ = 70 cm of Hg

For a given mass of the gas,

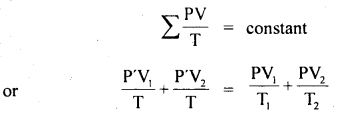
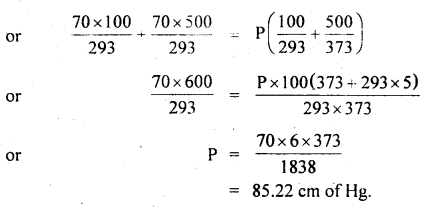
Question 12.
0.014 kg of nitrogen is enclosed in a vessel at a temperature of 27°C. How much heat has to be transferred to the gas to double the r.m.s. the velocity of its molecules?
Answer:
V_rms = \(\sqrt{\frac{3 R T}{M}}\)
Here, T₁ = 273 + 27 = 300 K .

Now to double the r.m.s. velocity, the temperature should be raised to four times the initial temperature.
i.e. T₂ = 4T, = 4 × 300 K = 1200 K
∴ ΔT = rise in temperature = T₂ – T₁
= 1200 – 300 – 900 K

k = 1.38 × 10-23 Jk^-1
C_v = \(\frac{5}{2}\) R = \(\frac{5}{2}\)(kN)
= \(\frac{5}{2}\) × 1.38 × 10^-23 × 6.023 × 10²³
= 20.8 JK^-1 mol^-1 …(i)

∴ If Δθ be the amount of heat required,
Then Δθ = n Cv ΔT
where n = number of moles of nitrogen in 0.014 kg
= \(\frac{1}{0.028}\) × 0.014
= \(\frac{1}{2}\) (∵ 1 mole of N₂ = 0.028 Kg)

∴ Δθ = \(\frac{1}{2}\) × 20.8 × 900
= 9360 J.

Question 13.
Four molecules of a gas have speeds 4,6,8 and 10 Km s^-1 respectively. Calculate their rms speed.
Answer:
Here, C₁ = 4 km s^-1
C₂ = 6 km s^-1
C₃ = 8 km s^-1
C₄ = 10 km s^-1
C = rms speed = ?

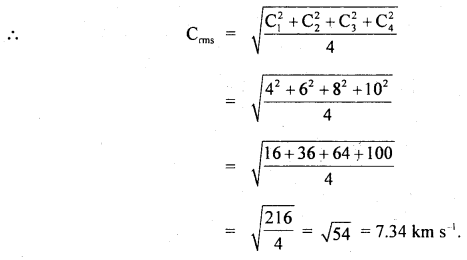
Question 14.
At what temperature, pressure remaining constant, will the RMS velocity of gas on behalf of its value at 0°C?
Answer:
Here, T₁ = 0°C 273 + 0 = 273 K
Let C₁ = rmsvelocityat0°C
Let T₂ be the temperature (= ?) at which rms velocity becomes half
i.e. C₂ = \(\frac{\mathrm{C}_{\mathrm{I}}}{2}\)

Now using the relation, C₂ ∝ T. we get
\(\frac{C_{2}^{2}}{C_{1}^{2}}=\frac{T_{2}}{T_{1}}\)

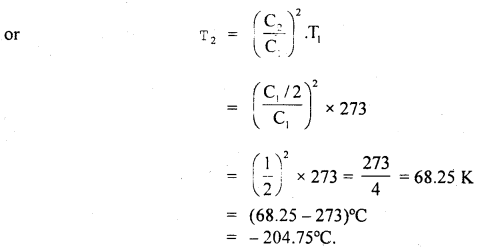
Question 15.
If the density of nitrogen at S.T.P. be 0.00125 g cm³. What is the velocity of its molecules? g = 980 cm
Answer:
Here, P = 1 atm = 76 cm of Hg
= 76 × 13.6 × 980 dyne cm^-2
ρ = density of nitrogen
= 125 × 10^-5 g cm^-3
C_rms = ?

Using the relation,

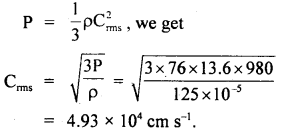
Question 16.
At a certain pressure and 127°C, the average K.E. of a hydrogen molecule is 8 × 10^-27 J. At the same pressure, determine:
(a) ruts velocity of hydrogen molecules at 27°C.
(b) average K.E. of nitrogen molecules at 127°C.
Mass of hydrogen atom = 1.7 × 10^-27 kg.
Answer:
(a) Here, T₁ = 127°C = 127 + 273 = 400 K
E₁ = 8 × 10^-27 J
m = mass of hydrogen molecule
= 2 × 1.7 × 10^-27 kg
= 3.4 × 10^-27 kg

T₂ = 27°C = 27 + 273 = 300 K
E₂ = ?

r.m.s velocity at 27°C, C_rms = ?
Using the relation,
K.E = E ∝ T, we get

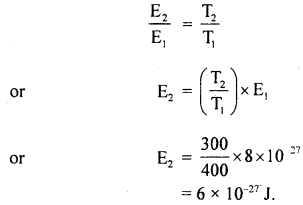
Also, we know that

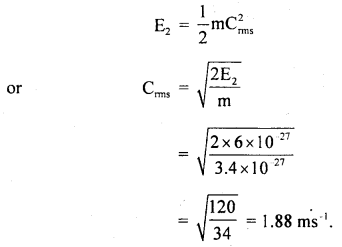
(b) As the average K.E. of a molecule of any gas at the same temperature is the same for all gases, so the average K.E. of nitrogen molecule at 127°C is = 8 × 10^-27 J

Question 17.
Calculate the total random K.E. of one gram of nitrogen at 600 K.
Answer:
Here, T = 600 K
R = 8.31 J/mol/K
M = 28 g = molecular weight of nitrogen

∴ Total random K.E. for 1 g molecule of nitrogen is
E’ = \(\frac{3}{2}\)RT

∴ Total random K.E. for one gram of nitrogen
= \(\frac{3}{2} \frac{\mathrm{R}}{\mathrm{M}}\)T
= \(\frac{3}{2}\) × \(\frac{8.31}{28}\) × 600
= 266.8 J.

Question 18.
Find the temperature at which the RMS velocity of oxygen molecules in the earth’s atmosphere equals the velocity of escape from the earth’s gravitational field.
N = 6.023 × 10²³
R = 6400 km = radius of earth
k = 1.38 × 10^-23 JK^-1
Answer:
Here, N = 6.023 × 10²³
R = 6400 km = 6400 × 10³m
k = 1.38 × 10^-23JK^-1

V_e = escape velocity from earth’s surface
= \(\sqrt{2 \mathrm{gR}_{\mathrm{e}}}\) ….(i)
T = temperature = ?
Let C_rms = rms velocity of oxygen molecules at temp. T0

∴ Using the relation,

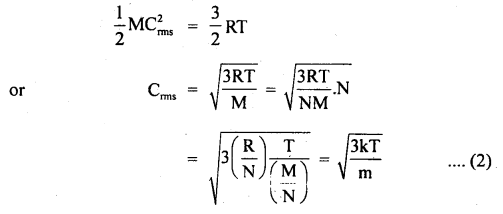
Where m = mass of one molecule = \(\frac{M}{N}\)
k = \(\frac{R}{N}\)

∴ According to the statement,

Question 19.
Calculate the temperature at which r.m.s. the velocity of a gas molecule is the same as that of a molecule of another gas at 27°C. The molecular weights of the two gases are 64 and 32 respectively.
Answer:
Here, T₁ = ? :
T₂ = 27°C = 273 + 27 = 300K
M₁ = 64 .
M₂ = 32
C₁ = C₂

∴ Using the relation,

\(\frac{1}{2}\)MC² = \(\frac{3}{2}\)RT,weget
\(\frac{1}{3}\) M₁C₁²= RT₁ for gas of mass M₁
and \(\frac{1}{3}\)M₂C₂² = RT₂ for gas of mass M₂

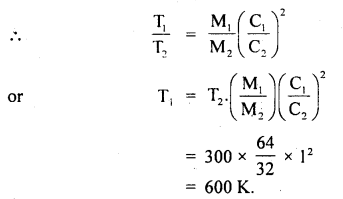
Question 20.
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 125.0 m³ at a temperature of 127°C and 2 atm pressure, k = 1.38 × 10^-23 JK^-1.
Answer:
Here, T = 127°C + 273 = 400 K
k = 1.38 × 10^-23 JK^-1 P = 2 atmosphere
= 2 × 1.01 × 10⁵ Nm^-2
= 2.02 × 10⁵ Nm^-2

V = volume of room = 125 m³
N’ = no. of molecules in the room =?
∴ R = Nk = 6.023 × 10²³ × 1.38 × 10^-23
= 8.31 JK^-1 mol^-1

Let n = no. of moles of the air in the given volume.
∴ Using gas equation,
PV = nRT, we get
n = \(\frac{\mathrm{PV}}{\mathrm{RT}}=\frac{2.02 \times 10^{5} \times 125}{8.31 \times 400}\)
= 7.60 × 103 moles

∴ N’ = Nn = 6.023 × 10²³ × 7.60 × 10³
= 45.77 × 10²⁶.

Question 21.
Calculate the temperature at which the oxygen molecules will have the same r.m.s. velocity as the hydrogen molecules at 150°C. The molecular weight of oxygen is 32 and that of hydrogen is 2.
Answer:
Here, Molecular weight of oxygen, M0 = 32
Molecular weight of hydrogen. MH = 2

Let T₀ = temp. of oxygen = ?
T_H = temp. of hydrogen
= 150°C = 150 + 273 = 423 K
C₀ = C_H

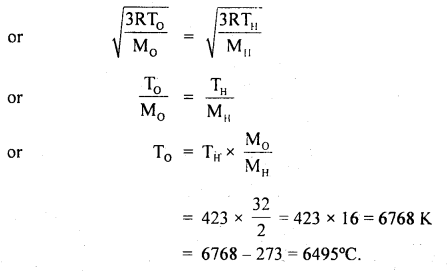
Question 22.
Calculate the r.m.s. the velocity of molecules of gas for which the specific heat at constant pressure is 6.84 cal per g mol per °C. The velocity of sound in the gas being 1300 ms^-1. R = 8.31 × 10⁷ erg per g mol per °C. J = 4.2 × 10⁷ erg cal^-1.
Answer:
Here, C_p = 6.84 cal/g mol/°C
R = 8.31 × 10 erg/g mol/°C
J = 4.2 × 10 erg/cal
v = velocity = 1300 ms^-1
= 1300 × 100 cm s^-1
C_rms =?

Using the relation,


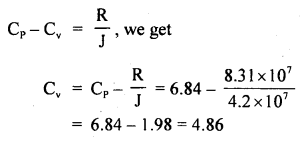
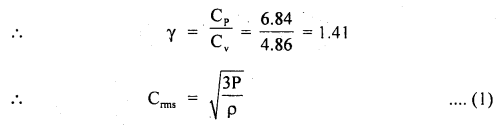
Now using the relation,

Question 23.
Calculate the molecular K.E. of I g of an oxygen molecule at 127°C. Given R = 8.31 JK^-1 mol^-1. The molecular weight of oxygen = 32.
Answer:
Here, M = 32 g
T = 127 + 273 = 400 K

∴ Molecular K.E. of oxygen is given by
\(\frac{1}{2}\) MC² = \(\frac{3}{2}\) RT
Now K.E. of 32 g of O₂ RT = \(\frac{3}{2}\)RT

∴ K.E.of 1 g of O₂ = \(\frac{3}{2} \cdot \frac{\mathrm{RT}}{32}\)
or
E = \(\frac{3}{64}\) × 8.31 × 400 J
= 155.81 J.

Question 24.
Calculate the intermolecular B.E. in eV of water molecules from the following data:
N = 6 × 10²³ per mole
1 eV= 1.6 × 10^-19 J
L = latent heat of vaporisation of water = 22.6 × 10⁵ J/kg.
Answer:
Here, molecular weight of water, M = 2 + 16 = 18g
∴ No. of molecules in 1 kg of water = \(\frac{6 \times 10^{23}}{18}\) × 1000 = \(\frac{10^{26}}{3}\)

L = 22.6 × 10⁵ J kg
∴ B.E .per molecule = 22.6 × 10⁵ J = B.E of \(\frac{6 \times 10^{23}}{18}\) molecule

Thus B.E. per molecule

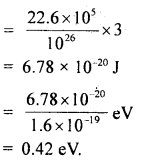
Question 25.
Two perfect gases at absolute temperatures T₁ and T₂ are mixed. There is no loss of energy. Find the temperature of mixture if masses of molecules are m₁ and m₂ and the no. of molecules in the gases are n₁ and n₂ respectively.
Answer:
Let E₁ and E₂ be the K.E. of the two gases,
∴ E₁ = \(\frac{3}{2}\) kT₁ × n₁
and E₂ = \(\frac{3}{2}\) kT₂ × n₂

Let E be the total energy of the two gases before mixing
∴ E = E₁ + E₂ = \(\frac{3}{2}\)K(n₁T₁ + n₂T₂) ….(1)

After mixing the gases, let T be the temperature of the mixture of the two gases
∴ E’ = \(\frac{3}{2}\)kT(n₁ + n₂) …(2)

As there is no loss of energy,

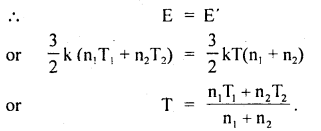
Value-Based Type:

Question 1.
Ram has to attend an interview. He was not well. He took the help of his friend Raman. On the way office, Ram felt giddy, He vomited on his dress. Raman washed his shirt. He made Ram drink enough amount of water. In spite of doing, a foul smell was coming from the shirt. Then Raman purchased a scent bottle from the nearby cosmetics shop and applied to Ram. Ram attended the interview, Performed well. Finally, he was selected.
(a) What values do you find in Raman?
Answer:
He has the presence of mind, serves others in need.

(b) The velocity of air is nearly 500m/s. But the smell of scent spreads very slowly, Why?
Answer:
This is because the air molecules can travel only along a zig-zag path due to frequent collisions. Consequently, the displacement per unit time is considerably small.

Question 2.
One day Shikha got up 7a.ni and saw that the rays of sunlight coming through a narrow hole contains some dust particles which is moving randomly. She kept it her mind and when she reached her school the next day, she first asked her physics teacher the reason behind it. The teacher explained that gas consists of rapidly moving atoms or molecules. The particles may also collide with each other when they come together. She becomes happy to hear the reason. ‘
(i) What values are exhibited by Shikha?
Answer:
Creative, Awareness, willing to know the scientific reasons.

(ii) What is r.m.s velocity?
Answer:
The root mean square speed (r.m.s) of gas molecules is defined as the square root of the mean of squares of the speeds of gas molecules.
i.e Vrms = \(\sqrt{\frac{V_{1}^{2}+V_{2}^{2}+V_{3}^{2}+\ldots \ldots \ldots \ldots \ldots .+V_{n}^{2}}{n}}\)
= \(\sqrt{\frac{3 \mathrm{~K}_{\mathrm{B}} \mathrm{T}}{\mathrm{m}}}\)

(iii) Calculate r.m.s velocity of one gram molecule of hydrogen at S.T.P. [density of hydrogen at S.T.P = 0.09 kg m^-3]
Answer:
According to kinetic theory .of gases:
P = \(\frac{1}{3}\)ρC²
or
C = \(\sqrt{\frac{3 \mathrm{P}}{\rho}}\)

Here, ρ = 0.09 kg m^-3, P = 1.01 × 10⁵ Pa.
∴ C = \(\sqrt{\frac{3 \times 1.01 \times 10^{5}}{0.09}}\)
= 1837.5 ms^-1

Question 3.
During the lecture of physics period, Madan’s teacher Mr Suresh has given a question to the whole class. The question was as under:
“A vessel contains two non-reactive gases: neon (monoatomic) and oxygen (diatomic). The ratio of their partial pressure is 3:2.
Estimate the ratio of
(a) Number of molecules
(b) Mass density
Madan raised his hand to answer the above two questions and gave a satisfactory answer to the question. .
(i) What value is displayed by Madan?
Answer:
He is intelligent, Creative, Sharp minded.

(ii) What explanations would have been given by Madan?
Answer:
(a) Since V and T are common to the two gases
Also, P₁V = μ₁ RT ….(i)
P₂V = μ₂ RT….(ii)

[Using ideal gas equation]
Here, 1 and 2 refer to neon and oxygen respectively
i.e \(\frac{P_{1}}{P_{2}}=\frac{\mu_{1}}{\mu_{2}}\)
⇒ \(\frac{3}{2}=\frac{\mu_{1}}{\mu_{2}}\) {∵ \(\frac{P_{1}}{P_{2}}=\frac{3}{2}\)(given)}

(b) By definition μ1 =\(\frac{\mathrm{N}_{1}}{\mathrm{~N}_{\mathrm{A}}}\) and \(\frac{\mathrm{N}_{2}}{\mathrm{~N}_{\mathrm{A}}}\) where N₁ and N₂ are the number of molecules of 1 and 2 and NA is the Avogadro’s number.
∴ \(\frac{N_{1}}{N_{2}}=\frac{\mu_{1}}{\mu_{2}}=\frac{3}{2}\)

Question 4.
A quiz contest was organized by a public school. They asked rapid-fire questions and decided to give l^st, 2nd and 3rd prizes. The entire class was divided into ten groups and each group has S students.
The questions in the final round were as under:
(i) What is the ideal gas equation?
Answer:
The relationship between Pressure P, Volume V and absolute temperature T of a gas is called its equation of state. The equation of the state of an ideal gas is
PV = μRT

(ii) What would be the effect on the RMS velocity of gas molecules if the temperature of the gas is increased by a factor of 4?
Answer:

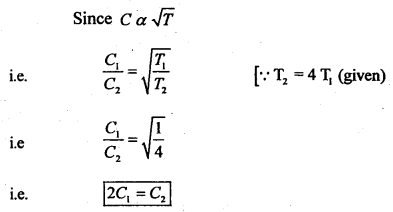
Clearly, ‘C’ will be doubled.

(iii) Which values are being depicted here by the school by ask¬ing the above questions?
Answer:
Values are:
(a) To develop group activity.
(b) To teach in an interesting way.
(c) Award and prizes to motivate them.
(d) To develop leadership quality.