Units and Measurements Class 11 Important Extra Questions Physics Chapter 2

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 2 Units and Measurements Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 2 Important Extra Questions Units and Measurements

Units and Measurements Important Extra Questions Very Short Answer Type

Question 1.
If the size of the atom were enlarged to the tip of the sharp pin, how large would the height of Mount Everest be?
Answer:
10¹⁰ m.

Question 2.
What does the LASER mean?
Answer:
It stands for Light Amplification by Stimulated Emission of Radiation.

Question 3.
If the Universe were shrunk to the size of the Earth, how large would the Earth be on this scale?
Answer:
1o^-11 m (size of an atom.).

Question 4.
A research worker takes 100 careful readings in an experiment. If he repeats the same experiment by taking 400 readings, then by what factor will the probable error be reduced?
Answer:
By a factor of 4.

Question 5.
What is the number of significant figures in 0.06070?
Answer:
4.

Question 6.
Which of the following reading is most accurate?
(a) 7000m,
(b) 7 × 10² m,
(c) 7 × 10³ m
Answer:
(a) i.e. 7000 m.

Question 7.
The density of a cube is calculated by measuring the length of one side and its mass. If the maximum errors in the measurement of mass and length are 3% and 2% respectively, then what is the maximum possible error in the measurement of density?
Answer:
3% + 3 × 2% = 9%.

Question 8.
The mass of a body as measured by two students is given as 1.2 kg and 1.23 kg. Which of the two is more accurate and why?
Answer:
The second measurement is more accurate as it has been made to the second decimal point.

Question 9.
Do the inertial and gravitational masses of ordinary objects differ in magnitude?
Answer:
No.

Question 10.
Are S.I. units Coherent? Why?
Answer:
Yes, because all the derived units in this system can be obtained by multiplying or dividing a certain set of basic units.

Question 11.
Do A.U. And Å represents the same magnitudes of distance?
Answer:
No, 1 A.U. = 1.496 × 10¹¹ m and 1 Å = 10¹⁰ m.

Question 12.
What does SONAR stand for?
Answer:
It stands for Sound Navigation and Ranging.

Question 13.
What is the atomic mass unit (a.m.u.)?
Answer:
It is defined as \(\frac{1}{12}\)th of the mass of one 6C12 atom
i.e. 1 a.m.u. = \(\frac{1}{12} \times \frac{12}{6.023 \times 10^{23}}\) = 1.66 × 10^-27 kg

Question 14.
Which is the most accurate clock?
Answer:
Cesium atomic clock.

Question 15.
Write the S.I. units of the following physical quantities:
(a) Luminous intensity
Answer:
Candela (cd)

(b) Temperature
Answer:
Kelvin (K)

(c) Electric current
Answer:
Ampere (A)

(d) Amount of substance
Answer:
Mole (mol)

(e) Plane angle
Answer:
Radian (rd)

(f) Solid angle
Answer:
Steradian (sr)

(g) Pressure.
Answer:
Nm-2 = pascal (pa).

Question 16.
What is the difference between mN, Nm, and nm?
Answer:

• mN means.milli-newton, 1 mN = 10^-3N.
• Nm means newton-meter, 1 Nm = 1 J
• nm means namometer, 1 nm = 10^-9 m.

Question 17.
If x = a + bt + ct² where x is in meter and t in seconds, what is the unit of c?
Answer:
The unit on the left-hand side is a meter so the units of ct² should also be a meter. Since t² has units of s², so the unit of c is ms^-2

Question 18.
Will the dimensions of a physical quantity be the same, whatever be the units in which it is measured? Why?
Answer:
Yes, the dimensions don’t depend on the system of units chosen.

Question 19.
Write the dimensions of:
(i) gravitational constant
Answer:
[M^-1 L³ T²]

(ii) Plank’s constant
Answer:
[M L² T^-1]

(iii) torque
Answer:
[M L² T²]

(iv) surface tension
Answer:
[M L⁰ T^-2]

(v) angular momentum.
Answer:
[M L² T^-1]

Question 20.
Name at least two physical quantities each having dimensions:
(a) [M L^-1 T^-2]
Answer:
Pressure and stress,

(b) [M L² T^-1]
Answer:
Plank’s constant and angular momentum.

Question 21.
State the principle of homogeneity of dimensions?
Answer:
It states that the dimensions of each term on both sides of an equation are the same.

Question 22.
Which are the main types of errors in a physical measurement?
Answer:
Main errors are systematic error, random error, gross error, relative error, and percentage error.

Question 23.
Which one is large, the number of microseconds in a second or the number of seconds in a year?
The number of seconds in a year = 10⁷s and the number of microseconds in a second = 10⁶μs. So the number of seconds in a year is larger than microseconds in a second.

Question 24.
Do significant figures change if the physical quantity is measured in different systems of units?
Answer:
No, significant figures don’t depend on the system of units. e.s. 250 g = 2.50 × 10^-1 kg.
Both have 3 significant figures.

Question 25.
Suggest a distance corresponding to each of the following order of length:
(a) 10^-4 m
Answer:
Size of the atomic nucleus

(b) 10^-9 m
Answer:
Size of the oil molecule

(c) 10⁴ m
Answer:
Height of Mount Everest

(d) 10⁷ m
Answer:
Radius of Earth

(e) 10⁹ m.
Answer:
The radius of Sun.

Question 26.
What do you understand by the following?
(a) Century
Answer:
It is the largést unit of time, 1 century = 100 years.

(b) Shake
Answer:
It is the smallest unit of time, 1 shake = 10^-8s.

(c) Lunar month
Answer:
It is the time taken by the moon to complete one revolution around the Earth, 1 lunar month = 27.3 days.

(d) Leap year
Answer:
A year that is divisible by four and in which the month of February is of 29 days is called a leap year.

(e) Tropical year.
Answer:
The year in which the total solar eclipse takes place is called a tropical year.

Question 27.
What is the role of power (index) of a measurable in the formula used for calculation of a quantity in regard to the error in the quantity as determined in the given experiment?
Answer:
The error in the quantity becomes power times the error,
i.e. if x = p^a q^b. Then
\(\frac{\Delta x}{x}=a \frac{\Delta p}{p}+b \frac{\Delta q}{q}\)

Question 28.
How will you find the size of a liquid molecule?
Answer:
Using the formula, t = \(\frac{\mathrm{nV}}{500 \mathrm{~A}}\) we can find the size of the liquid molecule.
where V = volume of liquid (say oleic acid),
n = no. of drops in the solution of \(\frac{1}{500}\) concentration
A = area of the film of oleic acid left
t = thickness of the film.

Question 29.
What do you mean by the term measurement?
Answer:
Measurement means the comparison of a physical quantity with its unit to find out how many times the unit is contained in the given physical quantity.

Question 30.
Sort out the incorrect representation of units and write them
(i) m/sec
Answer:
ms^-1

(ii) Newton
Answer:
newton

(iii) kelvin
Answer:
kelvin

(iv) m.m.
Answer:
mm

(v) Jk^-1
Answer:
JK^-1

(vi) kg/m³
Answer:
kgm^-3

(vii) wH
Answer:
Wh

(viii) gms^-2
Answer:
gs2

(ix) length = 5M
Answer:
length = 5 m

(x) B = 4g (B = magnetic field intensity).
Answer:
B = 4G

Question 31.
Define light year.
Answer:
It is defined as the distance traveled by light in one year.
1 L.Y. (ly) = 3 × 10⁸ ms^-1 × 365 × 24 × 60 × 60s ≈ 9.46 × 10¹⁵ m.

Question 32.
Define Astronomical distance.
Answer:
It is defined as the distance between the Earth and Sun.
1 A.U. = 1.496 × 10¹¹ m~ 1.5 × 10¹¹ m.

Question 33.
What is the limit of
(i) accuracy
Answer:
The least count of the measuring instrument is the limit of accuracy with which a physical quantity can be measured.

(ii) error?
Answer:
The error in measurement is taken equal to half the least count.

Question 34.
What do you mean by ‘Order of magnitude’?
Answer:
Order of magnitude is defined as the approximation to the nearest power of 10 used to express the magnitude of a physical quantity under consideration, e.g.

1. The order of magnitude of the time interval of 1.2 × 10^-6 s is -6.
2. The order of magnitude of the distance of 4.5 × 10⁶ is +6.

Question 35.
Find the order of magnitude of a light-year.
Answer:
I light year = 9.46 × 10¹⁵ m ≈ 10¹⁶m
∴ The order of magnitude of light-year is +16.

Question 36.
Derive the dimensional formula of:
(a) Angular velocity
Answer:
Angular velocity = \(\frac{\text { Angle }}{\text { Time }}=\frac{1}{\mathrm{~T}}\) = [M⁰ L⁰ T^-1]

(b) Angular momentum
Answer:
Angular momentum = momentot inertia × Angular velocity
= mass x (radius of rotalion)² (Time)^-1
= [M L² T^-1].

Question 37.
Derive the dimensional formula of:
(a) Impulse
Answer:
Impulse = Force x Time
= [M L T^-2][T]
= [M L² T^-1].

(b) Surface energy
Answer:
Surfäce energy = \(\frac{\text { Energy }}{\text { Surface area }}\)
= \(\frac{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]}{\left[\mathrm{L}^{2}\right]}\)
= [M L⁰ T^-2].

Question 38.
Derive the dimensional formula of
(a) Specific gravity
Answer:
Specific gravity = \(\frac{\text { Density of substance }}{\text { Density of water at } 4^{\circ} \mathrm{C}}\)
= \(\frac{\left[\mathrm{ML}^{3} \mathrm{~T}^{0}\right]}{\left[\mathrm{ML}^{-3} \mathrm{~T}^{0}\right]}\)
= [M⁰ L⁰ T⁰]

(b) Coefficient of viscosity .
Answer:
Coefficient of viscosity = \(\frac{\text { Force } \times \text { Distance }}{\text { Area } \times \text { velocity }}\)
= \(\frac{\left[\mathrm{MLT}^{-2}\right][\mathrm{L}]}{\left[\mathrm{L}^{2}\right]\left[\mathrm{LT}^{-1}\right]}\)
= [M L^-1 T^-1]

Question 39.
Derive the dimensional formula of:
(a) Universal gas constant
Answer:
Universal gas constant = \(\frac{\text { Pressure } \times \text { Volume }}{\text { Temperature }}\)
= \(\frac{\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]\left[\mathrm{L}^{3}\right]}{[\mathrm{K}]}\)
= [M L²  T² K^-1]

(b) Specific heat.
Answer:
Specific heat = \(\frac{\text { Heat }}{\text { Mass } \times \text { Temperature }}\)
= \(\frac{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]}{[\mathrm{MK}]}\)
= [M⁰ L² T^-2 K^-1].

Question 40.
Derive the dimensional formula of:
(a) Coefficient of elasticity
Answer:
Coefficient of elasticity = \(\frac{\text { Stress }}{\text { Strain }}\)
= \(\frac{\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]}{\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right]}\)
= [M L^-1 T^-2]

(B) Boltzmann’s constant
Answer:
Boltzmann’s constant = \(\frac{\text { Energy }}{\text { Temperature }}\)
= \(\frac{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]}{[\mathrm{K}]}\)
= [M L² T^-2 K^-1]

Question 41.
Define dimensions of a physical quantity.
Answer:
They are defined as the powers to which the fundamental units of mass, length, and time have to be raised to obtain its units, e.g. derived unit of area is [M⁰ L² T⁰]. Thus its dimensions are 1 zero in mass, 2 in length, and zero in time.

Question 42.
Define the dimensional formula of a physical quantity.
Answer:
It is defined as an expression that shows which of the fundamental units and with what powers appear into the derived unit of a physical quantity.
e.g. dimensional formula of force is [M¹ L¹ T²].

Question 43.
Define dimensional equation of a physical quantity.
Answer:
It is defined as the equation obtained by equating the symbol of a physical quantity with its dimensional formula, e.g. [F] = [M L T^-2] is the dimensional equation of force.

Question 44.
Define one kilogram.
Answer:
It is the mass of platinum-iridium cylinder (90% Pt + 10% Ir) having its diameter equal to its height (both equal to 3.9 cm) kept in the International Bureau of Weights and Measures of Sevres near Paris.

Question 45.
Define one second.
Answer:
It is defined as the time interval occupied by 9, 192, 631, 770 vibrations corresponding to the transition between two hyperfine levels of cesium -133 (Cs¹³³) atom in the ground state.

Question 46.
Define one ampere.
Answer:
It is defined as that constant current which when flowing through two parallel, straight conductors of the infinite length of negligible cross-section held one meter apart in a vacuum produces a force of 2 × 10^-7 N/m between them.

Question 47.
Define Kelvin.
Answer:
It is defined as \(\frac{1}{273.16}\) fraction of the thermodynamic temperature at the triple point of water.

Question 48.
Define radian.
Answer:
It is defined as the angle made at the center of a circle by an arc of length equal to the radius of the circle.

Question 49.
Define steradian.
Answer:
It is defined as the solid angle made at the center of a sphere by an area cut from its surface whose area is equal to the square of the radius of the sphere.

Question 50.
Define one mole.
Answer:
It is defined as the amount of substance that contains the same number of elementary units {i.e. atoms) as there are atoms in 0.012 kg of carbon-12.

Question 51.
Define standard meter.
Answer:
It is defined to be equal to exactly 1650763.73 wavelengths of orange-red light emitted in vacuum by krypton-86 atom i.e. kr⁸⁶.
i. e. 1 metre = 16,50,763.73 wavelengths.
Or
It is also defined as the distance traveled by light in \(\frac{1}{299792458}\) second.

Here 299792458 ms^-1 is the exact value of the velocity of light.

For all practical purposes, c = 2.9 × 10⁸ ms^-1 = 3.0 × 10⁸ ms^-1.

Units and Measurements Important Extra Questions Short Answer Type

Question 1.
If the size of a nucleus is scaled up to the tip of a sharp pin, what roughly is the size of an atom?
Answer:
The size of a nucleus is in the range of 10^-15 m to 10^-14 m. The tip of a sharp pain may be taken to be in the range of 1o^-5 m to 10^-4 m. Thus we are scaling up the size of the nucleus by a factor of 10^-5/10^-15 = 10¹⁰. An atom roughly of size 10^-10 m will be scaled up to a rough size of 10^-10 × 10¹⁰ = 1 m. Thusanucleus in an átom is as small in size as the tip of a sharp pin placed at the center of a sphere of radius about a meter.

Question 2.
(a) What do you mean by physical quantity?
Answer:
It is defined as a quantity that can be measured, e.g. mass, length, time, etc.

(b) What do you understand by:
(i) Fundamental physical quantities?
Answer:
They are defined as those quantities which cannot be expressed in terms of other quantities and are independent of each other, e.g. mass, length, time.

(ii) Derived physical quantities?
Answer:
They are defined as the quantities which can be expressed in terms of fundamental quantities, e.g. velocity, acceleration, density, pressure, etc.

Question 3.
(a) Define the unit of a physical quantity.
Answer:
It is defined as the reference standard used to measure a physical quantity.

(b) Define:
(i) Fundamental units.
Answer:
They are defined as the units of fundamental quantities. They are independent of each other and are expressed by writing the letter of the fundamental quantity in a parenthesis.
e.g. Fundamental units of mass, length and time are [M], [L], [T] respectively.

(ii) Derived units.
Answer:
They are defined as those units which can be derived from fundamental units. They are expressed by writing the symbol of a derived quantity in a parenthesis.
e.g. D.U. of velocity = [u]
acceleration = [a]
pressure = [P]
work = [W] and so on.

Question 4.
Define one Candela.
Answer:
It is defined as the luminous intensity in a perpendicular direction of a surface of \(\frac{1}{600,000}\) square meter area of a black body at a temperature of freezing platinum (1773°C) under a pressure of 101,325 N/m².

It is the S.I. unit of luminous intensity.

Question 5.
What is the advantage of choosing wavelength of light radiation as standard of length?
Answer:

1. It can be easily made available in any standard laboratory as Krypton is available everywhere.
2. It is well defined and does not change with temperature, time, place or pressure, etc.
3. It is invariable.
4. It increases the accuracy of the measurement of length (1 part in 10⁹).

Question 6.
Which type of phenomenon can be used as a measure of time? Give two examples of it.
Answer:
Any phenomenon that repeats itself regularly at equal intervals of time can be used to measure time.

The examples are:

1. Rotation of earth – the time interval for one complete rotation is called a day.
2. Oscillations of a pendulum.

Question 7.
Find the number of times the heart of a human being beats in 10 years. Assume that the heartbeats once in 0.8s.
Answer:
In 0.8 s, the human heart makes one beat.

∴ In 1 s, the human heart makes = \(\frac{1}{0.8}=\frac{10}{8}\) beats.

∴ In 10 years, the human heart makes
= \(\frac{10}{8}\) × 365 × 24 × 60 × 60 beats.
= 3.942 × 10⁸ beats.

Question 8.
Why it is not possible to establish a physical relation involving more than three variables using the method of dimensions?
Answer:
The dimensional analysis fails to derive a relation involving more than three unknown variables. The reason is that there will be more than three unknown factors in that case whose values cannot be determined from the three relations which we get by comparing the powers of M, L, and T.

Question 9.
What is the difference between accurate and precise measurement?
Answer:
A given measurement is said to be accurate in relation to other similar measurements if the error involved in it is least.

A given measurement is said to be precise in relation to other similar measurements if it is taken with an instrument with the minimum least count.

Question 10.
Pick up the most accurate and most precise measurement out of (a) 50.0 m, (b) s.oe m, (e) 5.00 cm, (f) 5.00 mm.
Answer:
The following table gives the relative error in count of the given measurement:

l	Δl	Δl/l
50.00 m	0.01 m	0.01/50 = 0.2 × 10-3
5.00 m	0.01 m	0.01/5 = 0.2 × 10-2
5.00 cm	0.01 cm	0.01/5 = 0.2 × 10-2
5.00 mm	0.01 mm	0.01/5 = 0.2 × 10-2

Clearly, the first measurement is most accurate because the relative error in it is minimum. The fourth measurement is most precise because it is taken with an instrument having the minimum least count among the v given measurements.

Question 11.
Define one parsec.
Answer:
It is defined as the distance at which an arc of length equal to y one astronomical unit subtends an angle of one second at a point.


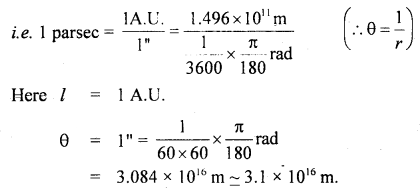
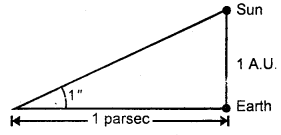
Note: 1 L.Y. = 6.3 × 10⁴ A.U.
1 parsec = 3.26 L.Y.

Question 12.
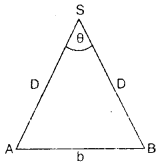
Define annual parallax.
Answer:
It is defined as the angle (θ) subtended by the basis at the object (0). It is also called the parallactic angle.

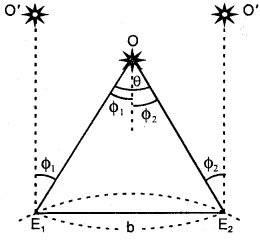
∴ Parallactic angle = \(\frac{\text { Length of arc }}{\text { Radius }}\)
Or
θ = \(\frac{b}{s}\)

∴ s = \(\frac{b}{θ}\)

The parallax method is used to measure the distance of stars.
Here, b = basis = E₁E₂ distance where E₁ and E₂ are the two observation points on earth. θ = angle made by the star at point O. To find θ, let us observe the star 0’ simultaneously and let Φ₁ and Φ₂ be the angles made at E₁ and E₂.
∴ θ = Φ₁ + Φ₂
∴ s = \(\frac{b}{\phi_{1}+\phi_{2}}\)

Question 13.
Give Avogadro’s method to measure distances of the order of 10^-10 m.
Answer:
It is the indirect method of measuring the distances of the order of 10-10 m which is the size of an atom i.e. small distances. An atom is a tiny sphere. When such atoms lie packed in any substance; empty spaces are left in between. According to Avogadro’s hypothesis, the volume of all atoms in one gram of substance is \(\frac{2}{3}\) of the volume occupied by one gram of the substance.

i.e. V’ = \(\frac{2}{3}\)V ….(i)
Where V = actual volume of one gram mass.
V’ = volume occupied by atoms in I gram mass.
ρ = density of the substance.
∴ V = \(\frac{1}{ρ}\) …(ii)

Let m = atomic weight of the substance.
N = Avogadro’s number

∴Number of atoms in I gram of the substance = \(\frac{N}{M}\)
If r be the radius of each atom, then
V’ = no. of atoms in I gram x volume of each atom
Or
V’ = \(\frac{N}{M}\) x \(\frac{4}{3}\) 4πr3 …. (iii)

∴ From (i), (ii), and (iii), we get

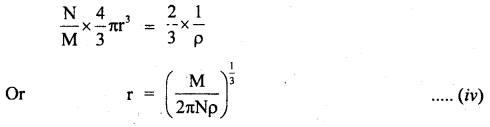
Thus, r the radius of an atom can be calculated from equation (iv).

Question 14.
What arè the characteristics of a standard unit?
Answer:
The characteristics of a standard unit are as follows:

1. It should be well defined.
2. It should be of the proper size.
3. It should be easily accessible.
4. It should be reproducible in all places.
5. It should not change with time, place, and physical conditions such as pressure, tèmperature, etc.
6. It should be widely accepted.

Question 15.
What are the advantages of the S.I. system?
Answer:
Following are the main advantages of the S.I. system over other systems of units i.e. (C.G.S, FPS, and MKS).
1. It is a coherent system of units i.e. a system based on a certain set of fundamental units from which all derived units are obtained by multiplication or division without introducing numerical factors i.e. units of a given quantity are related to one another by the power of 10. So the conversions are easy.

2. S.I. is a rational system of units as it assigns only one unit to a particular physical quantity e.g. Joule is the S.I. unit for all types of energies while MKS units of mechanical energy, heat energy, and electrical energy are Joule, calorie, and watt-hour respectively.

3. It is an absolute system of units: There are no gravitational units on the system. The use of factor ‘g’ is thus eliminated.

4. It is a metric system i.e. the multiples and submultiples of units are expressed as powers of 10.

Question 16.
Point out the measurable likely to create the maximum error in the following experimental measurement.
Young’s modulus ‘Y’ of the material of the beam is calculated using the relation Y = mgl³/4bd³δ
When w = mg, δ = depression, I, b, d = length, breadth, thickness.
Answer:

Thus clearly m, l, b, d and 8 introduce the maximum error in the measurement of Y.

Question 17.
Classify the physical quantities on basis of their dimensional formula.
Answer:
They are divided into the following four categories:
1. Dimensional variables: They are defined as the physical quantities which possess dimensions and have variable values e.g. Area, velocity, force, etc.

2. Non-dimensional variables: They are defined as the physical quantities which have no dimensions but have variable values, e.g. Angle, specific gravity, strain, sin0, cos0 (i.e. trigonometric functions).

3. Dimensional constants: They are defined as the physical quantities which have both dimensions and constant values, e.g. Plank’s constant, speed of light in vacuum, gravitational constant.

4. Dimensionless constants: They are defined as the physical quantities which do not have dimensions but have constant values, e.g. n, e, pure numbers 1, 2, 3, …… etc.

Question 18.
What are the limitations of dimensional analysis?
Answer:
Following are the limitations of dimensional analysis:

1. Dimensionless constants involved in the physical relationship can not be determined.
2. It fails to derive the relations involving plus or minus signs like s = ut + \(\frac{1}{2}\)at²,
   v = u + at,
   v² — u² = 2as etc.
3. It fails to derive a relation involving more than three physical quantities.
4. This method does not help to derive the relations containing exponential and trigonometrical functions.
5. This method gives no information on whether a quantity is a scalar or vector.
6. It does not tell about the physical correctness of a relation.

Question 19.
Define significant figures. State the rules for determining the number of significant figures in a given measurement.
Answer:
They are defined as the number of digits up to which we are sure about their accuracy. In other words, they are defined as those digits that are known correctly in an experimental observation plus one more digit that is uncertain.

Following are the rules for determining significant figures:

1. All non-zero digits are significant.
2. All zeros occurring between non-zero digits are significant.
3. All zeros to the right of the last non-zero digit are not significant.
4. All zeros to the right of a decimal point and to the left of a non¬zero digit are not significant, e.g. 0.000879 has (3) significant figures.
5. All zeros to the right of a decimal point and to the right of a non-zero digit are significant, e.g. 0.2370 contains (4) sig-fig.
6. All zeros to the right of a non-zero digit and to the left of an expressed decimal are significant, e.g. 21900. has (5) sig-fig.

Question 20.
Mankind has existed for about 10⁶ years whereas the s. the universe is about 1010 years old. If the age of the universe is taken to be one day, how many seconds has mankind existed?
Answer:
Since

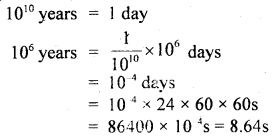
Mankind has existed for 8.64s on the new chosen scale.

Question 21.
State and explain the rule for finding the maximum possible error in a result.
Answer:
The maximum possible error is found in different ways in different types of results as follows:
(a) When the result involves the sum of two quantities,
i. e. if x = p + q
then, maximum possible error = maximum absolute error in first quality + maximum absolute error in the second quality. i.e. Δx = Δp + Δq

(b) When the result involves the difference of the quantities
i.e. if x = p – q
then, maximum possible error in x = maximum absolute error in p + maximum possible error in q
i.e. Δx = Δp + Δq

(c) When the result involves the multiplication of two quantities i.e. x = pq; then maximum relative error in x is given by
\(\frac{\Delta x}{x}=\frac{\Delta p}{p}+\frac{\Delta q}{q}\)

(d) When the result involves the quotient of tw«j observed quantities i.e. when x = p/q, then Maximum relative error in x is given by
\(\frac{\Delta x}{x}=\frac{\Delta p}{p}+\frac{\Delta q}{q}\)

(e) When the result involves some power oFa physical quantity, i.e. when x = pa qb, then maximum absolute e> u r in x is given by
\(\frac{\Delta x}{x}=a \frac{\Delta p}{p}+b \frac{\Delta q}{q}\)

i.e. maximum possible relative error in x = power × relative . error in p + power × relative error in q.

Thus the error is always additive in nature and maximum, permissible error is equal to the sum of maximum possible error in the i. individual quantities of that quantity.

Question 22.
How do you represent very large and very small physical y quantities? Write the prefixes, multiple, submultiple, and their symbols in a tabular form.
Answer:
The very long and very small quantities are written in powers of 10. The prefixes are tabled below:

S.No. Power of 10	Prefix	Symbol
1. 1012	Tera (Trillion)	T
2. 109	Giga (billion)	G
3. 106	mega(million)	M
4. 103	kilo	K
5. 102	Hecta	h
6. 101	Deca	da
7. 10-1	Deci	d
8. 10-2	Centi	c
9. 10-3	mull	m
10. 10-6	micro	u
11. 10-9	nano	n
12. 10-12	pico	p
13. 10-15	femto	f
14. 10-18	Atto	a

Question 23.
Explain the importance of reference frames in measurements.
Answer:
(a) All measurements are made with reference to a point or portion i.e., a frame of reference.
(b) The number of time units contained in a physical quantity gets changed with a change in the reference frame.
(c) The same physical quantity may have different values in different reference frames.

Question 24.
Briefly describe the various techniques to measure time.
Answer:
The various techniques to measure time are:
(a) The synchronous motor run on a.c. of frequency 50 hertz is used to measure time as its rotation provides a time scale.

(b) Electronic oscillations: The semiconductor oscillators produce high-frequency oscillations i.e. of a very small time period. These oscillations thus can be used to measure the small time intervals.

(c) Quartz-crystal clocks: These clocks work on the piezoelectric effect. The oscillations so produced can be used to measure time intervals.

(d) Atomic clock: These are usually Cs-133 atom clocks whose electrons make a definite number of repeated jumps between two energy levels. These are very precise and are used to define second, so time can be measured.

(e) Decay of elementary particles: The study of decay can provide a scale for the measurement of very small intervals of time as unstable elementary particles decay between 10^-16 to 10^-24 seconds.

(f) Radioactive dating: Very long intervals of time can be measured by comparing them with the techniques of radioactive dating. The half-life period of decay of carbon is a standard time frame to determine the age of fossils etc.

Question 25.
Explain the rules for finding significant figures in the sum, difference, product, and quotients of true numbers.
Answer:
The rules for counting significant figures in algebraic operations are given below:
1. Addition and Subtraction: The sum or the difference of two numbers has significant figures only in those places where these are in the least precise amongst the given number. For example, if we subtract 45.7 from 46.9267 the result is 1.2267. But it should be written only 1.2 because the least precise of the two numbers is 45.7 and there is only one digit after the decimal.

Similarly in the sum of numbers 4205, 112.39, 77.93, and 213.2532, the correct result is 824.0 to the significant figures. So, in addition, or subtraction the same number of the decimal. places are retained in the result as are present in the number with the minimum amount of decimal places.

2. Multiplication and Division: The product or quotient of two numbers does not have more significant figures than are present in the least precise of the given numbers. e.g. in the product of two quantities 0.025 with 40, we get 1.000 but the answer is to be written as 1.0 because there are two significant figures in 40 the least of the two numbers. Similarly in a quotient when we divide 16.775 by 2.5, we get 6.71. The result of the significant figure will be 6.7.

Question 26.
Is it possible for an equation to be dimensionally correct still to be wrong? If so indicate the number of ways in which this might happen.
Answer:
It is possible that an equation may be dimensionally correct but physically it is wrong. For example the displacement of a particle moving with velocity u and acceleration ‘a’ after time t is given by
s = ut + 1/2at²

However, s = 1/2at² is dimensionally correct, as [L] = [LT²][T²]² shows dimensions on LHS = dimensions on RHS. Therefore, in certain circumstances, an equation may be dimensionally correct but actually, it is not physically correct. This happens especially in equations involving the sum and difference of two or more terms and in functions involving trigonometric functions. For example, the displacement y maybe y = a where a is the amplitude. This is dimensionally correct but does not give the full picture of the physical phenomenon.

The correct equation is

y = a sin wt or y = a sin \(\frac{2 \pi}{\lambda}\) (vt + x) etc.

Question 27.
Show that bigger is the unit smaller is the numerical value of physical quantity and vice-versa.
Answer:
In any system of unit, the following relations hold good
n₁u₁ = n₂u₂

Where n₁ and n₂ are the numerical values, u₁ and u₂ represent the unit of a physical quantity. This relation is based on the simple thing that the magnitude of a physical quantity remains the same in different systems of units.
Thus nu = constant or n ∝ \(\frac{1}{u}\)

If larger the n smaller will be the unit (u) and smaller the numerical value (n) Larger will be u. E.g. if the length of a rod l be 1 m in the S.I. system. Then it is 100 cm in the C.G.S. system i.e.

l = 1 m = 100 cm. Here clearly 1 < 100 and m > cm. Hence proved.

Question 28.
The difference in the order of magnitude of the longest and shortest distances and most massive and least massive objects are quite different. Write the same and compare them.
Answer:
The size of the nucleus is of the order 10^-15 m and the intergalactic distance is of the order of 10²² m. So, the ratio between the longest and the shortest distance is:
\(\frac{10^{22} \mathrm{~m}}{10^{-15} \mathrm{~m}}\) = 10³⁷

The smallest mass is the mass of an electron of the order of 10^-30 kg and the longest mass is the mass of the galaxy of the order of 10⁴² kg. So, the ratio of maximum to minimum mass is
\(\frac{10^{42} \mathrm{~kg}}{10^{-30} \mathrm{~kg}}\) = 10⁷²

Now the ratio between the mass ratio and distance ratio is
\(\frac{10^{72}}{10^{37}}\) = 10³⁵

The ratio betwe< n minimum mass and minimum distance is
\(\frac{10^{-30} \mathrm{~kg}}{10^{-15} \mathrm{~m}}\) = 10^-15

The ratio between maximum mass and minimum distance is
\(\frac{10^{42} \mathrm{~kg}}{10^{22} \mathrm{~m}}\) = 10²⁰

Question 29.
Define the terms
(i) mean absolute error
Answer:
The arithmetic means of all the absolute errors is known as mean absolute error.

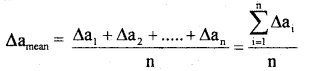
(ii) relative error and
Answer:
The relative error is the ratio of mean absolute error to the mean or true value of the quantity measured.
Relative error = \(\frac{\Delta \mathrm{a}_{\text {mean }}}{\mathrm{a}_{\text {mean }}}\)

(iii) percentage error.
Answer:
Percentage error is the relative error expressed in percent
Percentage error = \(\frac{\Delta \mathrm{a}_{\text {mean }}}{\mathrm{a}_{\text {mean }}}\) × 100

Question 30.
State the rules applied in rounding off measurements.
Answer:
While rounding off measurements, the following rules are applied:
1. If the digit to be dropped is smaller than 5, then the preceding digit should be left unchanged.
e.g. 7.93 is rounded off to 7.9.

2. If the digit to be dropped is greater than 5, then the preceding digit should be raised by 1.
e.g. 17.26 is rounded off to 17.3.

3. If the digit to be dropped in 5 followed by digits other than zero, then the preceding digit should be raised by 1.
e.g. 7.351 on being rounded off to first decimal becomes 7.4.

4. If the digit to be dropped in 5 or 5 followed by zeros, then the preceding digits are not changed if it is even.
e.g. (a) 3.45 on being rounded off becomes 3.4.
(b) 3.450 on being rounded off becomes 3.4.

5. If the digit to be dropped in 5 or 5 followed by zeros, then the preceding digit is raised by one if it is odd.
e.g. (a) 3.35 on being rounded off becomes 3.4.
(b) 3.50 on being rounded off becomes 3.4.

Note: Rules (iv) are based on the convention that the number is to be rounded off to the nearest even number.

Units and Measurements Important Extra Questions Long Answer Type

Question 1.
State the rules for writing the units of physical quantities in the S.I. system.
Answer:
While writing the units of physical quantities following rules are followed with S.L units:
(1) The S.l. units are written in the form of symbols after the number i.e., number of time, the unit is contained in the physical quantity so that physical quantity = nu

With symbols, certain rules are laid down:

• Units in symbols are never written in plural i.e., meters is only m and not ms, years is y.
• The units based on the name of the scientists are written beginning with small letters and with capital letters in symbolic form viz, weber (Wb), newton (N), etc.
• No full stop is used at the end of the symbol.
• Symbols of units not based on the name of scientists are written as small letters viz. kilogram (kg), second (s), etc.

(2) Bigger and smaller number of units are represented with symbols corresponding to the power of 10 viz. 10⁶ is mega (M), 10¹² is Tera (T), 10^-3 is milli (m), 10^-9 is nano (n), etc.

(3) All units are written in numerator viz. kg/m³ is kg m, Nm²c².

(4) The units are written within parenthesis in graphs below the corresponding taxes viz. (ms^-1) and (s) in the velocity-time graph.

(5) Units of a similar physical quantity can be added or subtracted.

Question 2.
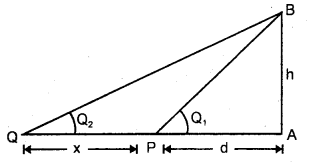
Explain the Triangular method.
Answer:
It is used to measure the distance of an accessible or inaccessible hill or a tower by measuring the angle which the object makes at point P (say)

Let x = distancy of point P from the foot of tower = PA .
∴ h = x tan θ

It is also used to measure the distance of an inaccessible object eg. a tree on the other bank of a river.

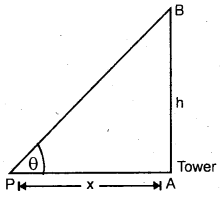
Let h = height of the inaccessible object.
Let θ₁, θ₂ = be the angle made at P and Q by the object.
Let PA = d, PQ = x.

∴ In ΔPAB and ΔQAB,

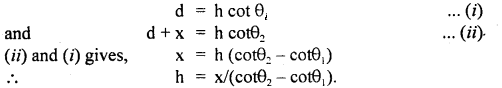
Question 3.
What are the uses of dimensional analysis? Explain each of them.
Answer:
Dimensional analysis is used for:
(a) checking the dimensional correctness of the given physical equation or relation.
(b) converting one system of units to another system.
(c) deriving the relationship between various physical quantities.

(a) checking of the dimensional correctness of a physical relationship is done by using the principle of homogeneity of dimensions. If the dimensions of M, L, T of each term on R.H.S. are equal to the dimensions of M, L, T of each term on L.H.S., then the given- physical relation is dimensionally correct, otherwise wrong.

(b) conversion: It is based on the fact that the magnitude of a physical quantity remains the same whatever may be the system of units, i.e. n₁u₁ = n₂u₂.

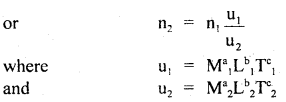
are the units of M, L, T in the first and second system of units of a physical quantity having dimensions of M, L, T, and a, b, c respectively.

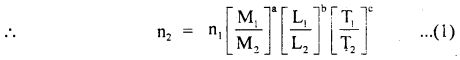
Thus if fundamental units of both systems, dimensions of the quantity, and its numerical value n₁ in one system, are known then we can easily calculate n₂ in another system.

(c) Derivation of a relationship between various physical quantities is based on the principle of homogeneity of dimensions.

Following are the steps used:

1. We must Know the physical quantities (say p, q, r) upon which a physical quantity say x depends.
2. We must know the dimensions of p, q, r say a, b, c respectively.
3. 
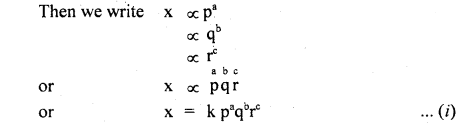
4. Now, write the dimensions of each physical quantity on both sides of the equation
5. and compare the powers of M, L, T to find a, b, c. Putting values of a, b, c in the equation
6. we get the required relation.

Numerical Problems:

Question 1.
The average distance from Earth to the Sun is 1.49 × 10¹¹ m. Find out the value of 1 percent in m.
Answer:
According to the definition of parsec,

Question 2.
The parallax of a heavenly body measured from two points: diametrically opposite on the Earth’s equator is 60 seconds. If the radius of the Earth is 6.4 × 10⁶ m, determine the distance of the heavenly body from the center of Earth. Convert this distance in AU.
Answer:
Here

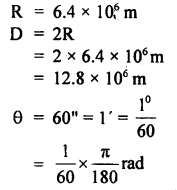
∴ The distance of the heavenly body from Earth is given by

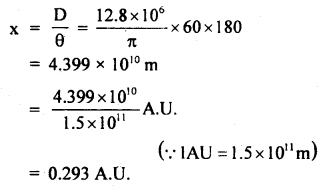
Question 3.
Find the height of a rock mountain if on moving 100 m towards the rock in the horizontal direction through the base of
the rock, the angle of elevation of itš top increases from 300 to 45°.
Answer:
Here d = 100 m, θ₁ = 30°, θ₂ = 45°, h =?

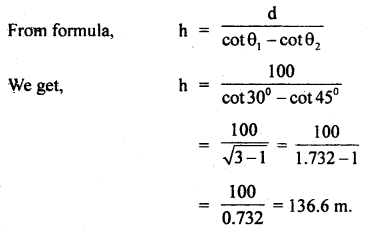
Question 4.
Find the number of air molecules in a room of volume 12 m³. Given 1 mole of air at N.T.P. occupies a volume of 22.4 liters.
Answer:
No. of atoms in I mole of air = N
= 6.023 × 10²³

∴ Also at N.T.P., 1 mole of air occupies 22.4 liters of volume
= 22.4 × 10^-3 m³

∴ No. of molectiles ir 22.4 × 10^-3 m³ volume = 6.023 × 10²³
∴ No. of molecules in 12 m³ volume = \(\frac{6.023 \times 10^{23}}{22.4 \times 10^{-3}}\) × 12
= 3.23 × 10²⁶

Question 5.
(a) Convert ION into dyne using dimensional analysis.
Answer:
Newton (N) and dyne are the S.I. and C.G.S. units of force having dimensional formula [MLT^-2]
∴ a = 1, b = 1, c = – 2

S.I. system
n₁ = 10
M₁ = 1 kg
L₁ = 1 m
T₁ = 1 s

C.G.S. system.
n₂ = ?
m₂ = 1 g
L₂= 1 cm
T₂ = 1 s

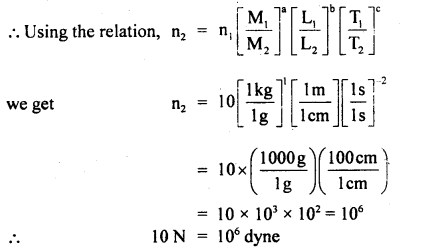
(b) Find the units of length, mass, and time of the unit of force, velocity, and energy are 100 dynes, 10 cms^-1, and 500 erg respectively.
Answer:

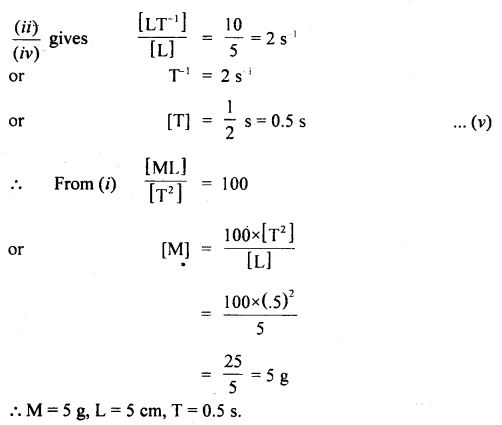
Question 6.
Check the dimensional correctnesïof the relation
V = \(\sqrt{\frac{2 G M}{R}}\)
Answer:
It is done using the principle of homogeneity of dimensions i.e. if the dimensions of each term of both sides of the equation are the same, Then it is dimensionally correct.
Now dimensions of V = [LT^-1].
G = [M^-1 L³ T²]
M = [M]
R = [L]

∴ Dimensions of L.H.S. = [V] = [LT^-1] …(f)
Dimensions of R.H.S = \(\sqrt{\frac{G M}{R}}\)

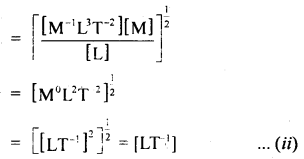
Now from equations (i) and (ii), it is clear that the dimensions of L.H.S = R.H.S, so the given relation is dimensionally correct.

Question 7.
Suppose that the oscillatións of a simple pendulum depend on
(i) mass of the bob (m),
(ii) length of the string (1),
(iii) acceleration due to gravity (g) and (iv) angular displacement
(iv) Dimensionally show which of the above factors here an influence upon the period and in what way?
Answer:
Let t ∝ m^a l^b g^c θ^d
or t = k’ m^a l^b g^c q^d ….(i)
here k’ is a dimensionless constant.

Since q is dimensionless, hence equation (i) reduces to
t = K m^a l^b g^c …(ii)

where K. = k¹.θ^d is another dimensionless constant.
Now writing the dimensional formula of each physical quantity on both sides of equation (ii), we get
[M⁰ L⁰ T^-1] = [M]^a [L]^b [LT²]^c = [M^a L^b-c T^-2c]

Comparing dimensions of


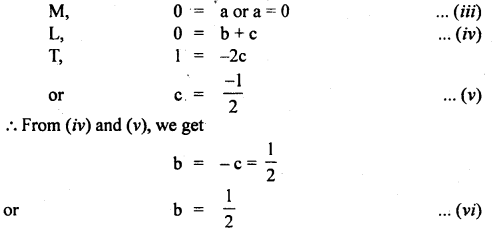
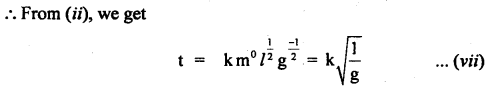
Thus from equation (vii), we see that the period of the pendulum is directly proportional to the square root of the length of string, and inversely proportional to the square root of acceleration due to gravity and is independent of the mass of the bob.

Question 8.
Given that the period T of oscillation of a gas bubble from an explosion underwater depends on P, d, and E, where the symbols are pressure, density, and total energy of the explosion. Find dimensionally a relation for T.
Answer:
Let T ∝p^a d^b E^c
or
T = k p^a d^b E^c …(i)
where k is a dimensionless constant.

Writing dimensional formula of each physical quantity on both sides of equation (i), we get

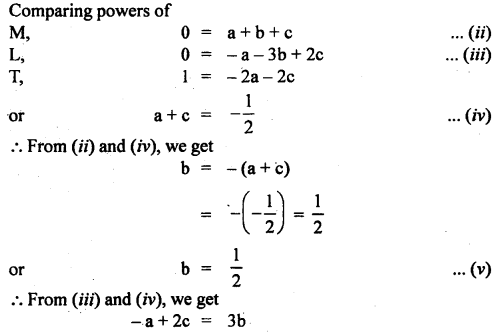
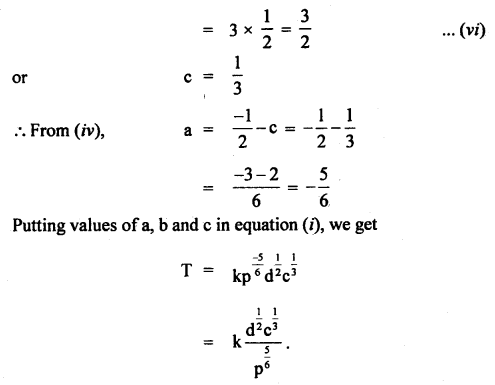
Question 9.
If the velocity of light c, the constant of gravitation G, and Plank’s constant h be chosen as fundamental units, find the value of a gram, a centimeter, and a second in terms of new units of mass, length, and time respectively.
Given c = 3 × 10¹⁰ cms^-1
G = 6.67 × 10^-8 dyne cm² g^-2
h = 6.6 × 10^-27 ergs.
Answer:

Question 10.
Assuming that the mass m of the largest stone that can be moved by a flowing river depends on the velocity y density p and acceleratión due to gravity g. Show that m varies as the sixth power of the velocity of flow.
Answer:
Let, m ∝ v^a
m ∝ρ^bb

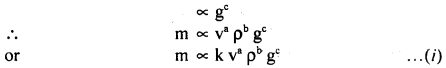
where k is a dimensionless constant.

Writing dimensions of each physical quantity on both sides of equation (i), we get
[M¹ L⁰ T⁰] = [LT^-1] [ML^-3]^b [LT^-2]^c
[M^b L ^a-3b+2c T^-a-2c]

Comparing powers of:

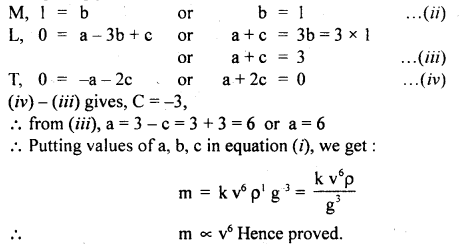
Question 11.
The radius of Earth is 6.37 × 106 m and its average density is 5.517 × 10³ kg m^-3. Calculate the mass of Earth to correct significant figures.
Answer:
M = pV
Here, R = 6.37 × 10⁶ m,
ρ = 5.517 × 10³ kg m³

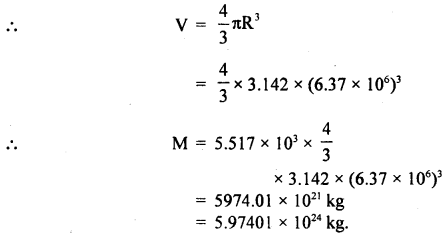
Here R has 3 significant figures and the density has four. Thus the final result should be rounded off to 3 significant figures.

Hence, M = 5.97 × 10²⁴ kg.

Question 12.
The length, breadth, and thickness of a block of metal were measured with the help of Vernier Callipers. The measurements are:
l = (5.250 ± 0.001) cm
b = (3.450 ± 0.001) cm,
t = (1.740 ± 0.001) cm.
Find the percentage error in the volume of the block.
Answer:
The volume of the block is given by:
V = lbt

∴ The relative percentage error in V is given by:

Question 13.
An experiment measures quantities a, b, c, and x is calculated from the relation:
x = ab²/c³
The percentage errors in a, b, c are ± 1%, ± 3%, and ± 2% respectively what is the % error in x?
Answer:

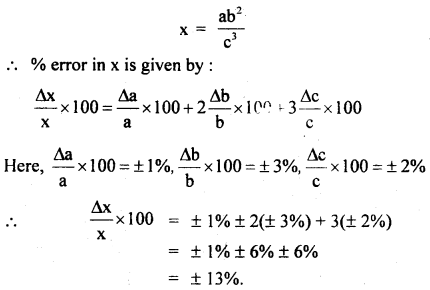
Question 14.
The radius of the proton is about 10^-9 microns and the radius of the universe is about 10²⁸ cm. Name a physical object whose size is approximately halfway between these two extremes on the logarithmic scale.
Answer:
Radius of proton, x₁ = 10^-9 microns = 10^-9 × 10⁶m .
= 10^-15m

Radius of universe, x₂ = 10²⁸ cm = 10²⁶m.

If x be the size halfway between these two extremes on the logarithmic scale is:

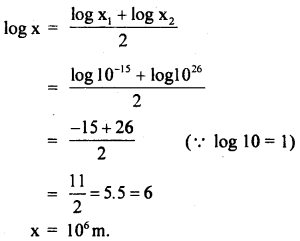
Since 10⁶m is the order of the size of the Earth. So the physical object is Earth.

Question 15.
The velocity v (cms^-1) of a particle is given in terms of time t (s) by the equation y = at + \(\frac{b}{t+c}\). What are the dimensions of a, b and c?
Answer:
v = at + \(\frac{b}{t+c}\).

L.H.S. is velocity, so according to principle of homogeneity t, of dimensions, at and must have the dimensions of \(\frac{b}{t+c}\) velocity.

Question 16.
The young’s modulus (Y) of a material is given by the relation Y = \(\frac{\mathbf{M g L}}{\pi \mathbf{r}^{2} \boldsymbol{l}}\). If the percentage error in W(= mg), L, r and l are 0.5%, 1%, 3% and 4% respectively, what is the percentage error in Y? If the calculated value of Y is 18.79 × 10¹¹ dyne cm^-2, to what value should we round off the result?
Answer:
The total percentage error in Y is given by:

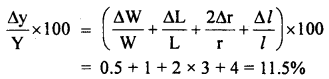
Since Y = 18.79 × 10¹¹ dyne cm^-2, it can be rounded off to
Y = 19 × 10¹¹ dyne cm^-2

The total percentage error in this result is:
\(\frac{19 \times 11.5}{100}\) = 2.2

So, the result of Y can be quoted as (19 ± 2.2) × 10¹¹ dyne cm^-2

Question 17.
The refractive index as measured by relation:
μ = \(\frac{\text { real depth }}{\text { apparent depth }}\) was found to have values 1.29, 1.33, 1.34, 1.35, 1.32, 1.36, 1.30, 1.33.
Find the mean value of μ, the mean value of the absolute error, the relative error, and the percentage error.
Answer:
Mean value of μ

Question 18.
Derive the dimensions of a/b in the relation:
F = a\(\sqrt{x}\) + bt²
where F is the force, x is the distance and t is the time.
Answer:
Here, F= a\(\sqrt{x}\) + bt² …(i)

According to the principle of homogeneity of dimensions, a \(\sqrt{x}\) and bt² should have dimensions of F.

Question 19.
Calculate the number of seconds in a:
(i) day
(ii) year
and express them in orders of magnitude.
Answer:
(i) No.of seconds in a day = 24 × 60 × 60s
= 86400s
= 8.64 × 104s
= 0.864 × 105s
∴ order of magnitude = 5

(ii) No.of seconds in a year = 365 days
= 365 × 0.864 × 105s
= 315360 × 105s
= 31536 × 107s
∴ order of magnitude = 7.

Question 20.
A stone is lying in a fluid stream. The force F acting on it depends on the density of the fluid δ, the velocity of flow v, and the maximum area of cross-section A perpendicular to the direction of flow. Find the relation between the force F and the velocity v.
Answer:
Let, F ∝ ρ^a
∝ v^b
∝ A^c
or
F ∝ p^a v^b A^c
or
F = k p^a v^b A^c …(i)

Now writing the dimensional formula of each physical quantity on both sides of equation (i), we get:
[MLT^-2] = [ML^-3]^a [LT^-1]^b [L²]^c
= [M^a L^-3a+b+2c T^-b] …(ii)

Comparing dimensions of M, L, T on both sides of equation (ii), we get:

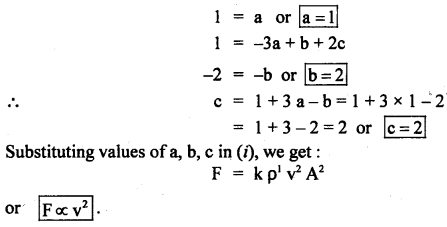
Question 21.
If we suppose the velocity of light (c), acceleration due to gravity (g), and pressure (p) as the fundamental units, then And the dimensional formula of mass in this system of units.
Answer:

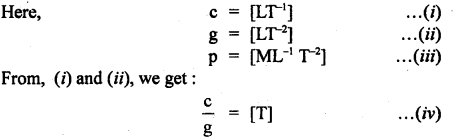
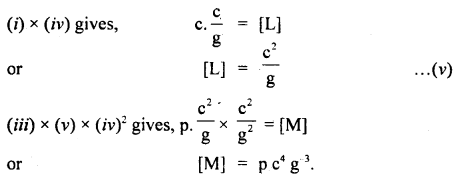
Question 22.
The density p of a piece of metal of a mass m of and volume V is given by the formula, ρ = m/V.
If, m = 325.32 ± 0.0lg
V = 136.41 ± 0.01 cm³.
Find the percentage error in p:
Answer:
Here, m = 325.32g, Δm = 0.01 g
V = 136.41 cm³, ΔV = 0.01 cm³

Question 23.
The specific resistance σ of a circular wire of radius r cm, resistance R Ω and and length L is given by:
σ = \(\frac{\pi r^{2} R}{L}\)
If, r = 0.20 ± 0.02 cm
R = 20 ± 1Ω
L = 80 ± 0.01 cm, then find the % error in σ.
Answer:
% error in σ is given by:

Question 24.
If S² = a t⁴, where S is in meters, t in second, then find the unit of a.
Answer:
Here, S² = a t⁴
According to the principal of homogeneity of dimensions,
at⁴ = m²
∴ a = \(\frac{\mathrm{m}^{2}}{\mathrm{t}^{4}}\) = m² s^-4

Question 25.
Calculate the value of 600m. + 600mm with due regard to the significant digits.
Answer:
Here, because there is no significant digit after the decimal point in 600m, so 600m + 600mm.
= 600m + 600 × 10^-3m
= 600m + 0.600m
= 600.6m = 601m.

Value-Based Type:

Question 1.
The teacher of class XI asked Madan and Prathiva to find the distance of the moon from the Earth. Pratibha said it is impossible to find. But Madan was excited to know. He observed the moon from two diametrically opposite points A and B on Earth. The angle q subtended at the moon by the two directions of observation is 1°54′. Given the diameter of the Earth to be about (1.276 × 10⁷ m).
(i) Which values arc depicted by Madan?
Answer:
The values depicted by Madan are :
(a) Curiosity
(b) Sincerity
(c) Willing to know and implement the scientific ideas.

(ii) Which mathematical concept is used in the above problem?
Answer:
Parallax method

(iii) Compute the distance of the moon from the Earth?
Answer:

We have

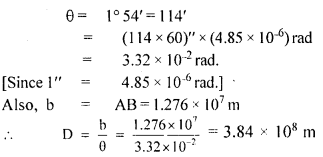
Question 2.
Muesli went to London to his uncle who is a doctor over there. He found that the currency is quite different from India. He could not understand the pound and how it is converted into rupees. He asked an English man that how far is central London from here.

He replied that it is about 20 miles. Mukesh was again confused as he never used these units in India. When his uncle came back from his clinic he curiously inquired all about it. His uncle told him about the unit system used in England. He explained that here F.P.S system is used.

It means distance is measured in the foot, Mass in the pound, and time in seconds. But in India, it is an MKS system.
(i) What values are depicted by Mukesh?
Answer:
(a) Curiosity
(b) Willing to know
(c) Intelligence

(ii) How many types of unit systems are there?
Answer:
The unit system is:
(a) CGS (centimeter, gram and second) system
(b) FPS (foot, pound and second) system
(c) MKS (meter, kilogram, and second) system

Question 3.
Two friends Sachin and Dinesh are confused as a book with many printing errors contains four different formulas of the displacement ‘y’ of a particle undergoing a certain periodic motion.
(a) y=asin 2πt/T
(b) y = asinvt

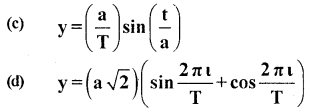
[a = Maximum displacement of the particle,
v = Speed of the particle, T = time-period of motion]

Sachin told that he has no idea whereas Dinesh ruled out the wrong formulas on dimensional grounds.
(i) which values are displayed by Dinesh?
Answer:
the values displayed by Dinesh are:
(a) Sincerity
(b) Curiosity
(c) application of knowledge

(ii) which one of the above is correct? Give justification to support your answer.
Answer:


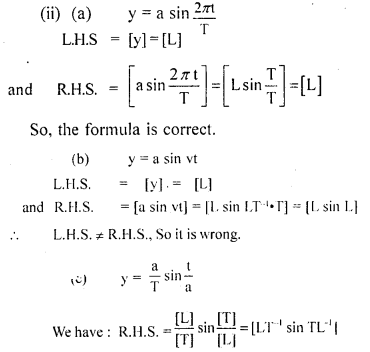
L.H.S = R.H.S ; Hence the equation is correct.