Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 3 Motion in a Straight Line. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.
Class 11 Physics Chapter 3 Important Extra Questions Motion in a Straight Line
Motion in a Straight Line Important Extra Questions Very Short Answer Type
The Velocity Calculator is a handy physics tool to quickly get your answer.
Question 1.
Can a moving body have relative velocity zero with respect to another body? Give an example.
Answer:
Yes, two trains running on two parallel tracks with the same velocity in the same direction.
Free Projectile Motion Calculator – calculate projectile motion step by step.
Question 2.
Can there be motion in two dimensions with acceleration in only one dimension?
Answer:
Yes, projectile motion.
Question 3.
Is it true that a body is always at rest in a frame that is fixed to the body itself?
Answer:
Yes.
Question 4.
Tell under what condition a body moving with uniform velocity can be in equilibrium?
Answer:
When the net force on the body is zero.
Question 5.
What does the speedometer records: the average speed or the instantaneous speed?
Answer:
It records (or measures) the instantaneous speed.
Question 6.
Can an object be accelerated without speeding up or slowing down? Give examples,
Answer:
Yes, circular motion.
Question 7.
Is it possible to have the rate of change of velocity constant while the velocity itself changes both in magnitude and direction? Give an example.
Answer:
Yes, in projectile motion.
Question 8.
Which motion is exactly represented by Δs = vΔt?
Answer:
It Represents motion with uniform velocity.
Question 9.
In which frame of reference is the body always at rest?
Answer:
The body is always at rest in the frame attached to it i. e. inertial frame of reference.
Question 10.
What is common between the two graphs shown in figs, (a) and (b)?
Answer:
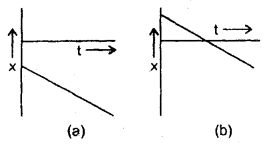
Both these graphs represent that the velocity is negative.
Question 11.
What is common between the two graphs shown in figs, (a) and (b)?
Answer:
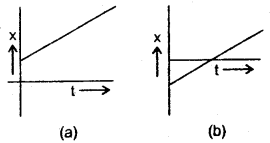
Both these graphs represent that velocity is positive.
Question 12.
What is meant by a point object in Physics?
Answer:
An object is said to be a point object if its dimensions are very small as compared to the distance covered by it.
Question 13.
The displacement of a body is zero. Is the distance covered by it is necessarily zero?
Answer:
No.
Question 14.
Which of the velocity or speed is measured by the speedometer of a vehicle?
Answer:
Speed.
Question 15.
Can you think of a situation where a body falling under gravity has constant velocity? Give example.
Answer:
Yes, the terminal velocity of a body.
Question 16.
Give an example of a motion which even though is accelerated motion yet it is called uniform motion.
Answer:
Uniform circular motion.
Question 17.
How many-dimensional motion does the following have?
(a) Train moving fast on its track.
Answer:
One dimensional motion.
(b) A lizard moving on a wall in a room.
Answer:
Two-dimensional motion.
(c) Kite flying in the sky.
Answer:
and
(d) Bee flying in a closed room.
Answer:
Three-dimensional motion.
Question 18.
When is the average velocity over an interval of time becomes equal to instantaneous velocity?
Answer:
When the velocity is constant.
Question 19.
A coolie carries a bag of luggage from one side of a platform to another side on the same platform. How far vertically the load is shifted?
Answer:
Zero.
Question 20.
The displacement of a body is proportional to the square of time along a straight line. Is the body moving with constant velocity or constant acceleration?
Answer:
It is moving with constant acceleration.
Question 21.
When the train in which you are sitting starts moving by the side of another train without jerks, you find that the other train is moving but when you look to the platform you find that your train is moving. Name the phenomenon responsible for such a motion.
Answer:
Relative velocity is the phenomenon responsible for such a motion.
Question 22.
Under what condition the magnitude of the average velocity of a particle is equal to the average speed?
Answer:
The magnitude of the average velocity of a particle is equal to the average speed if it moves with constant velocity.
Question 23.
Two particles A and B are moving along the same straight line with B being ahead of A. Velocities remaining unchanged, what would be the effect on the magnitude of relative velocity if A is ahead of B? ’
Answer:
The magnitude of the relative velocity will remain the same i.e. no effect on its magnitude.
Question 24.
Define the speed of the object.
Answer:
The speed of an object is defined as the distance covered by it per unit of time.
Question 25.
Why the speed of an object cannot be negative?
Answer:
The speed of an object cannot be negative because the distance can never be negative.
Question 26.
Can a body have zero velocity and still accelerating?
Answer:
Yes.
Question 27.
Can the direction of the velocity of a body change, when acceleration is constant?
Answer:
Yes.
Question 28.
Is the acceleration of a car is greater when the accelerator is pushed to the floor or when the brake pedal is pushed hard?
Answer:
The acceleration of the car is greater when the brake pedal is pushed hard because the car comes to rest suddenly i. e. the rate of change of velocity of the car is large in this case, so the acceleration.
Question 29.
The displacement is given by x = 2 + 4t + 5t2. Find the value of instantaneous acceleration.
Answer:
a = \(\frac{\mathrm{d}^{2} \mathrm{x}}{\mathrm{dt}^{2}}\) = 10
Question 30.
A stone is thrown vertically upwards from the surface of Earth. What is the direction of the velocity and acceleration of the stone?
(a) on its upward motion
Answer:
Velocity is vertically upward and acceleration is vertically downward.
(b) on its downward motion?
Answer:
Both velocity and acceleration are vertically downward.
Question 31.
Can Earth be regarded as a point object if only the orbital motion of Earth around the Sun is considered? Why?
Answer:
Yes. This is because the size of Earth is very small as compared to the size of the orbit of the Earth around the Sun.
Question 32.
The motion of two persons is shown by two straight lines on a displacement time graph intersecting each other at a certain point. What information do you get from the point of intersection?
Answer:
This means that the two persons cross each other at a certain place at a given instant of time.
Question 33.
Following two equations represents the x – t relation for the motion of an objects.
x (t) = x(0) + v(0)t + \(\frac{1}{2}\) at2
and x(t) = v(0)t + \(\frac{1}{2}\) at2
What is the difference between them?
Answer:
The first equation is a more general form of motion as it contains information regarding the initial position of the object.
Question 34.
Can the speed of a body change if its velocity is constant? Why?
Answer:
No, the speed of a body cannot change if its velocity is constant which means that both the magnitude and direction of velocity do not change. The magnitude of velocity is speed, so speed cannot change.
Question 35.
If the instantaneous velocity of a particle is zero, will its instantaneous acceleration be necessarily zero?
Answer:
No.
Question 36.
What is the shape of the displacement time graph of a particle having an average velocity equal to its instantaneous velocity?
Answer:
In this case, the velocity is uniform, so the x – t graph is a straight line.
Question 37.
Can there be a two-dimensional motion with acceleration in one dimension only? Give example.
Answer:
Yes, a projectile motion which is two-dimensional one has acceleration only in one dimension i.e. vertically downward.
Question 38.
Under what condition will the distance and displacement of a moving object will have the same magnitude?
Answer:
The distance and displacement of a moving object will have the same magnitude when it is moving with uniform velocity along a straight line.
Question 39.
Under what condition an object in motion cannot be considered a point object?
Answer:
A moving object cannot be considered as a point object if its size is not negligible as compared to the distance travelled by it.
Question 40.
Define a point object.
Answer:
It is defined as an object having dimensions (length, breadth, thickness etc.) very small as compared to the distance covered by it.
Question 41.
Is the following graph possible for the motion of a particle moving along a straight line?
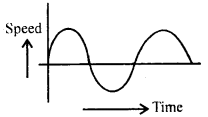
Answer:
No.
Question 42.
Explain why the graph in the above question is not possible?
Answer:
This is because the speed for a given time is negative and speed is always positive.
Question 43.
Why the following graph is not possible for the motion of a particle moving along a straight line?
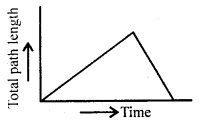
Answer:
This is because here the path length decreases with time while it must either increase or must remain constant.
Question 44.
What happens to kinematic equations under time reversal?
Answer:
The kinematic equations of motion don’t change in the form under time reversal i.e. if t is replaced by -t.
Question 45.
What happens to the uniform motion of a body when it is given an acceleration at right angles to its motion?
Answer:
The body will come in a circular motion when it is given an acceleration at right angles to its motion.
Question 46.
To deal with physical phenomena, we consider objects even as big as Sun a point objects. Can you name physical phenomena in which Earth cannot be taken as a point object?
Answer:
The occurrence of solar or lunar eclipse does not allow Earth to be taken as a point object otherwise the phenomena cannot be explained.
Question 47.
The average velocity of a body moving with uniform acceleration is given by \(\frac{1}{2}\) (u + v). Ii the acceleration changes from point to point can the average velocity be still given by this expression? Give reason.
Answer:
No, the average velocity cannot be given by \(\frac{1}{2}\) (u + v) in case the acceleration varies from point to point i.e. if it is not uniform. This is because the slope of the v-t graph does not remain the same at all points.
Question 48.
Acceleration is defined as the rate of change of velocity. Suppose we call the rate of change of acceleration SLAP. Then (i) What is the unit of SLAP.
Answer:
SLAP = Acceleration/time (By definition).
∴ Its unit will be = \(\frac{\mathrm{ms}^{2}}{\mathrm{~s}}\) = ms-3.
(ii) How can you calculate instantaneous SLAP?
Answer:
Average SLAP = \(\frac{\Delta \mathrm{a}}{\Delta \mathrm{t}}\)
∴ Instantaneous SLAP = Limiting value of average SLAP
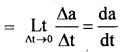
Question 49.
Why is the time stated twice in stating acceleration?
Answer:
Since acceleration is the double rate of change of displacement
i. e. a = \(\frac{\mathrm{d}^{2} \mathrm{x}}{\mathrm{dt}^{2}}\), so time is stated twice in stating acceleration.
Question 50.
Separate the following in one, two and three-dimensional motion :
(a) a kite flying on a windy day.
(b) an insect crawling on a globe.
(c) a carom coin rebounding from the side of the board,
(d) a planet revolving around its star.
(e) the motion of a boat.
(f) the motion of a dropped body.
(g) the motion of a tennis ball.
(h) a charged particle moving under an electric field.
(i) movement of a saw while cutting wood.
(j) molecular motion.
(k) a charged particle moving under a magnetic field.
Answer:
- One dimensional motion : (e), (f), (i)
- Two dimensional motion : (b), (c), (d), (g), (h), (k).
- Three dimensional motion : (a), (j).
Motion in a Straight Line Important Extra Questions Short Answer Type
Question 1.
Prove that the average velocity of a particle over an interval of time is either smaller than or equal to the average speed of the particle over the same interval.
Answer:
Average velocity is defined as the ratio of the total displacement to the total time. Average speed is defined as the ratio of the total distance to the total time. Since displacement is less than or equal to the distance, therefore the average velocity is less than or equal to the average speed.
Question 2.
Two trains each of the length 109 m and 91 m are moving in opposite directions with velocities 34 km h-1 and 38 km h-1 respectively. At what time the two trains will completely cross each other?
Answer:
Let l1, l2 be the lengths of the two trains.
v1, v2 be their velocities respectively.
∴ l1 = 109m, l2 = 91 m, v1 = 34kmh-1, v2 = 38kmh-1.
As the trains are moving in opposite directions so relative velocity of the trains is given by
v1 – (- v2) = v1 + v2
= 34 + 38 = 72 kmh-1
= 72 × \(\frac{5}{18}\) = 20 ms-1
Total distance to be covered by the two trains in crossing each other
= l1 + l2= 109 + 91 = 200 m
If t be the time taken in crossing, then t can be calculated using the relation
x = vt
or
t = \(\frac{200}{20}\) = 10s
Question 3.
Ambala is at a distance of 200 km from Delhi. Ram sets out from Ambala at a speed of 60 km h-1 and Sham set out at the same time from Delhi at a speed of 40 km h-1. When will they meet?
Answer:
S = 200 km. Let VR and vs be the speeds of Ram and Sham respectively moving in opposite directions.
∴ vR = 60 kmh-1, vS = 40 kmh-1.
∴ Relative velocity of Ram w.r.t. Sham is
VRS = VR – (- VS)
= VR + VS
= 60 + 40 = 100 kmh-1
If t = time after which they will meet, then
t = time taken in covering 200 km distance with VRS
i.e. t = \(\frac{200}{v_{\mathrm{RS}}}=\frac{200 \mathrm{~km}}{100 \mathrm{kmh}^{-1}}\) = 2h.
∴ Time after which they meet = 2h.
Question 4.
A car travelling at a speed of 60 km h-1 on a straight road is ahead of a scooter travelling at a speed of 40 km h-1. How would the relative velocity be altered if the scooter is ahead of the car?
Answer:
vc = speed of car = 60 kmh-1
vs = speed of scooter = 40 kmh-1
vcs = relative velocity of car w.r.t. scooter
= vc – vs
= 60 – 40
= 20 kmh-1
Similarly vsc = relative velocity of scooter w.r.t. car
= vs – vc
= 40 – 60
= – 20 kmh--1
Thus we conclude that the magnitude of the relative velocity is the same in both cases but the direction of relative velocity is reversed if the scooter is ahead of the car.
Question 5.
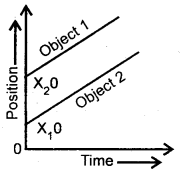
Draw the position-time graphs for two objects initially occupying different positions but having zero relative velocity.
Answer:
The positive T time graphs for two objects initially occupying different positions but having zero relative velocity are parallel to each other as shown in Fig.
Question 6.
A ball is thrown vertically upward with a velocity of 20 ms-1. It takes 4 seconds to return to its original position. Draw a velocity-time graph for the motion of the ball and answer the following questions:
At which point P, Q, R, the stone has :
(a) reached its maximum height.
(b) stopped moving?
Answer:
Let P represent the initial position at the time when the ball is thrown vertically upward.
Q represents the highest point reached by the ball.
R represents the original position of the ball after 4 seconds.
Thus the velocity-time graph for the motion of the ball is as shown in Fig.
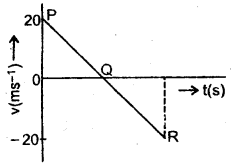
(a) We know that at the highest point, the velocity of the object is zero. So stone will reach its maximum height corresponding to point Q.
(b) The stone has stopped moving at point Q because at Q, v = 0.
Question 7.
“It is the velocity and not the acceleration which decides the direction of motion of a body.” Justify this statement with the help of a suitable example.
Answer:
The direction of velocity is always in the direction of motion of the body whereas the direction of acceleration may or may not be in the direction of motion of the body. Thus we conclude that it is the velocity that decides the direction of motion of the body.
Example: When a ball is thrown vertically upwards, the direction of motion of the ball and velocity is the same i.e. vertically upwards. On the other hand, the acceleration due to gravity on the ball acts vertically downwards i.e. opposite to the direction of motion of the ball.
Question 8.
Two buses A and B starting from the same point move in a mutually perpendicular direction with speeds uA km h-1 and uB km h-1 respectively. Calculate the relative velocity of A w.r.t B.
Answer:
Since uA and uB are in mutually perpendicular directions, they will cover uA and uB km in one hour respectively. Thus if v km be the separation between them in one hour,
Then v = \(\sqrt{\mathrm{u}_{\mathrm{A}}^{2}+\mathrm{u}_{\mathrm{B}}^{2}}\)
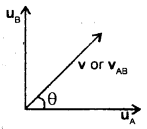
Thus if vAB be the relative speed of A w.r.t. B, then
vAB = \(\sqrt{\mathrm{u}_{\mathrm{A}}^{2}+\mathrm{u}_{\mathrm{B}}^{2}}\) kmh …(1)
If θ be the direction of vAB w.r.t. uA, Then
tan θ = \(\frac{u_{A}}{v_{A B}}=\frac{u_{A}}{\sqrt{u_{A}^{2}+u_{B}^{2}}}\) …(2)
Thus, equations (1) and (2) give the magnitude and direction of relative velocity of A w.r.t. B.
Question 9.
A draw velocity-time graph for a body which
(i) accelerates uniformly from rest,
Answer:
The required velocity-time graph is shown in Fig. here
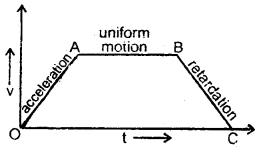
OA part of the graph represents the uniformly accelerated motion of the body.
(ii) then moves with a uniform velocity and
Answer:
AB part of the graph represents motion with uniform velocity.
(iii) finally retarded uniformly.
Answer:
BC part of the graph represents motion with uniform retardation of the body.
Question 10.
From a velocity-time graph, how do you calculate the average acceleration of a moving body?
Answer:
The slope of the velocity-time curve gives the acceleration of the body. For this purpose, we take a small interval of time Δt and a corresponding change in velocity Δv such that Δt = t2 – t1 and Δv = v2 – v1. Over a very small interval of time Δt, arc AB may be considered as a chord AB, then.
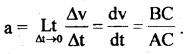
Question 11.
State whether the following two graphs in Fig. here represent the same type of motion or not. Name the motion of the particle.
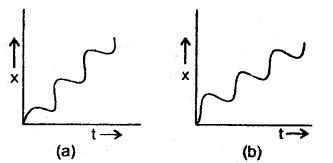
Answer:
Yes. Both of these graphs represent the same type of motion. The motion of the particle represented by these graphs is non-uniform motion i.e. the particle is moving with variable velocity.
Question 12.
Draw the velocity-time graph for an object moving with uniform velocity. What does it show for t < 0?
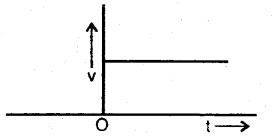
Answer:
As the object moves with uniform velocity, the magnitude and direction of its velocity remain the same at all points of its path. Thus v – t graph’ is a straight line parallel to the time axis as shown in Fig. here.
For t < 0, the v – t graph shows that the object is at rest till t = 0.
Question 13.
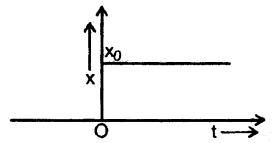
The displacement time graph of a body is shown in the figure below. What does the curve for t < 0 and t > 0 show?
Answer:
The line ∥ to t – axis in fig. shows that the object is at rest t ∥ t = 0. For t > 0, it shows that it is still at rest but at some another poi it at a distance XQ from the point for t < 0.
Question 14.
Distinguish between one, two and three-dimensional motion.
Answer:
The motion of an object along a straight line in a fixed direction is called one-dimensional motion.
- The motion of an object in a plane is called two-dimensional motion
- The motion of an object in space is called three-dimensional motion
Question 15.
A ball thrown upward reaches a height and comes bad downward. Out of the following statements, which one is true for displacement, velocity and acceleration.
(a) It varies continuously but never changes the sign.
(b) It varies continuously with the maximum, in the beginning, being zero at the top.
(c) It remains constant throughout the course of the journey.
(d) It only changes the sign when the ball is at the top.
Answer:
- Statement (a) is true for displacement as it varies from starting
- Statement (b) is true for velocity as it is maximum at the time o projecting the ball and becomes zero at the highest point i.e. top.
- Statement (c) is true for acceleration as it is always constant throughout the course of the journey and is equal to ‘g’.
Question 16.
Derive the expression for the time taken by a body dropped from a height h to reach at Earth.
Answer:
Here,
initial velocity, u = 0
acceleration, a = g
distance covered, S = h
Let t = time taken
Using the relation
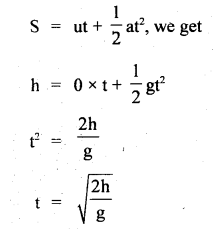
Question 17.
In which of the following cases, the body may be considered a point object:
(a) A railway carriage moving without jerks between two stations.
(b) A monkey sitting on the shoulder of a cyclist moving smoothly in a circular track.
1 A beaker tumbling down the edge of a table, A spinning cricket ball that turns sharply on hitting the ground.
Answer:
(a) and (b) as the distance moved by the bodies is much larger; the size of the body.
Question 18.
What do you understand by positive and negative time?
Answer:
The origin of time is called zero time. The instant of time which is after the origin of time is called positive time and the instant of, which is taken before the origin of time is called negative time.
Question 19.
If the displacement time graph of a particle is parallel to the displacement axis (b) the time axis, what will be the velocity particle? Why?
Answer:
(a) When the displacement-time graph is parallel to the displacement axis, the velocity of the particle is infinity.
We know that velocity = \(\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}\)
when the graph is parallel to the displacement axis, then Δt = 0, so velocity = infinity.
(b) When the displacement-time graph is parallel to the time axis, the velocity of the particle is zero as in this case Δx = 0.
Question 20.
An object is in uniform motion along a straight line. What will be its position-time graph if
(a) x0 = +ve, v = +ve,
(b) x0 = +ve, v = – ve,
(c) x0 = – ve, v = +ve,
(d) x0 = – ve, v = – ve.
The letters x0 and v represent the position of the object at time t = 0 and the uniform velocity of the object respectively.
Answer:
The position of an object at any time t moving with a uniform velocity along a straight line is given by
x = x0 + vt ….(1)
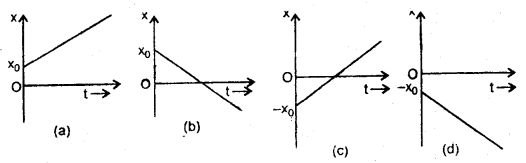
(a) If X0 > 0, v > 0 i.e. both positive, then the position-time graph is as shown in Fig. (a).
(b) If X0 = +ve, v = – ve, then the x – t graph is as shown in Fig. (b).
(c) If X0 = – ve, v = +ve, then the x – t graph is as shown in Fig. (c).
(d) If both x0 and v are – ve, then the x -t graph is as shown in Fig. (d).
Question 21.
Define displacement. What are its characteristics?
Answer:
It is defined as the change in the position of an object in a particular direction.
Characteristics of displacement:
- It is a vector quantity.
- It has units of length.
- The magnitude of displacement is called distance.
- The diode valve curve between voltage and current is quite like curve ABCD.
Question 23.
What are the important points about the uniform motion?
Answer:
The following are some important points about the uniform motion:
- The velocity in uniform motion does not depend upon the time interval (t2 – 1,).
- The velocity in uniform motion is independent of the choice of origin.
- The average and the instantaneous velocities have the same value in uniform motion.
- No force acts on the object having uniform motion.
- Velocity is taken to be positive when the object moves toward the right of the origin and it is taken -ve if an object moves toward the left of the origin.
Question 24.
A car is being driven at a uniform velocity u. The driver suddenly puts his foot on the accelerator and the speed increases to v. Unfortunately after that his brakes failed. Show his velocity-time graph.
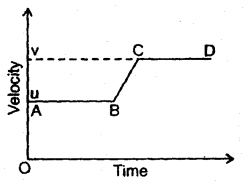
Answer:
Initially, the graph will be parallel to the time axis and is represented by AB when the velocity is uniform. Thereafter it is accelerated and its velocity becomes v. The car will then move with this velocity represented by CD.
Question 25.
Draw position-time graphs of two objects moving along a straight line when their relative velocity is (a) zero and (b) non-zero.
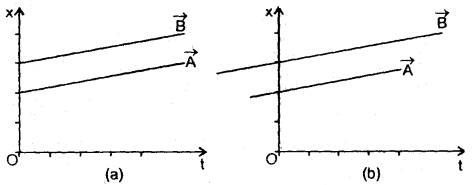
Answer:
The motion of two objects moving along a straight line can be represented by two parallel lines on the position-time graph.
In case of zero relative velocity the two vectors \(\vec{A}\) and \(\vec{B}\) will have the same magnitude as shown in fig. (a) and when the relative velocity is non-zero, the length of the two vectors i.e. the magnitude of vectors is different even though they are parallel and is shown in fig.(b).
Question 26.
Prove that the distance travelled by an object in nth second is given by
Snth = u + \(\frac{a}{2}\) (2n – 1)
Answer:
Derivation: Let Sn and Sn-1 be the distances covered by an object in n and n-1 seconds respectively.
Let u = its initial velocity
a = acceleration produced in the object
∴ Using the relation
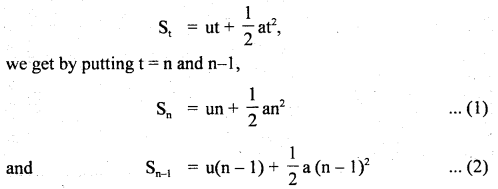
If Snth is the distance covered by the object in nth second. Then
Snth = Sn – Sn-1
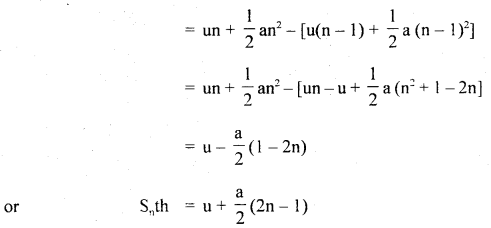
Hence proved.
Question 27.
Is it possible that the velocity of an object be in a direction other than the direction of acceleration? When?
Answer:
Yes, when a body moves in a circular path, then the direction of the velocity is along the tangent to the point on the circle and the acceleration is always towards its centre.
Question 28.
Is the rate of change of acceleration with the time important to describe the motion of a body? Why?
Answer:
No, because it is observed that only velocity and acceleration are sufficient to understand and explain the motion of a body.
Question 29.
Explaining with an example, why does a person sitting in a train think that the other train is at rest when both are moving on parallel tracks with the same speed and in the same direction?
Answer:
This is because the relative velocity of the train in which the person is sitting w.r.t. the other train is zero.
e.g. Let two trains A and B are moving along east with a velocity of 50 km/h i.e. vA = vB = 50 kmh1.
∴ relative velocity of A w.r.t. B is given by
VAB = vA – vB = 50 – 50 = 0.
Question 30.
Can a body be said to be at rest as well as in motion? Explain.
Answer:
Yes, both rest and motion are relative terms. A body at rest w.r.t. one object may be in motion w.r.t. another object, e.g. a person sitting in a moving train is at rest w.r.t. other passengers in the train but at the same time, he is in motion w.r.t. the surroundings (trees or buildings) on the side of the track.
Motion in a Straight Line Important Extra Questions Long Answer Type
Question 1.
Define the following terms :
(a) speed
Answer:
Speed : It is defined as the time rate of change of position
i. e. distance of an object.
i.e. Speed = \(\frac{\text { Distance travelled by the object }}{\text { Time taken }}\)
(b) uniform speed
Answer:
Uniform Speed: An object is said to be moving with uniform speed if it covers equal distances in equal small intervals of time.
(c) variable speed
Answer:
Variable Speed: An object is said to be moving with variable speed if it covers equal distances in unequal small intervals of time.
(d) average speed
Answer:
Average Speed: It is used to measure the variable speed of an object.
It is defined as the ratio of the total distance travelled by the object to the total time taken.
∴ vav = \(\frac{\text { Total }}{\text { Total time taken }}\)
(e) instantaneous speed
Answer:
Instantaneous Speed: It is defined as the speed of an object at a given instant of time. It is denoted by vins.
∴ If Δs be the distance covered by an object in a small time interval Δt s.t. Δt → 0,
Then
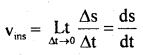
Thus in the case of the uniform motion of an object, the instantaneous speed is equal to its uniform speed.
(f) velocity
Answer:
Velocity: It is defined as the time rate of change of displacement of an object.
(g) uniform velocity
Answer:
Uniform Velocity: An object is said to be moving with uniform velocity if it undergoes equal displacements in equal intervals of time however small these intervals may be.
(h) variable velocity
Answer:
Variable Velocity: An object is said to be moving with variable velocity if either its magnitude (i.e. speed) or its direction or both change with time.
(i) uniform motion
Answer:
Uniform Motion: An object is said to be in uniform motion if it undergoes equal displacements in equal intervals of time which may be very small.
(j) average velocity in uniform
Answer:
Average Velocity in Uniform Motion: The velocity of an object in uniform motion may be defined as the ratio of the .displacement of the object to the total time interval for which the motion takes place.
i.e. v = \(\frac{x_{2}-x_{1}}{t_{2}-t_{1}}\)
(k) relative velocity motion
Answer:
Relative Velocity: The relative velocity of a moving object with respect to another object is defined as the rate of change of relative position of one object w.r.i. another object.
Or
It is the velocity with which one object moves with respect to another object.
(l) instantaneous velocity
Answer:
The instantaneous velocity of an object: It is defined as the velocity of an object at any instant of time or any point on its path.
Or
It is defined as the limiting value of the average velocity of the object as Δt → 0.
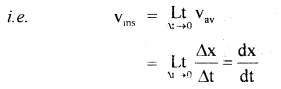
(m) acceleration
Answer:
Acceleration: It is defined as the time rate of change of velocity of an object. It is a vector quantity.
(n) retardation
Answer:
Retardation: It is defined as the negative acceleration produced in the object.
(o) variable acceleration
Answer:
Variable Acceleration: An object is said to be moving with variable acceleration if its velocity changes by unequal magnitudes in equal intervals of time.
(p) average acceleration
Answer:
Average Acceleration: It is defined as the ratio of change in velocity in a given time interval to the total time taken.
(q) uniform acceleration
Answer:
Uniform Acceleration: An object is said to be moving with uniform acceleration if it undergoes equal changes in velocity in equal intervals of time.
(r) instantaneous acceleration.
Answer:
Instantaneous Acceleration: It is defined as the acceleration of an object at a particular instant of time or at a particular point on its path.
Or
It may be defined as the limiting value of the average acceleration in a small time interval around that instant when the time-interval tends to zero.
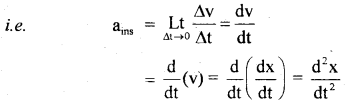
Question 2.
Explain the importance of the position-time graph.
Answer:
1. The importance of a position-time graph is that its slope gives the velocity of the object in uniform motion.
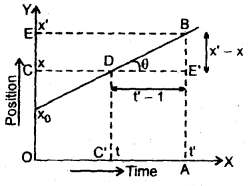
Let us consider the position-time graph of an object moving with uniform velocity represented by the line DB making angle 0 with the time axis. Let the coordinates of D and B be (x, t) and (x’, t’ ) respectively. Let BA and DC’ be perpendiculars drawn from B and D respectively on the time axis and BE and DC be perpendiculars on the y-axis from B and D.
Now BE’ = CE = x’ – x
and C’A = t’ – t = DE’
Then velocity = \(\frac{x^{\prime}-x}{t^{\prime}-t}=\frac{B E^{\prime}}{D E^{\prime}}\) = tanθ
So, velocity v = slope of position-time graph.
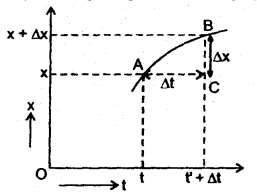
2. The position-time graph for a stationary object is a straight line parallel to the time axis. Here the slope of the curve is zero, which means the object is stationary as v = 0.
3. In the case of variable velocity the position time curve is not a straight line. In this case, the slope of the curve gives the average velocity
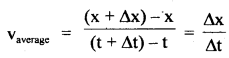
= slope or chord AB when Δt → 0,
then the slope of curve gives the instantaneous velocity.
Instantaneous velocity =
![]()
Thus the position-time graph gives information about velocity.
Question 3.
Derive relations :
(i) v = u + at
Answer:
v = u + at:
Derivation: By def. of acceleration, we know that
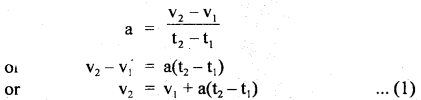
where v1 and v2 are the velocities of an object at times t1 and t2 respectively.
If v1 = u (initial velocity of the object) at t1 = 0
v2 = v (final velocity of the object) at t2 = t
Then (1) reduces to v = u + at
Hence derived.
(ii) v2 – u2 = 2as
Answer:
Derivation : We know that acceleration is given by a =\(\frac{v_{2}-v_{1}}{t_{2}-t_{1}}\) , where v1 and v2, t1 and t2 are as in (1).
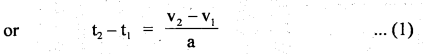
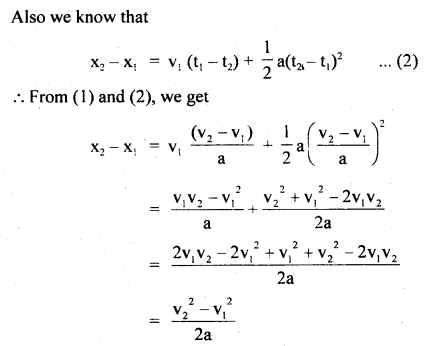
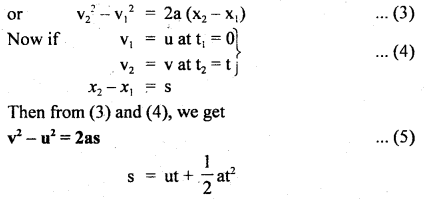
(iii) s = ut + \(\frac{1}{2}\) at2.
Answer:
Derivation:
Let x1, V1 = position and velocity of the object at time t1.
x2, v2 = position and velocity of the object at time t2.
a = uniform acceleration of the object.
Also Let vav = average velocity in t2 – t1 interval
∴ By definition
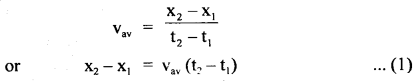
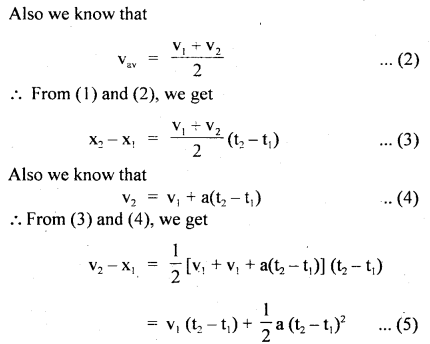
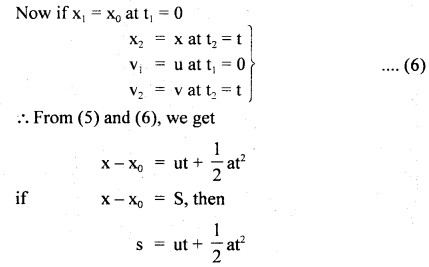
Hence derived.
Numerical Problems:
Question 1.
In a car race, car A takes a time t s less than car B and finishes the finishing point with a velocity v more than that of car B. Assuming that the cars start from rest and travel with constant acceleration a, and a respectively show that
v = t\(\sqrt{\mathbf{a}_{1} \mathbf{a}_{2}}\)
Answer:
Let v1, v2 be the finishing velocities of car A and car B respectively. Let t1, t2 be the finishing time-intervals for car A and car B respectively.
d = distance travelled by both cars.
∴ according to the statement
V = v1 – v2 ….(i)
t = t2 – t1 …(ii)
Let d = distance covered during a race by each car
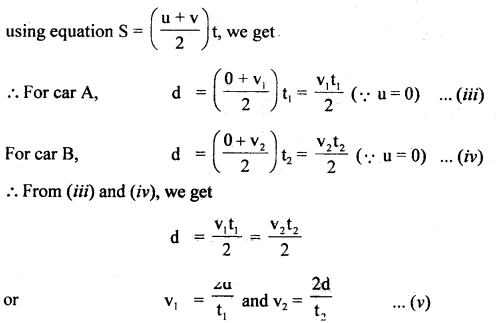
Also using equation
s = ut + \(\frac{1}{2}\) at2, we get
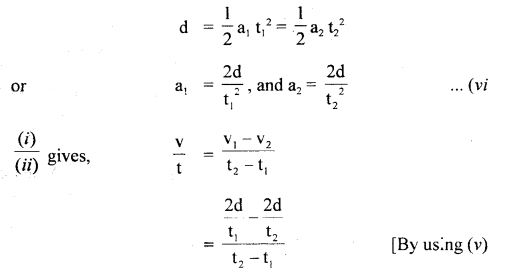
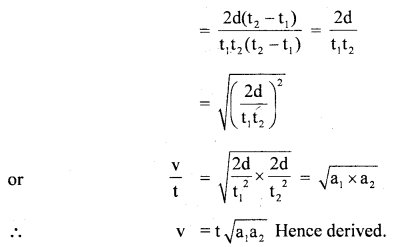
Question 2.
A car accelerates from rest at a constant rate a, for sometime after which it decelerates at a constant rate B to come to rest. If the total time elapsed is t s, then calculate
(a) maximum velocity reached.
(b) total distance travelled.
Answer:
The given situation is shown in fig. below:
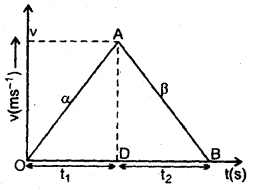
Let t1 and t2 be the times of acceleration and deceleration respectively of the car.
If t = total time of journey,
then t = t1 + t2 … (i)
Also let v = maximum velocity reached
(1) For accelerated motion, using equations, v = u + at, we get
v = 0 + αt1
or
v = αt1 … (ii)
(2) For decelerated motion,
here, u = v, final velocity is zero.
∴ 0 = v + (- β)t2
v = βt2 …(iii)
∴ From (ii) and (iii), we get
αt1 = βt2
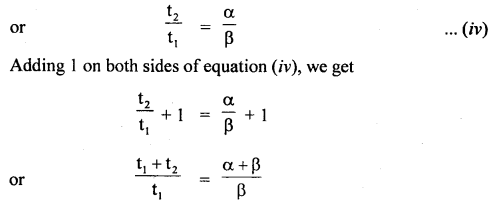

Question 3.
The driver of a train moving at a speed v1 sights another train at a distance d ahead of hint moving in the same direction with a slower speed v2. He applies brakes and gives a constant deacceleration ‘a’ to his train. Show that there will be no collision if
d > \(\frac{\left(\mathbf{v}_{1}-\mathbf{v}_{2}\right)^{2}}{2 \mathbf{a}}\)
Answer:
Let the collision be just avoided i.e. the rear train comes to rest after travelling a distance d with a declaration ‘a’.
the initial speed of 1 st train = v1
the initial speed of 2nd train = v2
If u = initial relative speed of 1 st w.r.t. 2nd train, then
u = v1 – v2
Final velocity of rear train v = 0
∴ using equations, v2 – u2 = 2as, we get
0 – (v1 – v2)2 = 2(- a) d (Here a = -a, s = d.)
d = \(\frac{\left(\mathbf{v}_{1}-\mathbf{v}_{2}\right)^{2}}{2 \mathbf{a}}\)
Thus there will be no collision, if
d > \(\frac{\left(\mathbf{v}_{1}-\mathbf{v}_{2}\right)^{2}}{2 \mathbf{a}}\)
Question 4.
A stone is dropped from the top of a tower and after one second, another stone is dropped from a point 20 m below the top. If both the stones reach the ground at the same time, calculate the height of the tower (take g = 10 mf2).
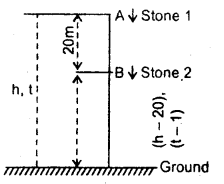
Answer:
The given situation is shown in fig.
Let t = time taken by the first stone to reach the ground
h = height of the tower
u1 = initial velocity O
∴ using equation
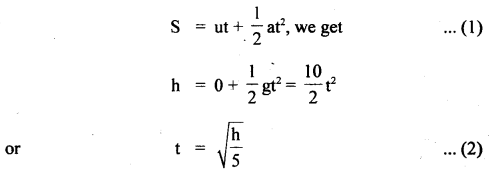
∴ t – 1 = Time taken by the second stone to reach the ground and
h – 20 = height of the point from where it is dropped l.
∴ u2 = initial velocity = 0
Thus using equation (1), we get
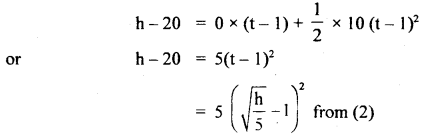

Question 5.
A body travels half of its total path in the last second of its fall from rest. Calculate the time and height of fall.
Answer:
Let h = height of fall
t = time of fall
a = g = 9.8ms-2
u = 0
∴ using equation,
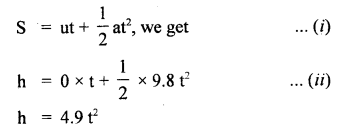
Also according to the statement first half i.e. \(\frac{h}{2}\) is covered in (t – 1)s.
∴ using (i), we get
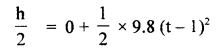

As last half of the journey takes 1 s, so t cannot be less than 1 s.
∴ t = 3.41s
∴ From(ii), h = 4.9 × (3.414)2
= 57.11 m
∴ h = 57.11, t = 3.414s.
Question 6.
A train moves from one station to another in 2h time. Its speed during the motion is shown in fig. Calculate
(a) the maximum acceleration during the journey.
(b) the distance covered during 0.75 to 1.00 h interval.
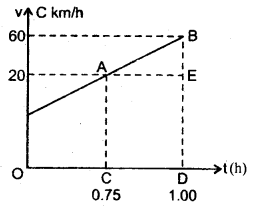
Answer:
(a) Maximum acceleration during the journey
= slope of AB part of the graph
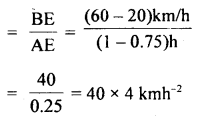
∴ acceleration = 160 kmh-2.
(b) Distance covered during the interval 0.75 to 1.00 h
= Area under the v -1 curve from 0.75 to 1.00
= Area of trapezium CABD
= Area of rectangle AEDC + area of AAEB

Question 7.
When the speed of the car is y, the minimum distance over which it can be stopped is z. If the speed of the car becomes v, then what will be the minimum distance over which it can be stopped?
Answer:
Case I:
Here, the initial velocity of car = v
The final velocity of car = 0
Let a = acceleration of car Distances covered before stopping = x
∴ Using the equation,
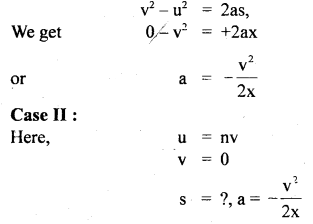
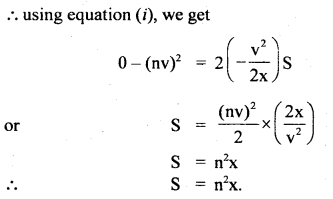
Question 8.
A body describes 10m in the third second and 12m in the Sth second with uniform acceleration. Find the distance covered by it in :
(a) next 3′ seconds and
(b) 8th second of its motion.
Answer:
Let the initial velocity of body = v
and let acceleration of body = a
Also, we know that distance covered during the nth second is given by
Snth =u + \(\frac{a}{2}\)(2n – 1)
∴ Distance travelled in 3rd and 5th second is:
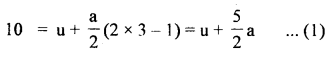
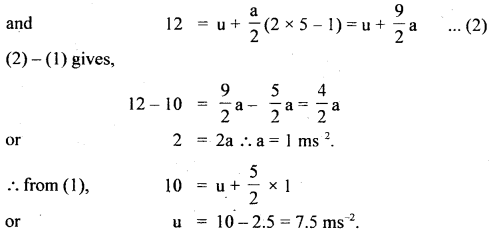
(a) using the equation, S = ut + at2, Let us find the distance covered by the body in 5s and 8 seconds.
Take u = 7.5,ms-1, a= I ms2
If x1 and x2 be the distances covered in 5s and 8s respectively.
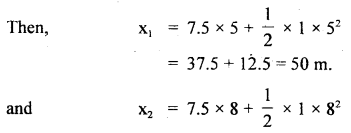
= 60 + 32 = 92 m
∴ Distance travelled by the body in next 3 seconds is given by
= x2 – x1
= 92 – 50 = 32 m
(b) The distance trave1ìdby the body in 8th second (x8) is given by
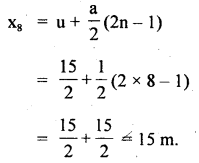
Question 9.
The velocity of an object (ms-1) moving along a straight line is given by
v = 10 + 3t2 …. (1)
Find (a) change in velocity in the interval when t = 2s and 5s.
(b) average acceleration in the same interval.
(c) instantaneous acceleration at t = 4s.
Answer:
Comparing equation (1), with the equation v = u + at, we find that u = 10ms-1,
(a) Now velocity of the object after 2 and 5 seconds is calculated as :
v = 10 + 3t2
putting t = 2, v = 10 + 3 × 22 = 10 + 3 × 4 = 22ms-1
putting t = 5, v = 10 + 3 × 52 = 10 + 3 × 25 = 85 ms-1.
∴ Change in velocity from 2s to 5 s
= 85 – 22 = 63 ms-1.
(b) We know that average acceleration in a given time interval is given by
aav = \(\frac{\Delta \mathrm{v}}{\Delta \mathrm{t}}\)
Thus aav in the interval 2s to 5 is given by
aav = \(\frac{85-22}{5-2}=\frac{63}{3}\) = 21 ms-2.
(c) We know that instantaneous acceleration is given by
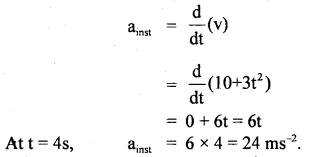
Question 10.
A car travels at a rate of 30 km h-1 for 5 minutes and then at 40 km h-1 for 10 minutes.
Find (i) the total distance covered by the car
(ii) the average speed of the car.
Answer:
v1 = 30 kmh-1 t1 = 5 min = \(\frac{5}{60}\) h = \(\frac{1}{12}\) h.
If S1 be the distance covered in 5 min., then
S1 = v1 t1 = 30 × \(\frac{1}{12}\) = \(\frac{5}{2}\) km = 2.5 km
Now v2 = 40 kmh-1, t2 = 10 minutes = \(\frac{1}{6}\) h
If S2 = distance covered in 10 min., then
S2 = v2 t2 = 40 × \(\frac{1}{6}\) = \(\frac{20}{3}\) km = 6.67 km.
(i) If S be the total distance, then
S = S1 + S2 = 2.5+ 6.67 = 9.17 km.
(ii) If vav be the average speed of the car,

Question 11.
A particle covered half the distance with a velocity v0. The remaining half distance was covered with a velocity v1 for half the time and with velocity v2 for another half of the time. Find the mean speed of the particle averaged over the whole time of motion.
Answer:
Let S = total distance covered by the particle.
t1 = time taken to cover half the distance i.e. \(\frac{S}{2}\)
v0 = velocity of the particle
\(\frac{S}{2}\) = Distance covered with v0.
∴ using equation x = ut, we get
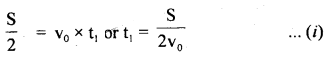
Now let 2t = time to cover the remaining distance \(\frac{S}{2}\).
If S1 = distance covered with v1 in time t.
S2 = distance covered with v2 in time t,
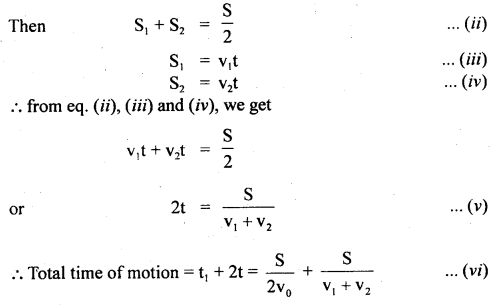

Question 12.
In a circus, a motorcyclist takes 4 rounds on the same track in the globe of radius r with a velocity 5r.
Find (i) total displacement
Answer:
radius of track = r, velocity v = 5r.
As the starting and endpoint in a circular track are the same, so the net displacement = 0
(ii) total distance covered
Answer:
Distance covered in one round = perimeter of the circular track of radius r
= 2π x r
∴ total distance covered in 4 rounds = 4 × 2πr = 8πr.
(iii) total time is taken by him.
Answer:
Let t = time taken by the motorcyclist in completing 4 rounds.

Question 13.
The displacement of a particle moving in one dimension under the action of a constant force is related to the time t by the equation t = \(\sqrt{x}\) + 3, where x is in metre and t is in second. Find the displacement of the particle when its velocity is zero.
Answer:
t = \(\sqrt{x}\) + 3
\(\sqrt{x}\) = t – 3 ….(1)
Squaring on both sides of equation (1), we get
x = (t – 3)2
= t2 + 9 – 6t …..(2)
If v be the velocity of the particle,
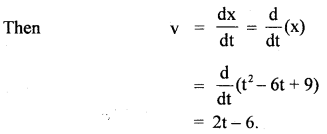
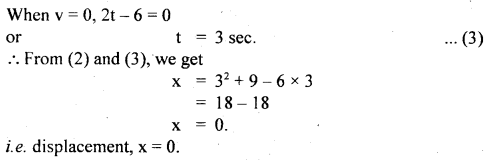
Question 14.
A car moving along a straight road with a speed of 144 km h-1 is brought to a stop within a distance of 200 m. Calculate its retardation and the time it takes to stop.
Answer:
Here, S = distance covered before topping = 200 m.
u = initial speed of car = 144 km h-1 = 144 × \(\frac{5}{18}\) ms-1 = 40 ms-1
v = its final speed = 0
Let a = retardation of the car =?
using the relation,
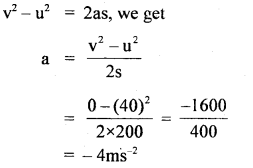
Also Let t = time taken ?
∴ using the relation, v = u + at, we get
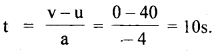
Question 15.
A stone falls from the top of the tower in 8s. How much time will it take to cover the first quarter of the distance starting from the top?
Answer:
Here u = initial speed oftcie = 0
h = height of tower
t = time taken in falling by h = 8s
Let t1 = time taken to cover first quarter i.e. \(\frac{h}{4}\) = ?
a = g = acce. due to gravity
using the relation, S = ut + \(\frac{1}{2}\)at2
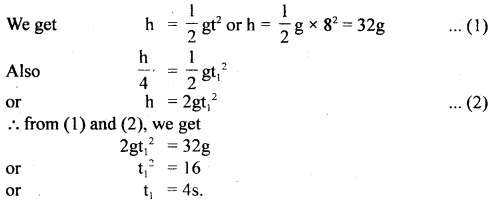
Question 16.
A ball is thrown vertically upwards with a velocity of 30 ms-1. If access. due to gravity is 10 ms-2, what will be the distance travelled by ¡tin the first and last second of upward motion?
Answer:
Here, u = initial velocity in the upward direction 30ms-1
Let after a time t, the ball stops i.e. v = 0
a = acce.= g = 10 ms-2
Let Snth be the distance covered by the ball in the last second i.e. nth second of its motion =7
∴ using the relation, v = u + at,

Let x1 be the distance covered by it in first second of its motion,
∴ using the relation, S = ut + \(\frac{1}{2}\) gt2, we get
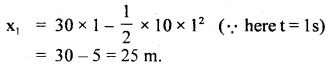
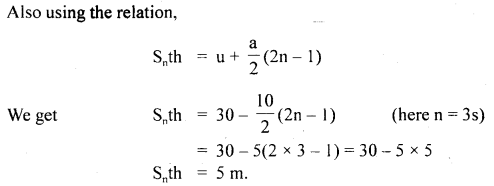
Question 17.
A rocket is fired vertically from the ground. It moves upwards with a constant acceleration of 10 ms-2 for the 30s after which the fuel is consumed. After what time from the instant of firing, the rocket will attain the maximum height? Take g = 10ms-2.
Answer:
Here, a = g = 10ms-2 for t = 30s
∴ u = 0 for first part of the motion
v = velocity attained by the rocket after 30s = ?
∴ using the relation,
v = u + at …(1)
we get v = 0 + 10 × 30
= 300 ms-1
for second part of motion,
u = v = 300 ms-1
v1 = final velocity = 0
Let t1 be the time of journey for this part of the motion,
∴ from equation (1), we get
0 = 300 – 10 × t1
Let T = total time of flight in which the rocket attains maximum height,
T = t + t1
= 30 + 30
= 60 second.
Question 18.
On a foggy day, two car drivers spot each other when they are just 80 m apart. They were travelling at 72 km h-1 and 60 km h-1 respectively. Both of them simultaneously apply brakes which retard both the cars at 5ms-2. Tell whether they will avert a collision or not?
Answer:
Here, let u, and u2 be the initial velocities of the two cars.

If S1 and S2 be the distances covered by the two cars before coming to rest (i.e. v = 0), then
using the relation,
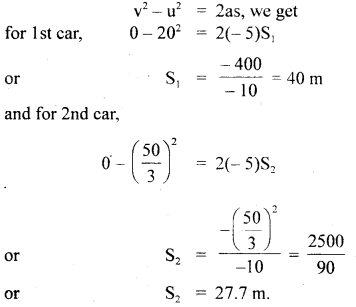
If S be the total distance covered by two cars before coming to rest, then
S = S1 + S2 = 40 + 27.7 = 67.7 m.
Also S1 = 80 m.
Now clearly the total distance covered by the cars before coming to rest is less than 80 m, so the collision will be averted.
Question 19.
A stone is dropped from a rising balloon at a height of 76 m above the ground and reaches the ground in 6s. What was the velocity of the balloon when the stone was dropped?
Answer:
Let u be the velocity of the balloon in an upward direction at the point
A = initial velocity of stone in an upward direction.
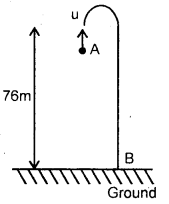
The stone rises to the top, comes to rest and then it starts coming back to the ground to hit B.
Let us take A as origin :
∴ Net vertical distance covered by the stone, y = – 76 m.
a = – g = – 9.8 ms-2
(Here y and acc. are taken as -ve because they are in a downward direction w.r.t. A)
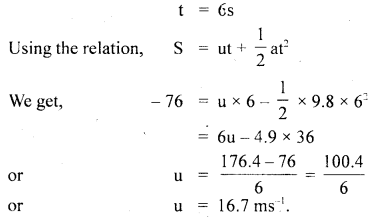
Question 20.
A car moves at a velocity of 2.24 km h-1 in the first minute, at 3.60 km h-1 in the second minute and at 5.18 km h-1 in the third minute. Calculate the average velocity in these three minutes.
Answer:
Let x1, x2 and x3 be the displacements of car in 1 st, 2nd and 3rd minutes respectively and let v1, v2 and v3 be the velocities of these time intervals,
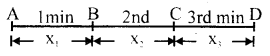
∴ v1 = 2.24 kmh-1, v2 = 3.60 kmh-1, v3 = 5.18 kmh-1
time intervals = t1 = t2 = t3 = 1 minute = \(\frac{1}{60}\) h
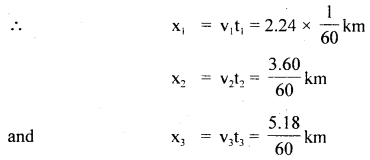
If x be the total displacement, then
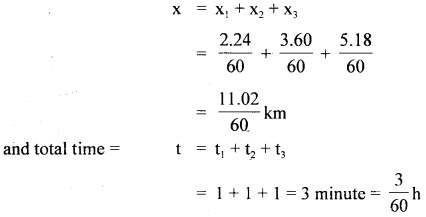
If v be the average velocity in these 3 minutes, then

Question 21.
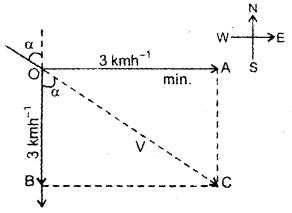
A man is walking due East at the rate of 3 km h-1. Rain appears to fall down vertically at the rate of 3 km h-1. Find the actual velocity and direction of the rainfall.
Answer:
Let a = angle made by the rainfall with the vertical Velocity of man represented by OA due East = 3 km h-1
As rain appears to fall vertically downward, so OB = 3 km h-1 represents the velocity of rain w.r.t. man. The actual velocity of rainfall is represented by OC and is given by

Thus the rain is actually falling at 3\(\sqrt{2}\) km h-1 at an angle of 45° west of the vertical.
Question 22.
A car starting from rest and moving with uniform acceleration possesses average velocities 5 ms-1, 10 ms-1 and 15 ms-1 in the first, second and third seconds. What is the total r distance covered by the car in these three seconds?
Answer:
Here, let v1, v2 and v3 be the average velocities of 1st, 2nd and 3rd secs, respectively.
∴ v1 = 5 ms-1, v2 = 10 ms-1, v3 = 15 ms-1
t1 = t2 = t3 = 1 s = time intervals
If x1, x2 and x3 be the distances covered in these seconds resp., then
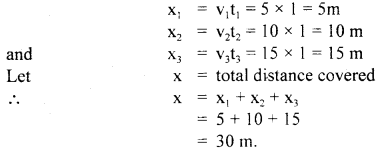
Question 23.
A person is running at a maximum speed of 3 ms-1 along the length of a train to catch hold of the door of a compartment. When he is just 2.5 m from the door, the train steams off with an acceleration of 1 ms-2. Find how long it takes him to catch the door?
Answer:
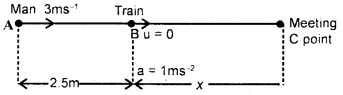
Here, let u1 = 3 m s-1, be the initial speed of man at point A.
For train x1 = 2.5 m = distance of the train from man.
u = 0, a = acceleration of train = 1 ms-2
Let C be their meeting point after a time t.
If BC = x, then usirig the relation,
S = ut + \(\frac{1}{2}\) at2, we get
For train, x = 0 + \(\frac{1}{2}\) × 1 × t2 = 0.5t2 … (1)
For man, using the relation,
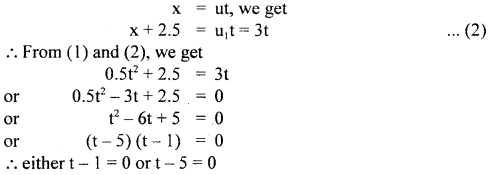
∴ t = 1, 5 i.e. he will catch the door first after Is and then after 5s.
t = 1s.
Question 24.
The displacement of a body along the x-axis changes according to the relation: x = 20 – 15t + 4t2, where x is in metres, t in seconds. Determine its position, velocity and acceleration at t = O.
Answer:
Here, x = 4t2 – 1 5t + 20 … (1)
v = \(\frac{\mathrm{d} \mathrm{x}}{\mathrm{dt}}\) = 4.2t – 15 = 8t – 15 …(2)
Also a = \(\frac{\mathrm{d} \mathrm{v}}{\mathrm{dt}}\) = 8
At t = 0, the position (x), velocity (y) and acceleration (a) are given by
x = 4.0 – 15 × 0 + 20 = 20 m
v = 8 × 0 – 15 = – 15ms-1
and a = 8 ms-2.
Question 25.
A body undergoes a uniformly accelerated motion. Its velocity after 5 seconds is 25 ems and after 8 seconds it is 34 cms’. Calculate the distance covered in the 12th second.
Answer:
Let u and a be the initial speed and acceleration of the body.
Let v1 and v2 be its velocities after 5s and 8s respectively

Let Snth be the distance covered in the 12th second.
Using the relation,
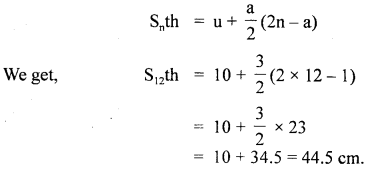
Value-Based Type:
Question 1.
On a two-lane road, there are hoardings hanged on the electric poles “Save Energy”.
If car a is travelling at a speed of 54 km h1 and car ‘B’ moves with 90 km h-1 from the opposite direction.
Now, answer these questions:
(a) Which values are depicted in the above problem? Write down the four ways by which the energy can be saved.
Answer:
Save energy to save our environment.
The four ways to save energy are as under :
- By using CFLs, switching off appliances when not in use.
- Saving water by using it efficiently.
- Using solar energy.
- By using public transport.
(b) Write a slogan on “save energy”.
Answer:
Try your self
(c) Find the velocity of B with respect to A? Also, find the velocity of the ground with respect to B?
Solution:
VA = + 54 km h-1 = 15 ms-1
VB = 90 km h-1 = – 25 ms-1
(Takingthe velocity of car A positive N v and car B negative)
∴ Relative velocity of B with respect to A
= VB – VA = – 25 – 15 = – 40 ms-1
i.e the car Bappers to A to move with a speed 40 ms-1 from opposite direction.
Relative velocity of ground w.r.t B = 0 – VB = 0 – (- 25)
= 25 ms-1
Question 2.
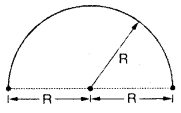
A candle march was organised by an NGO. The theme of the candle march was “No use of non-biodegradable products”. The organizer made a semicircular track of radius R on which peoples have to run taking a poster in their hands. If Mahesh travelled from A to B in time t with constant speed, then answer the following:
(i) Why should non-biodegradable products not be used? Justify your answer.
Answer:
Biodegradable products are reusable and cause less pollution. So, non-biodegradable products must be avoided.
(ii) Find the
(a) Displacement
Answer:
Displacement = minimum distance between initial and final point = AB = 2 R
(b) Average speed
Answer:
![]()
(c) Average velocity
Answer:
![]()
(d) Average acceleration
Answer:
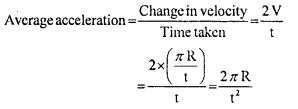
Question 3.
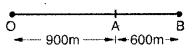
In sports day activities of a public school, the lines were drawn with chalk powder. Gagandcep an athlete runs a distance of 1500 m in the following manner, (i) Starting from rest, he accelerates himself uniformly at 2ms_1, till he covers a distance of 900 m. (ii) He then runs the remaining distance of 600 m at the uniform speed developed.
(i) Which value is depicted in the above problem?
Answer:
Importance of sports activities.
(ii) Do you think that sports activities are important in day-to-day life?
Answer:
Yes, sports activities are very much important in day-to-day life as
(a) It gives break from regular life
(b) It improves physical strength
(c) It relaxes our mind and body
(d) It helps to concentrate on other works
 im-90
im-90
(iii) Calculate the time taken by the athlete to cover the two parts of the distance covered.
Answer:
Let the athlete run from O to B Here, OB = 1500 m,
OA = 900 m, AB = 600 m
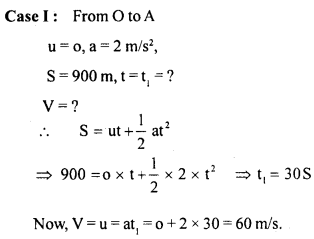
Case II : Taking motion of athelete from A to B u = 60 m/s, S = 600m, a = o (∵ Speed is uniform or constant)
t = t2 = ?
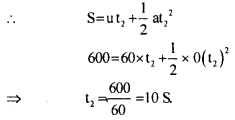
Question 4.
An old woman crossing the road was holding a money purse. She was not able to walk. A pickpocket snatches away her purse. A school student of class XI having seen this incident tries to help that old lady. He informs the polic^inspector who stands nearby. The inspector collects the money purse from the pickpocket and hands it over to the old lady.
(a) What value do you find in the school student?
Answer:
The student is sympathetic towards others, helping, and applies his presence of mind in solving the problems, knows how to use public services.
(b) Also the police inspector in a jeep is chasing the pickpocket on a straight road. The jeep is going at its maximum speed ‘v’. The pickpocket rides on the motorcycle of a waiting friend when the jeep is at a distance ‘d’ away. And the motorcycle starts with a constant acceleration ‘a’. Show that the pickpocket will be caught if v ≥ \(\sqrt{2ad}\).
Answer:
Let the police inspector catches the pickpocket after time t.
The distance covered by the pickpocket in this time interval is given by:
s = \(\frac{1}{2}\) at2
Distance travelled by the inspector (s1) = vt
the police inspector will catch the pickpocket if
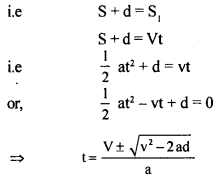
The police inspector will catch the bus if t is real i.e v2 ≥ 2ad or v ≥ \(\sqrt{2ad}\)
Hence, the minimum speed of the police inspector for catching the pickpocket is \(\sqrt{2ad}\) proved.