Work, Energy and Power Class 11 Important Extra Questions Physics Chapter 6

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 6 Work, Energy and Power. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 6 Important Extra Questions Work, Energy and Power

Work, Energy and Power Important Extra Questions Very Short Answer Type

Question 1.
What is the source of the kinetic energy of the falling raindrops?
Answer:
It is the gravitational potential energy that is converted into kinetic energy.

Question 2.
A spring is stretched. Is the work done by the stretching force positive or negative?
Answer:
Positive because the force and the displacement are in the same direction.

Question 3.
What is the type of collision when?
(a) Does a negatively charged body collide with a positively charged body?
Answer:
Perfectlyjnelastic collision.

(b) Do macroscopic bodies collide?
Answer:
Inelastic collision.

(c) Do two quartz balls collide?
Answer:
Perfectly elastic collision.

Question 4.
(a) Give two examples of potential energy other than gravitational potential energy.
Answer:
Electrostatic P.E. and elastic P.E.

(b) Give an example of a device that converts chemical energy into electrical energy.
Answer:
Daniell cell.

(c) Heat energy is converted into which type of energy in a steam engine?
Answer:
Mechanical energy.

(d) Where is the speed of the swinging pendulum maximum?
Answer:
At the bottom of the swing.

(e) A heavy stone is lowered to the ground. Is the work done by the applied force positive or negative?
Answer:
Negative work.

Question 5.
What is the work done by the centripetal force? Why?
Answer:
Zero. This is because the centripetal is always perpendicular to the displacement.

Question 6.
(a) What is the work done by the tension in the string of simple pendulum?
Answer:
zero

(b) What is the work done by a porter against the force of gravity when he is carrying a load on his hand and walking on a horizontal platform?
Answer:
zero

(c) Name the force against which the porter in part (A) is doing some work.
Answer:
Frictional force.

Question 7.
When an arrow is shot, wherefrom the arrow will acquire its K.E.?
Answer:
It is the potential energy of the bent bow which is converted into K.E.

Question 8.
When is the exchange of energy maximum during an elastic collision?
Answer:
When two colliding bodies are of the same mass, there will be a maximum exchange of energy.

Question 9.
Does the work done in raising a load onto a platform depend upon how fast it is raised?
Answer:
The work done is independent of time.

Question 10.
Name the parameter which is a measure of the degree of elasticity of a body.
Answer:
Coefficient of restitution.

Question 11.
When a ball is thrown up, the magnitude of its momentum first decreases and then increases. Does this violate the conservation of momentum principle?
Answer:
No. This is because the momentum of the system (ball and air molecules) remains constant. When the momentum of the ball decreases, the momentum of air molecules in contact increases and vice-versa.

Question 12.
In a tug of war, one team is slowly giving way to the other. What work is being done and by whom?
Answer:
+ve. The winning team is performing work over the losing team.

Question 13.
A light and a heavy body have equal momentum. Which one of them has more K.E.?
Answer:
The lighter body has more K.E.

Question 14.
By using simple mechanical devices such as a lever, wedge, inclined plane, pulley, wheel, etc. we can do work even by applying small force. What makes it possible to do so?
Answer:
These mechanical devices multiply forces.

Question 15.
Two protons are brought closer. What is the effect on the potential energy of the system?
Answer:
Work is done to overcome the force of repulsion, so the potential energy of the system increases.

Question 16.
Where is the energy of a vertically projected body maximum?
Answer:
It is the same at all points. This is in accordance with the law of conservation of energy.

Question 17.
Out of a pair of identical springs of force constants, 240Nm^-1 one is compressed by 10 cm and the other is stretched by 10 cm. What is the difference in the potential energies stored in the two springs?
Answer:
The difference in potential energies is zero. This is because
E_p = \(\frac{1}{2}\) ky². In both cases, k and y² are the same.

Question 18.
What should be the angle between the force and the displacement for maximum and minimum work?
Answer:
For maximum work, θ = 0° and for minimum work θ = 90°.

Question 19.
Does the P.E. of a spring decreases/increase when it is compressed or stretched? Why?
Answer:
P.E. of a spring increases in both cases. This is because work is done by us in compression as well as in stretching the spring.

Question 20.
Can a body have momentum without energy?
Answer:
No, because for momentum, it must have some velocity and hence energy.

Question 21.
What type of energy is stored in the spring of the watch?
Answer:
Potential energy.

Question 22.
Can a body have energy without momentum?
Answer:
Yes, everybody has some internal energy due to the thermal agitation of the particles of the body. But the vector sum of linear momenta of the moving particles may be zero. It may have energy due to its position (P.E.) and thus momentum is zero.

Question 23.
In which motion, momentum changes but not the K.E.?
Answer:
In uniform circular motion.

Question 24.
Is the whole of K.E. lost in any perfectly inelastic collision?
Answer:
No, only as much K.E. is lost as is necessary for the conservation of linear momentum.

Question 25.
Can the P.E. of an object be negative?
Answer:
Yes, it can be negative when the forces involved are attractive.

Question 26.
The momentum of a body is increased by 50%. What is the percentage change in its K.E.?
Answer:
When the momentum is increased by 50%, velocity increases by
i.e. velocity becomes \(\frac{3}{2}\) times, so K.E. becomes \(\frac{9}{4}\) times
i.e. \(\frac{9}{4}\) × 100 = 225%. Hence increase in K.E. = 225 – 100 = 125%.

Question 27.
What is the work done by Earth’s gravitational force in keeping the moon in its orbit in a complete revolution?
Answer:
Zero, because gravitational force is a conservative force.

Question 28.
A spring is cut into two equal halves. How is the spring constant of each half affected?
Answer:
The Spring constant of each half becomes twice the spring constant of the original spring.

Question 29.
What happens to the energy of our watch which we wind once a day?
Answer:
The work done in winding the watch is stored as P.E. in the spring which is converted into K.E. of the moving parts of the watch.

Question 30.
Is collision possible even without actual contact of the colliding particles? Give example.
Answer:
Yes, such collision is called collision at a distance. The collision between subatomic particles (like proton and neutrons) are examples of such collisions.

Question 31.
A cake of mud is thrown on a wall where it sticks. What happens to its initial K.E.?
Answer:
A part of the K.E. is used in deforming the cake and the remaining part is converted into heat and sound energy.

Question 32.
Nuclear fission and .fusion reactions are the examples of conversion of mass into energy. Can we say that strictly speaking, mass is converted into energy even in an exothermic chemical reaction?
Answer:
Yes, mass is converted into energy in an exothermic chemical reaction also. But the mass change in a chemical reaction is about a million times less than in a nuclear reaction.

Question 33.
What type of energy is lost in doing work against friction?
Answer:
The kinetic energy is lost in doing work against the friction.

Question 34.
Define 1 Joule.
Answer:
A joule of work is said to be done when a force of 1 N displaces a body through 1 m.

Question 35.
Define an erg.
Answer:
An erg of work is equal to work done by a force of 1 dyne of displacing a body through one centimeter.

Question 36.
Derive the relation between 1 J and 1 erg.
Answer:
We know that 1 J = 1 N × 1 m = 1 Nm

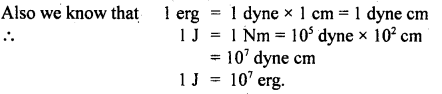
Question 37.
What is the nature of the work done by the resistive force of air on a vibrating pendulum in bringing it to rest and why?
Answer:
Negative, because the air always opposes the displacement of the pendulum bob.

Question 38.
What is the work done on a body in moving it in a circular path with a constant speed? Why?
Answer:
Zero, because it is acted upon by centripetal force in a direction perpendicular to its motion.
i.e. W = FS cos 90° = 0.

Question 39.
A truck and car are moving with the same K.E. and are brought to rest by the application of brakes that provide equal retarding force. Which one will come to rest in a shorter distance? Why?
Answer:
Both of them come to rest at the same distance as
K.E. = F.S₁ = F.S₂
or
FS₁ cos 180 = F.S₂ cos 180
or
S₁ = S₂.

Question 40.
A conservative force does positive work on a body. What happens to the potential energy of the body? Give an example.
Answer:
It (P.E.) decreases.
e.g. a body falling freely under gravity.

Question 41.
A man rowing a boat upstream is at rest w.r.t. the shore. Is any work being done in this case? Why?
Answer:
Yes, as there is a relative displacement between the boat and the stream.

Question 42.
Why friction is a non-conservative force?
Answer:
It is because the work done against friction along a closed path is non-zero.

Question 43.
Does the work done in raising a load onto a platform depend upon how fast it is raised?
Answer:
No, work done does not depend upon the time taken in doing it.

Question 44.
On what factors, does the work done depend?
Answer:
It depends upon the applied force and the displacement of the body.

Question 45.
How will the kinetic energy of a body change if its momentum is tripled? Why?
Answer:
K.E. becomes nine (9) times its initial value as K.E. ∝ p².

Question 46.
Which physical quantity is conserved during both the elastic and inelastic collision?
Answer:
Linear momentum is conserved in both collisions.

Question 47.
What is the most common feature of all types of collisions?
Answer:
Linear momentum is conserved in all types of collisions.

Question 48.
Define variable force.
Answer:
It is defined as the force which either changes in magnitude or direction.

Question 49.
Give an example of variable force.
Answer:
When an object is falling towards the Earth, the gravitational force acting on it goes on changing, so it is a variable force.

Question 50.
Define an electron volt (eV).
Answer:
It is defined as the K.E. acquired by an electron when a potential difference of 1 volt is applied across it.

Work, Energy and Power Important Extra Questions Short Answer Type

Question 1.
An airplane’s velocity is doubled,
(a) What happens to its momentum? Is the law of conservation of momentum obeyed?
Answer:
The momentum of the airplane will be doubled. Yes, the law of conservation of momentum will also be obeyed
because the increase in momentum of the airplane is simultaneously accompanied by an increase in momentum of exhaust gases.

(b) What happens to its kinetic energy? Is the law of conservation of energy obeyed?
Answer:
K.E. becomes four times. Yes, the law of conservation of energy is obeyed with the increase in K.E. coming from the chemical energy of fuel i. e. from the burning of its fuel.

Question 2.
In a thermal station, coal is used for the generation of electricity. Mention how energy changes from one form to the other. before it is transformed into electrical energy?
Answer:
When coal is burnt, heat energy is produced which converts water into steam. This steam rotates the turbine and thus heat energy is converted into mechanical energy of rotation. The generator converts this mechanical energy into electrical energy.

Question 3.
Chemical, gravitational and nuclear energies are nothing but potential energies for different types of forces in nature. Explain this statement clearly with examples.
Answer:
A system of particles has potential energy when these particles are held a certain distance apart against some force. For example, chemical energy is due to the chemical bonding between the atoms. Gravitational energy arises when the objects are held at some distance against the gravitational attraction.

Nuclear energy arises due to the nuclear force acting between the nuclear particles.

Question 4.
What went wrong at the Soviet atomic power station at Chernobyl?
Answer:
In this reactor, graphite was used as a moderator. The fuel elements were cooled by water and steam was produced from within the reactor. Both water and the steam came in contact with hot graphite. Due to this hydrogen and carbon-monoxide (CO) were released. When they came in contact with air, there was a big explosion.

Question 5.
A man can jump higher on the moon than on Earth. With the same effort can a runner improve his timing for a 100 m race on the moon as compared to that on Earth?
Answer:
Man can jump higher on the moon because the acceleration due to gravity on the moon is less than that on the Earth. But acceleration due to gravity does not affect the horizontal motion. Hence the runner can’t improve his timing on the moon for the 100 m race.

Question 6.
How many MeV are there in a 1-watt hour?
Answer:
We know that 1 watt hour = 1 JS^-1 × 3600 s = 3600 J

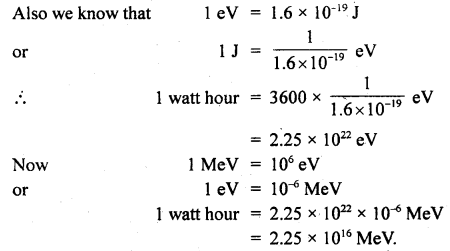
Question 7.
What is Newton’s experimental law of impact?
Answer:
The ratio of the relative speed of separation after a collision to the relative speed of approach before the collision is always constant. This constant is known as the coefficient of restitution. It is denoted by e.
∴ e = \(\frac{\mathbf{V}_{2 \mathrm{f}}-\mathbf{v}_{1 \mathrm{f}}}{\mathbf{u}_{1 \mathrm{i}}-\mathbf{u}_{2 \mathrm{i}}}\)

where u_1i and u_2i, are the velocities of the bodies before collision and v_2f, v_1f are the velocities of the bodies after the collision.

Question 8.
Two masses one n times as heavy as the other have the same K.E. What is the ratio of their momenta?
Answer:

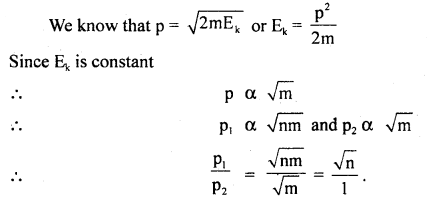
Question 9.
Two bodies A and B having masses m_A and m_B respectively have equal K.E. If p_A and p_B be their respective momenta, then prove that the ratio of momenta is equal to the square root of the ratio of respective masses. f_c.
Answer:
Let v_A and v_B be the velocities of A and B respectively.
Since their kinetic energies are equal,


Hence Proved

Question 10.
How fast-moving neutrons can be quickly slowed down by passing through heavy water?
Answer:
Heavy water (D₂O) contains deuterium atoms i.e. hydrogen nuclei. They have nearly the same mass as those of neutrons. So when neutrons strike against deuterium atoms, most of the K.E. of the former is transferred to the deuterium atoms i.e. K.E. is exchanged between them.

Question 11.
Will water at the foot of the waterfall be at a different temperature from that at the top? If yes, explain.
Answer:
Yes, when water reaches the ground, its gravitational potential energy is converted into kinetic energy which is further converted into heat energy. This raises the temperature of the water. So water at the foot of the waterfall is at a higher temperature as compared to the temperature of water at the top of the waterfall.

Question 12.
How is the kinetic energy of a particle related to the direction of motion of the particle? Can K.E. be negative?
Answer:
The kinetic energy of a particle is not related to the direction of motion of the particle. K.E. is always positive. It cannot be negative.

Question 13.
An automobile jack is employed to lift a heavyweight. The applied force is much smaller than the weight of the automobile. Can it be said that the work is done in less than the work done in? lifting the automobile directly through a height.
Answer:
No, in the case of the automobile jack, the work done is not calculated from the equation W = FS cos θ, but the work done is calculated from an equation (W = τ θ = FRθ) of rotational motion. In both cases, the same amount of work is done.

Question 14.
What would be the effect on the potential energy of the system of two electrons brought closer?
Answer:
Work has to be done to overcome the force of repulsion. This work done will be stored in the form of P.E. so, it increases the potential energy of the system.

Question 15.
Can the kinetic energy be increased without the application of an external force? If yes, give an example.
Answer:
Yes, this is possible. If work is done by the internal force, then K.E. will be increased. As an example, when a bomb explodes, the combined K.E. of all the fragments is greater than the initial K.E.

Question 16.
Mountain roads rarely go straight up the slope, but wind up gradually why?
Answer:
If roads were to go straight up, the slope (θ) would have been large, the frictional force (µmg cos θ) would be small. The wheels of the vehicle would slip. Also for going up a large slope, a greater power shall be required.

Question 17.
A truck and a car moving with the same K.E. are stopped by applying the same retarding force by means of brakes. Which one will stop at a smaller distance?
Answer:
Both will stop at the same distance which follows from the work-energy theorem.
K.E. = work done in stopping= retarding force × distance
As K.E. and force for both are equal, so the distance covered must be equal.

Question 18.
A truck and a car are moving with the same K.E. on a straight road. Their engines are simultaneously switched off. Which one will stop at a lesser distance?
Answer:
The vehicle stops when its K.E. is spent working against the force of friction between the tires and the road. This force of friction varies directly with the weight of the vehicle.

As K.E. = work done
= force of friction × distance
or
E = F × S
or
S = E/F.
Forgiven K.E., S, will be smaller where F is larger such as in the; case of a truck.

Question 19.
A man rowing a boat upstream is at rest w.r.t. the shore. Is any work being done in this case?
Answer:
No, because the man is applying the force and there is no relative motion between the boat and the shore.

Question 20.
A body is heated by giving Q an amount of heat energy. Will its mass increase or decrease or remain constant? If it increases or decreases, then by how much?
Answer:
The variation in mass depends on the nature of the body. For most solids, there is no variation in mass on heating. However, if the solid is volatile, heating will change the mass of the solid. Heating of solids, in general, bring about a change in state, and during this process, some loss of mass occurs due to evaporation.

Question 21.
A football kicked by a player leaves the ground and after traveling in the air reaches the ground and comes to stop at some other position on the ground. Identify the energy transformation in this process. Is the energy of the ball conserved?
Answer:
The kinetic energy imparted to the ball is converted into potential energy at the highest point and a small part remains kinetic. Then it is converted into kinetic energy when it hits the ground. This energy is used up in overcoming the friction against air and the ground. Due to the dissipation of energy in overcoming friction against air and ground, the kinetic energy of the ball is not conserved.

Question 22.
A child enjoys going high and high in a swing by pumping energy. Explain the large amplitude from the rest position using the work-energy idea.
Answer:
The child pumps energy to the swing at the appropriate time and place from his muscular work. In each swing friction at hinges and air, friction reduces the velocity which he compensates by providing energy to the swing at the appropriate time which partly increases the amplitude of the swing as well. So, periodic muscular work provides the energy to the swing.

Question 23.
How fast neutrons can be slowed down by heavy water? Where does the energy go?
Answer:
The fast neutrons collide with water molecules and transfer a good part of their kinetic energy to the water molecules. As a result, the kinetic energy and hence the speed of the neutrons is decreased i.e. they are slowed down. The energy received by the water molecules increases their speed and there is an increase in the thermal energy of the mass of water.

Question 24.
Show that the work done by an elastic force on a spring is stored as the potential energy of the spring.
Answer:
Consider an elastic spring that is extended or compressed. The force does not remain constant in this case. The elastic force Fel according to Newton’s Third law of motion is
F_el = – F_ext
when F_ext = external force applied
The Fel is always proportional to the compression or extension
i.e. F_el = – kx
∴ F_ext = kx
If F_av be the average force, then

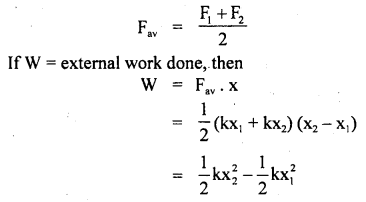
If x₁ = O (choosing x₁ as origin), then x₂ = x
The work done by an elastic force is stored as potential energy in the spring and is given by
W = P.E. = \(\frac{1}{2}\) kx².

Question 23.
What ¡s transformation of energy? Give at least five exam pies.
Answer:
The change of energy from one form to another is known as energy transformation. For example:

1. Diesel on burning produces hot gases and heat which is transformed into mechanical energy and is used to run trains and motor vehicles or pumps.
2. Electric energy is transformed into light in a tube or bulb.
3. The electric energy is changed into heat in an oven or heater.
4. Light is converted into electricity with the help of a photovoltaic cell.
5. In a microphone, sound energy is converted into electrical energy.

Question 26.
Which of the following does work: the hammer or the nail, a cricket bat or a ball? Explain.
Answer:
Hammer does work on nails. The force is applied by a hammer on the nail (object) and moves it through some distance. A bat does work on the ball and pushes. Initially, the bowler does work on the ball which init turn exerts impulse on the bat. The bat reacts with the added force of the batsman and thus, the bat does work on the ball.

Question 27.
A particle of mass m is moving in a horizontal circle of radius r under a centripetal force equal to \(\frac{\mathbf{k}}{\mathbf{r}^{2}}\) where k is a constant. What is the total energy of the particle?
Answer:

Question 28.
What are the relations between
(a) kilowatt hour and kilocalorie?
Answer:


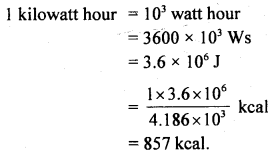
(b) metric horsepower and kilocalorie per hour?
Answer:

Question 29.
Prove that instantaneous power is given, by the dot product of force and velocity i.e. P = F.v.
Answer:
Let AW be the amount of work done in a small time interval Δt. If Pav be the average power, then

where F constant force producing a displacement S
∴ From (ii) and (iii), we get

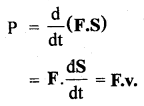
Question 30.
Define spring constant or force constant. What is its S.I. unit?
Answer:
It is defined as the extension per unit displacement produced in the spring or wire.
According to Hook’s law, the extension is always directly proportional to the tension or force applied on a spring i.e.
F ∝ x
or
F = k x
or
k = \(\frac{F}{x}\)

where k is the force constant
S.I unit of k is Newton metre^-1 (Nm^-1).

Work, Energy and Power Important Extra Questions Long Answer Type

Question 1.
(a) State work-energy theorem or principle.
Answer:
It states that the work done on a body is equal to the change in its kinetic energy.
i.e. W = change in kinetic energy
Proof: Let m = mass of a body moving in a straight line with a constant initial velocity u.

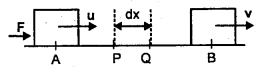
Let F = force applied on it at point A to B so that its velocity is V at B.
If dx = small displacement from P to Q
and a = acceleration produced in the body, then
F = ma

If dw be the work done from P to Q, then

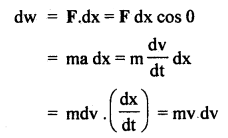
If W = total work done from A to B, then

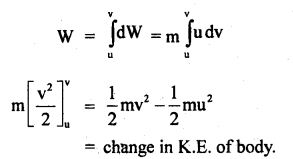
(b) State and prove the law of conservation of energy.
Answer:
It states that energy can neither be created nor can be destroyed but it can be changed from one form of energy into another i.e. total energy = constant.

Proof: Let a body of mass m be lying at rest at point A at a height h above the ground. Let it be allowed to fall freely and reaches a point B after falling through a distance x and it finally hits the ground at point C. Let v and V be its velocities at points B and C respectively.
∴ AB = x and BC = h – x

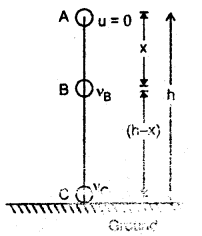
At point A: u = 0
∴ K.E. = 0
P.E. = mgh

If E be the total energy of the body, then
E = K.E. + P.E. = 0 + mgh
or
E = mgh …. (i)

At point B: using the relation,

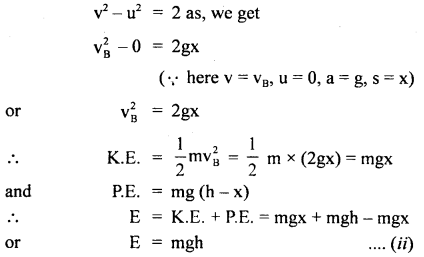
At point C: Here, v = v_c, a = g, s = h

Thus, from (i), (ii), and (iii), it is clear that total energy at points A, B, and C is the same. It is purely P.E. at A and purely K.E. at point C.

Numerical Problems:

Question 1.
An engine draws a train up an incline of 1 in 100 at the rate of 36 km h^-1. If the resistance due to friction is 5 kg wt per ton, calculate the power of the engine. Mass of train and engine is 100

Answer:
Here, m = 100 metric ton = 100 × 1000 kg
Total force of friction,
f1 = 100 × 5 = 500 kg wt
= 500 × 9.8 N = 4900 N
sin θ = \(\frac{1}{100}\)

Let f2 = Downward force on the train
= component of its weight acting in downward direction parallel to the inclined plane = mg sin θ
= 100 × 1000 × 9.8 × \(\frac{1}{100}\) = 9800 N

If F be the total force against which engine has to work, then

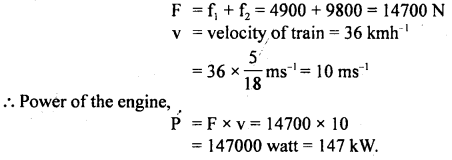
Question 2.
Calculate the work done and power of an engine that can maintain a speed of SO ms^-1 for a train of mass 3 × 106 kg on a rough level track for 5 km. The coefficient of friction is 0.05. Given g = 10 ms^-2.
Answer:
Here,

Question 3.
A 10 kg block slides without acceleration down a rough inclined plane making an angle of 20° with the horizontal. Calculate the work done over a distance of 1.2 m when the inclination of the plane is increased to 30°.
Answer:
Here, angle of sliding = 20°
μ = coefficient of friction
= tan 20° = 0.3647
S = 1.2 m

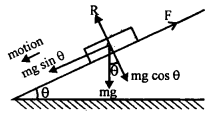
m = mass of block = 10 kg.

Let a = acceleration when the inclination is increased to 30° and F be the value of limiting friction then

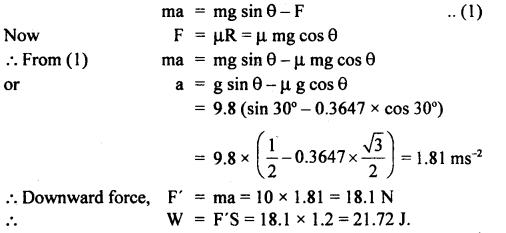
Question 4.
A bullet of mass 0.03 kg moving with a speed of 400 ms^-1 penetrates 12 cms into a fixed block of wood. Calculate the average force exerted by the wood on the bullet.
Answer:
Here,
mass of bullet, m = 0.03 kg
initial K.E. = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × 0.03 × (400)² = 2400 J
Final K.E. = \(\frac{1}{2}\)mv² = 0

∴ ΔK = Loss in kinetic energy = 2400 J
Let F = average force applied by block on bullet
S = 0.12 m

∴According to work energy principle
W = ΔK
or
FS = ΔK
or
F × 0.12 = 2400
or
F = 2 × 104 N

Question 5.
A boy of mass 50 kg sits in a swing suspended, by a rope 5 m long. A person pulls the swing to one side so that the rope makes an angle of 30° with the vertical. What is the gain in gravitational P.E. of the boy?
Answer:
Here, θ = 30°
OA = OB = 5 m …. (i)
m = 50 kg

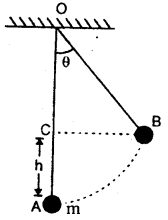
Vertical height through which boy at B rises up is given by

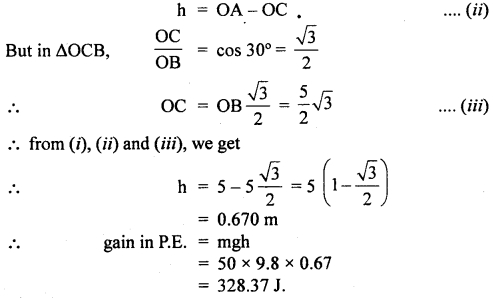
Question 6.
(a) bullet of mass 20 g moving with a velocity of 500 ms^-1 strikes a tree and goes out from the other end. with a velocity of 400 ms^-1. Calculate the work done in passing through the tree.
Answer:
Here m = 0.02 kg
u = 500 ms^-1
v = 400 ms^-1
w = ?
from work energy theorem, work done loss in K.E.

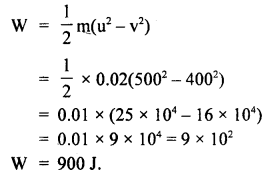
(b) A bullet of mass 0.01 kg is fired horizontally into a 4 kg wooden block at rest on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.25. The bullet remains embedded in the block and the combination moves 20 m before coming to rest. With what speed did the bullet strike the block?
Answer:
Here S = 20 m
μ = 0.25
M = mass of block = 4 kg
m = mass of bullet = 0.01 kg

∴ R = normal reaction = Mg = 4 × 9.8
F = μR = 0.25 × 4 × 9.8 = 9.8 N
v = 0
u = ?
or
loss in KE. = work done by the force of friction against the block.

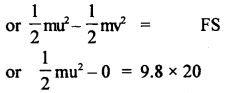
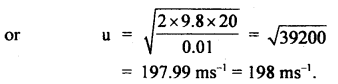
Question 7.
A stone of mass 5 kg falls from the top of a cliff 30 m high and buries itself one meter deep into the sand. Find the average resistance offered and time taken to penetrate into the sand.
Answer:
Here, m = 5 kg
h = 30 m
S = 1 m
∴ P.E. of stone = mgh = 5 × 9.8 × 30 = 1470 J

Let F = average force of resistance offered by the sand and F’ = net upward force.

Now momentum of stone before penetration
mu = mv = 5 × 24.25 (∵ here u = v)

Final momentum of stone when it becomes stationary (i.e. v’ = 0)
= mv’ = m(0) = 0
∴ Ft = – mv’ + mu

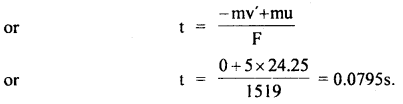
Question 8.
An automobile moving at a speed of 72 km h^-1 reaches the foot of a smooth incline when the engine is switched off. How much distance does the automobile go up the incline before coming to rest? Take angle of incline 30°, g = 9.8 ms^-2.
Answer:
Here, θ = 30°
Initial velocity of the automobile at point A when it is switched off = 72 kmh^-1
= 72 × \(\frac{5}{18}\) = 20 ms^-1

Let m = mass of automobile.
Initial K.E. of the automobile at A = \(\frac{1}{2}\) m(20)² = 200 m

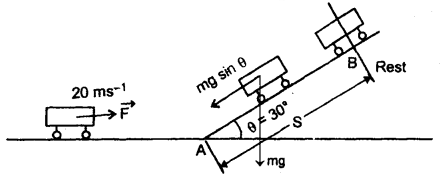
F = mg sin θ = force opposing the motion of the automobile
= m × 9.8 sin 30° = (4.9m)N

Let it stop at B after travelling AB = S
∴ Final K.E. = 0
∴ change in K.E. = 200m – 0 = 200m J
∴ W = work done by the automobile
= FS = (mg sin θ) × S = 4.9 m × S

∴ According to work-energy theorem,
W = change in K.E.
or
4.9m S = 200m
or
S = \(\frac{200}{4.9}\) = 40.8m

Question 9.
A pump-set is used to lift water to a reservoir of 6000 liters capacity over an average height of 20m. If it takes 1 hour to All the reservoir completely, calculate the work done and the power supplied to the set if its efficiency is 60%, g = 9.8 ms^-2.
Answer:
Mass of 1 litre of water = 1 kg .
∴ m = 6000 kg
h = 20 m

∴ W = work done = P.E. = mgh
= 6000 × 9.8 × 20= 11.76 × 10s J
t = 1 h = 3600 s

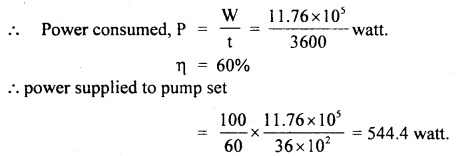
Question 10.
A wooden ball is dropped from a height of 2 m. What is the height up to which the ball will rebound if the coefficient of restitution is 0.5?
Answer:
Here, e =0.5
Let the ball fall from a height h1 from point A and rebound to B at a height of h₂.
∴ h₁ = 2 m

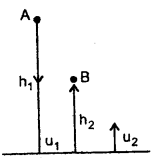
∴ If u₁ be the velocity on reaching the ground = velocity of approach and u₂ = Velocity on leaving the ground = velocity of separation

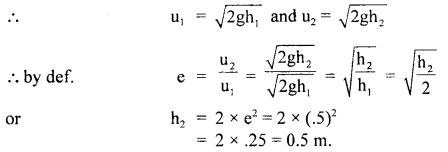
Question 11.
What percentage of K.E. of a moving particle is transferred to the stationary particle of
(a) 9 times it’s mass
Answer:
Let m₁ = mass of moving particle = m
and m₂ = mass of stationary particle = 9 m
and their velocities are u₁ and u₂ = 0 (given)
v₂ = velocity of the stationary particle after the collision.

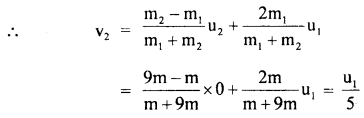
So, % of K.E. transferred to the stationary particle

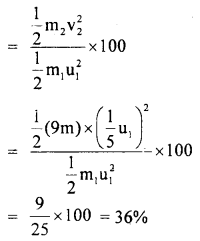
(b) equal mass,
Answer:

(c) \(\frac{1}{9}\) th of its mass.
Answer:

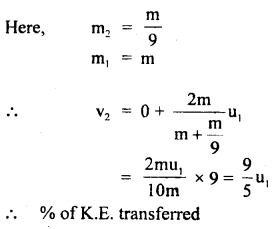
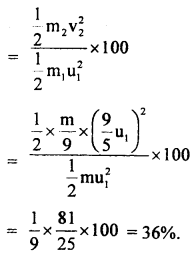
Question 12.
Calculate the work done in raising a stone of mass 6 kg of specific gravity 2 immersed in water from a depth of 4 m to 1 m below the surface of the water. Take g = 10 ms^-2.
Answer:
Here, m = 6 kg
∴ weight of stone = 6 × 10 = 60 N
specific gravity of stone = 2
∴ d = density of stone
= 2 × lg cm^-3
= 2g cm^-3.

∴ volume of stone = \(\frac{\mathrm{m}}{\mathrm{d}}=\frac{6 \times 1000 \mathrm{~g}}{2 \mathrm{gcm}^{-3}}\) = 3000 cm3
= 3000 × 10^-6 m³
= 3 × 10^-3 m³
= volume of displaced water.

Weight of water displaced or upward thrust on the stone
= volume × density of water × g
= 3 × 10^-3 × 1000 × 10 = 30 N

∴ The net force acting on the stone = weight of stone – upward thrust on the stone
or F = 60 – 30 = 30 N
Distance through which stone is raised = (4 – 1 )m = 3m
∴ work done, W = FS = 30 × 3 = 90 J.

Question 13.
An antenna radiates energy for 24 hours at the rate of 1 kW. Calculate the equivalent mass for radiated energy.
Answer:

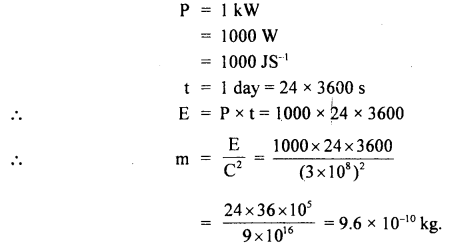
Question 14.
A particle moves from position r₁ = 3î + 2ĵ – 6k̂ to position r₂ = 14î + 13ĵ – 9k̂ under the action of a force (4î + ĵ + 3k̂)N. Calculate the work done.
Answer:
Here, F = (4î + ĵ + 3k̂)N
Displacement of the particle,

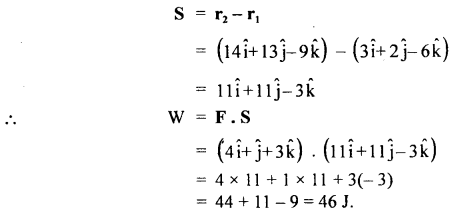
Question 15.
The displacement x of a particle moving in one dimension under the action of a constant force is related to the time by the equation t = \(\sqrt{x}\) + 3.
where x is in meters and t is in seconds.
Find (i) the displacement of the particle when its velocity is zero and
(ii) work is done by force in the first six seconds.
Answer:

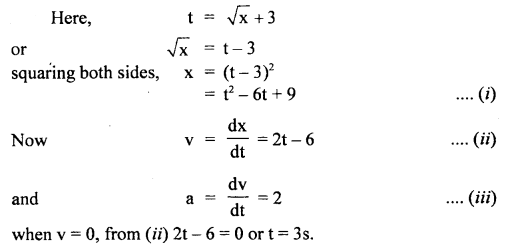
Question 16.
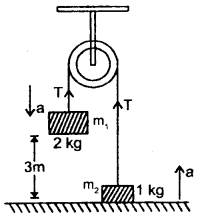
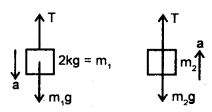
A 1 kg mass on a floor is connected to a 2 kg mass by a string passing over a pulley as shown in the figure. Obtain the speed of the masses (after they are released) when the 2 kg mass just touches the floor. Show that the gain in kinetic energy of the system equals the loss in its potential energy. The 2 kg mass is initially at a height 3 m above the ground.
Answer:
Here, m₂ = 1kg
m₁ = 2kg
u = 0
h = 3m
The system is shown in the figure. According to Newton’s Second law of motion, the equation of motion for 2 kg mass is
mg – T = ma
or
2 × 9.8 – T = 2a …(i)


(Free body diagrams of m₁ and m₂)

Since both the masses are initially at rest, therefore initial K.E. of the system = 0
Final K.E. of the system

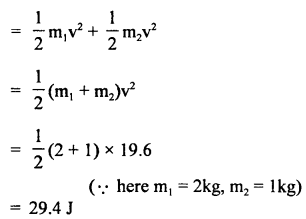
∴ Gain in K.E. = 29.4 – 0 = 29.4 J
Initially P.E. of the system = m₁gh₁ + m₂gh₂
= 2 × 9.8 × 3 + 1 × 9.8 × 0
= 58.8 J ( ∵ here h₂ = 0)

Finally, the 2 kg reaches the floor and mass 1 kg is at a height of 3m.
∴ Final P.E. of the system = m₁gh₁ + m₂gh₂
= m₁g × 0 + 1 × 9.8 × 3
= 29.4 J

∴ Loss of P.E. = 58.8 – 29.4
= 29.4 J
Thus Gain in K.E. = Loss of P.E. = 29.4 J.

Question 17.
A homogeneous and inextensible chain of length 2 m and mass 100 g lies on a smooth table, A small portion of the chain of length 0.5 m hangs from the table. Initially, the part of the chain lying on the table held and then released. Calculate the velocity with which the chain leaves the table, g = 10 ms’2.
Answer:
Mass of chain, M = 100 g = 0.1 kg
length of chain, l = 2 m

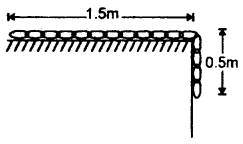
∴ Mass per unit length of the chain, m = \(\frac{M}{l}\)


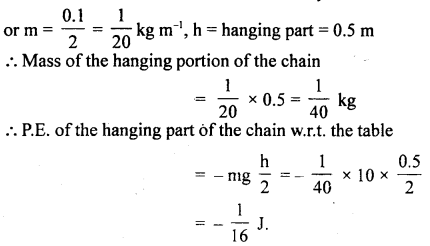
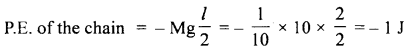
Let v = velocity of the chain when it leaves the table.

Question 18.
The K.E. of a body increases by 300%. How much linear momentum of the body will increase?
Answer:

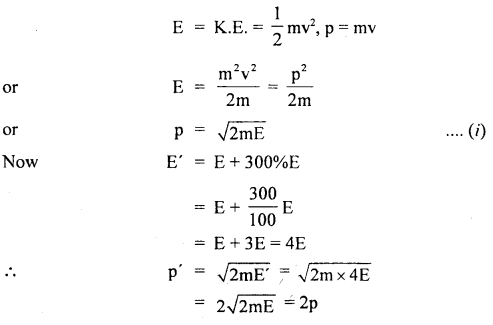
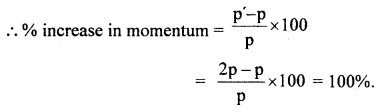
Question 19.
A ball falls under gravity from a height of 10m with an initial downward velocity of u. It collides with the ground, loses 50% of its energy in the collision, and then rises back to the same height. Find the initial velocity u.
Answer:
Here, u = initial velocity of the ball
h = its height

Let M = mass of the ball
∴ The total initial energy of the ball at height h,

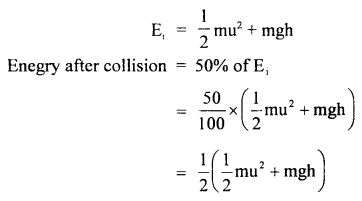
The ball rises to height h due to this energy.
∴ P.E. of ball = mgh
∴ According to the law of conservation of energy

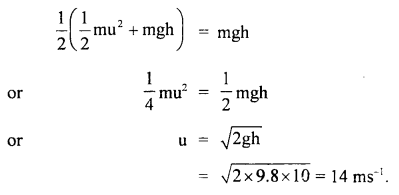
Question 20.
The heart of a man pumps 4-liter blood per minute at a pressure of 130 mm of mercury. If the density of mercury is 13.6 gm cm³, then calculate the power of the heart.
Answer:
Here, the height of the mercury column,

Question 21.
A body is allowed to fall from a height of 100 m. Find the increase in temperature of the body on reaching the ground if the whole of heat produced remains in the body. Given that the specific heat of the body = 0.2, J = 4.2 J cal^-1.
Answer:
Loss in P.E. of the body in falling through 100 m = m × 9.8 × 100 J = \(\frac{980 \mathrm{~m}}{4.2}\) (∵ P.E = mgh)

This loss is transformed into the heat state of the body = ms θ
where θ = rise in temperature.

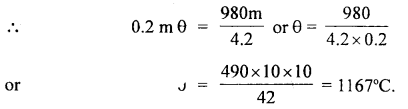
Question 22.
A truck of mass 2000 kg has a velocity of 8 ms^-1 when it starts from a point to descend a slope 200 m long. The vertical height of the slope is 18 m and the truck arrives at the bottom with a velocity of 20 ms^-1. Calculate the resistance offered.
Take g = 10 ms^-2.

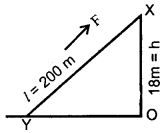
Answer:
Here, l = XY = length of slope.
= 200 m
OX = h = 18 m
Let u and v be the velocities of the .truck at points X and Y respectively.

Question 23.
A body of mass m slowly hauled up the hill by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force if the height of the hill is h, the length of its base is l, and the coefficient of friction is μ.

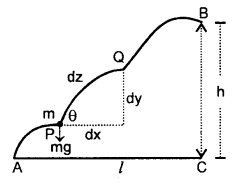
Answer:
Let PQ be the plane patch of the hill
dz = its length inclined at an angle θ with the horizontal

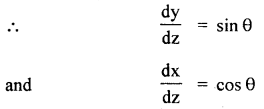
Force required to move the mass from P to Q
= mg sin θ + μmg cos θ

∴ Work done from P to Q = mg (sin θ + μcos θ).

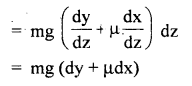
∴ W = total work done in moving the mass m from A to B is given by

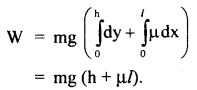
Question 24.
A chain of mass m and length l lying on a rough table starts sliding off the table all by itself till the hanging part equals n. Calculate the total work performed by the friction forces acting on the chain by the moment it slides off the table completely.
Answer:
Weight of suspended chain = n mg
weight of the part of the chain on the table = (1 – n) mg

Let μ = coefficient of friction of tabletop.
For sliding motion of the chain on the tabletop under the weight of’ the hanging chain,
μ(l – n) mg = n mg
or
μ = \(\frac{n}{1 – n}\) …(i)

The initial force of friction when the chain is pulled on the tabletop
= μ(1 – n)mg

Final force, when all the chain has been pulled = 0
mean friction = \(\frac{\mu(1-n) m g}{2}\)

Distance for which the chain is pulled = – (1 – n)l
∴ W = mean force × distance

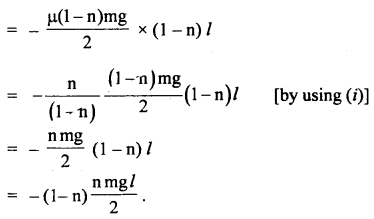
Question 25.
A flexible chain of length l and mass m is slowly pulled up at a constant speed over the edge of a table by a force F(x) parallel to the edge of the tabletop. Calculate the work done by F(x).
Answer:
Here the force required to pull the chain over the table varies with distance.
It is equal to the weight of the fraction of the chain \(\frac{(l-\mathrm{x})}{l}\)still hanging over the edge.

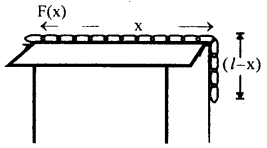
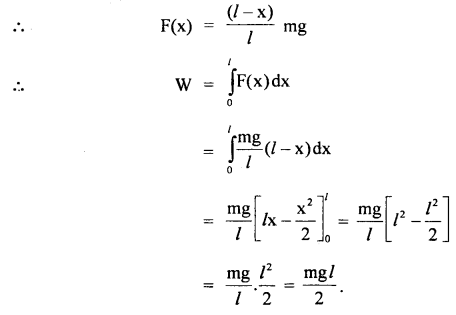
Value-Based Type:

Question 1.
Rajesh and Rakesh are two friends who participated in a quiz contest. The teacher asked Ramesh to lift a 20 kg weight vertically upwards to a height of 10 m and Rekcsh asked to pull 20 kg of weight by a rope over a pulley from a depth of 10 m from a well. There was a prize for one who will do more work. Rajesh claimed that he has done more work than Rakesh because he has not used any kind of lever. The teacher told Rajesh that he has done zero work but Rakesh has done the work. Hence, the prizes were given to Rakesh
(i) Why the teacher told that Rajesh did not do any work? justify your answer.
Answer:

1. The teacher wanted to check the knowledge of physics and awareness in a playful manner.
   He used the demonstration method to create interest.
2. We know that:
   W = F d cos θ
   In the case of Rajesh:
   θ = 90° and cos 90°=o
   ∴ work done(w) =Fd × o = o
   Hence, no work was done.

Question 2.
Shikha is doing her Engineering from IIT Delhi. Her mother was also an Engineer who wanted to check the knowledge of her daughter. She asked a question as to under. “If we assume that the moon orbits around the earth is perfectly circular then the earth’s gravitational force does no work. Is it correct?”
She explained that the moon’s displacement is tangential Whereas the earth’s force is inwards and θ = \(\frac{π}{2}\)
So, W = F.d. cos \(\frac{π}{2}\) = o
(i) Which values are displayed by Shikha?
Answer:
Values displayed are:
Explanatory, intelligent, cooperative.

(ii) Why her mother asked such a question?
Answer:
Her mother wanted to test the knowledge and presence of mind of her daughter to ask such type of tricky questions.

Question 3.
Suraj went to Big Bazaar to purchase certain goods. There he has noticed an old lady struggling with her shopping. Immediately he showed her the lift and explained to her how it carries the load from one floor to the next. Even then the old lady was not convinced. Then Suraj took her in the lift and showed her how to operate it..That old lady was very happy.
(a) What values does Suraj possess?
Answer:
Suraj is sympathetic and also has the attitude of helping others. He has patience.

(b) An elevator can carry a maximum load if 1800 kg is mov¬ing up with a constant speed of 2 m/s, The frictional force opposing the motion is 4000 N. Determine the minimum power delivered by the motor to the elevator in watts as well as in horsepower.
Answer:
The downward force on the elevator is
F = mg + F_f = (1800 × 10) + 4000 = 22000 N

The motor must supply enough power to balance this force.
Hence P = F.V = 22000 × 2 = 44000 = 59 hp