The Solid State Class 12 Important Extra Questions Chemistry Chapter 1

Here we are providing Class 12 Chemistry Important Extra Questions and Answers Chapter 1 The Solid State. Class 12 Chemistry Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Chemistry Chapter 1 Important Extra Questions The Solid State

The Solid State Important Extra Questions Very Short Answer Type

Question 1.
A metal crystallises in a body centred cubic structure. If ‘a’ is the edge length of its unit cell, ‘r’ is the radius of the sphere. What is the relationship between ‘r’ and ‘a’? (CBSE Sample Paper 2017-18)
Answer:
r = \(\frac{\sqrt{3}}{4}\)a

Question 2.
If the radius of the octahedral void is ‘r’ and radius of the atoms in close packing is ‘R’. What is the relation between ‘r’ and ‘R’? (CBSE Sample Paper 2017-18)
Answer:
r = 0.414 R

Question 3.
How many octahedral voids are there in 1 mole of a compound having cubic closed packed structure? (CBSE Sample Paper 2007)
Answer:
4 mole

Question 4.
Write a feature which will distinguish a metallic solid from an ionic solid.
Answer:
Metallic solids are good conductors of heat and electricity whereas ionic solids are insulators in solid state but conductors in molten state and in aqueous solution.

Question 5.
Write a distinguishing feature of metallic solids.
Answer:
Metallic solids are good conductors of heat and electricity.

Question 6.
KF has ccp structure. Calculate the radius of the unit cell if the side of the cube or edge length is 400 pm. How many F ions and octahedral voids are there in the unit cell? (CBSE Sample Paper 2011)
Answer:
For ccp lattice,
r = \(\frac{a}{2 \sqrt{2}}=\frac{400}{2 \times 1.414}\) = 141.4 pm
There are four (4) F ions and four (4) octahedral voids per unit cell.

Question 7.
Which point defect in crystals lowers the density of a crystal?
Answer:
Schottky defect

Question 8.
What type of interactions hold the molecules together in a polar molecular solid?
Answer:
Dipole-dipole forces

Question 9.
Which stoichiometric defect in crystals increases the density of a solid? (CBSE Delhi 2012)
Answer:
Interstitial defect

Question 10.
What type of semiconductor is obtained when silicon is doped with arsenic? (C.B.S.E. 2010)
Answer:
n-type semiconductor

Question 11.
Define forbidden zone of an insulator. (C.B.S.E. Delhi 2008)
Answer:
The large energy gap between the filled valence band and the empty conduction band in an insulator is called forbidden zone.

Question 12.
How do metallic and ionic substances differ in conducting electricity? (C.B.S.E. 2009)
Answer:
Metallic solids conduct electricity in the solid state whereas ionic substances conduct electricity in molten state or in solution, or metallic substances conduct electricity through electrons while ionic substances conduct electricity through ions.

Question 13.
What is the coordination number of each type of ions in a rock salt type crystal structure? (C.B.S.E. Delhi 2008)
Answer:
C.N. of Na⁺ = 6, C.N. of Cl^– = 6.

Question 14.
What is meant by ‘doping’ in a semiconductor? (C.B.S.E. Delhi 2012)
Answer:
The process of introduction of small amounts of impurities in the lattice of the crystal is called doping.

Question 15.
How may the conductivity of an intrinsic semiconductor be increased? (C.B.S.E. Delhi 2012)
Answer:
The conductivity of an intrinsic semiconductor may be increased by adding an appropriate amount of suitable impurity. This process is called doping.

Question 16.
How many atoms constitute one unit cell of a face-centred cubic crystal? (C.B.S.E. Delhi 2013)
Answer:
Four

Question 17.
What type of magnetism is shown by a substance if magnetic moments of domains are arranged in the same direction? (C.B.S.E. Delhi 2016)
Answer:
Ferromagnetism

Question 18.
Out of NaCI and AgCI, which one shows Frenkel defect and why? (C.B.S.E. Delhi 2019)
Answer:
AgCI shows Frenkel defect. This is because of small size of Ag⁺ ions; these can fit into interstitial sites of Cl^– ions.

Question 19.
What type of stoichiometric defect is shown by ZnS and why? (C.B.S.E. Delhi 2019)
Answer:
Frenkel defect. This is caused due to the large difference in size of ions.

Question 20.
Why conductivity of silicon increases on doping with phosphorus? (CBSE Delhi 2019)
Answer:
When silicon is doped with phosphorus, an extra electron is introduced after forming four covalent bonds. This extra electron gets delocalised and serves to conduct electricity. Hence, conductivity increases.

The Solid State Important Extra Questions Short Answer Type

Question 1.
Calculate the number of unit cells in 8.1 g of aluminium if it crystallises in a face-centred cubic (fcc) structure. (Atomic mass of Al = 27 g mol^-1).
Answer:
Moles of aluminium = \(\frac{8.1}{27}\) mol
No. of atoms of Al in 8.1 g = \(\frac{8.1}{27}\) × 6.022 × 10²³
No. of atoms in fee unit cell = 4
No. of unit cells = \(\frac{8.1}{27} \times \frac{6.022 \times 10^{23}}{4}\)
= 4.5 × 10²²

Question 2.
Tungsten crystallises in body centred cubic unit cell. If edge of the unit cell is 316.5 pm, what is the radius of the tungsten atom? (CBSE Sample Paper 2017-18)
Answer:
If a is the edge length of bcc unit cell, then radius of an atom,
r = \(\frac{\sqrt{3}}{4}\)a
Here, a = 316.5 pm
∴ r = \(\frac{\sqrt{3}}{4}\) × 316.5 pm = 137.04 pm

Question 3.
Silver metal crystallises with a face centred cubic lattice. The length of the unit cell is found to be 4.077 × 10^-8 cm. Calculate atomic radius and density of silver. (Atomic mass of Ag = 108u, N_A = 6.02 × 10²³). (C.B.S.E. Sample Paper 2012)
Answer:
Edge length of unit cell, a = 4.077 × 10^-8 cm For fcc lattice, radius of an atom is related to edge length, a as:

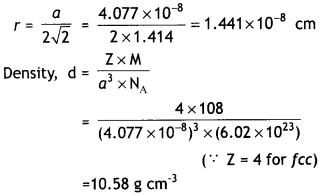
Question 4.
Analysis shows that FeO has a non- stoichiometric composition with molecular formula Fe_0.950. Give reason.
Answer:
It shows metal deficiency defect. In FeO, some Fe²⁺ ions are replaced by Fe³⁺ ions. Three Fe²⁺ ions are replaced by two Fe³⁺ ions to maintain electrical neutrality.

Question 5.
Following is the schematic alignment of magnetic moments:

Identify the type of magnetism. What happens when these substances are heated? (CBSE Sample Paper 2017-18)
Answer:
Ferrimagnetism. These substances lose ferrimagnetism on heating and become paramagnetic.

Question 6.
Identify the type of defect shown in the following figure:
What type of substances show this defect? (CBSE Sample Paper 2017-18)

Answer:
Schottky defect.
This type of defect is shown by ionic compounds in which
(i) the ions have high coordination number and
(ii) ions (cations and anions) are of almost similar sizes.

Question 7.
Classify each of the following as being either a p-type or n-type semiconductor:
(i) Ge doped with In.
(ii) Si doped with B. (CBSE Sample Paper 2011)
Answer:
(i) Ge belongs to group 14 and In belongs to group 13.
Therefore, an electron deficient hole is created and it is a p-type semiconductor.

(ii) B belongs to group 13 and Si belongs to group 14. Therefore, an electron deficient hole is created and it is a p-type semiconductor.

Question 8.
Give reason:
(a) Why is Frenkel defect found in AgCI?
(b) What is the difference between phosphorus doped and gallium doped silicon semiconductors? (CBSE Sample Paper 2011)
Answer:
(a) Due to small size of Ag⁺ ion, it can fit into interstitial sites.
(b) Phosphorus doped silicon is n-type semiconductor while gallium doped silicon is p-type semiconductor.

Question 9.
Why does LiCl acquire pink colour when heated in Li vapours? (CBSE Sample Paper 2011)
Answer:
On heating LiCl in Li vapours, the excess of Li atoms deposit on the surface of the crystal. The CT ions diffuse to the surface of the crystal and combine with Li atoms to form LiCl. The electrons produced by ionisation of Li atoms diffuse into the crystal and get trapped at anion vacancies called F-centres. These absorb energy from visible light and radiate pink colour.

Question 10.
Write a feature which will distinguish a metallic solid from an ionic solid. (C.B.S.E. Delhi 2010, 2012)
Answer:
Metallic solids are good conductors of heat and electricity whereas ionic solids are insulators in solid state but conductors in molten state and in aqueous solution.

Question 11.
Crystalline solids are anisotropic in nature. What does this statement mean? (C.B.S.E. Delhi 2011)
Answer:
This means that crystalline solids have different physical properties such as electrical resistance or refractive index in different directions. This is because of different arrangement of particles in different directions.

Question 12.
What are n-type semiconductors? (C.6.S.E. Delhi 2012)
Answer:
These are the semiconductors in which the current is carried by the electrons in the normal way. For example, germanium doped with impurity containing five valence electrons (e.g., P).

Question 13.
What is the formula of a compound in which the element Y forms hep lattice and atoms of X occupy 2/3rd of tetrahedral voids? (C.B.S.E. 2015)
Answer:
Atoms Y adopt hep arrangement and there are two tetrahedral sites per atom of Y. Since 2/3rd tetrahedral sites are occupied by atoms of X, then for each atom of Y, the number of X atoms will be = 2 × \(\frac{2}{3}=\frac{4}{3}\)
Formula of compound – X_4/3Y or X₄Y₃

Question 14.
Define the following terms in relation to crystalline solids:
(i) Unit cell
(ii) Coordination number
Give one example in each case. (C.B.S.E. 2011)
Answer:
(i) Unit cell is the smallest portion of a crystal lattice which when repeated over and over again in different directions results in the entire lattice. For example, simple cubic unit cell.

(ii) The number of nearest neighbours in a packing is called coordination number. For example, in a body centred cubic structure, the coordination number is eight.

Question 15.
Account for the following:
(i) Schottky defects lower the density of related solids.
(ii) Conductivity of silicon increases on doping it with phosphorus. (C.B.S.E. 2013)
Answer:
(i) In Schottky defect, there are holes due to missing cations and anions. Due to the presence of holes in solid, the density decreases.

(ii) Pure silicon has a network lattice in which all the four valence electrons are bonded to four other atoms. Therefore, it is an insulator. However, when silicon is doped with phosphorus having five valence electrons, the impurity leads to excess of electrons after forming four covalent bonds like silicon. The extra electrons serve to conductivity and therefore, the conductivity of silicon doped with phosphorus increases.

Question 16.
(i) What type of non-stoichiometric point defect is responsible for the pink colour of LiCl?
Answer:
Metal excess defect due to anion vacancies filled by free electrons i.e. F-centres.

(ii) What type of stoichiometric defect is shown by NaCI?
Answer:
Schottky defect.

OR

How will you distinguish between the following pairs of terms:
(i) Tetrahedral and octahedral voids
Answer:
Tetrahedral void is surrounded by 4 constituent particles (atoms, molecules or ions). Octahedral void is surrounded by 6 constituent particles (atoms, molecules or ions).

(ii) Crystal lattice and unit cell? (C.B.S.E. 2014)
Answer:
A regular three dimensional arrangement of points in space is called crystal lattice.
The smallest repeating pattern in crystal lattice which when repeated in three dimensional space gives the entire lattice is called the unit cell.

Question 17.
The well known mineral fluorite is chemically calcium fluoride. It is known that in one unit cell of this mineral there are 4 Ca²⁺ ions and 8 F^– ions and that Ca²⁺ ions are arranged in a fcc lattice. The fluoride ions fill all the tetrahedral holes in the face centred cubic lattice of Ca²⁺ ions. The edge of the unit cell is 5.46 × 10^-8 cm in length. The density of the solid is 3.18 g cm^-3. Use this information to calculate Avogadro’s number. (Molar mass of CaF₂ = 78.08 g mol”1) (C.B.S.E. Delhi 2010)
Answer:
Density, d = \(\frac{Z \times M}{a^{3} \times N_{A}}\)
d = 3.18 g cm^-3, M = 78.08 g mol^-1
a = 5.46 × 10^-8 cm
Since the lattice is fcc, Z = 4
Substituting the values,

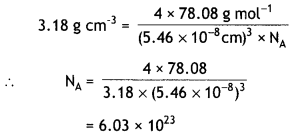
Question 18.
The density of copper metal is 8.95 g cm^-3. If the radius of copper atom be 127.8 pm, is the copper unit cell simple cubic, body centred cubic or face centred cubic? (C.B.S.E. 2010, C.B.S.E. Delhi 2010) ZxM
Answer:
Density, d = \(\frac{Z \times M}{a^{3} \times N_{A}}\)
Assuming fcc lattice for copper
a = 2√2 r
= 2 × 1.414 × 127.8 × 10^-10 cm
∴ a³ = (2 × 1.414 × 127.8 × 10^-10 cm)³
= 4.721 × 10^-23 cm³
∴ d = \(\frac{4 \times 63.54}{4.721 \times 10^{-23} \times 6.02 \times 10^{23}}\)
= 8.94 g cm^-3
Since the density is same as observed, the lattice is fcc lattice.

Question 19.
An element with density 10 g cm^-3 forms a cubic unit cell with edge length of 3 × 10^-8 cm. What is the nature of the cubic unit cell if the atomic mass of the element is 81 g mol^-1? (C.B.S.E. 2015)
Answer:
Density, d = \(\frac{z \times M}{a^{3} \times N_{A}}\)
d = 10 g cm^-3, M = 81 g mol^-1
a³ = (3 × 10^-8 cm)³
= 27 × 10^-24 cm³
N_A = 6.022 × 10²³
Therefore, 10 = \(\frac{Z \times 81}{\left(27 \times 10^{-24}\right) \times 6.022 \times 10^{23}}\)
Z = \(\frac{10 \times 27 \times 10^{-24} \times 6.022 \times 10^{23}}{81}\)
= 2.007
Nature of cubic unit cell = bcc

Question 20.
Aluminium crystallises in a fcc structure. Atomic radius of the metal is 125 pm. What is the length of the side of unit cell of the metal? (C.B.S.E. Delhi 2019C)
Answer:
For fcc,
r = \(\frac{a}{2 \sqrt{2}}\)
a = 2r × √2 = 2 × 125 pm × 1.414 = 353.5 pm

Question 21.
Answer the following:
(a) What is the formula of a compound in which element Y forms ccp lattice and atom X occupy \(\frac{1}{3}\)rd of tetrahedral voids?
(b) What type of non-stoichiometric point defect leads to colour in alkali metal halides? (C.B.S.E. Delhi 2019C)
Answer:
(a) X₂Y₃
(b) Metal excess defect due to anionic vacancies / F-centres.

Question 22.
(a) Atoms of element B form hep lattice and those of the element A occupy \(\frac{2}{3}\)rd of octahedral voids. What is the formula of the compound formed by the elements A and B?
(b) What type of stoichiometric defect is shown by ZnS and why? (C.B.S.E. Delhi 2019C)
Answer:
(a) A₂B₃
(b) Frenkel defect, due to small size of Zn²⁺ ion.

Question 23.
What happens when AgCl is doped with CdCl₂? What is the name of this defect?
OR
What type of defect is shown by NaCl in
(a) stoichiometric defects, and
(b) non-stoichiometric defects? (C.B.S.E. Delhi 2019C)
Answer:
When CdCl₂ is added to AgCl, it introduces impurity defect. The addition of one Cd²⁺ ion will replace two Ag⁺ ions to maintain electrical neutrality. One of the position of Ag⁺ ions will be occupied by Cd²⁺ ion and other will be left as a hole. Thus, cationic vacancies are produced. This is called impurity defect.
OR
(a) In stoichiometric defects: Schottky defect.
(b) In non-stoichiometric defects: Metal excess due to anionic vacancies.

The Solid State Important Extra Questions Long Answer Type

Question 1.
Copper crystallises with face centred cubic unit cell. If the radius of copper atom is 127.8 pm, calculate the density of copper metal. (Atomic mass of Cu = 63.55 u and Avogadro’s number, N_A = 6.02 × 10²³ mol^-1). (CBSE 2012)
Answer:
For a fcc unit cell, edge length (a) is related to radius of atom as:
r = \(\frac{a}{2 \sqrt{2}}\)
or a = 2√2.r = 2 × 1.414 × 127.8
= 361.42 pm
or = 361.42 × 10^-10 cm
Since the lattice is fcc, the number of copper atoms per unit cell, Z = 4.
Density, d = \(\frac{Z \times M}{a^{3} \times N_{A}}\)
M = 63.55 u, N_A = 6.02 × 10²³
∴ d = \(\frac{4 \times 63.55}{\left(361.42 \times 10^{-10}\right)^{3} \times\left(6.02 \times 10^{23}\right)}\)
= 8.94 g cm^-3

Question 2.
An element crystallises in a fcc lattice with cell edge of 250 pm. Calculate its density if 300 g of this element contain 2 × 10²⁴ atoms.
Answer:
Length of edge, a = 250 pm = 250 × 10^-12 m
= 250 × 10^-10 cm
Volume of unit cell = (250 × 10^-10 cm)³
= 15.625 × 10^-24 cm³
Mass of unit cell = No. of atoms in unit cell × Mass of each atom
Since the element has fcc arrangement, the number of atoms per unit cell, Z = 4
Mass of an atom = \(\frac{300}{2 \times 10^{24}}\) g
∴ Mass of unit cell = \(\frac{300}{2 \times 10^{24}}\) x 4
= 6.0 × 10^-22 g

Question 3.
An element with molar mass 27 g mol^-1 forms a cubic unit cell with edge length 4.05 × 10^-8 cm. If its density is 2.7 g cm^-3, what is the nature of the unit cell?
Answer:
Density of unit cell, d = \(\frac{\mathrm{Z} \times \mathrm{M}}{a^{3} \times \mathrm{N}_{\mathrm{A}}}\)
d = 2.7 g cm^-3, a = 4.05 × 10^-8 cm,
M = 27 g mol^-1, NA = 6.022 × 10²³

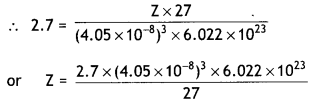
= 4.0
Since Z = 4, the unit cell is face centred cubic (fcc) unit cell.

Question 4.
An element with density 11.2 g cm^-3 forms a fee lattice with edge length of 4 × 10^-8 cm. Calculate the atomic mass of the element.
Answer:
Edge length of the unit cell
a = 4 × 10^-8 cm
Density = 11.2 g cm^-3
No. of atoms per unit cell in fcc lattice, Z = 4
Density, d = \(\frac{z \times M}{a^{3} \times N_{A}}\)
11.2 g cm^-3 = \(\frac{4 \times M}{\left(4 \times 10^{-8} \mathrm{~cm}\right)^{3} \times\left(6.02 \times 10^{23} \mathrm{~mol}^{-1}\right)}\)
or M = \(\frac{\left(11.2 \mathrm{~g} \mathrm{~cm}^{-3}\right) \times\left(4 \times 10^{-8} \mathrm{~cm}\right)^{3} \times\left(6.02 \times 10^{23} \mathrm{~mol}^{-1}\right)}{4}\)
= 107.9 g mol^-1
Atomic mass of element = 107.9 u.

Question 5.
The density of lead is 11.35 g cm^-3 and the metal crystallises with fcc unit cell. Estimate the radius of lead atom. (At. Mass of lead = 207 g mol^-1 and N_A = 6.02 × 10²³ mol^-1) (CBSE Delhi 2011)
Answer:
Let length of edge = a cm
Density = 11.35 g cm^-3
No. of atoms per unit cell in fcc Lattice = 4
Atomic mass, M = 207 g mol^-1
Density, d = \(\frac{Z \times M}{a^{3} \times N_{A}}\)

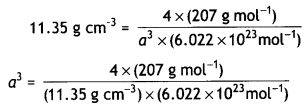
= 121.14 × 10^-24 cm³
Edge length, a = (121.14)^1/3 × 10^-8
= 4.948 × 10^-8 cm
or = 4.948 × 10^-10 m
or = 494.8 × 10^-12 m = 494.8 pm
Now, radius in fcc = \(\frac{a}{2 \sqrt{2}}\)
= \(\frac{494.8 \mathrm{pm}}{2 \times 1.414}\) = 174.96 pm

Question 6.
How can you determine the atomic mass of an unknown metal if you know its density and the dimension of its unit cell? Explain. (C.B.S.E. 2011)
Answer:
Consider a unit cell of edge a cm
Volume of unit cell = a³ cm³

Mass of unit cell = No. of atoms in a unit cell × Mass of each atom = Z × m …… (ii)
Mass of an atom present in a unit cell

Knowing density (d), edge length (a), number of atoms per unit cell (Z) and Avogadro’s number (6.02 × 10²³), atomic mass can be calculated.

Question 7.
ZnO turns yellow on heating. Why? (C.B.S.E. 2016)
Answer:
When ZnO is heated, it loses oxygen as:

The Zn²⁺ ions are entrapped in the interstitial sites and electrons are entrapped in the neighbouring interstitial sites to maintain electrical neutrality. This results in metal excess defect. Due to the presence of free electrons in the interstitial sites the colour is yellow.

Question 8.
(a) What type of semiconductor is obtained when silicon is doped with boron?
Answer:
(a) When silicon is doped with boron having three valence electrons, the bonds formed create electron deficient sites called holes. Under the influence of applied electric field, one electron from neighbouring atom moves to fill the hole but creates another hole at its own place. Therefore, the electrical conductance is due to movement of positive holes. Therefore, this type of semi-conductor is called p-type semi-conductor.

(b) What type of magnetism is shown in the following alignment of magnetic moments?
↑    ↑    ↑    ↑   ↑   ↑    ↑
Answer:
Ferromagnetic.

(c) What type of point defect is produced when AgCI is doped with CdCl₂? (C.B.S.E. Delhi 2013)
Answer:
CdCl₂ on adding to AgCl introduces impurity defect. The addition of one Cd²⁺ ion will replace two Ag⁺ ions to maintain electrical neutrality. One of the positions of Ag⁺ will be occupied by Cd²⁺ ion and the other will be left as a hole. Thus, a hole is created similar to Schottky defect.

Question 9.
Account for the following:
(i) Schottky defects lower the density of related solids.
Answer:
In Schottky defect, there are holes due to missing cations and anions. Due to the presence of holes in solid, the density decreases.

(ii) Conductivity of silicon increases on doping it with phosphorus. (C.B.S.E. 2013)
Answer:
Pure silicon has a network lattice in which all the four valence electrons are bonded to four other atoms. Therefore, it is an insulator. However, when silicon is doped with phosphorus (s²p³) having five valence electrons, the impurity leads to excess of electrons after forming four covalent bonds like silicon. The extra electrons serve to conductivity and therefore, the conductivity of silicon doped with phosphorus increases.

Question 10.
Examine the given defective crystal

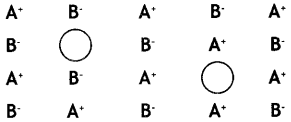
Answer the following questions:
(i) What type of stoichiometric defect is shown by the crystal?
Answer:
Schottky defect

(ii) How is the density of the crystal affected by this defect?
Answer:
Density of the crystal decreases.

(iii) What type of ionic substances show such defect? (C.B.S.E. Delhi 2014)
Answer:
Crystals having
(a) high coordination number and
(b) ions (cations and anions) of almost similar sizes. For example: KCl, KBr.

Question 11.
An element crystallises in a fcc lattice with edge length of 400 pm. The density of the element is 7 g cm^-3. How many atoms are present in 280 g of the element? (C.B.S.E. 2016)
Answer:
Edge length, a = 400 pm
= 400 × 10^-10 cm
Volume of unit cell = (400 × 10^-10)³
= 64 × 10^-24 cm^-3
Mass of element = 280 g
Density = 7 g cm^-3
Volume of 280 g of the element = \(\frac{280 \mathrm{~g}}{7 \mathrm{~g} \mathrm{~cm}^{-3}}\)
= 40 cm³
No. of unit cells in this volume
= \(\frac{40 \mathrm{~cm}^{3}}{64 \times 10^{-24} \mathrm{~cm}^{3}}\)
= 6.25 × 10²³ unit cells
Since the structure is fcc, number of atoms in a unit cell = 4
∴ No. of atoms in 280 g of element
= 4 × 6.25 × 10²³
= 2.5 × 10²⁴ atoms

Question 12.
An element crystallises in a fcc lattice with cell edge of 250 pm. Calculate the density of 300 g of this element containing 2 × 1024 atoms. (C.B.S.E. Delhi 2016)
Answer:
Length of edge, a = 250 pm = 250 × 10^-10 cm
Volume of unit cell = (250 × 10^-10)³
= 15.625 × 10^-24 cm³
Mass of unit cell = No. of atoms in unit cell × mass of each atom
Since the element has fcc arrangement, number of atoms per unit cell, Z = 4
Mass of an atom = \(\frac{300}{2 \times 10^{24}}\) = 1.50 × 10^-22 g

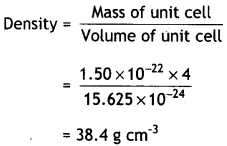
Question 13.
An element crystallises in fcc lattice with a cell edge of 300 pm. The density of the element is 10.8 g cm^-3. Calculate the number of atoms in 108 g of the element. (C.B.S.E. Delhi 2019)
Answer:
Edge length of the unit cell = 300 pm
= 300 × 10^-10 cm
Volume of unit cell = (300 × 10^-10) ³
= 27 × 10^-24 cm³
Mass of element = 108 g
Volume of 108 g element = \(\frac{108 \mathrm{~g}}{10.8 \mathrm{~g} \mathrm{~cm}^{-3}}\)
= 10 cm³
No. of unit cells = \(\frac{10}{27 \times 10^{-24}}\)
= 3.7 × 10²³ unit cells
Since the structure is fcc, number of atoms per unit cell = 4
Number of atom is 108 g = 3.7 × 10²³ × 4
= 1.48 × 10²⁴.

Question 14.
(a) An element crystallises in bcc lattice with a cell edge of 3 × 10^-8 cm. The density of the element is 6.89 g cm^-3. Calculate the molar mass of the element. (N_A = 6.022 × 10²³ mol^-1)
Answer:
Density of element, d = 6.89 gcm^-3
Cell edge, a = 3 × 10^-8 cm
Z = 2 (bcc)

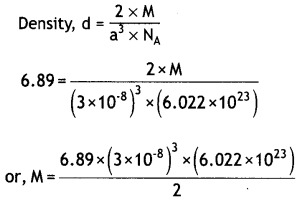
(b) What type of semiconductor is obtained when
(i) Ge is doped with In?
(ii) Si is doped with P? (C.B.S.E. 2019 Al)
Answer:
(i) p-type
(ii) n-type

Question 15.
(a) A compound is formed by two elements M and N. The element N forms ccp and M atoms occupy 1/3rd of tetrahedral voids. What is the formula of the compound?
(b) Which of the following lattices has the highest packing efficiency
(i) simple cubic
(ii) body centred cubic and
(iii) hexagonal close packed lattice?
(c) An element with molar mass 2.7 × 10^-2 kg mol^-1 forms a cubic unit cell with edge length 405 pm. If the density is 2.7 × 10³ kg m^-3. What is the nature of the cubic unit cell?
Answer:
(a) Since N forms ccp arrangement, it will have 4 atoms in a unit cell.
Number of N atoms in unit cell = 4
For each atom, there are two tetrahedral voids so that there are 8 tetrahedral voids per unit cell.
No. of M atoms = \(\frac{1}{3}\) × 8 = \(\frac{8}{3}\)
Formula = M_8/3N₄
or = M₂ N₃.

(b) The packing efficiencies are:
simple cubic = 52.4%
body centred cubic = 68%
hexagonal close packed = 74%
∴ Hexagonal close packed lattice has highest packing efficiency.

(c) Edge length = 405 pm = 405 × 10^-12 m
Density of the cell = 2.7 × 10^-3 kg m^-3
Molar mass = 2.7 × 10^-2 kg mol^-1

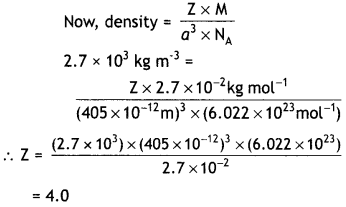
Since the unit cell contains 4 atoms, it is cubic close packed structure, ccp.

Question 16.
How will you distinguish between the following pair of terms:
(i) Hexagonal close packing and cubic close packing
(ii) Crystal lattice and unit cell.
(iii) Tetrahedral void and octahedral void.
Answer:
(i)

Hexagonal close packing	cubic close packing
(i) In hcp, the spheres of the third layer are exactly aligned with those of the first layer. This arrangement is represented as AB AB …………… type.	(i) In ccp, the spheres of the third layer are not aligned with those of the first layer or second layer. The layers of fourth layer are aligned with those of the first layer. This pattern is represented as ABC ABC ………
(ii) In hcp, the tetrahedral voids of the second layer may be covered by the spheres of the third layer.	(ii) In ccp, the third layer may be placed above the second layer in a manner such that its spheres cover the octahedral voids.

(ii) The three dimensional arrangement of constituent particles of a substance (atoms, ions or molecules) is called crystal lattice.
The smallest repeating pattern in a crystal lattice which when repeated in three dimensions gives the crystal is called unit cell.

(iii) A void surrounded by four spheres is called a tetrahedral void while a void surrounded by six spheres is called an octahedral void.

Question 17.
(i) How many lattice points are there in one unit cell of each of the following lattice?
(a) face centred cubic
(b) face centred tetragonal
(c) body centred.
Answer:
(i) (a) In face centred cubic arrangement, number of lattice points are:
8 (at corners) + 6 (at face centres)
Lattice points per unit celt
= 8 × \(\frac{1}{8}\) + 6 × \(\frac{1}{2}\) = 4

(b) In face centred tetragonal, number of lattice points are:
= 8 (at corners) + 6 (at face centres) Lattice points per unit cell 1 1
= 8 × \(\frac{1}{8}\) + 6 × \(\frac{1}{2}\) = 4

(c) In body centred cubic arrangement number of lattice points are:
= 8 (at corners) + 1 (at body center) Lattice points per unit cell
= 8 × \(\frac{1}{8}\) + 1 = 2

(ii) Explain: (a) The basis of similarities and differences between metallic and ionic crystals.
(b) Ionic solids are hard and brittle.
Answer:
(a) Basis of similarities
1. Both ionic and metallic crystals have electrostatic forces of attraction. In ionic crystals, these are between the oppositely charged ions while in metals, these are among the valence electrons and the kernels. That is why both ionic and metallic crystals have high melting points.
2. In both cases, the bond is non- directional.

Basis of differences
1. In ionic crystals, the ions are not free to move and therefore, they do not conduct electricity in the solid state. They conduct electricity in the molten state or in their aqueous solution. However, in metals, the valence electrons are free to move and hence they conduct electricity in the solid state.
2. Ionic bond in ionic crystals is strong due to electrostatic forces of attraction. However, metallic bond may be weak or strong depending upon the number of valence electrons and the size of the kernels.

(b) Ionic crystals are hard because there are strong electrostatic forces of attraction among the oppositely charged ions. They are brittle because the ionic bond is non-directional.

Question 18.
(a) If the radius of the octahedral void is r and radius of the atoms in close packing is R. Derive relation between r and R.
Answer:
A sphere of radius r filling in an octahedral void of spheres of radius R is shown in figure.

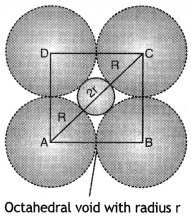
If the length of the unit cell is a cm, then
In right angled ∆ABC, AB = BC = a cm
The diagonal AC is:

Thus, for an atom to occupy an octahedral void, its radius must be 0.414 times the radius of the sphere.

(b) Copper crystallises into a fcc lattice with edge length 3.61 × 10^-8 cm. Show that the calculated density is in agreement with its measured value of 8.29 g cm^-3.
Answer:
Density, d = \(\frac{Z \times M}{a^{3} \times N_{A}}\)
For fcc lattice, Z = 4
Atomic mass, M of copper = 63.5 g/mol^-1
a = 3.61 × 10^-8 cm
∴ p = \(\frac{4 \times 63.5}{\left(3.61 \times 10^{-8}\right)^{3} \times 6.022 \times 10^{23}}\)
= 8.96 g cm^-3
This value is close to measured value.

Question 19.
What is a semiconductor? Describe the two main types of semiconductors and contrast their conduction mechanism.
Answer:
The substances whose conductance lies between that of conductors (metals) and insulators are called semiconductors. They have conductivity values ranging from 10^-6 to 10⁴Ω^-1m^-1. Two main types of semiconductors are n-type and p-type.

(i) n-type semiconductors: These are the semiconductors in which the current is carried by the electrons in the normal way. For example, silicon and germanium belong to group 14 of the periodic table and have four valence electrons each. In their crystals, each atom forms four covalent bonds with its neighbours.

When it is doped with an element of group 15 such as P or As, which contains five valence electrons, they occupy some of the lattice sites in silicon or germanium crystal. Four of the five valence electrons are used in the formation of four covalent bonds with the four neighbouring Si atoms and the fifth electron is extra and becomes delocalised.

This delocalised electron will be able to conduct electricity and such type of conduction is called n-type conduction. Hence silicon or germanium doped with extra electron of impurity are called n-type semiconductors.

(ii) p-type semiconductors: These are the semiconductors in which current is carried by the movement of positive holes. For example, when Ge or Si are doped with electron deficient atoms such as Ga or In (of Group 13) containing three valence electrons, the atoms of Ga or In will replace Ge atoms.

Each In or Ga atom will use its three electrons for forming three covalent bonds with neighbouring Ge atoms and the place for fourth bond will remain missing and is called electron vacancy or hole. Such holes can move through the crystals like a positive charge giving rise to conductivity. This type of conduction is called p-type conduction. Hence, Si or Ge doped with electron deficient atoms as impurity are called p-type semiconductors.

Question 20.
Explain the following with suitable examples:
(a) Ferromagnetism
(b) Paramagnetism
(c) Ferrimagnetism
(d) Anti-ferromagnetism
(e) 12-16 and 13-15 group compounds.
Answer:
(a) Ferromagnetism: When there is spontaneous alignment of magnetic moments of domains in the same direction, we get ferromagnetism. These have strong magnetic effects and ordering of domains persists even when magnetic field is removed and – ferromagnetic substance becomes permanent magnet.

(b) Paramagnetism: The substances which have permanent magnetic dipoles and are attracted by the magnetic field are called paramagnetic substances. This property of attraction by the magnetic field is known as paramagnetism. The paramagnetic substance are atoms, molecules or ions having unpaired electrons. For example, O₂, Cu²⁺, Fe²⁺, etc. They lose their magnetism in the absence of magnetic field.

(c) Ferrimagnetism: When the magnetic moments of the domains are aligned in parallel or anti-parallel directions in unequal numbers resulting in net magnetic moment, we get ferrimagnetism.

(d) Anti-ferromagnetism: It arises when the alignment of magnetic moments is in a compensatory way so that the resultant magnetic moment is zero (e.g., MnO).

(e) The solid binary compounds prepared by combining elements of group 12 and 16 are called 12-16 compounds. For example CdS, ZnS, etc. The compounds prepared by combining elements of group 13 and 15 are called 13-15 compounds. For example, AlP, GaAs, etc. These compounds are used as semiconductors.

Question 21.
Give the points of differences between Schottky defect and Frenkel defect ?
OR
Explain:
(i) Why is Frenkel defect not found in pure alkali metal halides ?
(ii) Zinc oxide is white but it turns yellow on heating.
(iii) CaCl₂ will introduce Schottky defect when added to AgCl crystal.
Answer:
The important differences between Schottky and Frenkel defects are given ahead:

Schottky defect	Frenkel defect
1. It is produced be cause of missing atoms or ions from their normal sites.	1. It is produced when some atoms or ions leave their normal sites and occupy interstitial sites.
2. The presence of Schottky defect lowers the density of the crystal.	2. It does not affect the density of the crystal.
3. It is generally exhibited by ionic solids having high coordination number and in which cations and anions are of equal size. e.g., NaCl, CsCl.	3. It is generally exhibited by ionic solids having low coordination number and in which anions are larger in size than cation e.g., ZnS, AgCl.

OR
(i) Frenkel defect is not found in pure alkali metal halides because the ions cannot get into the interstitial sites due to their larger size.

(ii) When ZnO is heated it loses oxygen as:

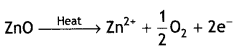
The Zn²⁺ ions are entrapped in the interstitial sites and electrons are entrapped in the neighbouring interstitial sites to maintain electrical neutrality. This results in metal excess defect. Due to the presence of free electrons in the interstitial sites the colour is yellow.

(iii) CaCl₂ on adding to AgCl introduces impurity defect. The addition of one Ca²⁺ ion will replace two Ag⁺ ions to maintain electrical conductivity. One of the position of Ag⁺ will be occupied by Ca²⁺ ion and other will be left as a hole. Thus, a hole is created similar to Schottky defect.

Question 22.
What do you understand by a space lattice and a unit cell?
Answer:
(a) Space lattice is a regular arrangement of the constituent particles (atoms, ions or molecules) of a crystalline solid in three dimentional space.

The positions which are occupied by atoms, ions or molecules in the crystal lattice are called lattice points or lattice sites. A two dimensional and a three dimensional space lattice is shown in Fig. 1 (a) and 1 (b) respectively.


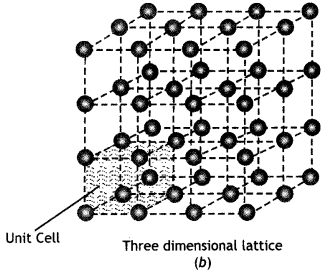
Fig. 1. (a) Two dimensional and
(b) Three dimensional space lattice.

A unit cell is the smallest repeating unit in space lattice which when repeated over and over again results in the crystal of the given substance. The unit cell gives the shape of the entire crystal. The crystal may be considered to consist of an infinite number of unit cells. The unit cell in the above crystal lattice [Fig. 1 (b)] is shown in The complete crystal lattice can be obtained by extending the unit cell in all the three directions.

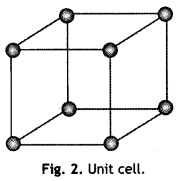
Question 23.
What are tetrahedral and octahedral holes (voids) in close packed stacks of spheres? Explain.
Answer:
Tetrahedral and octahedral holes. The close packed arrangement of spheres has two types of holes or voids:
Tetrahedral holes: Tetrahedral hole Is produced when one sphere rests upon three other touching spheres. The space which is left between these touching spheres is called tetrahedral hole or tetrahedral site. The tetrahedral hole is shown in Fig. (a). It may be noted that in close packed arrangement (ccp or hcp), there are twice as many tetrahedral holes as there are spheres.

Octahedral hole.: This type of hole is formed at the centre of six spheres which form a regular octahedral. This is shown in Fig. (b). From the figure, it is clear that the octahedral hole is formed by two sets of equilateral triangles which point in opposite directions. It may be noted that there are same number of octahedral holes as the number of spheres.

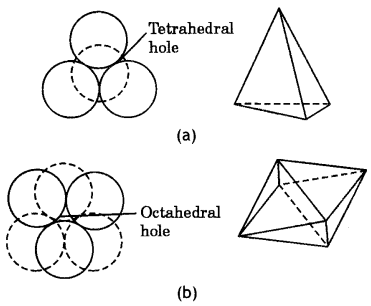
Fig. (a) Tetrahedral hole (b) Octahedral hole.

Question 24.
(a) Why does table salt, NaCl, some times appear yellow in colour?
(b) Why is FeO(s) not formed in stoichiometric composition?
(c) Why does white ZnO (s) becomes yellow upon heating?
Answer:
(a) The yellow colour of sodium chloride crystals is due to metal excess defect. In this defect, the unpaired electrons get trapped in anion vacancies. These sites are called F-centres. The yellow colour results by excitation of these electrons when they absorb energy from the visible light falling on the crystals.

(b) In the crystals of FeO, some of the Fe²⁺ cations are replaced by Fe³⁺ ions. To balance the charge, three Fe²⁺ ions are replaced by two Fe³⁺ ions to make up for the loss of positive charge. As a result, there would be less amount of metal as compared to stoichiometric proportion.

(c) When ZnO is heated it loses oxygen as:

The Zn²⁺ ions are entrapped in the interstitial sites and electrons are entrapped in the neighbouring interstitial sites to maintain electrical neutrality. This results in metal excess defect and F-centres are created. Due to the presence of electrons in the interstitial voids, the colour is yellow.

Question 25.
(a) Explain why does conductivity of germanium crystals increase on doping with gallium.
(b) In a compound, nitrogen atoms (N) make cubic close packed lattice and metal atoms (M) occupy one-third of the tetrahedral voids present. Determine the formula of the compound formed by M and N?
(c) Under which situations can an amorphous substance change to crystalline form?
Answer:
(a) On doping germanium with gallium, some of the positions of lattice of germanium are occupied by gallium. Gallium atom has only three valence electrons. Therefore, fourth valency of nearby germanium atom is not satisfied and this site remains vacant. This place is deficient of electrons and is called electron hole or electron vacancy.

Electron from neighbouring atom moves to fill the gap, thereby creating a hole in its original position. Under the influence of electric field, electrons move towards positively charged plates through these holes and conduct electricity. The holes appear to move towards negatively charged plates. The movement of electrons (or electron holes) results in increase in conductivity of germanium.

(b) N atoms make up ccp arrangement and there are two tetrahedral sites per atom of N.
No. of N atoms per unit cell = 4
No. of tetrahedral sites = 4 × 2 = 8
No. of sites occupied by M = \(\frac{1}{3}\) × 8 = \(\frac{8}{3}\)
∴ No. of M atoms per unit cell = \(\frac{8}{3}\)
Formula M_8/3N₄ or M₈N₁₂ or M₂N₃

(c) On heating, amorphous solids become crystalline at some temperature. For example, some glass objects from ancient civilisations are found to become milky in appearance because of some crystallisation.