Relations and Functions Class 12 Important Extra Questions Maths Chapter 1

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 1 Relations and Functions. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 1 Important Extra Questions Relations and Functions

Relations and Functions Important Extra Questions Very Short Answer Type

Question 1.
If R = {(x, y) : x + 2y = 8} is a relation in N, write the range of R.
Solution:
Range of R = {1, 2, 3}.
[∵ When x = 2, then y = 3, when x = 4, then y = 2, when x = 6, then y = 1 ]

Question 2.
Show that a one-one function :
f{1, 2, 3} → {1, 2, 3} must be onto.   (N.C.E.R.T.)
Solution:
Since ‘f’ is one-one,
∴ under ‘f’, all the three elements of {1, 2, 3} should correspond to three different elements of the co-domain {1, 2, 3}.
Hence, ‘f’ is onto.

Question 3.
What is the range of the function f(x) = \(\frac{|x-1|}{x-1}\) ? (C.B.S.E. 2010)
Solution:
When x > 1,
than f(x) = \(\frac{x-1}{x-1}\) = 1.
When x< 1,
than f(x) = \(\frac{-(x-1)}{x-1}\) = -1
Hence, R_f = {-1, 1}.

Question 4.
Show that the function f : N → N given by f(x) = 2x is one-one but not onto. (N.C.E.R.T.)
Solution:
Let x₁, x₂ ∈ N.
Now, f(x₁) = f(x₂)
⇒ 2x₁ = 2x₂
⇒ x₁ = x₂
⇒ f is one-one.
Now, f is not onto.
∵ For 1 ∈ N, there does not exist any x ∈ N such that f(x) = 2x = 1.
Hence, f is ono-one but not onto.

Question 5.
If f : R → R is defined by f(x) = 3x + 2 find f(f(x)). C.B.S.E. 2011 (F))
Solution:
f(f(x)) = 3 f(x) + 2
= 3(3x + 2) + 2 = 9x + 8.

Question 6.
If f(x) = \(\frac{x}{x-1}\) , x ≠1 then find fof. (N.C.E.R.T)
Solution:

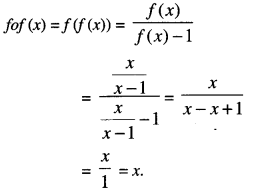
Question 7.
If f: R → R is defined by f(x) = (3 -x³)^1/3, find fof(x)
Solution:
fof(x) = f(f(x)) = (3-(f(x))³)^1/3
= (3 – ((3 – x³)^1/3)³)^1/3
= (3 – (3 – x³ ))^1/3= (x³)^1/3 = x.

Question 8.
Are f and q both necessarily onto, if gof is onto? (N.C.E.R.T.)
Solution:
Consider f: {1, 2, 3, 4} → {1, 2, 3, 4}
and g : {1, 2, 3,4} → {1,2.3} defined by:
f(1) = 1, f(2) = 2, f(3) = f(4) = 3
g (1) = 1, g (2) = 2, g (3) = g (4) = 3.
∴ gof = g (f(x)) {1, 2,3}, which is onto
But f is not onto.
[∵ 4 is not the image of any element]

Relations and Functions Important Extra Questions Short Answer Type

Question 1.
Let A be the set of all students of a Boys’ school. Show that the relation R in A given by:
R = {(a, b): a is sister of b} is an empty relation and the relation R’ given by :
R’ = {(a, b) : the difference between heights of a and b is less than 3 metres} is an universal relation. (N.C.E.R.T.)
Solution:
(i) Here R = {(a, b): a is sister of b}.
Since the school is a Boys’ school,
∴ no student of the school can be the sister of any student of the school.
Thus R = Φ Hence, R is an empty relation.

(ii) Here R’ = {(a,b): the difference between heights of a and b is less than 3 metres}.
Since the difference between heights of any two students of the school is to be less than 3 metres,
∴ R’ = A x A. Hence, R’ is a universal relation.

Question 2.
Let f : X → Y be a function. Define a relation R in X given by :
R = {(a,b):f(a) = f(b)}.
Examine, if R is an equivalence relation. (N.C.E.R.T.)
Solution:
For each a ∈ X, (a, a) ∈ R.
Thus R is reflexive. [∵ f (a) = f(a)]
Now (a, b) ∈ R
⇒ f(a) = f(b)
⇒ f(b) = f (a)
⇒ (b, a) ∈ R.
Thus R is symmetric.
And (a, b) ∈ R
and (b, c) ∈ R
⇒ f(a) = f(b)
and f(b) = f(c)
⇒ f(a)= f(c)
⇒ (a, c) ∈ R.
Thus R is transitive.
Hence, R is an equivalence relation.

Question 3.
Let R be the relation in the set Z of integers given by:
R = {(a, b): 2 divides a – b}.
Show that the relation R is transitive. Write the equivalence class [0].   (C.B.S.E. Sample Paper 2019-20)
Solution:
Let 2 divide (a – b) and 2 divide (b – c), where a,b,c ∈ Z
⇒ 2 divides [(a – b) + (b – c)]
⇒ 2 divides (a – c).
Hence, R is transitive.
And [0] = {0, ± 2, ± 4, ± 6,…].

Question 4.
Show that the function :
f : N → N
given by f(1) = f(2) = 1 and f(x) = x -1, for every x > 2 is onto but not one-one. (N.C.E.R.T.)
Solution:
Since f(1) = f(2) = 1,
∴ f(1) = f(2), where 1 ≠ 2.
∴ ‘f’ is not one-one.
Let y ∈ N, y ≠ 1,
we can choose x as y + 1 such that f(x) = x – 1
= y + 1 – 1 = y.
Also 1 ∈ N, f(1) = 1.
Thus ‘f ’ is onto.
Hence, ‘f ’ is onto but not one-one.

Question 5.
Find gof and fog, if:
f : R → R and g : R → R are given by f (x) = cos x and g (x) = 3x². Show that gof ≠ fog. (N. C.E.R. T.)
Solution:
We have :
f(x) = cos x and g(x) = 3x².
∴ gof (x) = g (f(x)) = g (cos x)
= 3 (cos x)² = 3 cos² x
and fog (x) = f(g (x)) = f(3x²) = cos 3x².
Hence, gof ≠ fog.

Question 6.
If f(x) = \(\frac{4 x+3}{6 x-4}\) , x ≠ \(\frac{2}{3}\) find fof(x)
Solution:
We have: \(\frac{4 x+3}{6 x-4}\) …(1)
∴ fof(x) — f (f (x))

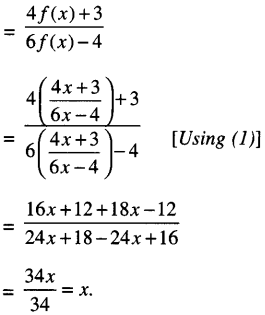
Question 7.
Let A = N x N be the set of ail ordered pairs of natural numbers and R be the relation on the set A defined by (a, b) R (c, d) iff ad = bc. Show that R is an equivalence relation.
Solution:
Given: (a, b) R (c, d) if and only if ad = bc.
(I) (a, b) R (a, b) iff ab – ba, which is true.
[∵ ab = ba ∀ a, b ∈ N]
Thus, R is reflexive.

(II) (a, b) R (c,d) ⇒ ad = bc
(c, d) R (a, b) ⇒ cb = da.
But cb = be and da = ad in N.
∴ (a, b) R (c, d) ⇒ (c, d) R (a, b).
Thus, R is symmetric.

(III) (a,b) R (c, d)
⇒ ad = bc …(1)
(c, d) R (e,f)
⇒ cf = de … (2)
Multiplying (1) and (2), (ad). (cf) – (be), (de)
⇒ af = be
⇒ (a,b) = R(e,f).
Thus, R is transitive.
Thus, R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation.

Question 8.
Let f: R → R be the Signum function defined as :

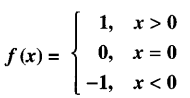
and g : R → R be the Greatest Integer Function given by g (x) = [x], where [x] is greatest integer less than or equal to x. Then does fog and gof coincide in (0,1] ?
Solution:
For x ∈ (0,1].

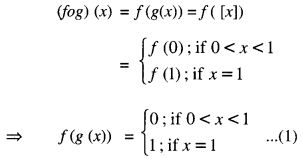
And (gof) (x) = g(f(x)) = g(1)
[∵ f(x) = 1 ∀ x > 0]
= [1] = 1
⇒ (gof) (x) = 1 ∀ x ∈ (0, 1] …(2)
From (1) and (2), (fog) and (gof) do not coincide in (0, 1].

Relations and Functions Important Extra Questions Long Answer Type 1

Question 1.
Show that the relation R on R defined as R = {(a, b):a ≤ b}, is reflexive and transitive but not symmetric.
Solution:
We have : R = {(a, b)} = a ≤ b}.
Since, a ≤ a ∀ a ∈ R,
∴ (a, a) ∈ R,
Thus, R reflexive.
Now, (a, b) ∈ R and (b, c) ∈ R
⇒ a ≤ b and b ≤ c
⇒ a ≤ c
⇒ (a, c) ∈ R.
Thus, R is transitive.
But R is not symmetric
[∵ (3, 5) ∈ R but (5, 3) ∉ R as 3 ≤ 5 but 5 > 3]

Question 2.
Prove that function f : N → N, defined by f(x) = x² + x + 1 is one-one but not onto. Find inverse of f: N → S, where S is range of f.
Solution:
Let x₁, x₂ ∈ N.
Now, f(x₁) = f(x₂)

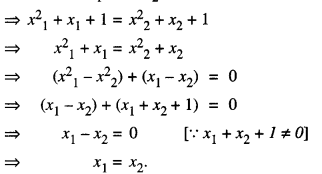
Thus, f is one-one.
Let y ∈ N, then for any x,
f(x) = y if y = x² + x + 1


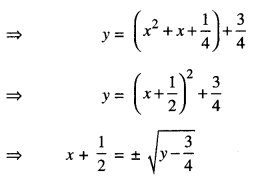
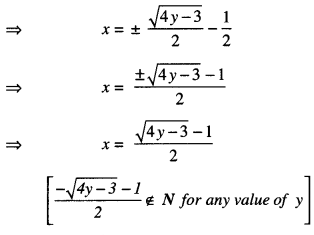
Now, for y = \(\frac{3}{4}\) , x = \(-\frac{1}{2}\) ∉ N.
Thus, f is not onto.
⇒ f(x) is not invertible.
Since, x > 0, therefore, \(\frac{\sqrt{4 y-3}-1}{2}\) > 0
⇒ \(\sqrt{4 y-3}\) > 1
⇒ 4y – 3 > 1
⇒ 4y > 4
⇒ y > 1.
Redefining, f : (0, ∞) → (1, ∞) makes
f(x) = x² + x + 1 on onto function.
Thus, f (x) is bijection, hence f is invertible and f^-1 : (1, ∞) → (1,0)
f^-1(y) = \(\frac{\sqrt{4 y-3}-1}{2}\)

Question 3.
Let A = (x ∈Z : 0 ≤ x ≤ 12}.
Show that R = {(a, b) : a, b ∈ A; |a – b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. Also write the equivalence class [2]. (C.B.S.E 2018)
Solution:
We have:
R = {(a, b): a, b ∈ A; |a – b| is divisible by 4}.
(1) Reflexive: For any a ∈ A,
∴ (a, b) ∈ R.
|a – a| = 0, which is divisible by 4.
Thus, R is reflexive.

Symmetric:
Let (a, b) ∈ R
⇒ |a – b| is divisible by 4
⇒ |b – a| is divisible by 4
Thus, R is symmetric.

Transitive: Let (a, b) ∈ R and (b, c) ∈ R
⇒ |a – b| is divisible by 4 and |b – c| is divisible by 4
⇒ |a – b| = 4λ
⇒ a – b = ±4λ ………….(1)
and |b – c| = 4µ
⇒ b – c = ± 4µ ………….(2)

Adding (1) and (2),
(a-b) + (b-c) = ±4(λ + µ)
⇒ a – c = ± 4 (λ + µ)
⇒ (a, c) ∈ R.
Thus, R is transitive.
Now, R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation.

(ii) Let ‘x’ be an element of A such that (x, 1) ∈ R
⇒ |x – 1| is divisible by 4
⇒ x – 1 = 0,4, 8, 12,…
⇒ x = 1, 5, 9, 13, …
Hence, the set of all elements of A which are related to 1 is {1, 5, 9}.

(iii) Let (x, 2) ∈ R.
Thus |x – 2| = 4k, where k ≤ 3.
∴ x = 2, 6, 10.
Hence, equivalence class [2] = {2, 6, 10}.

Question 4.
Prove that the function f: [0, ∞) → R given by f(x) = 9x² + 6x – 5 is not invertible. Modify the co-domain of the function f to make it invertible, and hence find f^-1.   (C.B.S.E. Sample Paper 2018-19)
Solution:
Let y∈ R.
For any x, f(x) = y if y = 9x² + 6x – 5
⇒ y = (9x² + 6x + 1) – 6
= (3x + 1)² – 6

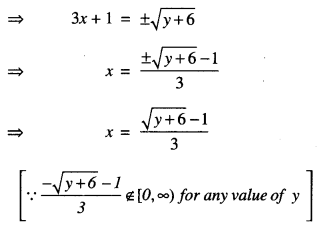
For y = – 6 ∈ R, x = \(-\frac{1}{3}\) ∉ [0, ∞).
Thus, f(x) is not onto.
Hence, f(x) is not invertible.

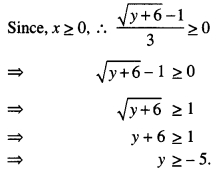
We redefine,
f: [0, ∞) → [-5, ∞),
which makes f(x) = 9x² + 6x – 5 an onto function.
Now, x₁, x₂ ∈ [0, ∞) such that f(x₁) = f(x₂)
⇒ (3x₁ + 1)² = (3x₂ + 1)²
⇒[(3x₁ + 1)+ (3x₂ + 1 )][(3x₁ + 1)- (3x₂ + 1)]
⇒ [3(x₁ + x₂) + 2][3(x₁ – x₂)] = 0
⇒ x₁ = x₂
[∵ 3(x₁ + x₂) + 2 > 0]
Thus, f(x) is one-one.
∴ f(x) is bijective, hence f is invertible
and f^-1: [-5, ∞) → [0, ∞)
f^-1 (y) = \(\frac{\sqrt{y+6}-1}{3}\)

Question 5.
Check whether the relation R in the set R of real numbers, defined by :
R = {(a, b): 1 + ab > 0}, is reflexive, symmetric or transitive.   (C.B.S.E. Sample Paper 2018-19)
Solution:
R = {(a, b): 1 + ab> 0}.

Reflexive:
Now, 1 + a.a = 1 + a² > 0
⇒ (a, a) ∈ R ∀ a ∈ R.
Thus, R is reflexive.

Symmetric:
Let (a, b) ∈ R.
Then 1 + ab > 0
⇒ 1 + ba > 0
⇒ (b, a) ∈ R.
Thus, R is symmetric.

Transitive:
Take a = -8,b = -1, c = \(\frac { 1 }{ 2 }\)
Now, 1 + ab = 1 + (-8) (-1)
= 9 > 0
⇒ (a, b) ∈ R
and, 1 + bc = 1 + (-1)(\(\frac { 1 }{ 2 }\) )
= 1 – \(\frac { 1 }{ 2 }\) = \(\frac { 1 }{ 2 }\) > 0
⇒ (b, c) ∈ R.
But 1 + ac – 1 + (-8) (\(\frac { 1 }{ 2 }\) )
= 1 – 4 = -3 < 0
⇒ (a, c) ∉ R.
Thus, R is not transitive.
Hence, R is reflexive, symmetric but not transitive.

Question 6.
Let T be the set of all triangles in a plane with R, a relation in T given by :
R = {(T₁, T₂): T₁ is congruent to T₂}.
Show that R is an equivalence relation. (N.C.E.R.T.)
Solution:
We have:
R = {(T₁, T₂): T₁ is congruent to T₂}.
Now (T₁, T₂) ∈ R.
[ ∵ Every triangle is congruent to itself]
Thus R is reflexive.
(T₁, T₂) ∈ R
⇒ T₁ is congruent to T₂
⇒ T₂ is congruent to T₁
(T₂, T₁) ∈ R.
Thus R is symmetric.

(T₁, T₂) ∈ R and (T₂, T₃) ∈ R
⇒ T₁ is congruent to T₂ and T₂ is congruent to T₃
⇒ T₁ is congruent to T₃
(T₁, T₃) ∈ R.
Thus R is transitive.
Hence, R is an equivalence relation.

Question 7.
If R₁, and R₂ are equivalence relations in a set A, show that R₁ ∩ R₂ is also an equivalence relation. (N.C.E.R.T.)
Solution:
Since R₁ and R₂ are equivalence relations, [Given]
∴ (a, a) ∈ R₁
and (a, a) ∈ R₂ ∀ a ∈ A
⇒ (a, a) ∈ R₁ ∩ R₂ ∀ ∈ G
Thus R₁ ∩ R₂ is reflexive.
Now (a, b) ∈ R₁ ∩ R₂
⇒ (a, b) ∈ R₁
and (a, b) ∈ R₂
⇒ (b, a) ∈ R₁
and (b, a) ∈ R₂
⇒ (b, a) ∈ R₁ ∩ R₂

Thus R₁ n R2 is symmetric.
And (a, b) ∈ R₁ ∩ R₂
and (b, c) ∈ R₁ ∩ R₂
⇒ (a, c) ∈ R₁
and (a, c) ∈ R₂
⇒ (a, c) ∈ R₁ ∩ R₂
Thus R₁ ∩ R₂ is transitive.
Hence, R₁ ∩ R₂ is an equivalence relation.

Question 8.
Show that f: R-{2} → R -{1} defined by:
f(x) = \(\frac{x}{x-2}\) is one-one.
Also, if g : R -{1} → R -{2} as g{x) = \(\frac{2 x}{x-1}\) find gof.
Solution:
We have: f(x) = \(\frac{x}{x-2}\) and g(x) = \(\frac{2 x}{x-1}\)

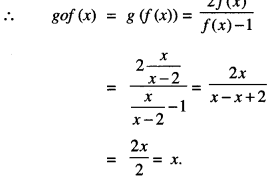
Question 9.
Let f: N → N be a function defined as :
f(x) – 9x² + 6x – 5.
Show that f: N → S, where S is the range of f, is invertible. Find the inverse of f and hence find f^-1 (43) and f^-1 (163).   (C.B.S.E. 2016)
Solution:
We have : f : N → S,
fix) = 9x² + 6x – 5.
Now f(x₁) = f(x₂)
⇒ 9x₁² + 6x₁ – 5 = 9 x₂² + 6x₂ – 5
⇒ 9(x₁² – x₂²) + 6 (x₁ – x₂) = 0
⇒ (x₁ – x₂) [9x₁ + 9x₂+ 6] = 0
⇒ x₁ = x₂ [x₁, x₂ ∈ N ]
⇒ f is one-one.
Let y ∈ S be an arbitrary number.
Now y = f(x)
⇒ y = 9x²+ 6x – 5
⇒ y = (3x + 1)² – 6
⇒ \(\sqrt{y+6}\) = 3x + 1
⇒ x = \(\frac{\sqrt{y+6}-1}{3}\) ∈ N
⇒ x = f^-1 (y).

Since f is one-one and onto
⇒ f is invertible.

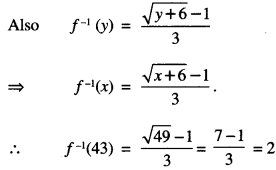
Question 10.
Let f: A → B be a function defined as f(x) = \(\frac{2 x+3}{x-3}\) where A = R – {3} and B = R – {2}.
Is the function ‘f ’one-one and onto ?
Is ‘f’ invertible? If yes, then find its inverse.
Solution:
Let x₁, x₂ ∈ A = R – {3}.
Now, f(x₁) = f(x₂)
⇒ \(\frac{2 x_{1}+3}{x_{1}-3}=\frac{2 x_{2}+3}{x_{2}-3}\)
⇒ (2x₁ + 3) (x₂– 3) = (2x₂ + 3) (x₁ – 3)
⇒ 2x₁x₂ – 6x₁ + 3x₂ – 9 = 2x₁ x₂ – 6x₂ + 3x₁ – 9
⇒ – 6x₁ + 3x₂ = – 6x₂ + 3x₁
⇒ 9x₁ = 9x₂
⇒ x₁ = x₂
Thus, ‘f’ is one-one.
Let y ∈ R- {2}.
Let y = f(x₀).
Then \(\frac{2 x_{0}+3}{x_{0}-3}\) = y
⇒ 2x₀ + 3 = x₀y – 3y
⇒ x₀(y – 2) = 3(y + 1)
⇒ x₀ = \(\frac{3(y+1)}{y-2}\)
Now , y ∈ R – {2 } ⇒ \(\frac{2 x_{0}+3}{x_{0}-3}\) ∈ R – {2}

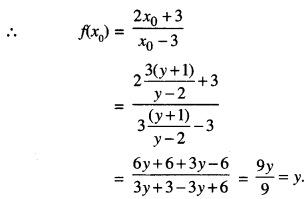
Thus, ‘f’ is onto.
Hence, ‘f’ is one-one onto and consequently ‘f’ is invertible.
Also y = \(\frac{2 x+3}{x-3}\)
xy – 3y = 2x + 3
x(y- 2) = 3(y +1)
x = \(\frac{3(y+1)}{y-2}\)
f^-1 (y) = \(\frac{3(y+1)}{y-2}\)
Hence, f^-1 (x) = \(\frac{3(x+1)}{x-2}\) for all x ∈ R – {2}.

Question 11.
Let A = R – {2} and B = R – {1}. If f: A → B is a function defined by :
f(x) = \(\frac{x-1}{x-2}\) Show that f is one one and onto.
Hence, find f^-1.
Solution:
(i) One-one : Let x₁ x₂ ∈ R – {2} such that
f(x₁) = f(x₂)
⇒ \(\frac{x_{1}-1}{x_{1}-2}=\frac{x_{2}-1}{x_{2}-2}\)
⇒ x₁x₂ – 2x₁ – x₂ + 2 = x₁x₂ – 2x₂ – x₁ + 2
⇒ x₁ = x₂
Thus,f one-one.

Onto : Let f(x) = y.
Thus \(\frac{x-1}{x-2}\) = y ⇒ x = \(\frac{2 y-1}{y-1}\)
∴ Range of f = R – {1}
= Co-domain of B
Thus f is onto.

(ii) f^-1(y) = \(\frac{2 y-1}{y-1}\)
Hence f^-1(x) = \(\frac{2 x-1}{x-1}\)

Question 12.
Show that the relation S on the set:
A = {x ∈ Z : 0 ≤ x ≤ 12} given by S = {(a, b) :a,b e Z, |a – b| is divisible by 3} is an equivalence relation.
Solution:
Reflexive :
(a, a) ∈ S
⇒ |a – a| i.e., | 0 | is divisible by 3.
Thus, S is reflexive.

Symmetric:
(a, b) ∈ S ⇒ | a – b | is divisible by 3
⇒ |b – a| is divisible by 3
⇒ (b, a) ∈ S.
Thus, S is symmetric.

Transitive :
Let (a, b) ∈ S and (b, c) ∈ S.
Thus |a – b| = 3m and |b – c| = 3n
⇒ a – b = ± 3m and b – c = ± 3 n.
∴ (a – c) = 3(± m ± n)
⇒ a – c is divisible by 3
⇒ | a – c | is divisible by 3
⇒ (a, c) ∈ S.
Thus, S is transitive.
Hence, S is an equivalence relation.

Relations and Functions Important Extra Questions Long Answer Type 2

Question 1.
Let A = (1,2,3,…, 9} and R be the relation in A x A defined by (a, b) R (c, d) if: a + d = b + c for (a, b), (c, d) in A x A.
Prove that R is an equivalence relation. Also obtain the equivalence class {(2,5)}.   (C.B.S.E. 2014)
Solution:
(i) We have : (a, b) R (c, d)
⇒ a + d = b + c on the set A = {1, 2, 3,…, 9}.
(a) (a, b) R (a, b)
⇒ a + b = b + a, which is true.
[∵ a + b = b + a ∀ a, b ∈ A]
Thus R is reflexive.

(b) (a, b) R (c, d)
⇒ a + d = b + c
(c, d) R (a, b)
⇒ c + b = d + a.
But c + b = b + c
and d + a = a + d ∀ a, b, c, d ∈ A.
∴ (a, b) R(c, d) = (c, d) R (a, b).
Thus R is symmetric.

(c) (a,b)R(c,d)
⇒ a + d = b + c ∀ a, b, c, d ∈ A ……..(1)
(c,d)R(e,f)
⇒ c + f = d + e ∀ c, d, e,f ∀ A ……………. (2)

∴ Adding (1) and (2),
(a + d) + (c +f) = (b + c) + (d + e)
⇒ a + f = b + e
⇒ (a, b) R (e, f).
Thus R is transitive.
Hence, the relation R is an equivalence relation.

(ii) {(2, 5)} = {(1, 4), (2, 5), (3, 6), (4, 7), (5, 8), (6, 9)}.
[∵ 2 + 4 = 5 + 1; etc.]

Question 2.
Let N denote the set of all natural numbers and R be the relation on N x N defined by : (a, b) R(c,d) is ad(b + c) = bc(a + d).
Show that R is an equivalence relation.    (C.B.S.E. 2015)
Solution:
We have : (a, b) R (c, d)
⇒ ad (b + c) = bc (a + d) on N.
(i) {a, b) R (a, b)
⇒ ab(b + a) = ba (a + b)
⇒ ab(a + b) = ab (a + ft),
which is true.
Thus R is reflexive.

(ii) (a, b) R (c, d)
⇒ ad(b + c) = be (a + d)
⇒ bc(a + d) = ad (b + c)
⇒ cb(d + a) = da (c + b)
[∵ bc = cb and a + d = d + a;
etc. ∀ a, b, c, d ∈ N]
⇒ (cb) R (a,b).
Thus R is symmetric

(iii) Let (a , b) R (c, d) and (c, d) R ( e, f)
∴ ad (b + c) = bc (a + d)
and cf(d + e) = de(c + f)


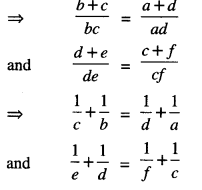
⇒  be(a+f) = af(b+e)
⇒  af(b+e) = be(a+f)
⇒  (a, b) R (e,f).
Thus R is transitive.
Hence, R is an equivalence relation.

Question 3.
Show that the relation in the set A = {x:x ∈ W, 0 ≤ x ≤ 12} given by R = {(a, b) : (a – b) is a multiple of 4} is an equivalence relation. Also find the set of all. elements related to 2.
Solution:
We have :
R = {(a, b): (a- b) is a multiple of 4},
where a, b ∈ A = {x: x ∈ W, 0 ≤ x ≤ 12}.
(a) For any a ∈ A, we have :
(a – a) = 0, which is a multiple of 4
⇒ (a, a) ∈ R ∀ a ∈ A.
Thus R is reflexive.

(b) Let a, b ∈ A.
Now (a, b) ∈ R
⇒ (a – b) is a multiple of 4
⇒ (b – a) is a multiple of 4
⇒ (b, a) ∈ R
Thus R is symmetric.

(c) Let a, b, c ∈ A.
Now (a, b) ∈ R
and (b, c) ∈ R
⇒ (a – b) is a multiple of 4 and (b – c) is a multiple of 4
⇒ (a – b) + (b – c) is a multiple of 4
⇒ (a – c) is a multiple of 4
⇒ (a, c) ∈ R.
Thus R is transitive.
Hence, R is an equivalence relation.

Question 4.
Let R be the relation defined in the set A = {1,2,3,4,5,6,7} by :
R = {(a, b) : both a and b are either odd or even}.
Show that R is an equivalence relation. Further, show that all the elements of the subset:
(1, 3, 5, 7} are related to each other and all the elements of the subset {2,4,6} are related to each other, but no element of the subset {1, 3, 5, 7} is related to any element of the subset {2,4,6}. (N.C.E.R.T.)
Solution:
We have:
R = {{a, b): both a, b are either odd or even}.
(i) Let a ∈ A.
Both a and a are either odd or even.
∴ (a, a) ∈ R.
Thus R is reflexive.

(ii) Let (a, b) ∈ R
⇒ both a and b are either odd or even
⇒ both b and a are either odd or even
⇒ (b, a) ∈ R.
Thus R is symmetric.

(iii) Let {a, b) ∈ R and (b, c) ∈ R.
∴ Both a, b and both b, c are either odd or even
⇒ both a, c are either odd or even
⇒ (a, c) ∈ R.
Thus R is transitive.
Hence, R is an equivalence relation.
Further all elements of {1,3,5,7} are related to each other.
[∵ All elements of this subset are odd] Similarly all elements of {2,4,6} are related to each other.
[∵All elements of this subset are even] But no element of {1, 3, 5, 7} is related to any element of {2, 4, 6}.
[∵Elements of {1, 3, 5, 7] are odd while elements of [2,4,6] are even]

Question 5.
Show that f : N → N given by :

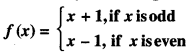
is both one-one and onto.   (A.I.C.B.S.E. 2012)
Solution:
One-One.
Here we discuss the following possible cases :
(i) When x₁ is odd and x₂ is even.
Here f(x₁) = f(x₂)
⇒ x₁ + 1 = x₂ – 1
⇒ x₂ = x₁ = 2, which is impossible.

(ii) When x₁ is even and x₂ is odd.
Here f(x₁) =f(x₂)
⇒ x₁ – 1 = x₂ + 1
⇒ x₁ – x₁ = 2, which is impossible.

(iii) When x₁ and x₂ are both odd.
Here f(x₁) = f(x₂)
⇒ x₁ + 1 = x₂ + 1
⇒ x₁ = x₂
∴ ‘f’ is one-one.

(iv) When x₁ and x₂ are both even.
Here f(x₁) = f(x₂)
⇒ x₁ – 1 = x₂ – 1
⇒ x₁ = x₂
∴ ‘ f’ is one-one.

Onto. Let ‘x’ be an arbitrary natural number. When x is an odd natural number, then there exists an even natural number (x + 1) such that: f(x + 1) = (x + 1) – 1 = x.
When x is an even natural number, then there exists an odd natural number (x – 1) such that:
f(x – 1) = (x – 1) + 1 = x.
∴ Each x ∈ N has its pre-image in N.
Thus ‘f ’ is onto.
Hence, ‘f ’ is both one-one and onto.

Question 6.
Show that the function f : R → R defined by:
\(\frac{x}{x^{2}+1}\) ∀ x ∈ R is neither one-one nor onto. Also, if g : R → R is defined g(x) = 2x -1, find fog (x). (C.B.S.E. 2018)
Solution:
We have : f(x) = \(\frac{x}{x^{2}+1}\)
(i) One-one, f(x₁) = f(x₂)
⇒ \(\frac{x_{1}}{x_{1}^{2}+1}=\frac{x_{2}}{x_{2}^{2}+1}\)
⇒ x₁x₂² + x₁ = x₂x₁² + x₂
⇒  x₁x₂ (x₂ – x₁) = x₂ – x₁
x₁x₂ = 1
x₁ = \(\frac{1}{x_{2}}\)
x₁ ≠ x₂
Thus, f is not one-one.

Onto:
⇒ f(x) = y
⇒ \(\frac{x}{x^{2}+1}\) = y
⇒ x = yx² + y
⇒ x²y + y – x = 0
⇒ x can not be expressed in y.
Thus, f is not onto.
Hence, f is neither one-one nor onto.

(ii) Since g (x) = 2x – 1,
∴ fog (x) = f(g (x)) = f(2x – 1)
= \(\frac{2 x-1}{(2 x-1)^{2}+1}=\frac{2 x-1}{4 x^{2}-4 x+2}\)

Question 7.
Show that the relation R on the set Z of all integers defined by (x, y) ∈ R ⇔ (x – y) is divisible by 3 is an equivalence relation.
(C.B.S.E. 2018 C)
Solution:
(x – x) = 0 is divisible by 3 for all x ∈ Z.
So, (x, x) ∈ R
:. R is reflexive.
(x – y) is divisibile by 3 implies (y – x) is divisible by 3.
So (x, y) ∈ R implies (y – x) ∈ R, x. y ∈ Z
⇒ R is symmetric.
(x – y) is divisibile by 3 and (y – z) is divisible by 3.
So (x – z) = (x – y) + (y + z) is divisible by 3.
∴ (x, z) ∈ R ⇒ R is transitive.
Hence, R is an equivalence relation.

Question 8.
Let A = R – {3} and B = R – {1}. Consider the function f: A → B defined by:
f(x) = [latyex]=\left(\frac{x-2}{x-3}\right)[/latex]. Show that ‘f’ is one-one and onto and hence find f^-1. (C.B.S.E. 2012)
Solution:
Let x₁, x₂ ∈ R-{3}.
Now f(x₁) = f(x₂)
⇒ \(\frac{x_{1}-2}{x_{1}-3}=\frac{x_{2}-2}{x_{2}-3}\)
⇒ (x₁ – 2) (x₂ – 3) = (x₁ – 3) (x₂ – 2)
⇒ x₁x₂ – 3x₁ – 2x₂ + 6 = ⇒ x₁x₂ – 2x₁ – 3x₂ + 6
⇒ x₁ = x₂
Thus ‘f’ is one-one.
Let y ∈ R – {1}.
Let y = f(x₀).
Then \(\frac{x_{0}-2}{x_{0}-3}\) = y
x₀ – 2 = x₀y – 3y
x₀(y-1) = 3y – 2
x₀ = \(\frac{3 y-2}{y-1}\)
Now y ∈ R – {1}.

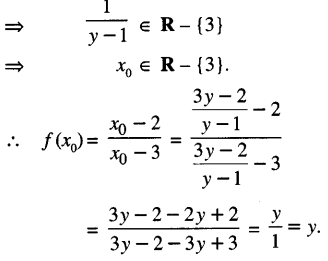
Thus ‘f’ is onto.
Hence, ‘f’ is one-one and onto function
⇒ ‘f’ is invertible.
Also y = \(\frac{x-2}{x-3}\)
⇒ xy — 3y = x – 2
⇒ x (y — 1) = 3y – 2
x = \(\frac{3y-2}{y-1}\)
f^-1 (y) = \(\frac{3 y-2}{y-1}\)
Hence, f^-1 (x) = \(\frac{3 x-2}{x-1}\)– for all x ∈ R-{1}.

Question 9.
Let Y = {n²: n ∈ N} ⊂ N. Consider f : N → Y as f(n) = n². Show that if is invertible. Find the inverse of ‘f.   (N.C.E.R.T.)
Solution:
Let y ∈ Y, where y is arbitrary.
Here y is of the form n², for n∈ N
⇒  n = √y.
This motivates a function :
g : Y → N, defined by g (y) = √y .

Now gof(n ) = g (f(n)) = g (n²) = √n²= n
and fog (y) =f(g (y))
= f (√y) = (√y)² = y
Thus gof = I_N
and fog = I_Y.
Hence, ‘ f ’ is invertible with f^-1 = g.

Question 10.
Let f : W → W be defined by:

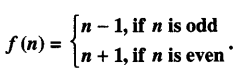
Show that ‘f ’ is invertible. Find the inverse of ‘f ’. (Here ‘ W’ is the set of whole numbers) (A.I.C.B.S.E. 2015)
Solution:
We have : f : W → W defined by :

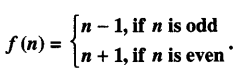
f is one-one.
When n₁ and n₂ are both odd,
then f(n₁) = f(n₂)
⇒ n₁ – 1 = n₂ – 1
⇒ n₁ = n₂
When n₁ and n₂ are both even, then
f(n₁) = f(n₂)
⇒ n₁ + 1 = n₂ + 1
⇒ n₁= n₂

∴ In both cases,
f(n₁) = f(n₂)
⇒ n₁ = n₂
When n₁is odd and n₂ is even,
then f(n₁) =  n₁ – 1, which is even
and f(n₂) = n₂ + 1, which is odd.
∴ (n₁) ≠ (n₂)
⇒ f(n₁) ≠ f(n₂)
Similarly when n₁ is even and n₂ is odd,
∴ (n₁) ≠ (n₂)
⇒ f(n₁) ≠ f(n₂)
In each case, ‘f’ is one-one.

f is onto.
When n is odd whole number, then there exists an even whole number
n – 1 ∈ W such that
f(n- 1) = (n -1) + 1 = n.
When n is even whole number, then there exists an odd whole number n + 1 ∈ W such that
f(n +1) = (n + 1) -1 = n.
Also f(1) = 0 ∈ W.
∴ each number of W has its pre-image in W.
Thus f ’ is onto.
Hence, ‘f’ is one-one onto
⇒ ‘f’ is invertible.
To obtain f^-1.
Let n₁, n₂ ∈ W
such that f(n₁) = f(n₂)
n₁ + 1 = n₂, if n₁ is even
n₁ – 1 = n₂, if n₁ is odd.

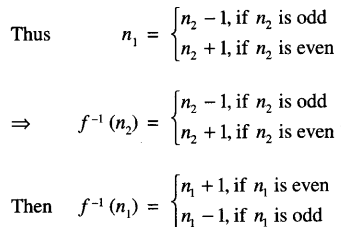
Hence f = f^-1