Vectors Class 12 Important Extra Questions Maths Chapter 10

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 10 Vectors. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 10 Important Extra Questions Vectors

Vectors Important Extra Questions Very Short Answer Type

Question 1.
Classify the following measures as scalar and vector quantities:
(i) 40°
(ii) 50 watt
(iii) 10gm/cm³
(iv) 20 m/sec towards north
(v) 5 seconds. (N.C.E.R.T.)
Solution:
(i) Angle-scalar
(ii) Power-scalar
(iii) Density-scalar
(iv) Velocity-vector
(v) Time-scalar.

Question 2.
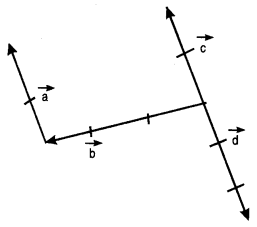
In the figure, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Co-initial. (N.C.E.R.T.)

Solution:
(i) \(\vec{a}, \vec{c}\) and \(\vec{a}\) are collinear vectors.
(ii) \(\vec{a}\) and \(\vec{c}\) are equal vectors.
(iii) \(\vec{b}\), \(\vec{c}\) and \(\vec{d}\) are co-initial vectors.

Question 3.
Find the sum of the vectors:
\(\vec{a}\) = \(\hat{i}-2 \hat{j}+\hat{k}\), \(\vec{a}\) = \(-2 \hat{i}+4 \vec{j}+5 \hat{k}\) and \(\vec{c}\) = \(\hat{i}-6 \hat{j}-7 \hat{k}\). (C.B.S.E. 2012)
Solution:
Sum of the vectors = \(\hat{a}+\hat{b}+\hat{c}\)

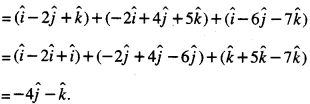
Question 4.
Find the vector joining the points P (2,3,0) and Q (-1, – 2, – 4) directed from P to Q. (N.C.E.R.T.)
Solution:
Since the vector is directed from P to Q,
∴ P is the initial point and Q is the terminal point.
∴ Reqd. vector = \(\overrightarrow{\mathrm{PQ}}\)

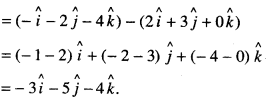
Question 5.
If \(\vec{a}=x \hat{i}+2 \hat{j}-z \hat{k}\) and \(\vec{b}=3 \hat{i}-y \hat{j}+\hat{k}\) are two equal vectors, then write the value of x + y + z. (C.B.S.E. 2013)
Solution:
Here
\(\vec{a}=\vec{b} \Rightarrow x \hat{i}+2 \hat{j}-z \hat{k}=3 \hat{i}-y \hat{j}+\hat{k}\)
Comparing,A: = 3,2 = -y i.e.y = -2,~z= 1 i.e. z = -1.
Hence, x + y + z = 3 – 2 – 1 = 0.

Question 6.
Find the unit vector in the direction of the sum of the vectors:
\(\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}\) and \(\vec{b}=-\hat{i}+\hat{j}+3 \hat{k}\) (N.C.E.R.T.)
Solution:

Question 7.
Find the value of ‘p’ for which the vectors : \(3 \hat{i}+2 \hat{j}+9 \hat{k}\) and \(\hat{i}-2 p \hat{j}+3 \hat{k}\) are parallel. (A.I.C.B.S.E. 2014)
Solution:
The given vectors \(3 \hat{i}+2 \hat{j}+9 \hat{k}\) and \(\hat{i}-2 p \hat{j}+3 \hat{k}\) are parallel
If \(\frac{3}{1}=\frac{2}{-2 p}=\frac{9}{3}\) if 3 = \(\frac{1}{-p}\) = 3
if p = \(-\frac{1}{3}\)

Question 8.
If \(\vec{a}\) and \(\vec{b}\) are perpendicular vectors, \(|\vec{a}+\vec{b}|\) = 13 and \(|\vec{a}|\) =5, find the value of \(|\vec{b}|\) (A.I.C.B.S.E. 2014)
Solution:

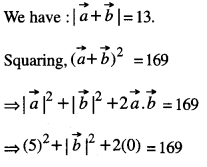
[∵ \(\vec{a}\) and \(\vec{b}\) are perpendicular ⇒ \(\vec{a}\) \(\vec{b}\) = 0 ]

⇒ \(|\vec{b}|^{2}\) = 169 – 25 = 144.
Hence, \(|\vec{b}|\) = 12.

Question 9.
Find the magnitude of each of the two vectors \(\vec{a}\) and \(\vec{b}\) , having the same magnitude such that the angle between them is 60° and their scalar product is \(\frac { 9 }{ 2 }\) (C.B.S.E. 2018)
Solution:
By the question, \(|\vec{a}|=|\vec{b}|\) …(1)
Now \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\) cos θ
⇒ \(\frac { 9 }{ 2 }\) = \(|\vec{a}||\vec{a}|\) cos 60° [Using (1)]
⇒ \(\frac{9}{2}=|\vec{a}|^{2}\left(\frac{1}{2}\right)\)
⇒ \(|\vec{a}|^{2}\) = 9.
Hence, \(|\vec{a}|=|\vec{b}|\) = 3.

Question 10.
Find the area of the parallelogram whose diagonals are represented by the vectors: \(\vec{a}=2 \hat{i}-3 \hat{j}+4 \hat{k}\) and \(\vec{b}=2 \hat{i}-\hat{j}+2 \hat{k}\) (C.B.S.E. Sample Paper 2018-19)
Solution:

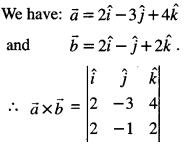
= \(\hat{i}\)(-6 + 4) – \(\hat{j}\)(4 – 8) + \(\hat{k}\)( – 2 + 6)
= – 2\(\hat{i}\) + 4\(\hat{j}\) + 4\(\hat{k}\).
∴ \(|\vec{a} \times \vec{b}|=\sqrt{4+16+16}=\sqrt{36}\)= 6.
∴ Area of the parallelogram = \(\frac{1}{2}|\vec{a} \times \vec{b}|\)
= \(\frac{1}{2}\) (6) = 3 sq. units.

Question 11.
Find the angle between the vectors: \(\vec{a}=\hat{i}+\hat{j}-\hat{k}\) and \(\vec{b}=\hat{i}-\hat{j}+\hat{k}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
We have:\(\vec{a}=\hat{i}+\hat{j}-\hat{k}\) and \(\vec{b}=\hat{i}-\hat{j}+\hat{k}\)
If ‘θ’ be the angle between \(\vec{a}\) and \(\vec{b}\)

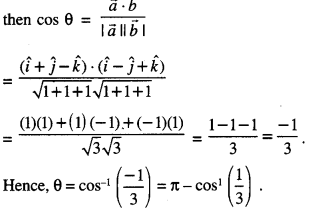
Question 12.
Find \(\vec{a} \cdot(\vec{b} \times \vec{c})\), if : \(\vec{a}=2 \hat{i}+\hat{j}+3 \hat{k}, \vec{b}=-\hat{i}+2 \hat{j}+\hat{k}\), and \(\vec{c}=3 \hat{i}+\hat{j}+2 \hat{k}\) (A.I.C.B.S.E. 2014)
Solution:
We have:

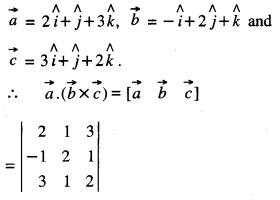
= 2 (4 – 1) – (1) (-2 – 3) + 3 (-1 – 6)
= 6 + 5-21 = 11 – 21 = -10.

Vectors Important Extra Questions Short Answer Type

Question 1.
If θ is the angle between two vectors:
\(\hat{i}-2 \hat{j}+3 \hat{k}\) and \(3 \hat{i}-2 \hat{j}+\hat{k}\) ,find sinθ.   (C.B.S.E. 2018)
Solution:

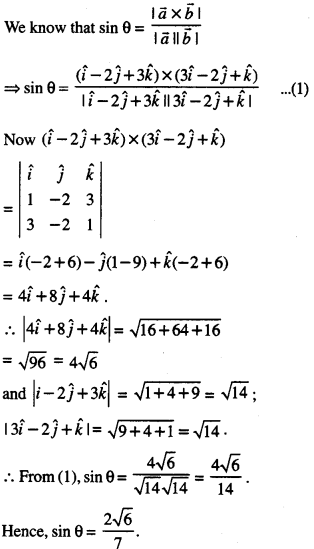
Question 2.
X and Y are two points with position vectors \(\overrightarrow{3 a}+\vec{b}\) and \(\vec{a}-3 \vec{b}\) respectively. Write the po-sition vector of a point Z which divides the line segment XY in the ratio 2:1 externally. (C.B.S.E. Outside Delhi 2019)
Solution:
Position vector of
A = \(\frac{2(\vec{a}-3 \vec{b})-(3 \vec{a}+\vec{b})}{2-1}\) = \(-\vec{a}-7 \vec{b}\)

Question 3.
Find the unit vector perpendicular to both \(\overrightarrow{a}\) and \(\overrightarrow{b}\), where:
\(\vec{a}=4 \hat{i}-\hat{j}+8 \hat{k}\) and \(\vec{b}=-\hat{j}+\hat{k}\)
(C.B.S.E. 2019 C)
Solution:

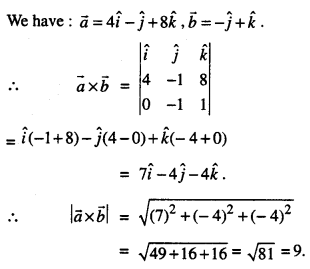
Hence, the unit vector perpendicular to both \(\vec{a}\) and \(\vec{b}\)

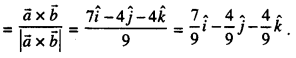
Question 4.
If \(\vec{a}=2 \hat{i}+2 \hat{j}+\hat{k}\) , \(\vec{b}=-\hat{i}+{2} \hat{j}+\hat{k}\) and \(\vec{c}=3 \hat{i}+\hat{j}\) are such that \(\vec{a}+\lambda \vec{b}\) is perpendicular to \(\vec{c}\), then find the value of λ . (C.B.S.E. 2019 C)
Solution:
We have:
a = \(\vec{a}=2 \hat{i}+2 \hat{j}+\hat{k}\) and \(\vec{b}=-\hat{i}+{2} \hat{j}+\hat{k}\)
∴ \(\vec{a}+\lambda \vec{b}=(2 \hat{i}+2 \hat{j}+3 \hat{k})+\lambda(-\hat{i}+2 \hat{j}+\hat{k})\)
= (2 – λ)\(\hat{i}\)+(2 + 2λ)\(\hat{j}\) + (3+λ)\(\hat{k}\).
Now, (\(\vec{a}+\lambda \vec{b}\)) is perpendicular to c ,
∴ \((\vec{a}+\lambda \vec{b}) \cdot \vec{c}=0\)
⇒ ((2 – λ) \(\hat{i}\) + (2 + 2λ)\(\hat{j}\) + (3 + λ\(\hat{k}\)). (3\(\hat{i}\) + \(\hat{j}\)) = 0
⇒ (2 – λ)(3) + (2 + 2λ) (1) + (3 + λ)(0) = 0
⇒ 6 – 3λ + 2 + 2λ = 0
⇒ -λ, + 8 =0.
Hence, λ,=8.

Question 5.
Let \(\vec{a}=\hat{i}+2 \hat{j}-3 \hat{k}\) and \(\vec{b}=3 \hat{i}-\hat{j}+2 \hat{k}\) be two vectors. Show that the vectors (\(\vec{a}+\vec{b}\)) and
(\(\vec{a}-\vec{b}\)) are perpendicular to each other. (C.B.S.E. Outside Delhi 2019)
Solution:
Here, \(\vec{a}+\vec{b}\) = (\(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\)) + (3\(\hat{i}\) – \(\hat{j}\) + 2\(\hat{k}\))
= 4\(\hat{i}\) + \(\hat{j}\) –\(\hat{k}\)
and \(\vec{a}-\vec{b}\) = (\(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\)) – (3\(\hat{i}\) – j + 2k)
= -2\(\hat{i}\) + 3\(\hat{j}\) – 5\(\hat{k}\).
Now
\(\vec{a}+\vec{b}\) . \(\vec{a}-\vec{b}\) = (4\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\))- (-2\(\hat{i}\) + 3 \(\hat{j}\) – 5\(\hat{k}\))
= (4) (- 2) + (1) (3)+(-1) (- 5)
= – 8 + 3 + 5 = 0.
Hence \(\vec{a}+\vec{b}\) is perpendicular to \(\vec{a}-\vec{b}\).

Question 6.
If the sum of two unit vectors is a unit vector, prove that the magnitude of their difference
is √3 . (C.B.S.E. 2019)
Solution:

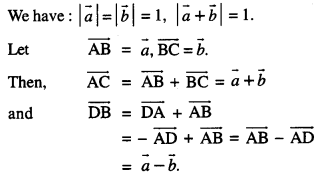
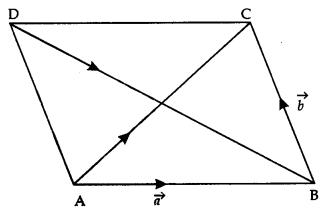
By the question,
\(|\overrightarrow{\mathrm{AB}}|=|\overrightarrow{\mathbf{B C}}|=|\overrightarrow{\mathrm{AC}}|=1\)
⇒ ΔABC is equilateral, each of its angles be¬ing 60°
⇒ ∠DAB = 2 x 60° = 120° and ∠ADB = 30°.
By Sine Formula,
\(\frac{\mathrm{DB}}{\sin \angle \mathrm{DAB}}=\frac{\mathrm{AB}}{\sin \angle \mathrm{ADB}}\)

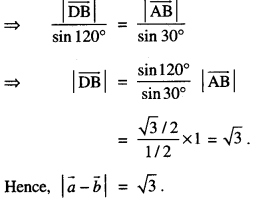
Question 7.
If \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) and \(|\vec{a}|\) = 3, \(|\vec{b}|\) = 5 and \(|\vec{a}|\) = 7, then find the value of \(\overrightarrow{a} \cdot \overrightarrow{b}+\overrightarrow{b} \cdot \overrightarrow{c}+\overrightarrow{c} \cdot \overrightarrow{a}\)
(C.B.S.E. Sample Paper 2019-20)
Solution:

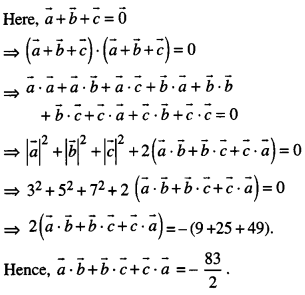
Question 8.
Find \(|\vec{a}-\vec{b}|\), if two vectors a and b are such that \(|\vec{a}|\) = 2,\(|\vec{b}|\) = 3 and \(\vec{a} \cdot \vec{b}\) = 4. (N.C.E.R.T.)
Solution:

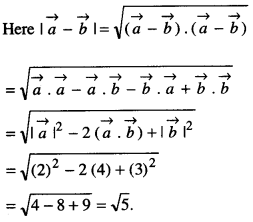
Question 9.
Find the work done by the force \(\overrightarrow{\mathbf{F}}=2 \hat{i}+\hat{j}+\hat{k}\) acting on a particle, if the particle is displaced from the point with position vector \(2 \hat{i}+\hat{j}+2 \hat{k}\) to the point with position vector \(3 \hat{i}+4 \hat{j}+5 \hat{k}\)
Solution:
Here F = 2 \(\hat{i} \)+ \(\hat{j} \) + \(\hat{k} \)
and d = (3 \(\hat{i} \) + 4\(\hat{j} \) + 5k) – (2 \(\hat{i} \) + 2\(\hat{j} \) + 2\(\hat{k} \) )
– \(\hat{i} \) +2\(\hat{j} \) + 3\(\hat{k} \) .
∴ Work done = \(\overrightarrow{\mathrm{F}} \cdot \vec{d}\)
= (2 \(\hat{i} \) + \(\hat{j} \) + \(\hat{k} \) ). ( \(\hat{i} \) + 2\(\hat{j} \) + 3\(\hat{k} \) )
= (2) (1) + (1) (2) + (1) (3)
= 2 + 2 + 3
= 7 units.

Question 10.
Find ‘λ’ if
(2\(\hat{i} \) + 6\(\hat{j} \) + 14\(\hat{k} \)) x (\(\hat{i} \) – λ\(\hat{j} \) + 7\(\hat{k} \)) = 0. (A.I.C.B.S.E. 2010)
Solution:
We have:
(2\(\hat{i}\) + 6\(\hat{j}\) + 14\(\hat{k}\)) x (\(\hat{i}\) – λ\(\hat{j}\) + 7\(\hat{k} \)) = 0
⇒ \(\hat{i} \) (42 + 14λ) – \(\hat{j}\)(14-14) + \(\hat{k}\) (-2λ – 6) = 0
⇒ 14\(\hat{i} \)(λ + 3)-2(λ + 3) ifc = o
= λ+3 = 0.
Hence, λ = -3.

Question 11.
If \(\vec{a}\) and \(\vec{b}\) are two vectors such that \(|\vec{a} \cdot \vec{b}|\)
=\(|\vec{a} \times \vec{b}|\), then what is the angle between \(\vec{a}\) and b ? (A.I.C.B.S.E. 2010)
Solution:
We have \(|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|\)
⇒ \(|\vec{a}||\vec{b}| \cos \theta=|\vec{a}||\vec{b}| \sin \theta\)
⇒ cos θ = sin θ ⇒ tan θ = 1 ⇒ θ = 45°.
Hence, the angle between \(\vec{a}\) and \(\vec{a}\) = 45°.

Question 12.
If \(\vec{a}=2 \hat{i}+3 \hat{j}+\hat{k}\), b = \(\vec{b}=\hat{i}-2 \hat{j}+\hat{k}\) and \(\vec{c}=-3 \hat{i}+\hat{j}+2 \hat{k}\) ,find \([\vec{a} \vec{b} \vec{c}]\).   (C.B.S.E. 2019)
Solution:
We have : \(\vec{a}\) = 2\(\hat{i}\) + 3\(\hat{j}\) + \(\hat{k}\), \(\vec{b}\) = \(\hat{i}\) – 2\(\hat{j}\) + \(\hat{k}\) and \(\vec{c}\) = – 3\(\hat{i}\) + \(\hat{j}\) + 2\(\hat{k}\)
∴ \([\vec{a} \vec{b} \vec{c}]=\left|\begin{array}{rrr}
2 & 3 & 1 \\
1 & -2 & 1 \\
-3 & 1 & 2
\end{array}\right|\)
= 2 (-4-1)-3(2 + 3)+ 1.(1 -6)
= 2(-5)-3(5)+ 1(-5)
= -10-15-5 = -30.

Question 13.
For three non-zero vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\), prove that \([\vec{a}-\vec{b}, \vec{b}-\vec{c}, \vec{c}-\vec{a}]\) = 0. (C.B.S.E. 2019)
Solution:

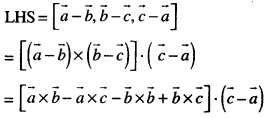
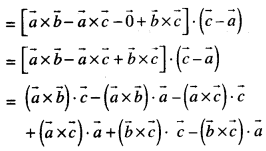
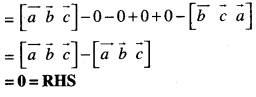
Vectors Important Extra Questions Long Answer Type

Question 1.
Let \(\vec{a}=4 \hat{i}+5 \hat{j}-\hat{k}\) and \(\vec{b}=\hat{i}-4 \hat{j}+5 \hat{k}\) and \(\vec{c}=3 \hat{i}+\hat{j}-\hat{k}\). Find a vector \(\vec{a}\) which is perpendicular to both \(\vec{c}\) and \(\vec{b}\) and
\(\vec{d} \cdot \vec{a}\) =21. (C.B.S.E. 2018)
Solution:
Wehave: \(\vec{a}\) = 4\(\hat{i}\) + 5\(\hat{j}\) – \(\hat{k}\)
\(\vec{b}\) = \(\hat{i}\) – 4\(\hat{j}\) + 5\(\hat{k}\) and
\(\vec{c}\) = 3\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\)
Let \(\vec{d}\) = x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)

since \(\vec{d}\) is perpendicular to both \(\vec{c}\) and \(\vec{b}\)
\(\vec{d} \cdot \vec{c}\) = 0 and \(\vec{d} \cdot \vec{b}\) = 0
⇒ (x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)) . (3\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\)) = 0

and (x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)) . (\(\hat{i}\) -4\(\hat{j}\)+5\(\hat{j}\)) = 0
⇒ 3x + y-z = 0 …(1)
and x-4y + 5z = 0 …(2)
Also, \(\vec{d} \cdot \vec{a}\) = 21
⇒ (x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)). (4\(\hat{i}\) + 5\(\hat{j}\) – \(\hat{k}\)) =21
⇒ 4x + 5y-z = 21 …(3)
Multiplying (1) by 5,
1 5x + 5y – 5z = 0 …(4)
Adding (2) and (4),
16x + y = 0 …(5)
Subtracting (1) from (3),
x + 4y = 21 …(6)
From (5),
y = -16x …(7)
Putting in (6),
x – 64x = 21
-63x: = 21
Putting in (7), y = \(-16\left(-\frac{1}{3}\right)=\frac{16}{3}\)
Putting in (1), \(3\left(-\frac{1}{3}\right)+\frac{16}{3}\) – z = 0
z = 13/3
Hence \(\vec{d}=-\frac{1}{3} \hat{i}+\frac{16}{3} \hat{j}+\frac{13}{3} \hat{k}\)

Question 2.
If \(\vec{p}=\hat{i}+\hat{j}+\hat{k}\) and \(\vec{q}=\hat{i}-2 \hat{j}+\hat{k}\) ,find a vector of magnitude 5√3 units perpendicular to the vector \(\vec{q}\). and coplanar with vector \(\vec{p}\) and \(\vec{q}\). (C.B.S.E. 2018)
Solution:
Let \(\vec{r}=a \hat{i}+b \hat{j}+c \hat{k}\) be the vector.
Since \(\vec{r} \perp \vec{q}\)
(1) (a) + (-2) (b) + 1 (c) = 0
⇒ a – 2b + c = 0
Again, \(\vec{p}\) , \(\vec{q}\) and \(\vec{r}\) and coplanar,

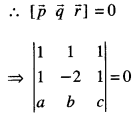
⇒ (1) (-2c – b) – (1) (c – a) + (1) (b + 2a) = 0
⇒ -2c-b-c + a + b + 2a = 0
⇒ 3a – 3c = 0
⇒ a – c – 0
Solving (1) and (2),

Question 3.
If \(\hat{i}+\hat{j}+\hat{k}, \quad 2 \hat{i}+5 \hat{j}, \quad 3 \hat{i}+2 \hat{j}-3 \hat{k}\) and \(\hat{i}-6 \hat{j}-\hat{k}\) respectively are the position vectors of points A, B, C and D, then find the angle between the straight lines AB and CD. Find
whether \(\overrightarrow{\mathbf{A B}}\) and \(\overrightarrow{\mathbf{CD}}\) arecollinearornot
(C.B.S.E. 2019)
Solution:
Note : If ‘θ’ is the angle between AB and CD,
then θ is also the angle between \(\overrightarrow{\mathbf{A B}}\) and \(\overrightarrow{\mathbf{C D}}\) .
Now \(\overrightarrow{\mathbf{A B}}\) = Position vector of B – Position vector of A

Since 0 ≤ θ ≤ π, it follows that θ = π. This shows that \(\overrightarrow{\mathbf{A B}}\) and \(\overrightarrow{\mathbf{C D}}\) are collinear.
Alternatively, \(\overrightarrow{\mathrm{AB}}=-\frac{1}{2} \overrightarrow{\mathrm{CD}}\) which implies
that \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{\mathrm{CD}}\) are collinear vectors.

Question 4.
If \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) and \(|\vec{a}|\) = 3, \(|\vec{b}|\) = 5, and \(|\vec{c}|\) =7, find the angle between \(\vec{a}\) and \(\vec{b}\) . (C.B.S.E. 2014)
Solution:

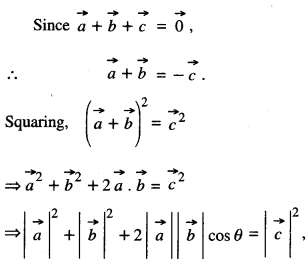
where ‘θ’ is the angle between a and b
⇒ (3)² + (5)² + 2 (3) (5) cos θ = (7)²
⇒9 + 25 + 30 cos θ = 49
⇒ 30 cos θ = 49 – 34 ⇒ cos θ = \(\frac{1}{2}\)
⇒ θ = 60°.
Hence, the angle between \(\vec{a}\) and \(\vec{b}\) is 60°.

Question 5.
If \(\vec{a}, \vec{b}, \vec{c}\) are mutually perpendicular vectors of equal magnitude, show that \(\vec{a}+\vec{b}+\vec{c}\) is equally inclined to \(\vec{a}, \vec{b}\) and \(\vec{c}\) . Also, find the angle, which \(\vec{a}+\vec{b}+\vec{c}\) makes with \(\vec{a}\) or \(\vec{b}\) or \(\vec{c}\) . (C.B.S.E. 2017)
Solution:

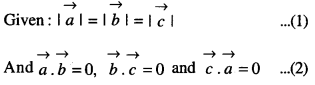
Let α, β and γ be the angles which \(\vec{a}+\vec{b}+\vec{c}\)
makes with \(\vec{a}, \vec{b}\) and \(\vec{c}\) respectively.

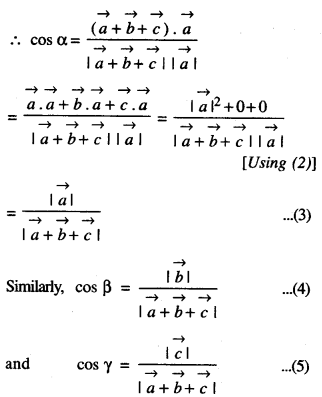
From (1), (3), (4) and (5),
cos α = cos β = cos γ ⇒ α = β = γ
Hence, \(\vec{a}+\vec{b}+\vec{c}\) is equally inclined to \(\vec{a}, \vec{b}\) and \(\vec{b}\)

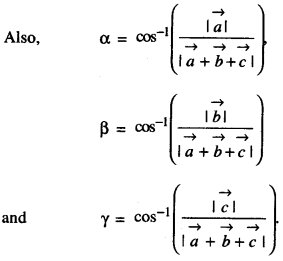
Question 6.
If with reference to a right-handed system of mutually perpendicular unit vectors
\(\hat{i}, \hat{j}, \hat{k}, \vec{\alpha}=3 \hat{i}-\hat{\jmath}\) where \(\vec{\beta}=2 \hat{i}+\hat{j}-3 \hat{k}\) then express \(\vec{\beta}\) in the form \(\vec{\beta}=\vec{\beta}_{1}+\vec{\beta}_{2}\) ,
where \(\vec{\beta}_{1}\) is parallel to \(\vec{\alpha}\) and \(\vec{\beta}_{2}\) is perpendicular to \(\vec{\alpha}\) . (N.C.E.R.T.; C.B.S.E. (F) 2013)
Solution:

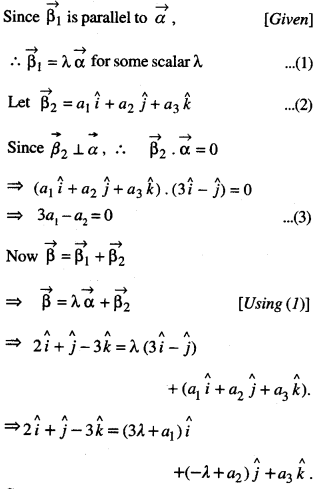
Comparing co-efficients, 2 = 3λ + a₁
1= – λ + a₂ , – 3 = a3
⇒ a₁= 2 – 3λ, a₂ = 1 + λ,
a₃ = -3 …(4)
Putting in (3), 3 (2-3λ)-(1 + λ) = 0
⇒ – 10λ +5 = 0
= λ = \(\frac { 1 }{ 2 }\)
From (4) a₁ = 2 – 3\(\frac { 1 }{ 2 }\) = 2-\(\frac { 3 }{ 2 }\) = \(\frac { 1 }{ 2 }\)
and a₂ = 1 + \(1+\frac{1}{2}=\frac{3}{2}\)

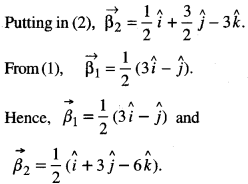
Question 7.
If \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\) find: \((\vec{r} \times \hat{i}) \cdot(\vec{r} \times \hat{j})+x y\) (C.B.S.E 2015)
Solution:

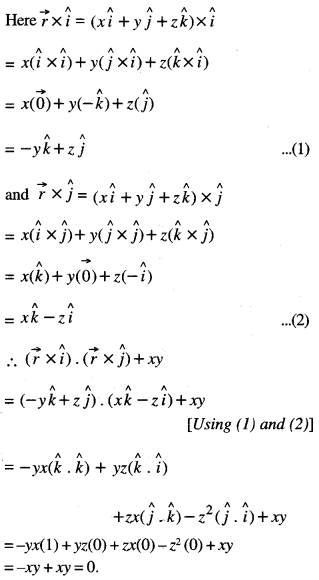
Question 8.
Show that the points A, B, C with position vectors \(2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}\) and \(3 \hat{i}-4 \hat{j}-4 \hat{k}\) respectively, are the vertices of a right angled triangle. Hence, find the area of the triangle. (A.I.C.B.S.E. 2017)
Solution:
Let(2\(\hat{i}\) – \(\hat{i}\) + \(\hat{k}\)), \(\hat{i}\) -3\(\hat{j}\) – 5\(\hat{k}\))
and (3\(\hat{i}\) -4\(\hat{j}\) -4\(\hat{k}\)) be the position vectors of the vertices A, B and C respectively.
.-. AB = (\(\hat{i}\) – 3\(\hat{j}\) – 5\(\hat{k}\)) – (2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\))
= – \(\hat{i}\) – 2\(\hat{j}\) – 6\(\hat{k}\)
BC = (3\(\hat{i}\) -4\(\hat{j}\) – 4\(\hat{k}\))-(\(\hat{i}\) -3\(\hat{j}\) – 5\(\hat{k}\))
= 2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\)
and = (2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\)) -(3\(\hat{i}\) – 4\(\hat{j}\) – 4\(\hat{k}\))
= – \(\hat{i}\) + 3 \(\hat{j}\) + 5\(\hat{k}\).
Now, \(\overrightarrow{\mathrm{BC}} \cdot \overrightarrow{\mathrm{CA}}\) = (2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\)). ( – \(\hat{i}\) + 3\(\hat{j}\) + 5\(\hat{k}\))
= (2)(-1) + (-1)(3) + (1)(5) = -2 -3 + 5 = 0.
Thus, \(\overrightarrow{\mathrm{BC}} \perp \overrightarrow{\mathrm{CA}}\)
⇒ ∠C = 90°.
Hence, AABC is rt. angled.

And, area of triangle = \(\frac{1}{2}|\overrightarrow{\mathrm{CA}} \times \overrightarrow{\mathrm{CB}}|\) ………… (1)
But \(\overrightarrow{\mathrm{CA}} \times \overrightarrow{\mathrm{CB}}=\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
-1 & 3 & 5 \\
-2 & 1 & -1
\end{array}\right|\)
= \(\hat{i}\)(-3-5) – \(\hat{j}\)(1 + 10) + \(\hat{k}\)(-1 + 6)
= -8\(\hat{i}\) – 11\(\hat{i}\) + 5\(\hat{i}\)
∴ \(|\overrightarrow{\mathrm{CA}} \times \overrightarrow{\mathrm{CB}}|=\sqrt{64+121+25}=\sqrt{210}\)
Hence, area of triangle = \(\frac{1}{2} \sqrt{210}\) sq. units

Question 9.
Find the value of ‘λ’ if four points with position vectors \(\mathbf{3} \hat{i}+6 \hat{j}+9 \hat{k}, \hat{i}+2 \hat{j}+3 \hat{k}\), \(2 \hat{i}+3 \hat{j}+\hat{k}\) and \(4 \hat{i}+6 \hat{j}+\lambda \hat{k}\) are coplanar.   (A.I.C.B.S.E. 2017)
Solution:
Let A, B, C and D be the points with position

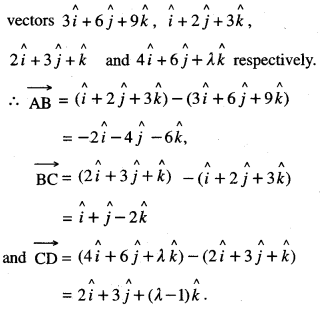
The four points are coplanar if \(\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}\) are coplanar

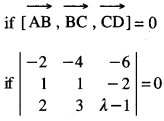
if – 2(λ – 1 +6) + 4(λ – 1 + 4) -6 (3 – 2) = 0
if -2λ.-10 + 4λ + 12 – 6 = 0
if 2λ,- 4 = 0 if λ = 2.
Hence, λ, = 2.

Question 10.
Let \(\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=\hat{i}\) and \(\vec{c}=c_{1} \hat{i}+c_{2} \hat{j}+c_{3} \hat{k}\). Then :
(a) Let c₁ = 1 and c₂ = 2, find c₃ which makes \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar
(b) Let c₂ = -1 and c₃ = 1, show that no value of c₁ can make \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar. (C.B.S.E. 2017)
Solution:
We have : \(\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=\hat{i}\) and
\(\vec{c}=c_{1} \hat{i}+c_{2} \hat{j}+c_{3} \hat{k}\)
(a) Here c₁ = 1 and c₂ = 2.
∴ \(\vec{c}=\hat{i}+2 \hat{j}+c_{3} \hat{k}\)
Since \(\vec{a}, \vec{b} \text { and } \vec{c}\) are coplanar, [Given]
∴ \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 0 \\
1 & 2 & c_{3}
\end{array}\right|=0\)
⇒ (-1) [c₃ – 2] = 0
⇒ c₃ – 2 = 0
⇒ c₃ = 2.

(b) Here c₂ = -1, c₃ = 1.
∴ \(\vec{c}=c_{1} \hat{i}-\hat{j}+\hat{k}\)
Since \(\vec{a}, \vec{b} \text { and } \vec{c}\) are coplanar, [Given]
∴ \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 0 \\
c_{1} & -1 & 1
\end{array}\right|=0\)
⇒ (-1) [1 +1] = 0
⇒ -2 = 0, which is false.
Hence, no value of c₁ can make \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar.

Question 11.
Show that the vectors \(\vec{a}, \vec{b} \text { and } \vec{c}\)are coplanar if \(\vec{a}+\vec{b}, \vec{b}+\vec{c}\) and \(\vec{c}+\vec{a}\) are coplanar. (N.C.E.R.T. (Supplement); (C.B.S.E. 2016)
Solution:

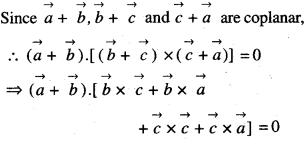
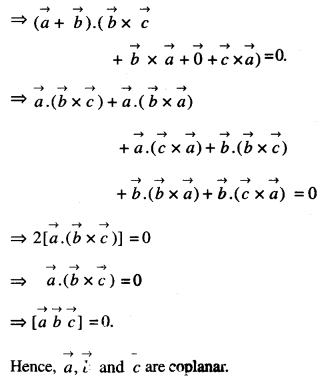
Question 12.
Prove that \([\overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}}, \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{a}}]=\mathbf{2}\left[\begin{array}{ccc}
\rightarrow & \overrightarrow{\mathbf{b}} & \overrightarrow{\mathbf{c}}
\end{array}\right]\)
(N.C.E.R.T. (Supplement); C.B.S.E. 2014)
Solution:

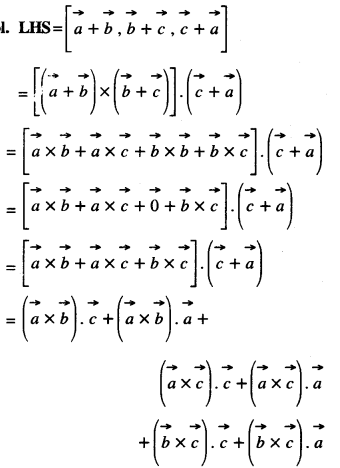
Question 13.
Show that the four points A, B, C and D with position vectors: \(\hat{i}+2 \hat{j}-\hat{k}, 3 \hat{i}-\hat{j}, 2 \hat{i}+3 \hat{j}+2 \hat{k}\) and \(4 \hat{i}+3 \hat{k}\) respectively are coplanar. (C.B.S.E. 2019 C)
Solution:

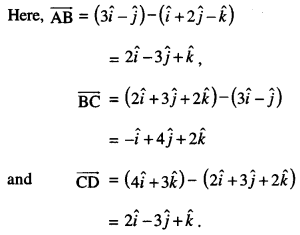
The four points A, B, C and D are coplanar ⇒ [AB,BC,CD]=O
⇒ \([\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}]=0\)
⇒ \(\left|\begin{array}{ccc}
2 & -3 & 1 \\
-1 & 4 & 2 \\
2 & -3 & 1
\end{array}\right|=0\)
⇒ 2(4 + 6) + 3 (-1 – 4) + 1.(3 – 8) = 0
⇒ 20 – 15 – 5 = 0
⇒ 0 = 0, which is true.