Matrices Class 12 Important Extra Questions Maths Chapter 3

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 3 Matrices. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 3 Important Extra Questions Matrices

Matrices Important Extra Questions Short Answer Type

Question 1.
Write the element a₂₃ of a 3 x 3 matrix A = [a_ij] whose elements atj are given by : \(\frac{|i-j|}{2}\)
Solution:
We have [a_ij] = \(\frac{|i-j|}{2}\)
∴ a₂₃ = \(\frac{|2-3|}{2}=\frac{|-1|}{2}=\frac{1}{2}\)

Question 2.
For what value of x is
\(\left[\begin{array}{lll}
1 & 2 & 1
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 0 \\
2 & 0 & 1 \\
1 & 0 & 2
\end{array}\right]\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]=0\) ? (C.B.S.E. 2019(C))
Answer:
We have
\(\left[\begin{array}{lll}
1 & 2 & 1
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 0 \\
2 & 0 & 1 \\
1 & 0 & 2
\end{array}\right]\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]=0\)

[1 + 4 + 1 2 + 0 + 0 0 + 2 + 2] \(\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0
[6 2 4 ]\(\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0
⇒ [0 + 4 + 4x] =0
⇒ [4 + 4x] = [0]
⇒ 4 + 4x = 0.
Hence, x = -1.

Question 3.
Find a matrix A such that 2A – 3B + 5C = 0,
Where B = \(\left[\begin{array}{ccc}
-2 & 2 & 0 \\
3 & 1 & 4
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
2 & 0 & -2 \\
7 & 1 & 6
\end{array}\right]\)
Solution:
Here, 2A – 3B + 5C = 0
⇒ 2A = 3B – 5C

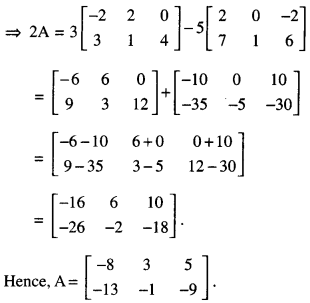
Question 4.
If A = \(\left(\begin{array}{l}
\cos \alpha-\sin \alpha \\
\sin \alpha-\cos \alpha
\end{array}\right)\) , then for what value of ‘α’ is A an identity matrix? (C.B.S.E. 2010)
Solution:
Here A = \(\left(\begin{array}{l}
\cos \alpha-\sin \alpha \\
\sin \alpha-\cos \alpha
\end{array}\right)\)
Now A = I = \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\) when
cos α = 1 and sin α = 0.
Hence, α = 0.

Question 5.
Find the values of x, y, z and t, if:
\(2\left[\begin{array}{ll}
x & z \\
y & t
\end{array}\right]+3\left[\begin{array}{rr}
1 & -1 \\
0 & 2
\end{array}\right]=3\left[\begin{array}{ll}
3 & 5 \\
4 & 6
\end{array}\right]\)
Solution:
We have :

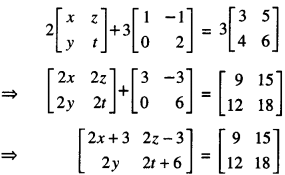
⇒ 2x + 3 = 9 …………. (1)
2z – 3 = 15 …………. (2)
2y = 12 …………. (3)
2t + 6 = 18 …………. (4)

From (1), ⇒ 2x = 9 – 3
⇒ 2x = 6
⇒ x = 3.

From (3) 2y = 12
⇒ y = 6.

From (2), ⇒ 2z – 3 = 15
⇒ 2z = 18
⇒ z = 9.

From (4), 2t + 6 = 18
⇒ 2t = 12
⇒ t = 6.
Hence, x = 3,y = 6, z = 9 and t = 6.

Question 6.
If A = \(\left[\begin{array}{rrr}
2 & 0 & 1 \\
2 & 1 & 3 \\
1 & -1 & 0
\end{array}\right]\), then find (A² – 5A). (CBSE 2019)
Solution:
We have A = \(\left[\begin{array}{rrr}
2 & 0 & 1 \\
2 & 1 & 3 \\
1 & -1 & 0
\end{array}\right]\)
Then A² = AA

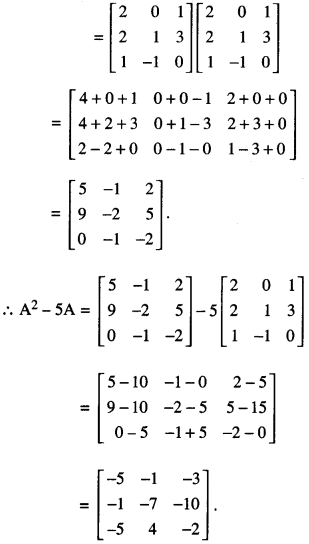
Question 7.
If A = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\) and I = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) , find k so that A² = 5A + b kI (C.B.S.E. Sample Paper 2018-2019)
Solution:

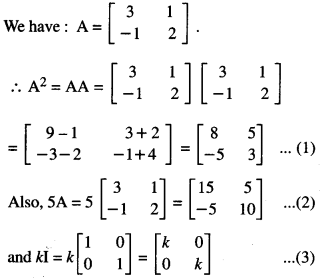
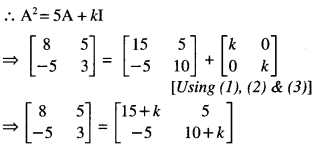
⇒ 8 = 15 + k and 3 = 10 + k
⇒ k = -1 and k = -7.
Hence, k – -7.

Question 8.
If A and B are symmetric matrices, such that AB and BA are both defined, then prove that AB – BA is a skew symmetric matrix. (A.I.C.B.S.E. 2019)
Solution:
Since A and B are symmetric matrices,
∴ A’ = A and B’ = B …(1)
Now,(AB – BA)’= (AB)’ – (BA)’
= B’A’ – A’B’
= BA – AB [Using (1)]
= – (AB – BA).
Hence, AB – BA is a skew-symmetric matrix.

Question 9.
For the matrix A = \(\left[\begin{array}{ll}
2 & 3 \\
5 & 7
\end{array}\right]\) find (A + A’) and show that it is a symmetric matrix. (A.I.C.B.S.E. 2019)
Solution:

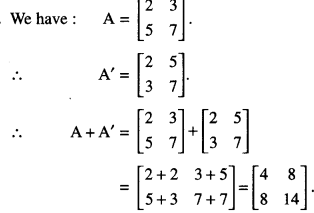
Now (A + A’)’ = \(\left[\begin{array}{cc}
4 & 8 \\
8 & 14
\end{array}\right]\) = (A + A’)
Hence (A + A’) is symmetric

Question 10.
If the matrix A = \(\left[\begin{array}{ccc}
0 & a & -3 \\
2 & 0 & -1 \\
b & 1 & 0
\end{array}\right]\) is skew symmetric, find the values of ‘a’ and ‘b’: (C.B.S.E. 2018)
Solution:

Comparing, 2 = -a ⇒ a = -2
and – 3 = -b ⇒ b = 3.
Hence, a = -2 and b = 3.

Matrices Important Extra Questions Long Answer Type 1

Question 1.
Find the values of a, b, c and d from the following equation :
\(\left[\begin{array}{cc}
2 a+b & a-2 b \\
5 c-d & 4 c+3 d
\end{array}\right]=\left[\begin{array}{cc}
4 & -3 \\
11 & 24
\end{array}\right]\) (N.C.E.R.T)
Solution:
We have
\(\left[\begin{array}{cc}
2 a+b & a-2 b \\
5 c-d & 4 c+3 d
\end{array}\right]=\left[\begin{array}{cc}
4 & -3 \\
11 & 24
\end{array}\right]\)
Comparing the corresponding elements of two given matrices, we get:
2a + b = 4 …(1)
a-2b = – 3 …(2)
5c-d = 11 …(3)
4c + 3d = 24 …(4)
Solving (1) and (2):
From (1),
b = 4 – 2a …(5)
Putting in (2), a – 2 (4 – 2a) = – 3
⇒ a – 8 + 4a = -3
⇒ 5a = 5
⇒ a = 1.
Putting in (5),
b = 4 – 2(1) = 4 – 2 = 2.
Solving (3) and (4):
From (3),
d = 5c- 11 …(6)
Putting in (4),
4c+ 3 (5c- 11) = 24
⇒ 4c + 15c – 33 = 24
⇒ 19c = 57
⇒ c = 3.
Putting in (6),
d = 5 (3) – 11 = 15 – 11 = 4.
Hence, a = 1, b = 2, c = 3 and d = 4.

Question 2.
If \(\left[\begin{array}{rrr}
9 & -1 & 4 \\
-2 & 1 & 3
\end{array}\right]\) = A + \(\left[\begin{array}{rrr}
1 & 2 & -1 \\
0 & 4 & 9
\end{array}\right]\) then find the matrix A. (C.B.S.E. 2013)
Solution:

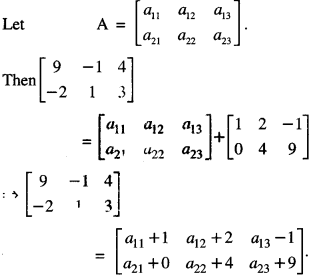
Comparing:
9 = a₁₁ + 1 – 1 = a₁₂ + 2,
4 = 1₁₃ – 1, -2 = a₂₁
1 = a₂₂ + 4, and 3 = a₂₃ + 9
a₁₁ = 8, a₁₂ = – 3,
a₁₃ = 5, a₂₁ = -2
a₂₂ = – 3, and a₂₃ = – 6.
Hence, A = \(\left[\begin{array}{rrr}
8 & -3 & 5 \\
-2 & -3 & -6
\end{array}\right]\)

Question 3.
If A = \(=\left[\begin{array}{rr}
2 & 2 \\
-3 & 1 \\
4 & 0
\end{array}\right]\) B = \(\left[\begin{array}{ll}
6 & 2 \\
1 & 3 \\
0 & 4
\end{array}\right]\)find the matrix C such that A + B + C is a zero matrix.
Solution:

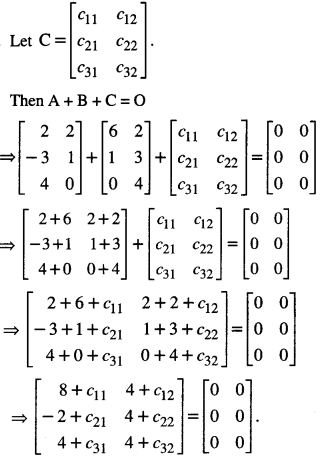
Comparing :
8 + c₁₁ = 0 ⇒ c₁₁ = -8,
4 + C₁₂ = 0 ⇒ C₁₂ = -4,
– 2 + C₂₁ = 0 ⇒ C₂₁ = 2
4 + C₂₂ = 0 ⇒ C₂₂ =- 4,
4 + c₃₁ = 0 ⇒ C₃₁ = -4
and 4 + c₃₂ = 0 ⇒ C₃₂ = -4.
Hence, C = \(\left[\begin{array}{rr}
-8 & -4 \\
2 & -4 \\
-4 & -4
\end{array}\right]\)

Question 4.
If A = \(\left[\begin{array}{rr}
8 & 0 \\
4 & -2 \\
3 & 6
\end{array}\right]\) B = \(\left[\begin{array}{rr}
2 & -2 \\
4 & 2 \\
-5 & 1
\end{array}\right]\) then find the matrix ‘X’, of order 3 x 2, such that 2A + 3X = 5B. (N.C.E.R.T.)
Solution:
We have : 2A + 3X = 5B
⇒ 2A + 3X-2A = 5B-2A
⇒ 2A-2A + 3X = 5B-2A
⇒ (2A – 2A) + 3X = 5B – 2A
⇒ O + 3X = 5B – 2A
[ ∵ – 2A is the inverse of2A]
⇒ 3X = 5B – 2A.
[ ∵ O is the additive identity]
Hence, X = \(\frac{1}{3}\)(5B – 2A)

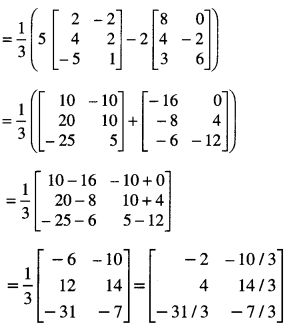
Question 5.
If A is a square matrix such that A2 = A, then write the value of 7A – (I + A)3, where I is an identity matrix. (A.I.C.B.S.E. 2014)
Solution:
(I + A)² = (I + A) (I + A)
= II + IA + AI + AA
= I + A + A + A²
= I + 2A + A [∵ A² = A]
= I + 3A …(1)
∴ (I + A)³ = (I + A)² (I + A)
= (I + 3A) (I + A) [Using (1)]
= II + IA + 3AI + 3AA
= I + A + 3A + 3A²
= I + A + 3A + 3A [∵ A² = A]
= I + 7 A …(2)
Hence, 7A – (I + A)³ = 7A – (I + 7A)
[Using (2)]
= -I.

Question 6.
Compute the indicated product:
\(\left[\begin{array}{lll}
2 & 3 & 4 \\
3 & 4 & 5 \\
4 & 5 & 6
\end{array}\right]\left[\begin{array}{rrr}
1 & -3 & 5 \\
0 & 2 & 4 \\
3 & 0 & 5
\end{array}\right]\) (NCERT)
Solution:

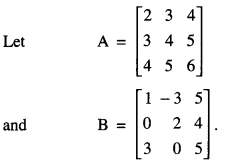
Number of columns of A = Number of rows of B = 3.
Thus AB is defined and is a 3 x 3 matrix.


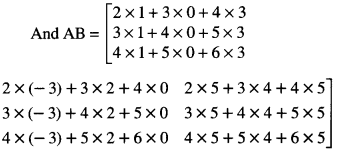
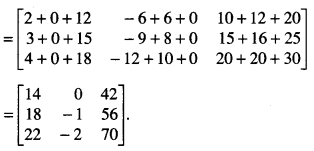
Question 7.
IF A = \(\), show that A² – 6A² + 7A + 2I = 0   (N.C.E.R.T)
Solution:

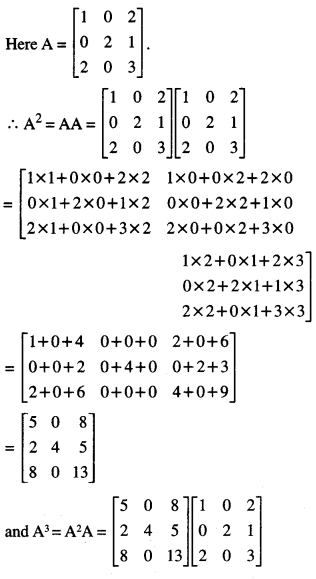
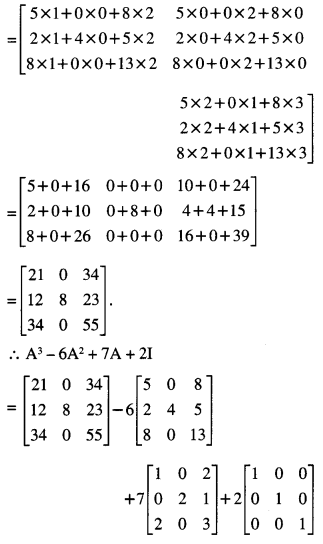
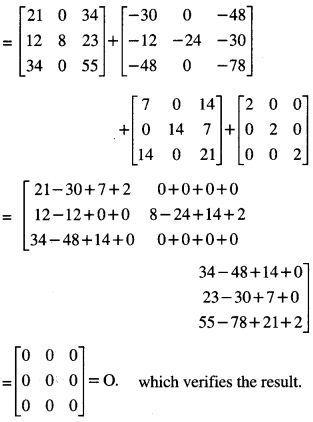
Question 8.
Prove the following by the principle of Mathematical Induction:
If A = \(\left[\begin{array}{ll}
3 & -4 \\
1 & -1
\end{array}\right]\)
than An = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\) (N.C.E.R.T)
Solution:
Set I. When n = 1

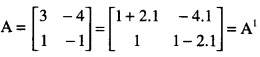
Thus the result is true when n = 1.
Step II. Let us assume that the result is true for any natural number m, where 1 ≤ m ≤ n

Thus the result is true when n = m+ 1.
Hence, by Mathematical Induction, the required result is true for all n ∈ N.

Question 9.
If A = \(\left[\begin{array}{r}
-2 \\
4 \\
5
\end{array}\right]\), B = [1 3 -6], then verify that (AB)’ = B’A’ (N.C.E.R.T.)
Solution:
We have :
A = \(\left[\begin{array}{r}
-2 \\
4 \\
5
\end{array}\right]\), B = [1 3 -6]

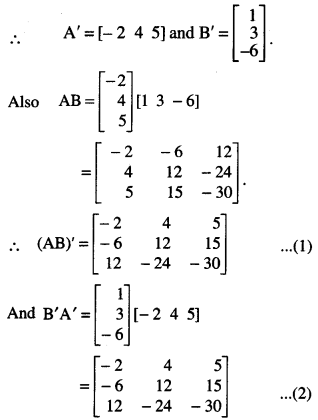
From (1) and (2), (AB)’ = B’A’
which verifies the result.

Question 10.
By using elementary transformations, find the inverse of the matrix A = \(\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\)
(N.C.E.R.T.)
Solution:
(By Elementary Row Transformations)
We know A = I₂A

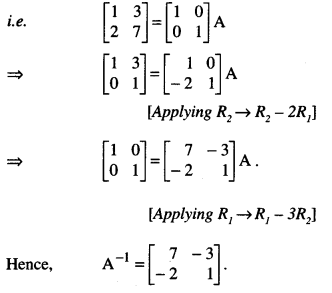
Matrices Important Extra Questions Long Answer Type 2

Question 1.
Two farmers Ram Kishan and Gurucharan Singh cultivate only three varieties of rice namely Basmati, Permal and Naura. The sale (in ?) of these varieties of rice by both the farmers in the month of September and October are given by the following matrices A and B :

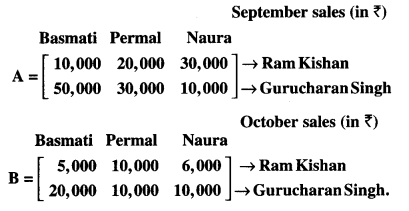
Find :
(i) What were combined sales in September and October for each farmer in each variety?
(ii) What was the change in sales from September to October?
(iii) If both farmers receive 2% profit on gross sales, compute the profit for each farmer and for each variety in October. (N.C.E.R.T.)
Solution:
(i) Combined sales in September and October :

(ii) Change in sales from September to October:

(iii) 2% of B = \(\frac{2}{100}\) x B = 0.02 B

Hence, Ram Kishan receives ₹ 100, ₹ 200 and ₹ 120 as profit and Gurucharan Singh receives ₹ 400, ₹200 and ₹ 200 in each variety of rice in the month of October.

Question 2.
Three schools A, B and C organised a mela for collecting funds for helping the rehabilitation of flood victims. They sold handmade fans, mats and plates from recycled meterial at a cost of ₹25, ₹100 and ₹50 each. The number of articles sold are given below :

Find the funds collected by each school separately by selling the above articles. Also, find the total fund collected for the purpose.
(C.B.S.E. 2015)
Solution:
Quantity matrix, A = \(\left[\begin{array}{lll}
40 & 25 & 35 \\
50 & 40 & 50 \\
20 & 30 & 40
\end{array}\right]\)
Cost Matrix B = [laatex]\left[\begin{array}{c}
25 \\
100 \\
50
\end{array}\right][/latex]
Total fund = Quantity matrix x Cost matrix

Fund collected by school A = ₹5,250
Fund collected by school B = ₹7,750
Fund collected by school C = ₹5,500 and total fund collected = 5250 + 7750 + 5500
= ₹18,500.

Question 3.
If A = \(\left(\begin{array}{rr}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right)\), find α satisfing 0 < α < when A + A^T = √2I₂
Where A^T is transpose of A. (A.I.C.B.S.E. 2016)
Solution:

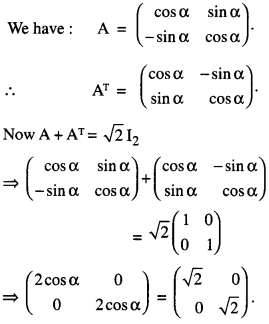
Question 4.
If \(\left(\begin{array}{cc}
a+b & 2 \\
5 & b
\end{array}\right)\) = \(\left(\begin{array}{ll}
6 & 5 \\
2 & 2
\end{array}\right)^{\prime}\) (C.B.S.E. 2010C)
Solution:

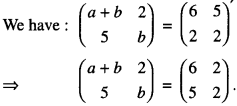
Comparing:
a + b – 6 ………….. (1)
and b = 2 ………….(2)
Putting the value of b from (2) in (1),
a + 2 = 6.
Hence, a = 4.

Question 5.
Express the matrix A as the sum of a symmetric and a skew-symmetric matrix, where :
A = \(\left[\begin{array}{rrr}
3 & -2 & -4 \\
3 & -2 & -5 \\
-1 & 1 & 2
\end{array}\right]\) (A.I.C.B.S.E. 2010)
Solution:
We have

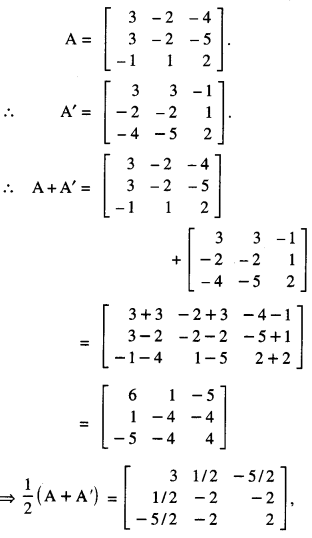
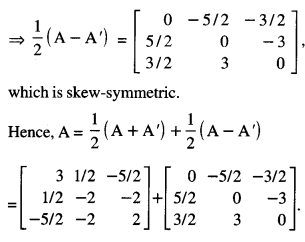
Question 6.
Find the inverse of the following matrix, using elementary operations :
A = \(\left[\begin{array}{ccc}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{array}\right]\)  (C.B.S.E. 2019)
Solution:
We know that A + I₃A\

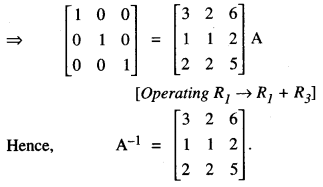
Question 7.
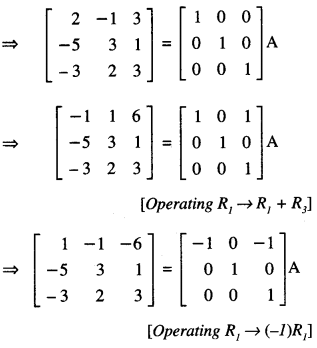
Find the inverse of the following matrix, using elementary transformation:
\(\left[\begin{array}{rrr}
2 & -1 & 3 \\
-5 & 3 & 1 \\
-3 & 2 & 3
\end{array}\right]\)  (C.B.S.E. Sample Paper 2017-18)
Solution:
We know that A = IA

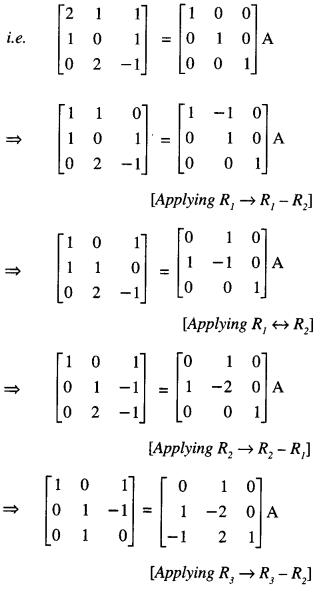
Question 8.
If A = \(\left[\begin{array}{rrr}
2 & 1 & 1 \\
1 & 0 & 1 \\
0 & 2 & -1
\end{array}\right]\) , find the inverse of A, using elementary row transformations and hence solve the following equation:
XA = [1 0 1 ] (C.B.S.E. Sample Paper 2017-18)
Solution:
(i) We know that A = I₃ A

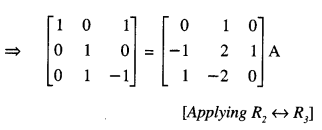
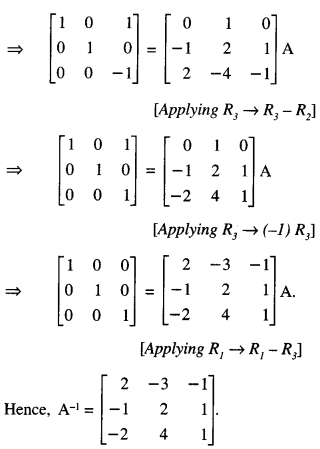
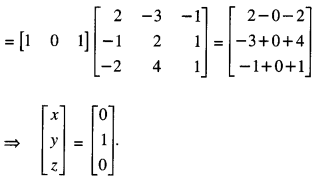
Here, x = 0, y = 1, z = 0