Determinants Class 12 Important Extra Questions Maths Chapter 4

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 4 Determinants. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 4 Important Extra Questions Determinants

Determinants Important Extra Questions Very Short Answer Type

Question 1.
Find the co-factor of the element a₂₃ of the determinant:
\(\left|\begin{array}{lll}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & 3
\end{array}\right|\)
(C.B.S.E. 2019 C)
Solution:
Co-factor of a₂₃ = (-1)^{2 + 3} \(\left|\begin{array}{ll}
5 & 3 \\
1 & 2
\end{array}\right|\)
= (-1)⁵ (5 x 2 – 1 x 3)
= (-1) (10-3)
= (-1) (7) = -7.

Question 2.
If A and B are invertible matrices of order 3, |A| = 2 and |(AB)^-1| = \(-\frac{1}{6}\) Find |B|.
(C.B.S.E. Sample Paper 2018-19)
Solution:


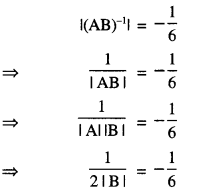
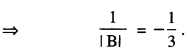
Hence |B| = 3

Question 3.
Check whether (l + m + n) is a factor of the determinant \(\left|\begin{array}{ccc}
l+m & m+n & n+l \\
n & l & m \\
2 & 2 & 2
\end{array}\right|\) or not.
Given reason.
(C.B.S.E. Sample Paper 2020)
Solution:
Given

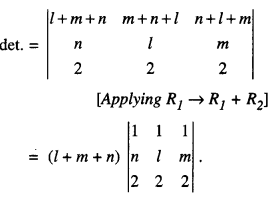
Hence, (l + m + n) is a factor of given determinant.

Question 4.
If A is a square matrix of order 3, with |A| = 9, then write the value of |2 . adj. A|.   (A.I.C.B.S.E. 2019)
Solution:
| 2 – adj. A| = 2³ | A |^3-1
= 8(9)²
= 648.

Question 5.
If A and B are square matrices of the same order 3, such that |A| = 2 and AB = 2I, write the value of IBI. (C.B.S.E. 2019)
Solution:
We have : AB = 2I
∴ |AB| = |2I|
⇒ |A||B| = |2I|
⇒ 2|B|= 2(1).
Hence,|B| = 1.

Question 6.
A is a square matrix with |A| = 4. Then find the value of |A. (adj. A) |.
(A.I.C.B.S.E. 2019)
Solution:
|A . (adj. A) | = |A|ⁿ
= 4ⁿ or 16 or 64.

Question 7.
If Δ = \(\left|\begin{array}{lll}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & 3
\end{array}\right|\) , write:
(i) the minor of the element a₂₃ (C.B.S.E. 2012)
(ii) the co-factor of the element a₃₂. (C.B.S.E. 2012)
Solution:
(i) a₂₃ = \(\left|\begin{array}{ll}
5 & 3 \\
1 & 2
\end{array}\right|\)
= (5) (2) – (1) (3)
= 10 – 3 = 7.

(ii) a₃₂ = (-1)³⁺² \(\left|\begin{array}{ll}
5 & 8 \\
2 & 1
\end{array}\right|\)
= (-1)⁵ [(5) (1) – (2) (8)]
= (-1)⁵ (5 – 16)
= (- 1) (- 11) = 11.

Question 8.
Find the adjoint of the matrix A = \(\left[\begin{array}{cc}
2 & -1 \\
4 & 3
\end{array}\right]\) (A.I.C.B.S.E. 2010)
Solution:
Here |A| = \(\left[\begin{array}{cc}
2 & -1 \\
4 & 3
\end{array}\right]\)
Now A₁₁ = Co-factor of 2 = 3,
A₁₂ = Co-factor of – 1 = – 4,
A₂₁ = Co-factor of 4 = 1
and A₂₂ = Co-factor of 3 = 2
∴ Co-factor matrix = \(\left[\begin{array}{rr}
3 & -4 \\
1 & 2
\end{array}\right]\)
Hence, adj. A = \(\left[\begin{array}{rr}
3 & -4 \\
1 & 2
\end{array}\right]\) = \(\left[\begin{array}{rr}
3 & 1 \\
-4 & 2
\end{array}\right]\)

Question 9.
Given A = \(\left[\begin{array}{rr}
2 & -3 \\
-4 & 7
\end{array}\right]\) compute A^-1 and show that 2A^-1 = 9I – A. (C.B.S.E. 2018)
Solution:
(i) We have: A = \(\left[\begin{array}{rr}
2 & -3 \\
-4 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{cc}
2 & -3 \\
-4 & 7
\end{array}\right|\)
= (2) (7) – (-4) (-3)
= 14 – 12 = 2 ≠ 0.
∴ A^-1 exists and
A^-1 = \(\frac{1}{|\mathrm{~A}|}\) adj A = \(\frac{1}{2}\left[\begin{array}{ll}
7 & 3 \\
4 & 2
\end{array}\right]\)

(ii) RHS = 9I – A

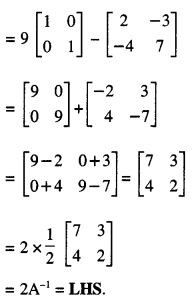
Question 10.
For what value of ‘x’, the matrix \(\left[\begin{array}{cc}
5-x & x+1 \\
2 & 4
\end{array}\right]\) is singular? (C.B.S.E. 2011)
Solution:
The matrix \(\left[\begin{array}{cc}
5-x & x+1 \\
2 & 4
\end{array}\right]\) is singular
⇒ \(\left[\begin{array}{cc}
5-x & x+1 \\
2 & 4
\end{array}\right]\) = 0
⇒ 4(5 -x) – 2 (x + 1) = 0
⇒ 20 – 4x – 2x – 2 = 0
⇒ 18 – 6x = 0
⇒ 6x = 18.
Hence, x = 3.

Determinants Important Extra Questions Long Answer Type 1

Question 1.
Using properties of determinants, prove the following :

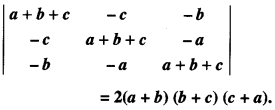
(C.B.S.E. 2019)
Solution:

[Operating C₃ → C₃ + C₂]
= (a + b) (a + c) (2) [c + b]
= 2(a + b) (b + c) (c + a) = RHS.

Question 2.
If f(x) = \(\left|\begin{array}{rrr}
a & -1 & 0 \\
a x & a & -1 \\
a x^{2} & a x & a
\end{array}\right|\), using properties of determinants, find the value   (C.B.S.E. 2015)
Solution:
We have


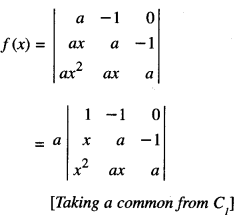
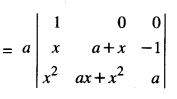
[Operating C₂ → C₂ + C₁]
= a[(a + x) a + (ax + x²)]
= a[a² + ax + ax + x²]
= a(x² + 2 ax + a²)
= a(x + a)².
f(2x) = a(2x + a)²,
f (2x) -f(x) = a[(2x + a)² – (x + a)²]
= a[(4x² + 4 ax + a²) – (x² + 2ax + a²)]
= a(3x² + 2 ax)
= ax(3x + 2a).

Question 3.
Using properties of determinants, prove that:
\(\left|\begin{array}{ccc}
1 & 1 & 1+3 x \\
1+3 y & 1 & 1 \\
1 & 1+3 z & 1
\end{array}\right|\) = 9(3xyz + xy + yz + zx) (C.B.S.E. 2018)
Solution:

1 . (0 + 9yz) + 3x(3 z + 9yz + 3y)
= 9(3xyz + xy + yz + zx) = RHS

Question 4.
Using properties of determinants, prove that:
\(\left|\begin{array}{ccc}
a & b-c & c+b \\
a+c & b & c-a \\
a-b & b+a & c
\end{array}\right|\) = (a + b + c) (a² + b² + c²) (C.B.S.E. Sample Paper 2018-19)
Solution:

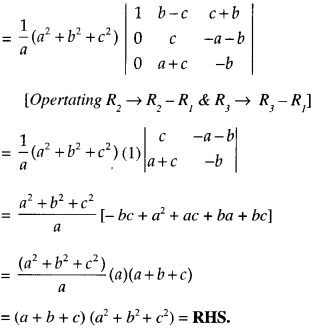
Question 5.
Using properties of determinants, prove that:
\(\left|\begin{array}{ccc}
a^{2}+2 a & 2 a+1 & 1 \\
2 a+1 & a+2 & 1 \\
3 & 3 & 1
\end{array}\right|\) = (a – 1)³. (C.B.S.E. 2019)
Solution:

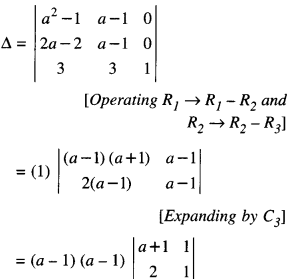
[Taking (a-1) common form R₁ and R₂]
= (a – 1)² [a + 1 -2]
= (a – 1)² (a – 1)
= (a – 1)³.

Question 6.
If x, y, z are different and \(\left|\begin{array}{lll}
x & x^{2} & 1+x^{3} \\
y & y^{2} & 1+y^{3} \\
z & z^{2} & 1+z^{3}
\end{array}\right|\) = 0 show that :
(i) 1 + xyz = 0
(ii) xyz = -1
Solution:



[Dividing by (x – y) (y – z) (z – x)
because x ≠ y y ≠ z z ≠ x

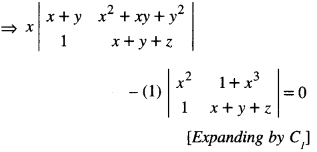
⇒ x [(x + y) (x + y + z) – (1) (x² + xy + y²)]
– [x² (x + y + z) – (1) (1 + x³)] = 0
⇒ x[x² + xy + zx + xy + y² + yz – x² – xy – y²] – [x³ + x²y + x²z – 1 – x³] = 0
⇒ x[xy + yz + zx]- [x²y + x²z – 1] = 0
⇒ x²y + xyz + zx² – x²y – x²z + 1 = 0
⇒ 1 + xyz = 0 or xyz = -1, which is

Question 7.
Prove that \(\begin{array}{c}
\left|\begin{array}{ccc}
1+a & 1 & 1 \\
1 & 1+b & 1 \\
1 & 1 & 1+c
\end{array}\right| \\
=a b c\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)
\end{array}\) = abc + ab + bc + ca (N.C.E.R.T.; A.I.C.B.S.E. 2013, 12, 10 C)
Solution:

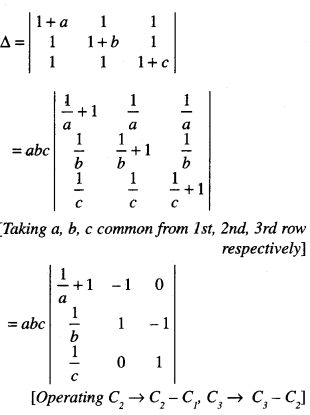
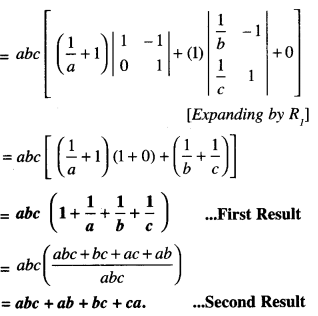
Question 8.
Using properties of determinants, find the value of k if
\(\left|\begin{array}{ccc}
x & y & x+y \\
y & x+y & x \\
x+y & x & y
\end{array}\right|\)= k(x³ + y³) (A.I.C.B.S.E. 2019)
Solution:
We have :

[Operating C₂ → C₂ – C₁ & C₃ → C₃ – C₁]
⇒ 2(x + y) (1) [-x² + y (x – y] = k(x³ + y³)
⇒ – 2(x + y) (x² – xy + y²) = k(x³ + y³)
⇒ – 2(x³ + y³) = k(x³ + y³).
Hence, k = – 2.

Question 9.
Using properties of determinants, prove the
following:
\(\left|\begin{array}{ccc}
a & b & c \\
a-b & b-c & c-a \\
b+c & c+a & a+b
\end{array}\right|\) = a³ + b³ + c³ – 3abc. (C.B.S.E. 2019)
Solution:

[Operating C₁ → C₁ – C₂ and C₂ → C₂ – C₃]
= (a + b + c) [(a – 2b + c) (c – b) – (b – 2c + a) (b – a)]
= (a + b + c)[a² + b² + c² – ab – bc – ca]
= a³ + b³ + c³ – 3abc = RHS

Question 10.
Prove the following, using properties of determinants:
\(\left|\begin{array}{ccc}
\alpha & \alpha^{2} & \beta \\
\beta & \beta^{2} & \gamma+\alpha \\
\gamma & \gamma^{2} & \alpha+\beta
\end{array}\right|\) = (β-γ)(γ-α)(α-β)(α+β+γ) (C.B.S.E. 2019 C)
Solution:


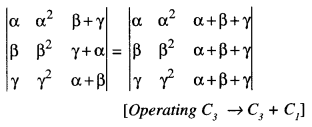
= (α + β + γ)(α – β)(β – γ)(γ + β – β – α)
= (β – γ)(γ – α)(α – β)(α + β + γ)
which is true.

Question 11.
Find the minors and co-factors of all elements of the determinant \(\left|\begin{array}{rr}
1 & -2 \\
4 & 3
\end{array}\right|\) . (N.C.E.R.T.)
Solution:
By definition,
M₁₁ = Minor of a₁₁ = 3
A₁₁ = Co-factor of a₁₁
= (- 1)¹⁺¹ M₁₁= (- 1)² 3 = 3

M₁₂ = Minor of a₁₂ = 4
A₁₂ = Co-factor of a₁₂
= (-1)^{1 + 2} M₁₂ = (-1)³ 4 = -4

M₂₁ = Minor of a₂₁ = – 2
A₂₁ = Co-factor of a₂₁
= (- 1)²⁺¹ M₂₁
= (- 1)³ (- 2)
= (- 1) (- 2) = 2

M₂₂ = Minor of = 1
A₂₂ = Co-factor of a₂₂
= (-1)²⁺² M₂₂ = (-1)⁴ (1) = 1.

Question 12.
For the matrix A = \(\left[\begin{array}{rr}
2 & -1 \\
3 & 2
\end{array}\right]\), show that A² – 4A + 7I = 0. Hence, obtain A^-1.
Solution:

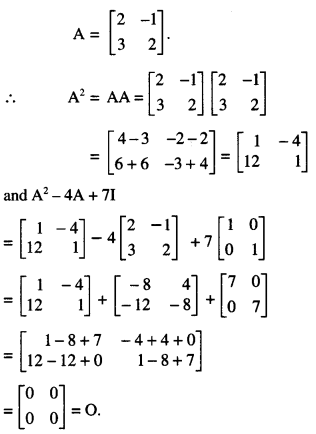
(ii) A² – 4A + 7I = 0
⇒ 7I = 4A-A²

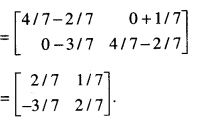
Question 13.
Using properties of determinants, find the value of x for which
\(\left|\begin{array}{lll}
4-x & 4+x & 4+x \\
4+x & 4-x & 4+x \\
4+x & 4+x & 4-x
\end{array}\right|\) = 0
(A.I.C.B.S.E. 2019)
Solution:

⇒ (12 + x) [4x²] = 0
⇒ x² (x + 12) = 0.
Hence, x = 0 or x = – 12.

Question 14.
If A = \(\left[\begin{array}{rrr}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right]\), find (A’)^-1 (C.B.S.E. 2015)
Solution:
We have


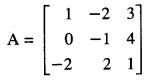
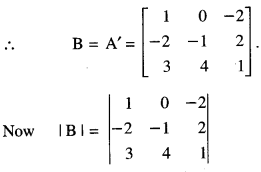
= (1)( – 1 – 8) – O – 2( – 8 + 3)
= – 9 + 10 = 1 ≠ 0
B exists.= (1)( – 1 – 8) – 0 – 2( – 8 + 3)
= -9 + 10 = 1 ≠ 0
B^-1 exists.

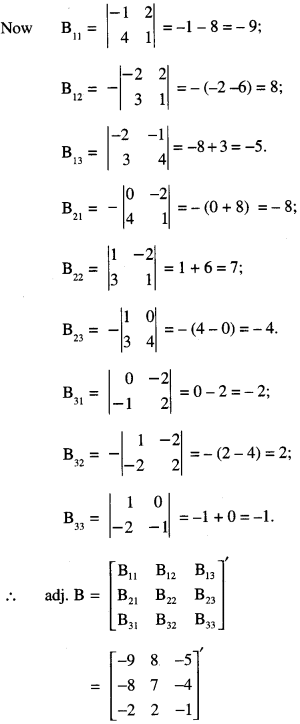
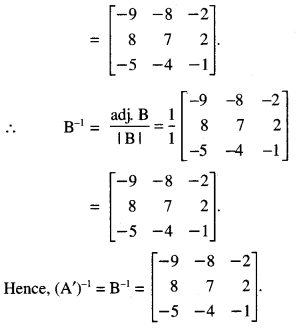
Question 15.
Using matrices, solve the following system of linear equations :
x + 2y -3z = – 4
2x + 3y + 2z = 2
3x – 3y – 4z = 11.   (A.I.C.B.S.E. 2019)
Solution:
We have A= \(\left[\begin{array}{ccc}
1 & 2 & -3 \\
2 & 3 & 2 \\
3 & -3 & -4
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ccc}
1 & 2 & -3 \\
2 & 3 & 2 \\
3 & -3 & -4
\end{array}\right|\)
=(1)( – 12 + 6) – (2)( – 8 – 6)+( – 3)( – 6 – 9)
= – 6 + 28 + 45 = 73 – 6 = 67.
∴ A is non-singular A exists.
Now, A₁₁ = -6, A₁₂ = 14. A₁₃ = -15
A₂₁ = 17, A₂₂ = 5, A₂₃ = 9
A₃₁ = 13, A₃₂ = – 8, A₃₃ = – 1


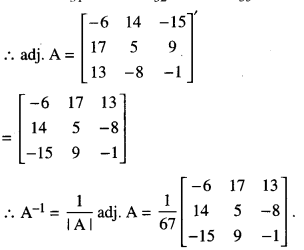
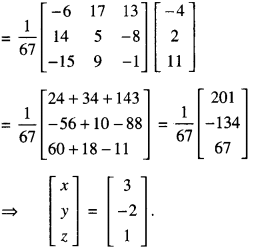
The given equation can be written as AX = B.
⇒ X = A^-1B
Hence x = 3, y = -2 and z = 1

Determinants Important Extra Questions Long Answer Type 2

Question 1.
Using the properties of determinants, prove that:
\(\mid \begin{array}{ccc}
(y+z)^{2} & x^{2} & x^{2} \\
y^{2} & (z+x)^{2} & y^{2} \\
z^{2} & z^{2} & (x+y)^{2}
\end{array}\) = 2xyz(x + y + z)³
(CBSE. Sample Paper 2019-20)
Solution:


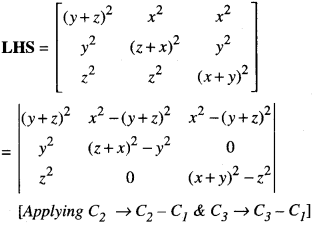
= 2(x + y + z)² [xyz² + x²yz + xy²z
+ y² z² – y² z² ]
= 2xyz (x + y + z)² (x + y + z)
= 2xyz (x + y + z)³ = RHS.

Question 2.
If A = \(\left[\begin{array}{ccc}
2 & 3 & 4 \\
1 & -1 & 0 \\
0 & 1 & 2
\end{array}\right]\), find A^-1 Hence , solve the system of equations.
x – y = 3;
2x + 3y + 4z = 17;
y + 2z = 7.
(C.B.S.E. 2019)
Solution:
(i) |A| = \(\left|\begin{array}{ccc}
2 & 3 & 4 \\
1 & -1 & 0 \\
0 & 1 & 2
\end{array}\right|\)
=2( – 2 – 0) – 3(2 – 0)+4(1 +0)
= – 4 – 6 + 4= – 6 ≠ 0
∴ A is non-singular and as such A exists.
Now, A₁₁ = -2, A₁₂ = -2. A₁₃ = 1
A₂₁ = -2, A₂₂ = 4, A₂₃ = -2
A₃₁ = 4, A₃₂ = 4, A₃₃ = -5

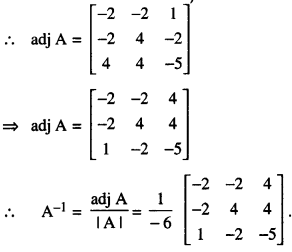
(II) The given system of equations can be written as AX = B,

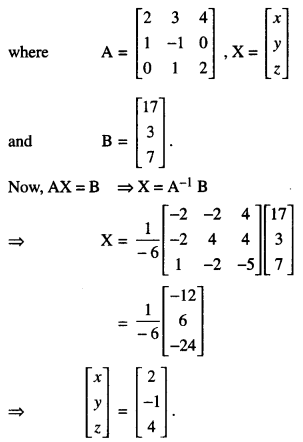
Hence x = 2, y = -1 and z = 4.

Question 3.
Obtain the inverse of the following matrix using elementary operations :
A = \(\left[\begin{array}{ccc}
-1 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]\) (C.B.S.E. 2019)
Solution:
We know that A = I₃A

Question 4.
If A = \(\left[\begin{array}{rrr}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\) , find A^-1. Use it to solve the system of equations:
2x – 3y + 5z = 11
3x + 2y – 4z = – 5
x + y – 2z = -3.   (C.B.S.E. 2019,18)
Solution:
(I) |A| = \(\left[\begin{array}{rrr}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\)
= 2 (- 4 + 4) + 3 (- 6 + 4) + 5 (3 – 2)
= 2 (0) + 3 (- 2) + 5 (1)
= 0 – 6 + 5 = -1 ≠ 0.
A is non-singular and as such A^-1 exists.

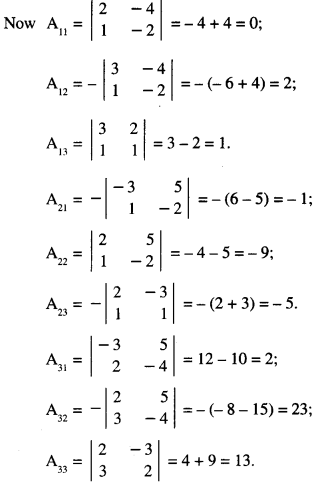
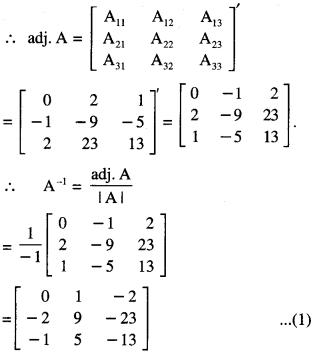
(II) The given system of equations is :
2x – 3y + 5z = 11
3x + 2y – 4z = -5
x + y – 2z = – 3.
These equations can be written as AX = B,
where A = \(\left[\begin{array}{rrr}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\)
and B = \(\left[\begin{array}{r}
11 \\
-5 \\
-3
\end{array}\right]\)
Since A is non – singular, (∵ |A|≠ 0)
∴ the given system has a unique solution given byX = A^-1B
[∵ AX = B ⇒ A^-11 (AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B ⇒ X = A^-1B]

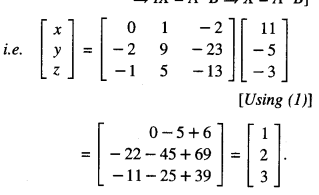
Hence, x = 1, y = 2 and z = 3.

Question 5.
If A = \(\left[\begin{array}{rrr}
3 & 1 & 2 \\
3 & 2 & -3 \\
2 & 0 & -1
\end{array}\right]\) find A^-1 the system of equations:
3x + 3y + 2z = 1
x + 2y = 4
2x – 3y – z = 5.   (C.B.S.E. Sample Paper 2018-19)
Solution:
We have A = \(\left[\begin{array}{rrr}
3 & 1 & 2 \\
3 & 2 & -3 \\
2 & 0 & -1
\end{array}\right]\)
|A| = 3[-2+0] -1 [-3+6] + 2[0-4]
= -6 – 3 – 8 = -17 ≠ 0
∴ A^-1 exits

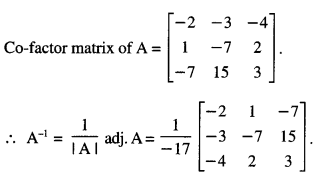
(ii) The given system of equation is

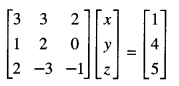
(A’)X = B
X = (A’)^-1B
X = (A^-1)^tB [ ∵ (A^t)^-1 = (A^-1)^t]

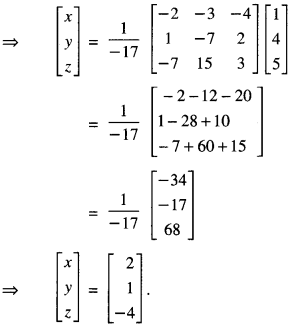
Hence x = 2, y =1, z = -4

Question 6.
If A = \(\left[\begin{array}{rrr}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right]\), find (A’)^-1 (C.B.S.E 2015)
Solution:
We have :

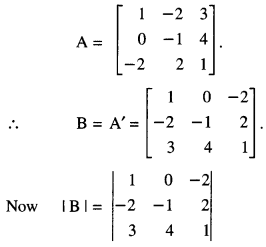
= (1)( – 1 – 8) – 0 – 2( – 8 + 3)
= – 9 + 10 = 1 ≠ 0
B^-1 exists.
Now B₁₁ = \(\left|\begin{array}{rr}
-1 & 2 \\
4 & 1
\end{array}\right|\) = – 1 – 8 = – 9;
B₁₂= \(-\left|\begin{array}{rr}
-2 & 2 \\
3 & 1
\end{array}\right|\) = – ( – 2 – 6) = 8;

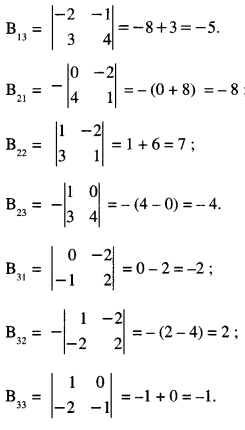
Question 7.
If A = \(\), find A^-1
Hence, solve the system of equations :
x + y + z = 6,
x + 2z = 7,
3x + y + z = 12. (C.B.S.E. 2019)
Solution:
(i) Here, A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 2 \\
3 & 1 & 1
\end{array}\right]\)
∴ |A| = 1(0-2) -(1) (1-6) + 1(1-0)
= – 2 + 5 + 1 = 4 ≠ 0
∴ A^-1 exists.

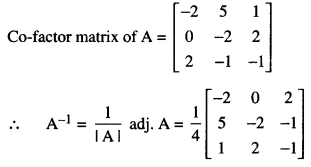
(ii) For given system of equations can be written as :

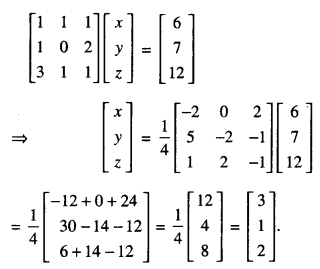
Hence x = 3, y = 1 and z = 2.

Question 8.
Find the inverse of the following matrix, using elementary operations :
A = \(\left[\begin{array}{ccc}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{array}\right]\)
Solution:
We know that A = I₃A

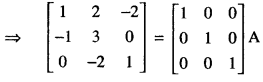
Question 9.
Using elementary transformations, find the inverse of the matrix :
A = \(\left[\begin{array}{lll}
8 & 4 & 3 \\
2 & 1 & 1 \\
1 & 2 & 2
\end{array}\right]\) and use it to solve the following system of equations:
8x + 4y + 3z = 19
2x + y + z = 5
x + 2y + 2z = 7. (C.B.S.E. 2016)
Solution:
(i) We know that AA^-1 = I

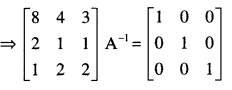
(ii) The given system of equations can be written as AX = B …(1),
Where A = \(\left[\begin{array}{lll}
8 & 4 & 3 \\
2 & 1 & 1 \\
1 & 2 & 2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{c}
19 \\
5 \\
7
\end{array}\right]\)
From AX = B
⇒ A^-1(AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B
⇒ X = A^-1B

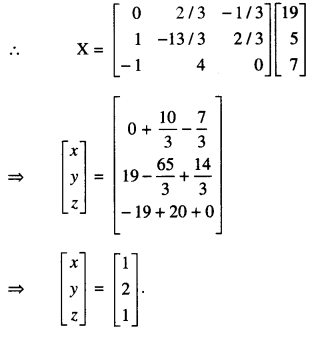
Hence x = 1, y = 2, z = 1.

Question 10.
If A = \(\left[\begin{array}{rrr}
2 & 3 & 10 \\
4 & -6 & 5 \\
6 & 9 & -20
\end{array}\right]\) , find A^-1. Using A-1 , solve the system of equations:

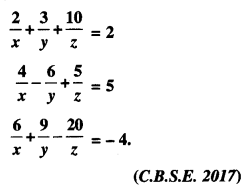
Solution:
The given system of equation is:

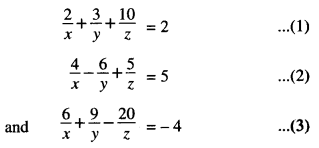
These equations can be written as:
AX = B ……….(4)

= 2(120 – 45) – 3 (- 80 – 30) + 10 (36 + 36)
= 150 + 330 + 720= 1200 ≠ 0.
∴ A is non-singular and as such A^-1 exists.


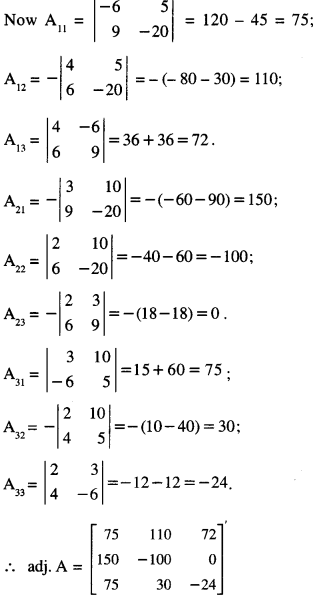
From (4)
⇒ A^-1(AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B
⇒ X = A^-1B

Hence x = 2, y = -3 and z = 5.

Question 11.
The monthly incomes of Aryan and Babban are in the ratio 3 : 4 and their monthly expenditures are in the ratio 5 : 7. If each saves ₹ 15,000 per month, find their monthly incomes, using matrix method. (C.B.S.E. 2016)
Solution:
Let ₹3x and ₹4x be the monthly income of Aryan and Babban respectively.
Let ₹5y and ₹7y be the monthly expenditure of Aryan and Babban respectively.
By the question,
3x – 5y = 15000 …(1)
and 4x – 7y = 15000 …(2)
These equations can be written as AX = B …..(3)
where A = \(\left[\begin{array}{ll}
3 & -5 \\
4 & -7
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and

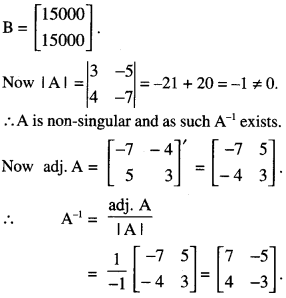
From (3),
⇒ A^-1(AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B
⇒ X = A^-1B

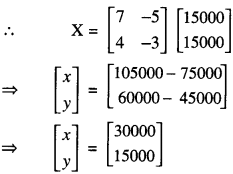
⇒ x = 30,000.
Hence,monthly income of Aryan
= 3(30,000) = ₹ 90,000
and monthly income of Babban
= 4(30,000) = ₹ 1,20,000.

Question 12.
A typist charges ₹ 145 for typing 10 English and 3 Hindi pages, while charges for typing 3 English and 10 Hindi pages are ₹180. Using matrices, And the charges of typing one English and one Hindi page separately. (A.I.C.B.S.E. 2016)
Solution:
Let ₹x and ₹y be the charges for 1 page of En¬glish and Hindi respectively.
By the question,
10x + 3y = 145 …(1)
and 3x + 10y = 180 …(2)
These can be written as AX = B …(3),
Where A = \(\left[\begin{array}{rr}
10 & 3 \\
3 & 10
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\)
and B = \(\left[\begin{array}{l}
145 \\
180
\end{array}\right]\)
now |A| = \(\left|\begin{array}{rr}
10 & 3 \\
3 & 10
\end{array}\right|\) = 100 – 9 = 91 ≠ 0
∴ A is non-singular and as such A^-1 exits.

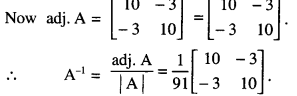
From (3)
⇒ A^-1(AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B
⇒ X = A^-1B

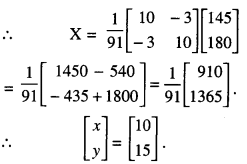
Thus x = 10 and y = 15
Hence, the charges are ₹ 10 and ₹ 15 per page of English and Hindi respectively.

Question 13.
The management committee of a residential colony decided to award some of its members (say x) for honesty, some (say y) for helping others and some others (say z) for supervising the workers to keep die colony neat and clean. The sum of all the awardees is 12. Three times the sum of the awardees for cooperation and supervision added to two times the number of awardees for honesty is 33. If the sum of the number of awardees for honesty and supervision is twice the number of awardees for helping others. Using matrix method, find the number of awardees of each category.   (A.I.C.B.S.E. 2013)
Solution:
Let x, y and z refer to honesty, co-operation and supervision respectively.
∴ x + y + z = 12 …(1)
3(y + z) + 2x = 33
i.e. 2x + 3y + 3z = 33 …(2)
and x + z = 2y
i.e. x – 2y + z = 0 …(3)
These can be written as AX = B – (4),

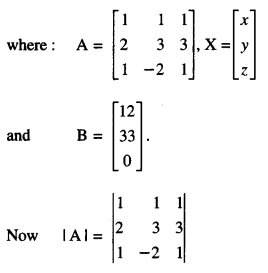
= (1) (3 + 6) – (1) (2 – 3) + (1) (-4-3)
= 9 + 1 – 7 = 3 ≠ 0.
∴ A is non-singular and as such A^-1 exists.


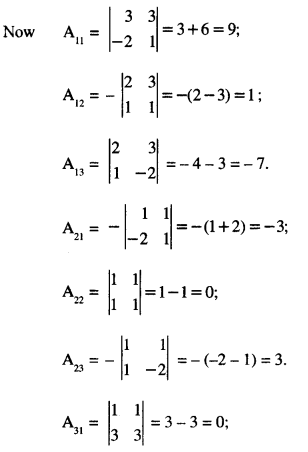
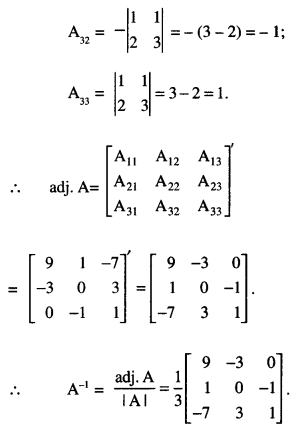
From (4)
⇒ A^-1(AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B
⇒ X = A^-1B

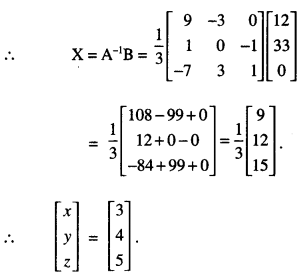
Thus, x = 3, y = 4 and z = 5.
Hence, the number of awardees are 3, 4 and 5 in three categories.