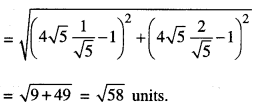Applications of Derivatives Class 12 Important Extra Questions Maths Chapter 6

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 6 Applications of Derivatives. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 6 Important Extra Questions Applications of Derivatives

Applications of Derivatives Important Extra Questions Very Short Answer Type

Question 1.
For the curve y = 5x- 2x³, if increases at the rate of 2 units/sec., find the rate of change of the slope of the curve when x = 3. (C.B.S.E. 2017)
Solution:
The given curve is y = 5x – 2x³
∴ \(\frac{d y}{d x}\) = 5 – 6x²
i.e. m = 5 – 6x²,
where ‘m’ is the slope.
∴ \(\frac{d m}{d t}\) = —12x\(\frac{d x}{d t}\) =-12x(2) = -24x
∴ \(\left.\frac{d m}{d t}\right]_{x=3}\)= -24(3) = -72.
Hence, the rate of the change of the slope = -72.

Question 2.
Without using the derivative, show that the function f(x) = 7x – 3 is a strictly increasing function in R. (N.C.E.R.T.)
Solution:
Let x₁ and x₂∈ R.
Now x₁ > x₂
⇒ 7x₁ > 7x₂
⇒ 7x₁ – 3 > 7x₂ – 3
⇒ f(x₁) > f(x₂).
Hence, ‘f ’ is strictly increasing function in R.

Question 3.
Show that function:
f(x) = 4x³ – 18×2 – 27x – 7 is always increasing in R. (C.B.S.E. 2017)
Solution:
We have :f(x) = 4x³ – 18×2 – 27x – 7
∴ f(x) = 12x² – 36x + 27 = 12(x² – 3x) + 27
= 12(x² – 3x + 9/4) + 27 – 27
= 12(x – 3/2)²∀ x∈ R.
Hence, f(x) is always increasing in R.

Question 4.
Find the slope of the tangent to the curve:
x = at²,y = 2at at t = 2.
Solution:
The given curve is x – at², y = 2at.
∴ \(\frac{d x}{d t}\) = 2at
\(\frac{d x}{d t}\)= 2a
∴ \(\frac{d y}{d x}=\frac{d y / d t}{d x / d t}=\frac{2 a}{2 a t}=\)
Hence, slope of the tangent at t = 2 is: \(\left.\frac{d y}{d x}\right]_{t=2}=\frac{1}{2}\)

Question 5.
Find the maximum and minimum values, if any, of the following functions without using derivatives:
(i) f(x) = (2x-1)² + 3
(ii) f(x)= 16x² – 16x + 28
(iii) f(x) = -|x+ 1| + 3
(iv) f(x) = sin 2x + 5
(v) f(x) = sin (sin x).
Solution:
(i) We have :
f(x) = (2x – 1)² + 3.
Here D_f = R.
Now f(x) ≥ 3.
[∵ (2x – 1)² ≥ 0 for all x ∈ R]
However, maximum value does not exist.
[∵ f(x) can be made as large as we please]

(ii) We have :
f(x) = 16x² – 16x + 28.
Here D_f = R.
Now f(x) = 16 (x² – x + \(\frac{1}{4}\) + 24
= (16(x – \(\frac{1}{2}\) )² + 24
⇒ f(x) ≥ 24.
[∵ 16(x – \(\frac{1}{2}\) )² ≥ 0 for all x ∈ R
Hence, the minimum value is 24.
However, maximum value does not exist.
[ ∵ f(x) can be made as large as we please]

(iii) We have :
f(x) = – 1x + 11 + 3
⇒ f(x) ≤ 3.
[ ∵ -|x + 1| ≤ 0]
Hence, the maximum value = 3.
However, the minimum value does not exist.
[∵ f(x) can be made as small as we please]

(iv) We have :
f(x) = sin2x + 5.
Since – 1 ≤ sin 2x ≤ 1 for all x ∈ R,
– 1+5 ≤ sin2x + 5 ≤ 1+5 for all x∈ R
⇒ 4 ≤ sin2x + 5 ≤ 6 for all x ∈ R
⇒ 4 ≤ f(x) ≤ 6 for all x ∈ R.
Hence, the maximum value = 6 and minimum value = 4.

(v) We have :
f(x) = sin (sin x).
We know that – 1 ≤ sin x ≤ 1 for all x ∈ R
⇒ sin(-1) ≤ sin(sinx) ≤ sin 1 for all x ∈ R
⇒ – sin 1 ≤ f(x) ≤ sin 1.
Hence, maximum value = sin 1 and minimum value = -sin 1.

Question 6.
A particle moves along the curve x² = 2y. At what point, ordinate increases at die same rate as abscissa increases? (C.B.S.E. Sample Paper 2019-20)
Sol. The given curve is x² = 2y …(1)
Diff.w.r.t.t, 2x\(\frac{d x}{d t}\) = 2 \(\frac{d y}{d t}\)
⇒ 2x\(\frac{d x}{d t}\) = 2 \(\frac{d x}{d t}\)
∵ \(\frac{d y}{d t}=\frac{d x}{d t}\) given
From(1), 1 = 2y ⇒ y = \(\frac{1}{2}\)
Hence, the reqd. point is (1, \(\frac{1}{2}\) )

Applications of Derivatives Important Extra Questions Long Answer Type 1

Question 1.
A ladder 13 m long is leaning against a vertical wall. The bottom of the ladder is dragged away from the wall along the ground at the rate of 2 cm/sec. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall? (C.B.S.E. Outside Delhi 2019)
Solution:
Here, \(\frac{d x}{d t}\) = 2 cm/sec.

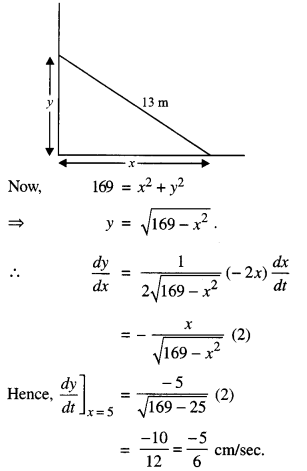
Hence, the height is decreasing at the rate of 5/6 cm/sec.

Question 2.
Find the angle of intersection of the curves x² + y² = 4 and (x – 2)² + y²= 4, at the point in the first quadrant (C.B.S.E. 2018 C)
Solution:
The given curves are :
x² + y² = 4 ………….(1)
(x – 2)² + y² = 4 ………….. (2)

From (2),
y = 4 – (x – 2)²
Putting in (1),
x² + 4-(x-2)² = 4
⇒ x² – (x – 2)² = 0
⇒ (x + x-2)(x-x + 2) = 0
⇒ (2x – 2)(2) = 0
⇒ x = 1.
Putting in (1),
1 + y² = 4
⇒ y = √3
∴ Point of intersection = (1, √3 )

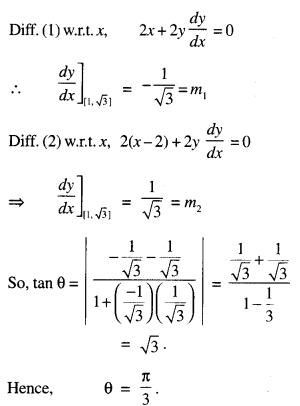
Question 3.
Find the intervals in which the function: f(x) = – 2x³ – 9x² – 12x + 1 is (i) Strictly increasing
(ii) Strictly decreasing. (C.B.S.E. 2018 C)
Solution:
Given function is:
f(x) = – 2x³ – 9x² – 12x + 1.
Diff. w.r.t. x,
f'(x) = -6x² – 18x – 12
= -6(x + 1) (x + 2).

Now, f'(x) – 0
⇒ x = -2, x = -1
⇒ Intervals are (-∞ – 2), (-2, -1) and (-1, ∞).
Getting f’ (x) > 0 in (-2, -1)
and f'(x) < 0 in (-∞, -2) u (-1, ∞)
⇒ f(x) is strictly increasing in (-2, -1) and strictly decreasing in (-∞, 2) u (-1, ∞).

Question 4.
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 metres. Find the dimensions of the window to admit maximum light through the whole opening. (C.B.S.E. 2018 C)
Solution:
Let ‘x’ and ‘y’ be the length and breadth of the rectangle ABCD.
Radius of the semi-circle = \(\frac { x }{ 2 }\) .
Circumference of the semi-circle = \(\frac{\pi x}{2}\)

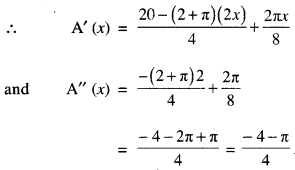
For Max ./Min. of A (x), A’ (x) = 0
\(\frac{20-(2+\pi)(2 x)}{4}+\frac{2 \pi x}{8}=0\)
20-(2 + π)(2x) + πx = 0
20 + x(π – 4 – 2π) = 0
20 – x(4 + π) = 0
x = \(\frac{20}{4+\pi}\)

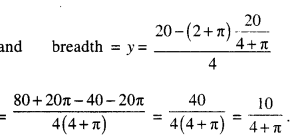
And radius of semi-circle = \(\frac{10}{4+\pi}\)

Question 5.
The length ‘x’ of a rectangle is decreasing at the rate of 3 cm/m and width ‘y’ is increasing at the rate of 2 cm/m. When x = 10 cm and y = 6 cm, find the rate of change of:
(a) the perimeter and
(b) the area of the rectangle. (N. C.E.R.T.)
Solution:
We have: \(\frac{d x}{d t}\) = -3 cm/m …(1)
and \(\frac{d y}{d t}\) = 2 cm/m …(2)

a) Perimeter, p = 2x + 2y.
∴ \(\frac{d p}{d t}=2 \frac{d x}{d t}+2 \frac{d y}{d t}\)
= 2(-3) + 2(2)
[Using (1) and (2)]
= – 6 + 4 = -2.
Hence \(\left.\frac{d p}{d t}\right]_{x=10 \atop y=6}\) = -2cm/m.

(b) Area, A = xy.
∴ \(\frac{d \mathrm{~A}}{d t}=x \frac{d y}{d t}+y \frac{d x}{d t}\) = x(2) + y(-3)
[Using (1) and (2)]
Hence \(\left.\frac{d p}{d t}\right]_{x=10 \atop y=6}\) = 10(2) + 6(-3)
= 20-18
= 2cm²/m.

Question 6.
A stone is dropped into a quiet lake and waves move in circles at a speed of 4 cm per second. At the instant when the radius of the circular wave is 10 cm, how fast is the enclosed area increasing ? (N.C.E.R.T.)
Solution:
Let ‘r’ be the radius of the circular wave.
Then A = π r², where A is the enclosed area at time t.
Differentiating w.r.t. t, we have:
\(\frac{d \mathrm{~A}}{d t}=2 \pi r \frac{d r}{d t}=2 \pi r(4)\) [∵ \(\frac{d r}{d t}\) = 4cm/s]
= 8πr.
When r = 10cm, \(\frac{d A}{d t}\)= 8K (10) = 80π cm²/s.
Hence, the enclosed area is increasing at the rate of 80π cm²/s.. when r = 10 cm.

Question 7.
Find the intervals in which the function f(x) is (i) strictly increasing (ii) strictly decreasing:
f(x) = x³ – 12x² + 36x + 17. (C.B.S.E. 2009 C)
Solution:
We have :
f(x) = x³ – 12x² + 36x + 17 – 12x² + 36x + 17.
∴ f'{x) = 3x² – 24x + 36.

(i) For f(x) to be strictly increasing function of x: f'(x) > 0
⇒ 3x² – 24x + 36 > 0
⇒ x² – 8x+ 12 > 0
⇒ (x – 2) (x – 6) > 0
⇒ x < 2 or x > 6.
Hence, f(x) is increasing in the interval (-∞ 2) ∪ (6, ∞).

(ii) For f (x) to be strictly decreasing function of x:
f'(x) <0 ⇒  3x² – 24x + 36 < 0 ⇒ x² – 8x + 12 < 0 ⇒ (x – 2) (x – 6) < 0 ⇒ 2 < x < 6.
Hence, f(x) is decreasing in the interval (2,6).

Question 8.
Find the intervals in which the function :
f(x) = 3x⁴ – 4x³ – 12x² + 5 is:
(a) strictly increasing
(b) strictly decreasing. (C.B.S.E. 2014)
Solution:
We have: f(x) = 3x⁴ – 4x³ – 12x² + 5.
∴ f'(x) = 12x³ – 12x² – 24x
= 12x(x² – x – 2)
= 12x(x – 2)(x + 1).
When x < – 1.
f”(x) = 12 (-ve) (-ve) (-ve) = -ve.
Thus f(x) is strictly decreasing.
When -1 < x < 0.
f'(x) = 12(-ve)(-ve)(+ve) = +ve.
Thus f(x) is strictly increasing.

When 0 < x < 2. f'(x) = 12(+ve)(-ve)(+ve)=-ve. Thus f(x) is strictly decreasing. When x > 2.
f'(x) – 12(+ve)(+ve)(+ve) = +ve.
Thus f(x) is strictly increasing.
Combining,/(x) is
0a) strictly increasing in (-1,0) u (2, ∞) and
(b) strictly decreasing in (-∞, -1) u (0,2).

Question 9.
Find the point at which the tangent to the curve
y = \(\sqrt{4 x-3}\) 1 has its slope \(\frac{2}{3}\) (N.C.E.R.T.)
Solution:
The given curve is :

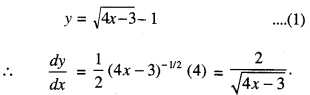
By the question,
slope = \(\frac{2}{3}\)
\(\frac{2}{\sqrt{4 x-3}}=\frac{2}{3}\)
⇒ \(\sqrt{4 x-3}\) = 3.
Squaring, 4x – 3 = 9
⇒ 4x = 12
⇒ x = 3.
Putting in (1),
y = \(\sqrt{4(3)-3}=\sqrt{9}-1\)
= 3-1 = 2.
Hence, the reqd. point is (3,2).

Question 10.
Find the equations of all lines having slope 2 and being tangents to the curve:
\(y+\frac{2}{x-3}=0\) (N.C.E.R.T)
Solution:
The given curve is y + \(y+\frac{2}{x-3}=0\) = 0
y = \(-\frac{2}{x-3}\)
∴ \(\frac{d y}{d x}=\frac{2}{(x-3)^{2}}\)
By the question, \(\frac{2}{(x-3)^{2}}\) = 2
⇒ (x-3)² = 1
x – 3 = ± 1
⇒ x = 2, 4.

When x = 2, then from (1),
y = \(\frac{-2}{2-3}=\frac{-2}{-1}\)
= 2.
When x = 4, then from (1),
y = \(\frac{-2}{4-3}=\frac{-2}{1}\) = 2

Thus there are two tangents to the given curve with slope 2 and passing through (2, 2) and (4,-2).
∴ The equation of the tangent through (2,2) is: y-2 = 2(x-2)
⇒ y-2x + 2 = 0
and the equation of the tangent through (4,-2) is:
y-(-2) = 2(x-4)
⇒ y-2x+ 10 = 0.

Question 11.
Find the equation of the tangent to the curve y = \(\sqrt{3 x-2}\) which is parallel to the line 4x – 2y + 5 = 0. Also, write the equation of normal to the curve at the point of contact.
(C.B.S.E. 2019)
Solution:
(i) The given curve is y = \(\sqrt{3 x-2}\) …(1)
∴ Slope of the tangent, \(\frac{d y}{d x}=\frac{3}{2 \sqrt{3 x-2}}\)
Slope of the given line 4x – 2y + 5 = 0 is \(-\frac{4}{-2}\) = 2
Since the tangent is parellel to (2)
∴ \(\frac{3}{2 \sqrt{3 x-2}}\) = 2 (∵ m₁ = m₂)
3 = 4\(\sqrt{3 x-2}\)
9 = 16(3x – 2)
= 48x = 41
x = \(\frac{41}{48}\)

⇒ 6(4y-3) = 48x-41
⇒ 48x-24y = 23.

(ii) Slope of normal x Slope of tangent = – 1
⇒ Slope of normal = – 1/2
∴ The equation of the normal is :
\(y-\frac{3}{4}=-\frac{1}{2}\left(x-\frac{41}{48}\right)\)

Question 12.
Find the equations of the tangent and the normal to the curve 16x² + 9y² = 145 at the point (x₁, x₂ where x₁ = 2 and y₁ > 0. (C.B.S.E. 2018)
Solution:
The given curve is :
16x² + 9y² = 145 …(1)
Since (x_1s, y₁,) lies on (1),
.-. 16x²+9y] = 145
⇒ 16(2)² + 9y₁² = 145
⇒ 9y₁² = 145-64
⇒ 9y₁² = 81
⇒ y₁² =9
y₁ = 3 [∵ y₁ > 0]
Thus, the point is (2, 3).
Diff (1) w.r.t x ,

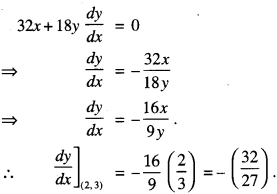
(i) The equation of tangent is :
y – 3 = \(\frac{-32}{27}\) (x-2)
⇒ 27y – 81 = -32x + 64
⇒ 32x + 27y = 145

(ii) The equation of normal is :
y – 3 = \(\frac{27}{32}\)(x – 2)
⇒ 32y – 96 = 27x – 54
⇒ 27x – 32y + 42 =0.

Question 13.
Find the equations ofthe tangent and normal to the curve given by:
x = a sin³ θ, y = a cos³θ at a point, where θ = \(\frac{\pi}{4}\) (1C.B.S.E. 2014)
Solution:
The given curve is:
x = a sin³ θ, y = a cos³θ

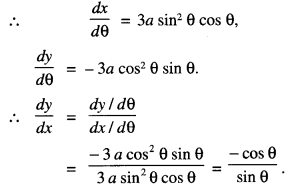
∴ Slope of the tangent at θ = \(\frac{\pi}{4}\)

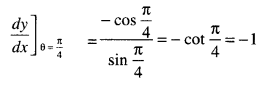
and slope of the normal = 1.
When θ = \(\frac{\pi}{4}\), then from (1),

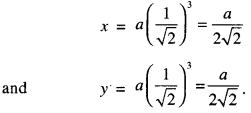
∴ The equations of the tangent and normal to (1) at θ = \(\frac{\pi}{4}\) are :

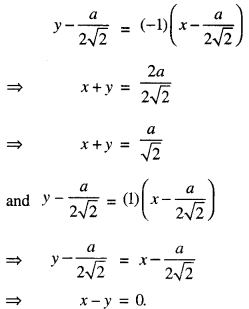
Question 14.
Find the equation of the tangent to the curve
ay² = x³ at the point (am², am³) (C.B.S.E. 2019 C)
Solution:
The given curve is ay² = x³
y = a^-1/23/2

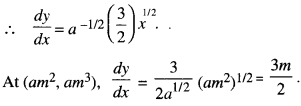
∴ The equation of the tangent is:
y – y’ = \(\frac{d y}{d x}\) (x – x’)
y – am³ = \(\frac{3 m}{2}\)(x – am²)
2y – 2 am³ = 3 mx – 3 am³
3mx – 2y = am³.

Question 15.
Find the equation of the tangent to the curve x² + 3y = 3, which is parallel to the line y – 4x + 5 = 0. (C.B.S.E. 2009 C)
Solution:
The given curve is x² + 3y = 3
y = \(\frac{1}{3}\) (3 – x²
∴ \(\frac{d y}{d x}=\frac{1}{3}(0-2 x)=-\frac{2}{3} x\)
which is the slope of the tangent.
But the tangent is parallel to the line
y – 4x + 5 = 0, whose slope is 4.
Thus \(-\frac{2}{3}\)x = 4 [∵ m₁ = m₂]
⇒ x = -6.
From(l), y = \(\frac{1}{3}\) (3 – 36) = -11.
Thus the point of contact is (- 6, – 11).
The equation of the tangent is :
y + 11 = 4(x + 6)
⇒ y + 11 = 4x + 24
⇒ 4x – y+ 13 = 0.

Question 16.
Find the equations of the normal to the curve y = 4x³ – 3x + 5, which are perpendicular to the line 9x – y + 5 = 0.
(C.B.S.E. Sample Paper 2018-19)
Solution:
The given curve is :
y = 4x² – 3x + 5.
Let the required normal be at (x₁ y₁,).
Slope of the tangent = \(\frac{d y}{d x}\) = 12x² – 3.
m₁ = slope of the normal

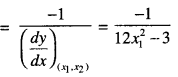
and m₂ = Slope of the line = 9.
Since, the normal is perpendicular to the lines
m₁ m₂ = -1
\(\frac{-1}{12 x_{1}^{2}-3} \times 9\) = -1
12x₁² = 9
x₁² = 1
x₁ = ±1.

When x₁ = 1, then y₁ = 4-3 + 5 = 6.
When x₁ = -1, then y₁ = -4 + 3 + 5 = 4.
Thus the points are (1, 6) and (-1,4).
∴ The equations of the normal are :
y – 6 = \(-\frac { 1 }{ 9 }\) (x-1) i.e.,x + 9y = 55
and y – 4= \(-\frac { 1 }{ 9 }\) (x+ 1) i.e.,x + 9y = 35.

Question 17.
Using differentials, find the approximate value of \(\sqrt[3]{0.026}\) , upto three places of decimals.
Solution:
Let y = f(x) = x^1/3
Take x = 0.027,
x + Δx = 0.026
Δx = 0.026 – 0.027 = -0.001.
x = 0.027,
y = \(\sqrt[3]{0 \cdot 027}\) =0.3.
Let dx = Δx = -0.001.

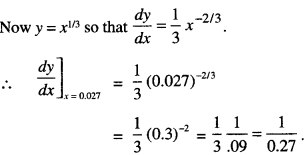
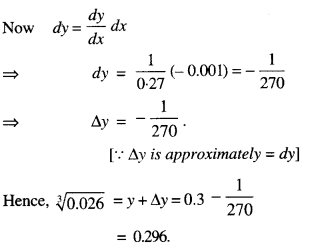
Question 18.
If the radius of a sphere is measured as 9 m with an error of 0.03 m, then find the approximate error in calculating its surface area. (N.C.E.R.T.; A.I.C.B.S.E. 2011)
Solution:
Let ‘r’ be the radius of the sphere and Ar be the error in measuring the radius.
Then r = 9m and Δr = 0.03 m.
Now S, the surface area of the sphere is given by:
S = 4πr²
∴ \(\left(\frac{d S}{d r}\right)\) = 8πr
Now dS = \(\left(\frac{d S}{d r}\right)\)Δr = (8πr)Δr
= (8π)(9))(0.03) = 2.16πm²
Hence, the approximate error in calculating the surface area is 2.16πm²

Question 19.
Find the absolute maximum and the absolute minimum value of the function given by:
f(x) = sin²x – cos x, x ∈ [0, π]. (A.I.C.B.S.E. 2015)
Solution:
We have :
f(x) = sin²x – cos x.
∴ f'(x) – 2 sin x cos x + sin x
= sinx(2cosx+ 1).
Now f'(x) 0
⇒ sin x (2 cos x + 1) = 0
⇒ sin x = 0 or cosx = \(-\frac{1}{2}\)
x = 0, π or x = \(\frac{2 \pi}{3}\)
Now f(0) = 0 – 1 = -1

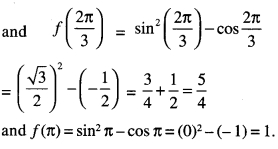
Hence, absolute maximum value is \(\frac{5}{4}\) and absolute minimum values is – 1.

Question 20.
Find all the points of local maxima and local minima of the function ‘f’ given by: f(x) = 2x³ – 6x² + 6x + 5. (N.C.E.R.T.)
We have: f(x) = 2x³ – 6x² + 6x + 5.
f'(x) = 6x² – 12x + 6 = 6(x – 1)².
f”(x) = 12 (x – 1).
Now f'(x) = 0 gives x = 1.
Also, f”(1) = 0.
Thus x = 1 is neither a point of maxima nor of minima
Now f” (x) = 12.
And f'”(x)]_x=1 = 1 = 12 ≠ 0.
Hence, x = 1 is a point of inflexion.

Applications of Derivatives Important Extra Questions Long Answer Type 2

Question 1.
Water is leaking from a conical funnel at the rate of 5 cm Vs. If the radius of the base of funnel is 5 cm and height 10 cm, find the rate at which the water level is dropping when it is 2.5 cm from the top.
Solution:
Here 5 cm is the radius and 10 cm is the height of the conical funnel.
Let ‘r’ be the radius of the base and ‘h’ the height at any stage.

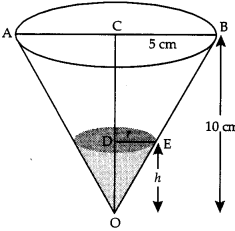
∴ V, volume of water in conical funnel
= \(\frac{1}{3}\) πr²h …………. (1)
Now Δs OBC and OED are similar

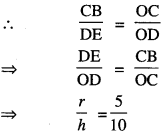
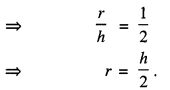
∴ From (1), V, volume of water in conical funnel

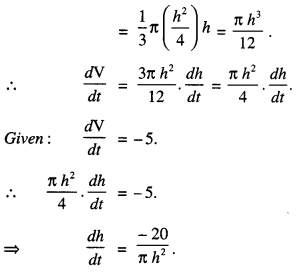
When the water level is 2.5 cm from the top, then
h = 10 – 2.5 = 7.5 cm.

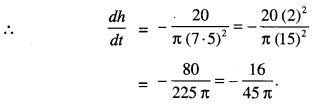
Hence, the rate at which the water level is 16 .
dropping is \(\frac{16}{45 \pi}\) cm/s.

Question 2.
A man is moving away from a tower 41.6 m high at the rate of 2 m/s. Find the rate at which the angle of elevation of the top of tower is changing when he is at a distance of 30 m from the foot of the tower. Assume that the eye level of the man is 1.6 m from the ground.
Solution:
Let AB (= 41.6 m) be the tower.
Let the man be at a distance of ‘x’ metres from the tower AB at any time t. If ‘0’ be the angle of elevation at time t, then :

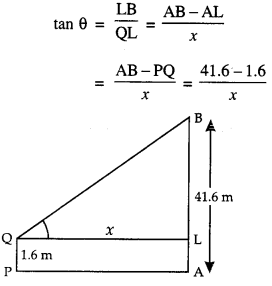
⇒ tan θ = \(\frac { 40 }{ x }\)
⇒ x = 40 cot θ …………. (1)
\(\frac{d x}{d t}\) = -40 cosec² θ. \(\frac{d \theta}{d t}\)
⇒ 2 = -40 cosec².θ\(\frac{d \theta}{d t}\) [∵ \(\frac{d x}{d t}\) = 2(given) ]

When x = 30, then from (1),
30 = 40 cot θ
⇒ cot θ = \(\frac{3}{4}\)
so that cosec² θ = 1+ cot\frac{3}{4} = 1 + \(\frac{9}{16}=\frac{25}{16}\)
Putting in (2),

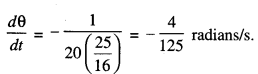
Hence, the angle of elevation of the top of the
tower is reducing at the rate of \(\frac{4}{125}\) radians/s.

Question 3.
Find the intervals in which:
f(x) = sin 3x – cos 3r, 0 < x < π, is strictly increasing or strictly decreasing. (C.B.S.E. 2016)
Solution:
We have : f'(x) = sin 3x – cos 3x.
f'(x) = 3 cos 3x + 3 sin 3x.
Now f(‘x) = 0
⇒ 3 cos 3x + 3 sin 3x = 0
⇒ cos 3x = – sin 3x
⇒ tan 3x = – 1

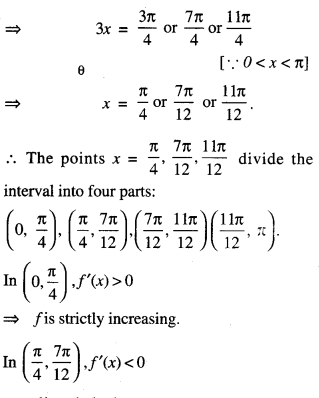
⇒ f is strictly decreasing.
In \(\left(0, \frac{\pi}{4}\right), f^{\prime}(x)\) < 0 f is strictly increasing. ⇒ f is strictly decreasing. In \(\left(\frac{7 \pi}{12}, \frac{11 \pi}{12}\right)\)f'(x) >0
⇒ f is strictly increasing.
In \(\left(\frac{11 \pi}{12}, \pi\right)\), f'(x) < 0
⇒ f is strictly decreasing.
Hence, ‘f’ is strictly increasing in

Question 4.
Show that the equation of normal at any point ‘t’ on the curve:
x = 3 cos t – cos³t and y = 3 sin t – sin³t is : 4(y cos³ t-x sin³t) = 3 sin 4t. (C.B.S.E. 2016)
Solution:
The given curve is :
x = 3 cos t – cos³t and y = 3 sin t – sin³t.
\(\) = -3 sin t – 3 cos²t (- sin t)
= -3 sin t (1- cos²t)
= -3 sin t sin² t
= -3 sin³t
and \(\frac{d y}{d t}\) = 3 cos t – 3 sin²t cos t
= 3 cos t (1- sin²t)
= 3 cos t cos² t = 3 cos² t.
= \(\frac{3 \cos ^{3} t}{-3 \sin ^{3} t}=-\frac{\cos ^{3} t}{\sin ^{3} t}\)
∴ Slope of normal = \(\frac{\sin ^{3} t}{\cos ^{3} t}\)
∴ The equation of the normal at ‘t’ is: y – (3 sin t – sin³ t)
= \(\frac{\sin ^{3} t}{\cos ^{3} t}\)(x – 3 cos t + cos³ t)
⇒ y cos³ t – 3 sin t cos³ t + sin³ t cos³ t
⇒ x sin³ t – 3 cos t sin³ t + sin³ t cos³ t
⇒ y cos³ t – x sin³t
= 3 sin t cos t (cos³t – sin³t)
⇒ y cos³ t – x sin³ t = \(\frac{3 \sin 2 t \cos 2 t}{2}\)
⇒ y cos³ t – x sin³ t = \(\frac{3}{4}\) sin 4t
⇒ 4(y cos³ t – x sin³ t) = 3 sin 4t, which is true.

Question 5.
A cuboidal shaped godown with square base is to be constructed. Three times as much cost per square metre is incurred for constructing the roof as compared to the walls. Find the dimensions of the godown if it is to enclose a given volume and minimize the cost of constructing the roof and the walls.
(C.B.S.E. Sample Paper 2018-19 C)
Solution:
Let the length and breadth of the base = x and the height of the godown = y.
If C be the cost of construction and V, the volume.
∴ C = k[3x² + 4xy] …(1),
where k > 0 is constant of proportionality
⇒ x2y = V (constant) …(2)
⇒ y = \(\frac{\mathrm{V}}{x^{2}}\) …………. (3)
Putting the value of y from (3) in (1), we get:

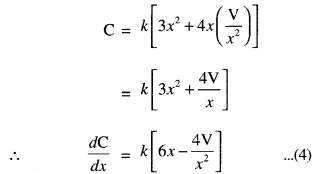
Question 6.
A given quantity of metal is to be cast into a solid half circular cylinder (i.e., with rectangular base and semi-circular ends). Show that in order that the total surface area may be minimum, the ratio of the length of the cylinder to the diameter of its circular ends is π: (π + 2). (C.B.S.E. Sample Paper 2019-20)
Solution:
Let ‘r’ be the radius and ‘h’, the height of the cylinder.
∴ V = Volume of half cylinder = \(\frac { 1 }{ 2 }\) πr²h …….(1)

Total surface area, S = S₁ (Surface area of semi¬circular ends) + S₂ (Curved surface of half cylinder) + S₃ (Surface area of rectangular base having height h and width 2r)
( \(\frac { 1 }{ 2 }\)πr² \(\frac { 1 }{ 2 }\)πr²) + \(\frac { 1 }{ 2 }\)(2πrh) + 2rh
= πr² + πrh + 2rh
= πr² + (π + 2)r\(\frac{2 \mathrm{~V}}{\pi r^{2}}\)
[Using (1)]
∴ S = πr² + \(\frac{2 \mathrm{~V}}{\pi r}\) (π+2) ……. (2)
∴ \(\frac{d \mathrm{~S}}{d r}=2 \pi r-\frac{2 \mathrm{~V}}{\pi r^{2}}(\pi+2)\)

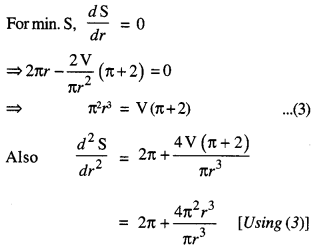
= 2π + 4π = 6π
which is +ve
∴ S is minimum when π²r³ = V(π + 2)
π²r³ = \(\frac { 1 }{ 2 }\)πr²(π + 2)
\(\frac{h}{2 r}=\frac{\pi}{\pi+2}\)
Hence, h:2r = π: {π + 2), which is true.

Question 7.
A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If the building of tank costs ₹70 per sq. metre for the base and ₹45 per sq. metre for the sides, what is the cost of least expensive tank? (C.B.S.E. 2019)
Solution:
Let ‘x’ and ‘y’ be the length and breadth respetively of the tank.
And depth of the tank = 2 m.
∴ Volume of the tank = 2xy.

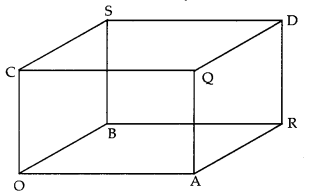
By the question,
2xy = 8
⇒ xy = 4 …(1)
Nowarea of the base = xy
and area of the sides = 2 (x + y) (2) = 4 (x + y)
∴ Cost of construction
= ₹(70xy+ 45 (4(x + y)) …(2)
= ₹(70xy+ 1800 + y))
∴ C, the cost of construction
= 70 (4) +180( x + \(\frac{4}{x}\)) [Using (1)]
= 280 + 180 ( x + \(\frac{4}{x}\))
∴ \(\frac{d \mathrm{C}}{d x}=180\left(1-\frac{4}{x^{2}}\right)=180\left(\frac{x^{2}-4}{x^{2}}\right)\)

For max ./min.,
\(\frac{d \mathrm{C}}{d x}\) = 0
x² – 4 = 0
x = ±2.
x = 2. [∵ Length can’t be -ve]

From(1), y = \(\frac{4}{2},\) = 2.
Thus the tank is a cube of side 2 m.
∴ Least cost of construction
= ₹[280 + 180(2 + \(\frac{4}{2},\) )] [From (3)]
= ₹ (280 + 720) = ₹1000. [From (3)]

Question 8.
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quanity of water. Show that the cost of the material will be least when the depth of the tank is half of its width. (C.B.S.E. 2018)
Solution:
Let ‘x’ be the side of the square base and V the depth of the tank.
Now, V = x²y …(1)
Now S, surface area = x² + 4xy
∴ C, cost is proportional to surface area = k(x² + 4xy)

Hence, the cost of material least when depth is half of its width.

Question 9.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius ‘r’ is \(\frac { 4r }{ 2 }\). Also find the maximum volume of the cone.
(C.B.S.E. 2019 (Delhi))
Solution:
(i) Let ‘x’ be the distance of the base BC from the centre O of the sphere.

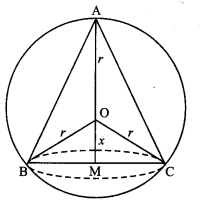
∴ Height of the cone = AM = r + x
andradius of the base = BM = \(\sqrt{r^{2}-x^{2}}\).
∴ V, the volume of the cone
= \(\frac{1}{3}\)π(r² – x2)(r+x).
∴ \(\frac{d \mathrm{~V}}{d x}\)= \(\frac{1}{3}\)π(r² – x²) + \(\frac{1}{3}\)π( – 2x)(r + x)
= \(\frac{\pi}{3}\)(r + x)(r – x – 2x)
= \(\frac{\pi}{3}\)(r + x)(r – 3x)
and \(\frac{d^{2} V}{d x^{2}}\) = \(\frac{\pi}{3}\)(r + x)( – 3) + \(\frac{\pi}{3}\)(1) (r – 3x)
= \(\frac{\pi}{3}\)( – 3r – 3x + r – 3x)
= \(\frac{\pi}{3}\)( – 2r – 6x).
For V to be max, \(\frac{d \mathrm{~V}}{d x}\) = 0 and \(\frac{d^{2} \mathrm{~V}}{d x^{2}}\) < 0
Now \(\frac{d \mathrm{~V}}{d x}\) = 0 gives :
\(\frac{\pi}{3}\) (r + x )(r – 3x) = 0
⇒ x = -r, \(\frac{r}{3}\)
but x ≠ -r
x = \(\frac{r}{3}\)
Also \(\left.\frac{d^{2} \mathrm{~V}}{d x^{2}}\right]_{x=\frac{r}{3}}=\frac{\pi}{3}(-2 r-2 r)=-\frac{4}{3} \pi r\)
Which is -ve
Hence, V is max. when x = \(\frac{r}{3}\) i.e., when altitude
r +x = r + \(\frac{r}{3}\) = \(\frac{4r}{3}\)

(ii) Maximum volume of the cone

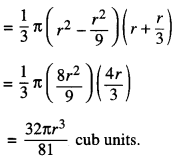
Question 10.
If the lengths ofthree sides ofa trapezium other than base are equal to 10 cm, then find the area of the trapezium when it is maximum. (N.C.E.R.T.; A.I.C.B.S.E. 2010)
Solution:

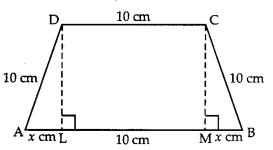
Let ABCD be the trapezium such that:
AD = BC = CD = 10 cm.
Draw DL and CM perpendiculars on AB.
Let AL = x cm.
Now ΔALD ≅ Δ BMC.
∴ MB = AL = x cm.
Also LM = 10 cm.
And DL = CM = \(\sqrt{100-x^{2}}\)
Let ‘A’ be the area of the trapezium.
Then A (x) = 1/2 (10 + (10 + 2x)) \(\sqrt{100-x^{2}}\)
[Area of Trap. = \(\frac{1}{2}\) (sum of II sides) {height))
= \(\frac{1}{2}\)(2x + 20) \(\sqrt{100-x^{2}}\)
= (x + 10) \(\sqrt{100-x^{2}}\) ………(1)
A'(x) = (x + 10)

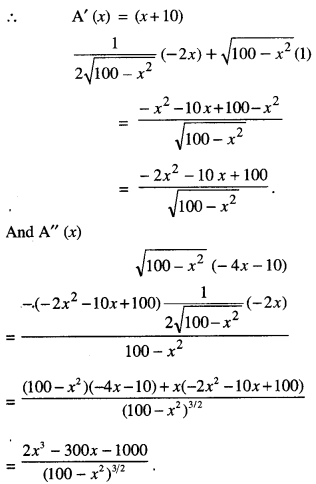
Now A'(0) = 0
⇒ -2x² – 10A+ 100 = 0
⇒ x² + 5x – 50 = 0
= (x+ 10) (x-5) = 0
=» x = -10,5.
But x ≠ – 10.
[ ∵ x, being the distance, can’t be – ve]
Thus A = 5 cm.
And

Thus A (A) is maximum when x = 5.
Hence, A (5) = (5 +10) \(\sqrt{100-25}\)
[Using (1)]
= 15√75 = 75√3 cm².

Question 11.
A metal box with a square base and vertical sides is to contain 1024 cm³. The material for the top and bottom costs₹ 5 per cm² and the material for the sides costs ₹ 2.50 per cm² Find the least cost of the box. (C.B.S.E 2017)
Solution:
Let ‘x’ cm be the side of square base and ‘y’ cm the height.
∴ volume of the box = x x x x y = x²y.
By the question,
x²y = 1024 …(1)
Now the cost, C = 5(x²) + \(\frac { 5 }{ 2 }\) (4xy)
= 5x²+ 10xy
= 5x² + 10x (\(\frac{1024}{x^{2}}\)) …………(2) [Using (1)]

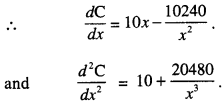
Now for least cost, \(\frac{d \mathrm{C}}{d x}\) = 0
⇒ 10x – \(\frac{10240}{x^{2}}\) = 0
⇒x³ = (1024)^1/3
⇒ x = (1024)^1/3
And \(\frac{d^{2} \mathrm{C}}{d x^{2}}\) > 0 for x = (1024)^1/3
Hence, least cost =5 (1024)^2/3 + \(\frac{10240}{(1024)^{1 / 3}}\)
= 5(1024)^2/3 + 10(1024)^2/3
= ₹ 15(1024)^2/3

Question 12.
Show that the height of the cylinder, open at the top, of given surface area and greatest volume is equal to the radius of its base. (C.B.S.E. 2010, 2019 C)
Solution:
Let ‘r’ and ‘h’ be the radius and height respectively of the cylinder.
∴ S, the surface area = πr² + 2πrh
h = \(\frac{\mathrm{S}-\pi r^{2}}{2 \pi r}\) …………(1)
And V, the volume = πr²h
i.e. V = πr² \(\left(\frac{\mathrm{S}-\pi r^{2}}{2 \pi r}\right)\) [Using(1)]
V = \(\frac{r}{2}\) (S – πr²)
V = \(\frac{1}{2}\)(Sr – πr³)
∴ \(\frac{d \mathrm{~V}}{d r}\) = \(\frac{r}{2}\) (S – 3πr²) …….. (2)
and \(\frac{d^{2} \mathrm{~V}}{d r^{2}}=-\frac{3 \pi}{2}\) (2r) = -3 πr ………(3)
For greatest volume , \(\frac{d \mathrm{~V}}{d r}\) = 0 and \(\frac{d^{2} \mathrm{~V}}{d r^{2}}\) < 0
Now \(\frac{d \mathrm{~V}}{d r}\) = 0
= \(\frac{r}{2}\) (S – 3πr²) = 0
S = 3πr²

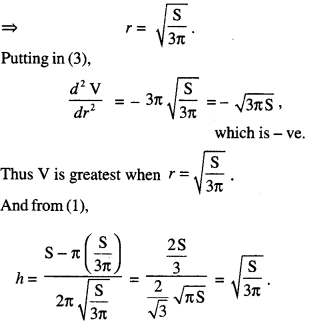
Hence, height = radius of the base.

Question 13.
An Apache helicopter of enemy is flying along the curve given by: y = x² + 7.
A soldier, placed at (3,7), wants to shoot down the helicopter when it is nearest to him. Find the nearest distance.
(NCERT; C.B.S.E. 2019 C)
Solution:
Let P (x, x² + 7) be the position of the helicopter at any instant.
Also A is (3,7).

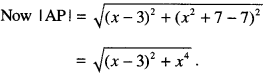
Let f(x) = (x – 3)² + x⁴.
f'(x) = 2(x-3) + 4x³ = 4x³ + 2x – 6
= 2(2x³ + x – 3) = 2(x – 1)(2x² + 2x + 3).
Now f'(x) = 0
x – 1 = 0, or 2x² + 2x+3 = 0
⇒ x = 1.
[∵ Roots of 2x² + 2x + 3 = 0 are not real] Thus, there is only one point x = 1.
And f(1) = (1 -3)²+ 14 = 4 + 1 = 5.
∴ Distance between soldier and helicopter is √5
Now √5 is either max. value or min. value.
Since \(\sqrt{f(0)}=\sqrt{(0-3)^{2}+(0)^{4}}=3>\sqrt{5}\)
⇒ √5 is min. value of \(\sqrt{f(x)}\).
Hence, √5 is the reqd. minimum distance between the soldier and the helicopter.

Question 14.
Show that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle. (C.B.S.E. Sample Paper 2019-20)
Solution:
Let O be the centre and V, the radius of the circle in which AABC is inscribed.

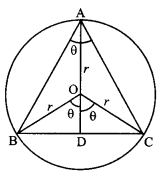
For maximum area, the vertex A should be at a maximum distance from the base BC
⇒ A must lie on the diameter, which is perp. to BC
⇒ ΔABC is isosceles.
Let ∠BAC = θ. Then ∠BOC = 2θ
⇒ DOC = θ.
Now BC = 2DC = 2OC sin θ = 2rsine…(1)
and AD = AO + OD = AO + OC cos θ
= r + r cos θ = r (1 + cos θ) …(2)
If ‘A’ be the area of the triangle, then:
A = \(\frac { 1 }{ 2 }\) (BC) (AD) = \(\frac { 1 }{ 2 }\) (2r sin θ) r (1 + cos θ)
[Using (1) & (2)]
⇒ A = r² (sin θ + sin θ cos θ).
= r²(cos θ + cos² θ – sin² θ)
= r² (cos²θ + cos θ) = r² (2cos² θ -1 + cos θ)
= r² (2cos ²θ + cos θ – 1) …………. (3)
and \(\frac{d^{2} \mathrm{~A}}{d \theta^{2}}\) = r²(4cox θ sin θ – sin θ) ……(4)
For ‘A’ to be maximum \(\frac{d \mathrm{~A}}{d \theta}\) = 0 and \(\frac{d^{2} \mathrm{~A}}{d \theta^{2}}\) < 0
Now, \(\frac{d \mathrm{~A}}{d \theta}\) = 0
⇒ r² (2 cos² θ + cos θ – 1) = 0
⇒ 2 cos² θ + cos θ – 1 = 0
⇒ (2 cos θ -1) (cos θ + 1) = 0

Thus, A is maximum when θ = \(\frac{\pi}{3}\)
But ΔABC is isosceles.
Hence, for maximum area, triangle is equilateral.

Question 15.
Find the point on the circle x² + y² = 80, which is nearest to the point (1,2). (C.B.S.E. 2019)
Solution:
Let P (√80 cos θ, √80 sin θ)
i.e. (4√5 cosθ, 4√5 sin θ) be a point on the circle x² + y² = 80.
And, A(1, 2) is the given point.
|AP| = \(\sqrt{(4 \sqrt{5} \cos \theta-1)^{2}+(4 \sqrt{5} \sin \theta-2)^{2}}\) ………….. (1)
AP is least⇒ AP² is least
D = AP² = (4√5cos θ – 1)
(4√5 sinθ – 2)² …………. (2)
\(\frac{d D}{d \theta}\)= 2(4√5 cos θ – 1)(- 4√5sin θ)
+ 2 (4θ5sin θ – 2)(4θ5cos θ)
= – 160 sin θ cos θ + 8√5 sin θ + 160 sin θ cos θ – 16√5 cos θ ………… (3)
= 8√5 (sin θ-2 cos θ) ………… (3)
and \(\frac{d^{2} \mathrm{D}}{d \theta^{2}}\) = 8√5 (cos θ + 2 sin θ) …(4)
Now \(\frac{d \mathrm{D}}{d \theta}\) = 0
⇒ 8√5(sin θ – 2 cos θ) = 0
⇒ sin θ – 2 cos θ = 0 tan θ = 2

Thus, D is least when tan θ = 2
Hence, from (1), least distance