Differential Equations Class 12 Important Extra Questions Maths Chapter 9

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 9 Differential Equations. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 9 Important Extra Questions Differential Equations

Differential Equations Important Extra Questions Very Short Answer Type

Question 1.
Find the order and the degree of the differential equation: \(x^{2} \frac{d^{2} y}{d x^{2}}=\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{4}\)
(Delhi 2019)
Solution:
Here, order = 2 and degree = 1.

Question 2
Determine the order and the degree of the differential equation:\(\left(\frac{d y}{d x}\right)^{3}+2 y \frac{d^{2} y}{d x^{2}}=0\) (C.B.S.E. 2019 C)
Solution:
Order = 2 and Degree = 1.

Question 3.
Form the differential equation representing the family of curves: y = b (x + a), where « and b are arbitrary constants. (C.B.S.E. 2019 C)
Solution:
Wehave:y= b(x + a) …(1)
Diff. w.r.t. x, b.
Again diff. w.r.t. x, \(\frac{d^{2} y}{d x^{2}}\) = 0,
which is the reqd. differential equation.

Question 4.
Write the general solution of differential equation:
\(\frac{d y}{d x}\) = e^x+y (C.B.S.E. Sample Paper 2019-20)
Solution:
We have: \(\frac{d y}{d x}\) = e^x+y
⇒ e^-y dy = e^x dx [Variables Separable
Integrating, \(\int e^{-y} d y+c=\int e^{x} d x\)
⇒ – e^-y + c = e^x
⇒ e^x + e^-y = c.

Question 5.
Find the integrating factor of the differential equation:
y\(\frac{d y}{d x}\) – 2x = y³e^-y
Solution:
The given equation can be written as.

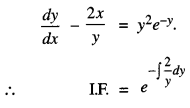
Question 6.
Form the differential equation representing the family of curves y = a sin (3x – b), where a and b are arbitrary constants. (C.B.S.E. 2019C)
Solution:
We have: y – a sin (3x – b) …(1)
Diff. W.r.t y \(\frac{d y}{d x}\) = a cos (3x – b) .3
= 3a cos (3x – b)
\(\frac{d^{2} y}{d x^{2}}\) = -3a sin (3x – b) 3
= -9a sin (3x – b)
= -9y [Using (1)]
\(\frac{d^{2} y}{d x^{2}}\) + 9y = 0,m
which in the reqd. differential equation.

Differential Equations Important Extra Questions Short Answer Type

Question 1.
Determine the order and the degree of the differential equation:
\(\left(\frac{d y}{d x}\right)^{3}+2 y \frac{d^{2} y}{d x^{2}}=0\) (Outside Delhi 2019C)
Solution:
Order = 2 and Degree = 1.

Question 2.
Form the differential equation representing the family of curves: y = e^2x (a + bx), where ‘a’ and ‘h’ are arbitray constants. (Delhi 2019)
Solution:
We have : y = e^2x (a + bx) …(1)
Diff. w.r.t. x, \(\frac{d y}{d x}\) = e^2x (b) + 2e2x (a + bx)
⇒ \(\frac{d y}{d x}\) = be^2x + 2y ………….. (2)
Again diff. w.r.t. x,
\(\frac{d^{2} y}{d x^{2}}\) = 2be^2x + 2^2x
\(\frac{d^{2} y}{d x^{2}}\) = 2(\(\frac{d y}{d x}\) – 2y) + \(\frac{d y}{d x}\)
[Using (2)]
Hence, \(\frac{d^{2} y}{d x^{2}}\) -4 \(\frac{d y}{d x}\) + 4y = 0, which is the reqd. differential equation.

Question 3.
Solve the following differentia equation:
\(\frac{d y}{d x}\) + y = cos x – sin x (Outside Delhi 2019)
Solution:
The given differential equation is :
\(\frac{d y}{d x}\) + y = cos x – sin x dx Linear Equation
∴ I.F. = e^∫1dx = e^x
The solution is :
y.e^x = ∫ (cos x — sin x) e^x dx + C
⇒ y.e^x = e^x cos x + C
or y = cos x + C e^-x

Question 4.
Solve the following differential equation :
\(\frac{d x}{d y}\) + x = (tan y + sec²y). (Outside Delhi 2019 C)
Solution:
The given differential equation is :
\(\frac{d x}{d y}\) + x = (tany + sec²y).
Linear Equation
∵ I.F. = Jldy = ey
∴ The solution is :
x. ey = ∫ ey (tan y + sec² y)dy + c
⇒ x. ey = ey tan y + c
= x = tan y + c e-y, which is the reqd. solution.

Differential Equations Important Extra Questions Long Answer Type 1

Question 1.
Solve the differential equation
(x² – y²)dx + 2xydy = 0 (C.B.S.E. 2018)
Solution:

log x = -log (1 + v²) + log C
x(1 + v²) = C
x(1 + \(\frac{y^{2}}{x^{2}}\)) = C
x² + y² = C.

Question 2.
Find the particular solution of the differential equation (1 + x²)\(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^{2}}\), given that y = 0 when x = 1(C.B.S.E. 2018 C)
Solution:

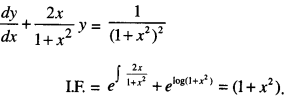
Solution is y( 1 + x²) = \(\int \frac{1}{1+x^{2}} d x\)
= tan^-1 x + C
When y = 0,x = 1,
then 0 = \(\frac{\pi}{4}\) + C
C = \(\frac{\pi}{4}\)
∴ y(1 + x²) = tan ^-1 x – \(\frac{\pi}{4}\)
i.e, y = \(\frac{\tan ^{-1} x}{1+x^{2}}-\frac{\pi}{4\left(1+x^{2}\right)}\)

Question 3.
Find the differential equation representing the family of curves y = ae^{bx + 5}, where ‘a’and ‘A’are arbitrary constants. {C.B.S.E. 2018)
Solution:
We have: y = ae^{bx + 5} + 5 …(1)
Diff. w.r.t. x, \(\frac{d y}{d x}\) = ae^{bx + 5}. (b)
\(\frac{d y}{d x}\) = dy ……(2) [Using (1)]]
Again diff. w.r.t x.,
\(\frac{d^{2} y}{d x^{2}}=b \frac{d y}{d x}\) ………(3)

Dividing (3) by (2),

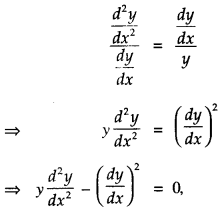
which is the required differential equation.

Question 4.
Find the particular solution of the differential equation x dx – ye^y \(\sqrt{1+x^{2}}\) dy = 0, given that y = 1 when x = 0. (C.B.S.E. 2019 C)
Solution:
The given differential equation is:

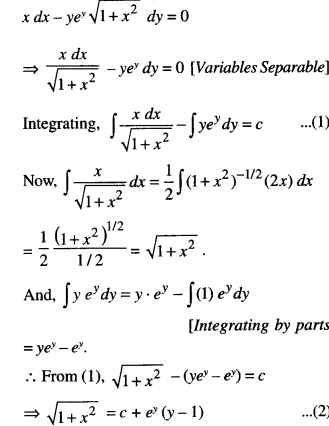
When x = 0,y = 1, ∴ 1 = c + c(0) ⇒ c = 1.
Putting in (2), \(\sqrt{1+x^{2}}\) = 1 + e^y(y -1),
which is the reqd. particular solution.

Question 5.
Obtain the differential equation of the family of circles, which touch the x-axis at the origin.   (N.C.E.R.T.; C.B.S.E. Sample Paper 2018)
Solution:
Let (0, α) be the centre of any member of the family of circles.

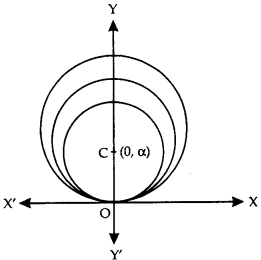
Then the equation of the family of circles is : x² + (y-α)² = α²
⇒ x² + y² – 2αy = 0 …(1)
Diff. w.r.t. x, 2x + 2y \(\frac{d y}{d x}\) 2α \(\frac{d y}{d x}\) = 0

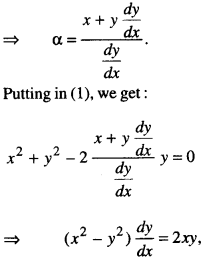
which is the required differential equation.

Question 6.
Obtain the differential equation representing the family of parabolas having vertex at the origin and axis along the positive direction of x-axis. (N.C.E.R.T.)
Solution:
Let S (a, 0) be the focus of any member of the family of parabolas.
Then the equation of the family of curves is y² = 4 ax …………. (1)
Diff. w.r.t. x, 2y\(\frac{d y}{d x}\) = 4a ……………. (2)
Using (2) in (1), we get:
y² = (2y\(\frac{d y}{d x}\))x

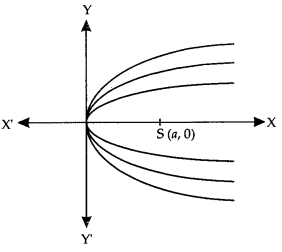
y² – 2xy\(\frac{d y}{d x}\) = 0
which is the required differential equation.

Question 7.
Find the general solution of the differential equation:
(tan²x + 2 tanx + 5) \(\frac{d y}{d x}\) = 2 (1 + tanx) sec² x
Solution:
We have : (tan² x + 2 tan x + 5)\(\frac{d y}{d x}\)
= 2 (1 + tanx) sec²x
Integrating

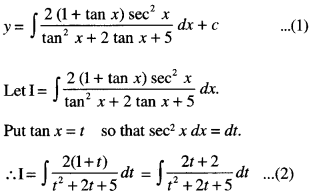
Put t² + 2t + 5 = z
so that (2t+ 2) dt = dz.
∴ From (2),
1 = \(\int \frac{d z}{z}\) = log| z | = log |t² + 2t + 5|
= log |tan² x| + 2 tan x + 5|
From (1), y = log |tan² x| + 2 tan x + 5| + c,
which is the required general solution.

Question 8.
Solve the differential equation:
(x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1 ; y(0) = 0. (C.B.S.E. 2019)
Solution:
The given equation can be written as :
\(\frac{d y}{2 e^{-y}-1}=\frac{d x}{x+1}\)
| Variables Separable

Integrating, \(\int \frac{e^{y} d y}{2-e^{y}}=\int \frac{d x}{x+1}\)
⇒ – log |2 – e^y| + log |C| = log |x + 1|
⇒ (2 – e^y) (x + 1) = C.
When x = 0, y = 0, then C = 1.
Hence, the solution is (2 – e^y) (x + 1) = 1.

Question 9.
Solve: (a) (i) \(\frac{d y}{d x}\) = 1 + x + y + xy
(ii) xyy’ = 1 + x + y + xy. (N.C.E.R.T.)
(b) Find the particular solution of the differential dy
equation \(\frac{d y}{d x}\) = 1 + x + y + xy, given that y = 0 when x = 1. (A.I.C.B.S.E. 2014)
Solution:
(a), (i) The given equation is :
\(\frac{d y}{d x}\) = 1 + x + y + xy
\(\frac{d y}{d x}\) = (1 +x) (1 +y)
\(\frac{d}{1+y}\) = (1 + x)dx.
|Variables Separable

Integrating,
\(\int \frac{d y}{1+y}\) = ∫(1 + x)dx + c
⇒ log |1 + y | = x + \(\frac { 1 }{ 2 }\) x² + c,
which is the required solution.

(ii) The given equation is xyy’ = 1 + x + y + xy
⇒ xy\(\int \frac{d y}{1+y}\) = (1 + x)(1 + y)

= y – log|1 + y| = log|x|+ x + c
= x + log |x (1 + y)|+ c,
which is the required solution.

(b) From part (a) (i),
Iog|1+y| = x + \(\frac { 1 }{ 2 }\)x² + c …(1)
When x = 1, y = 0, then:
log |1+0|= 1 + \(\frac { 1 }{ 2 }\)(1)² + c
log 1 = 1 + \(\frac { 1 }{ 2 }\) + c
0 = \(\frac { 3 }{ 2 }\) + c
c = \(-\frac { 3 }{ 2 }\)
Putting in (1), log |1 + y| = x + \(\frac { 1 }{ 2 }\)x² – \(\frac { 3 }{ 2 }\)
which is the required particular solution.

Question 10.
Solve the differential equation:
\(\frac{d y}{d x}\) = 1 + x² + y² + x²y²
given thaty = 1 when x = 0. (Outside Delhi 2019)
Solution:
The given equation is \(\frac{d y}{d x}\) = 1 + x² + y² + x²y²
⇒ \(\frac{d y}{d x}\) = (1+x²)(1 +y²)
⇒ \(\frac{d y}{1+y^{2}}\) (x² + 1) dx
|Variables Separable

Integrating, ∫\(\frac{d y}{1+y^{2}}\) = ∫(x² + 1) dx + C
tan^-1y = \(\frac{x^{3}}{3}\) + x + C ………. (1)
Where x = 0,y = 1,
∴ tan^-1 (1) = C
C = \(\frac{\pi}{4}\)
Putting in (1),
tan^-1 y = \(\frac{x^{3}}{3}+x+\frac{\pi}{4}\)
which is the reqd. particular solution.

Question 11.
Find the particular solution of the differential equation: e^x tan y dx + (2 – e^x) sec² y dy = 0, given thaty = \(\frac{\pi}{4}\) where x = 0.
Solution:
The given differential equation is:

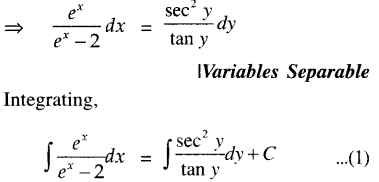
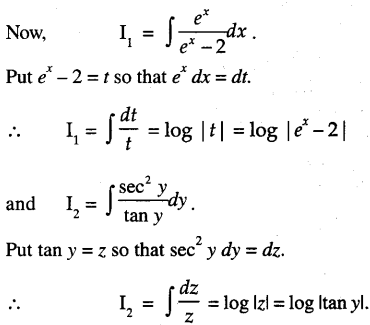
∴ From (1),
log C + log |e^x – 2| = log |tan y|
⇒ tany = C(e^x – 2) …(2)
When x = 0, y = y = \(\frac{\pi}{4}\)
∴ 1 = C(1 – 2)
C = -1
Putting in (2),
tan y = 2 – e^x
which is the required particular solution.

Question 12.
Find the particular solution of the following differential equation:
cosy dx + (1 + 2e^-x) siny dy = 0; y(0) = \(\frac{\pi}{4}\) .
(CBSE Sample Paper 2018 – 19)
Solution:
The given differential equation is:
cos y dx + (1 + 2e^-x) sin ydy = 0

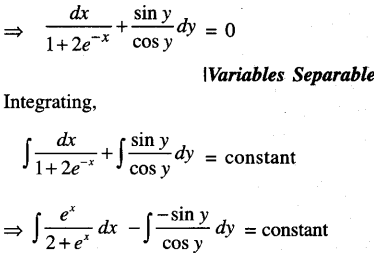
log |e^x| – log |cos y| = log|C|
e^x + 2 = C cos y ….. (1)

Substituting, x = 0, y = \(=\frac{\pi}{4}\) in(1),we get:
1 + 2 = C cos \(=\frac{\pi}{4}\)
C = \(\frac{3}{1 / \sqrt{2}}\)
C = 3√2
Putting in (1),
e^x + 2 = 3√2 cos y
which is the required particular solution.

Question 13.
Find the particular solution of the following differential equation:
(x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1 ; y = 0 when x = 0. (C.B.S.E. 2012)
Solution:
The given equation is (x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1

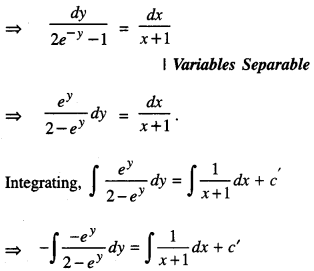
-log|2 – e^y| = log|x + 1| + log|c|,
where c’ = log |c|
⇒ log \(\left|\frac{1}{2-e^{y}}\right|\) = log |c(x + 1)|
⇒ \(\frac{1}{2-e^{y}}\) = c(x + 1)
When x = 0, y = 0;
\(\frac{1}{2-e^{0}}\) = c(0 + 1)
⇒ c = \(\frac{1}{2-1}=\frac{1}{1}\) = 1

Putting (1)
\(\frac{1}{2-e^{y}}\) = 1.(x + 1)
⇒ (x + 1)(2 – e^y) = 1
which is the required particular solution.

Question 14.
Solve the differential equation:
(1 – y²) (1 + log x)dx + 2xy dy = 0, given that when x = 1 ,y = 0.
(C.B.S.E. 2016)
Solution:
The given equation is :
(1 – y²) (1 + log x)dx + 2xy dy = 0

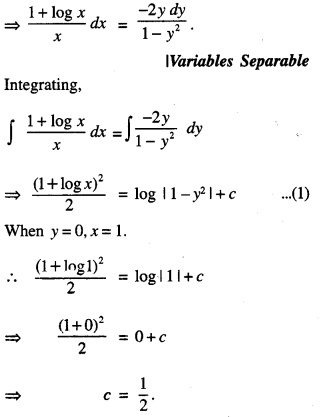
Putting in (1),
\(\frac{(1+\log x)^{2}}{2}\) = log|1 – y²| + 1/2
(1 + log x)² = 2 log|1 – y²| + 1
which is the required solution.

Question 15.
Solve the differential equation:
x cos x (\(\frac { y }{ x }\)) \(\frac{d y}{d x}\) = y cos(\(\frac { y }{ x }\)) = x (C.B.S.E. 2019 C)
Solution:
The given equation is:

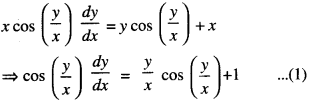
Put \(\frac { y }{ x }\) = v i.e, y = vx so that \(\frac { dy }{ dx }\) = v + x \(\frac { dv }{ dx }\)
∴ (1) becomes:
cos v (v + x\(\frac { dv }{ dx }\)) = vcosv + 1
= v + x \(\frac { dv }{ dx }\) = v + \(\frac { 1 }{ cos v }\)
x \(\frac { dv }{ dx }\) = \(\frac { 1 }{ cos v }\)
cos v dv = \(\frac { dx }{ x }\)
[Variables Seperable]

Integrating, ∫ cos v dv = ∫ \(\frac{d x}{ x}\) + c
sin = log|x| + c
sin \(\frac{y}{ x}\) = log|x| + c,
which is the reqd. solution.

Question 16.
Find the general solution of the differential equation: \(\frac{d x}{d y}=\frac{y \tan y-x \tan y-x y}{y \tan y}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
The given differential equation is :

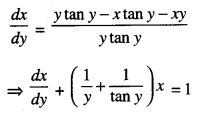
|Linear Equation
Comparing with \(\frac{d x}{d y}\) + Py = Q, we have :
‘P’ = \(\frac{1}{y}+\frac{1}{\tan y}\) and ‘Q’ = 1

∴ I.F = \(e^{\int\left(\frac{1}{y}+\frac{1}{\tan y}\right) d y}=e^{\log y+\log \sin y}\)
e^log(ysiny) = ysiny.
∴ The solution is
x x I.F. = ∫ (Q x I.F.)dy + C
⇒ x(y sin y) = ∫(1 x y sin y)dy + C
⇒ xy sin y = ∫ y sin y dy + C
⇒ xy sin y = y (- cos y) – ∫(1) -cos y)dy + C

(Integrating by Parts)
⇒ xy sin y = – y cos y + ∫ cos ydy + C
⇒ xy sin y = – y cos y + sin y + C
⇒ x = \(\frac{\sin y-y \cos y+C}{y \sin y}\)
which is the required general solution.

Question 17.
Solve the differential equation :
xdy – ydx = \(\sqrt{x^{2}+y^{2}}\) dx , given that y = 0 when x = 1. (C.B.S.E. 2019)
Solution:
The given equation can be written as :


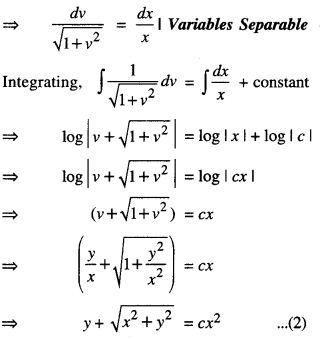
where x = 1, y = 0
∴ 0 + \(\sqrt{1+0} \) = c(1)
⇒ c = 1
Putting in (2), y + \(\sqrt{x^{2}+y^{2}}\) = x²,
which is the reqd. solutions.

Question 18.
Solve the following differential equation:
\(x y \log \left(\frac{y}{x}\right) d x+\left(y^{2}-x^{2} \log \left(\frac{y}{x}\right)\right) d y=0\) (C.B.S.E. 2010 C)
Solution:
The given equation can be written as:

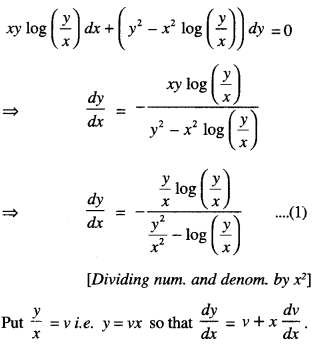
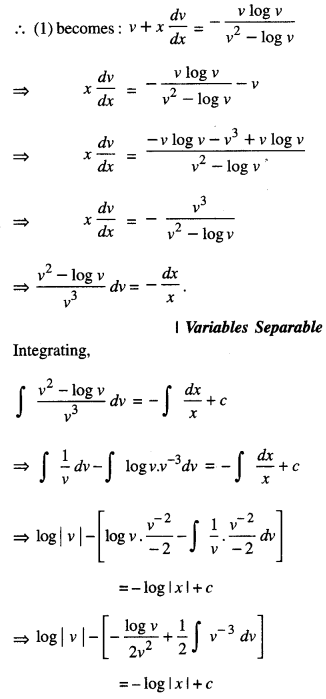
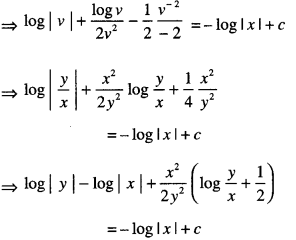
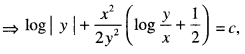
Question 19.
Solve the differential equation:
xdy-y dx= \(\sqrt{x^{2}+y^{2}}\) dx.
(iC.B.S.E. Sample Paper 2019)
Solution:
The given differential equation is:

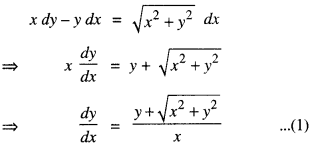
Put y = vx, so that \(\frac{d y}{d x}\) = dv + x \(\frac{d v}{d x}\)
(1) becomes:

⇒ y+ \(\sqrt{x^{2}+y^{2}}\) = cx²,
which is the reqd. solution.

Question 20.
Prove that x² – y² = c(x² + y²)² is the general solution of the differential equation: (x³ – 3xy²)dx = (y³ – 3x²y)dy, where c is a parameter. (C.B.S.E. 2017)
Solution:
We have :(x³ – 3xy²) dx = (y³ – 3x²y)dy

∴ v³ – 3v = A(1 + v)(1 + v²) + B(1 – v) (1 + v²) + (Cv + D) (1 – v²).
Putting v= 1,
1-3 = A(2) (2)
⇒ A = -1/2

Putiing v = -1, -1 + 3 = B(2)(1 + 1)
⇒ B = 1/2

Putting v = 0
⇒ 0 = A(1)(1) + B(1)(1) + D(1)
⇒ 0 = \(-\frac{1}{2}+\frac{1}{2}\) + D
D = 0
Comparing coeff. of v³, 1 = A – B – C
⇒ C = A – B – 1 = \(-\frac{1}{2}-\frac{1}{2}\) – 1 = -2
∴ From (2),

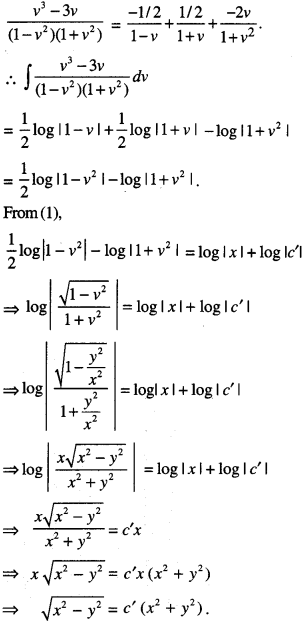
Squaring , x² – y² = c’²(x²+ y²)²
⇒ x² – y² = c’² (x² + y² )²
where c’² = c,
which is the required solution.

Question 21.
Show that the differential equation:
2ye^x/y dx + (y – 2x e^x/y) dy = 0 is homogeneous and find the particular solution, given that x = 0 when y = 1. (C.B.S.E. 2013)
Solution:
(i) The given equation is :
2ye^x/y dx + (y – 2x e^x/y) dy = 0

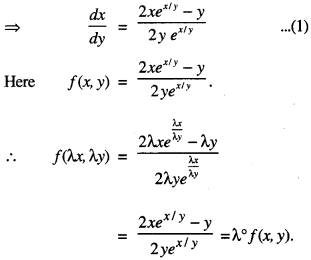
Thus f(x, y) is homogeneous function of degree zero.

⇒ 2e^v = – log |y| + c
⇒ e^x/y = -log|y| + c …………….(2)

Now x = 0 when y = 1,
∴ 2(1) = -log |1| + c
⇒ 2 = – log 1 + c
⇒ 2 = —0 + c
⇒ c = 2.

Putting in (2),
2e^x/y = – log |y|+ 2,
which is the required solution.

Question 22.
Solve the differential equation:
(1 + x²)\(\frac{d y}{d x}\) + 2xy – 4x² =0, subject to the initial condition y (0) = 0. (C.B.S.E. 2019)
Solution:
The given equation can be written as :

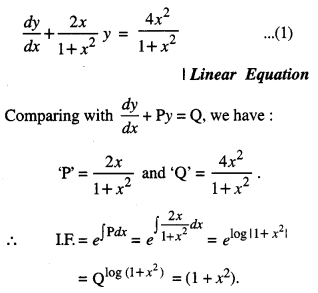
Multiplying (1) by (1 + x²), we get:
(1 + x²)\(\frac{d y}{d x}\) + 2xy = 4x² dx
⇒ \(\frac{d}{d x}\) y.(1 + x²) = 4x²

Integrating, y.(1 + x²) = ∫ 4x² dx = \(\frac{4 x^{3}}{3}\) + C
⇒ y(1 + x²) = \(\frac{4}{3}\) x² + C …(2)
When x = 0, y = 0,
∴ C = 0 + C
⇒ C = 0.
ry 4 T
Putting in (2), y(1 + x²) = \(\frac{4}{3}\) x³ , which is the required solution.

Question 23.
Solve the differential equation :
\(\frac{d y}{d x}-\frac{2 x}{1+x^{2}} y\) = x² + 2 (C.B.S.E. 2019)
Solution:
The given equation is :

Hence, y = (1 + x²) (x + tan^-1 x + C).

Question 24.
Find the general solution of the following differential equation:
(1 + y²) + (x – e^tan-1y)\(\frac{d y}{d x}\) (C.B.S.E. 2016)
Solution:
The given equation is:


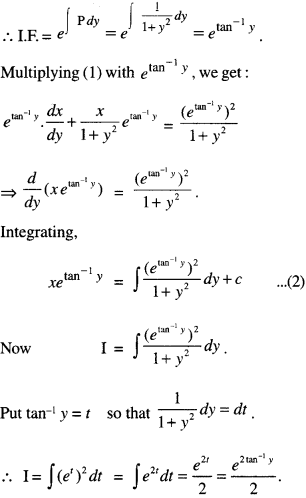
Putting xee^tan-1y = \(\frac{1}{2}\)e^2tan-1y + c
x = \(\frac{1}{2}\)e^tan-1y + c
which is the required solution.

Question 25.
(i) Solve the differential equation:
(tan^-1 y – x)dy = (1 + y²) dx. (N.C.E.R.T.; C.B.S.E. 2015)
(ii) Find the particular solution when x = 0, y = 0. (A.I.C.B.S.E. 2013)
Solution:
(i) The given equation can be written as :
\(\frac{d x}{d y}+\frac{x}{1+y^{2}}=\frac{\tan ^{-1} y}{1+y^{2}}\) …… (1)
Comparing with \(\frac{d x}{d y}\)+ Px = Q , we have:


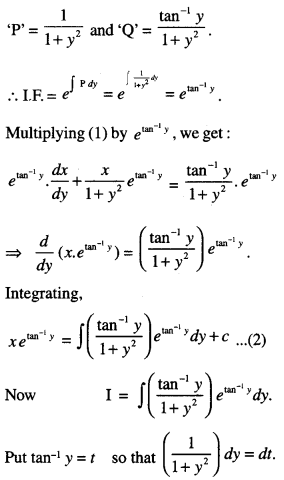
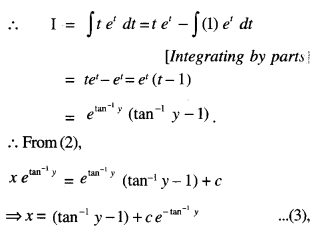
which is the required solution.

(ii) When
x – 0, y = 0.
0 = (tan^-10 – 1) + ce-tan^-10,
⇒ 0 – (0 – 1) + ce^-0
⇒ 0 = – 1 + c
⇒ c = 1.
Putting in (3),
x = (tan^-1 y – 1) + e^-tan-1y,
which is the required particular solution.