The Solid State Class 12 Notes Chemistry Chapter 1

By going through these CBSE Class 12 Chemistry Notes Chapter 1 The Solid State, students can recall all the concepts quickly.

The Solid State Notes Class 12 Chemistry Chapter 1

A solid is defined as that form of matter which possesses rigidity and hence possesses a definite shape and a definite volume.

The following are the characteristic properties of the solid-state:

1. They have definite mass, volume, and shape.
2. Intermolecular distances are short.
3. Intermolecular forces are strong.
4. Their constituent particles (atoms, molecules, or ions) have fixed positions and can only oscillate about their mean positions.
5. They are incompressible and rigid.

Solids can be classified into two classes:
1. Crystalline Solids: The substances whose constituents are arranged in a definite orderly arrangement are called crystalline solids. For example, NaCl, S, diamond, sugar, etc. The crystalline substances have sharp melting points and have physical properties different in different directions, i.e., crystalline substances are ANISOTROPIC. They have long-range and short-range orders.

2. Amorphous Substances: The substances whose constituents are not arranged in an orderly arrangement are called amorphous substances. For example, glass, rubber, fused silica, plastics, etc. They do not have sharp melting points and their physical properties are the same in all directions, i.e., there are ISOTROPIC. They have short-range orders.

The difference in their characteristics are:

Crystalline Solids	Amorphous Solids
1. Arrangement of constituents: Crystalline solids have an orderly arrangement of constituents. Thus they have definite regular geometry.	1. Amorphous substances do not possess an orderly arrangement.
2. Interfacial angles: Crystals are always bounded by planes so that a definite angle between two planes exists.	2. Amorphous substances are not bound by plane faces; so do not possess interfacial angles.
3. Anisotropy: Crystalline solids exhibit anisotropy i.e. their physical properties are different in different directions.	3. Amorphous substances like liquids have the properties same in all directions. Therefore, they are called to be isotropic.
4. Melting points: Melting points in crystalline solids are sharp and distinct.	4. These do not have sharp melting points e.g., glass on heating softens and starts flowing
5. Heat of fusion: These have definite heat of fusion.	5. Amorphous solids do not have definite heat of fusion.
6. Nature: They are true solids.	6. Pseudo solids or supercooled liquids.
7. Order in the arrangement of constituent particles: Long-range order	7. Only short-range order.

Classification of Crystalline Solids:
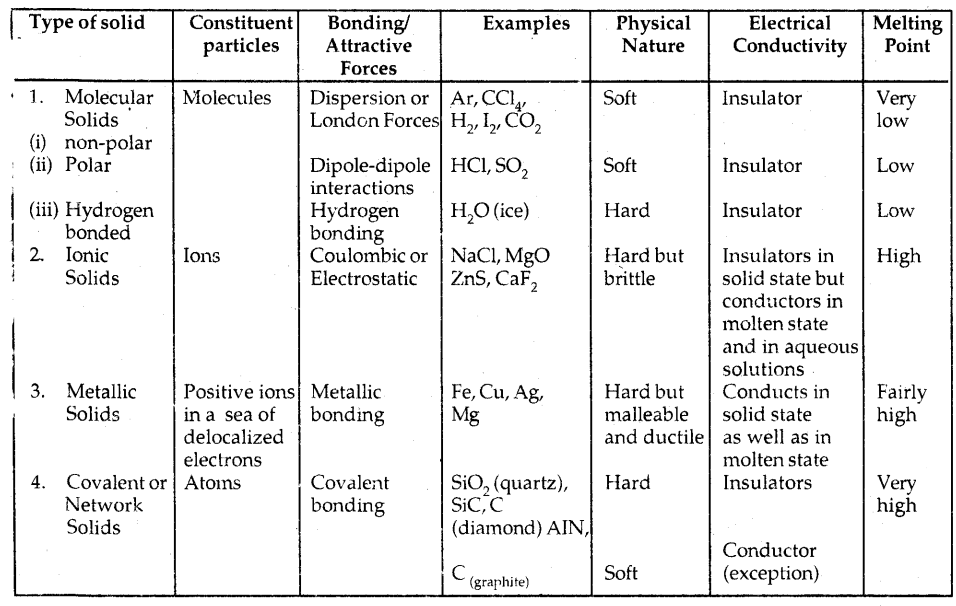
1. Molecular solids: These solids have molecules as constituent particles.

They are further subdivided into.
→ Non-polar molecular solids: They comprise either atoms, e.g., argon and helium, or the molecules formed by non-polar covalent bonds, for example, -H₂, Cl₂, and I₂. They are held by weak dispersion forces or London forces. These solids are soft and non-conductors of electricity. They have low melting points and are usually liquids or gases at room temperature and pressure.

→ Polar molecular solids: The molecules of substances like HCl and SO₂ etc. are formed by polar covalent bonds. The molecules in such solids are held together by relatively stronger dipole-dipole interactions. They are soft solids and non-conductors of electricity. Their melting points are higher than non-polar molecular solids. They are mostly liquids and gases at room temperature and pressure. Solid SO₂ and solid NH₃, are some of the examples of such solids.

→ Hydrogen bonded molecular solids: The molecules of such solids contain polar-covalent bonds between H and F, O or N atoms. Strong hydrogen bonds bind the molecules of such solids like H₂O (ice). They are non-conductors of electricity. Generally, they are volatile liquids or soft solids under room temperature and pressure.

2. Ionic Solids: They comprise ions. They are formed by three-dimensional arrangements of cations and anions bound by strong Coulombic forces. These solids are hard and brittle. They have high melting and boiling points. Since ions are not free to move they are electrical insulators in the solid-state. These ions become mobile in molten or aqueous states. Hence they conduct electricity in their molten or aqueous state.

3. Metallic Solids: Metals are an orderly collection of positive ions (kernels) surrounded by and held together by a sea of mobile or free electrons. These mobile electrons are responsible for the high electrical and thermal conductivity of metals. They are also responsible for the color and luster of metals. Metals are highly malleable and ductile.

4. Covalent or Network Solids: A wide variety of crystalline solids of non-metals results from the formation of covalent bonds between adjacent atoms throughout the crystal. They are giant-sized molecules. Covalent bonds are strong and directional in nature. Such solids are hard and brittle. They have extremely high melting points and even decompose before melting. They are insulators and do not conduct electricity. Diamond and silicon carbide (SiC) are typical examples of such solids. Graphite is soft and conductor of electricity.

The different properties of the four types of solids are listed in the table below:
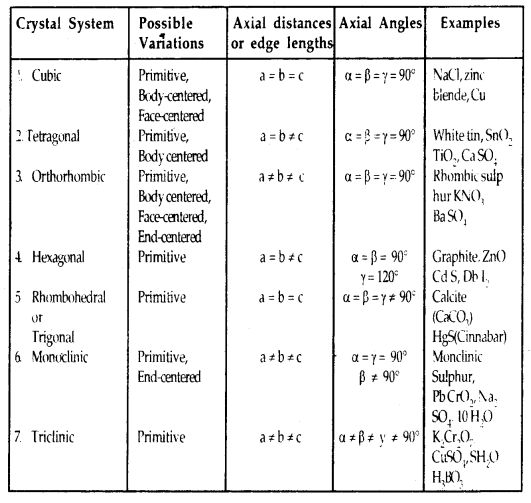
Crystal Lattices and Unit Cells: A regular three-dimensional arrangement of points in space is called a Crystal Lattice.

There are only 14 possible three-dimensional lattices. These are called Bra Vais Lattices.

Characteristics of a crystal lattice

1. Each point in a lattice is called a lattice point or lattice site.
2. Each point in a crystal lattice represents one constituent particle which may be an atom, molecule, or ion.
3. Lattice points are joined by straight lines to bring out the geometry of the lattices.

Unit Cell is the smallest portion of a crystal lattice which, when repeated in different directions venerates the entire lattice.

Table: Different Types Of Solids:

A unit cell is characterized by

1. Its dimensions along the three edges a, b and c. These edges may or may not be mutually perpendicular.
2. Angles between the edges, α (between b and c), β (between a and c), and γ (between a and b). Thus a unit cell is characterized by 6 parameters: a, b, c, α, β and γ.

These parameters of a typical unit cell are shown in the figure below:

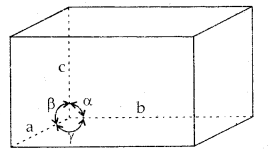
Illustration of parameters of a unit cell

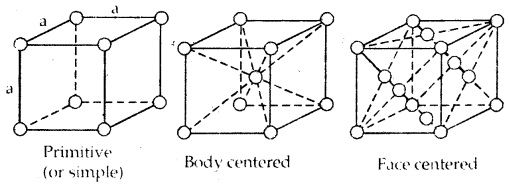
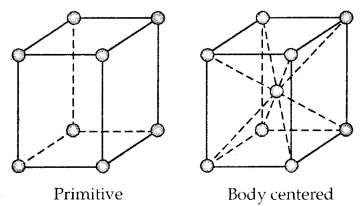
Primitive And Centered Unit Cells:
Unit cells can be broadly divided into two categories, primitive and centered unit cells.
1. Primitive Unit Cells: When constituent particles are present only on the corner positions of a unit cell, it is called a primitive unit cell.

2. Centered Unit Cells: When a unit cell contains one or more constituent particles present at positions other than corners in addition to those at comers, it is called a centered unit cell.

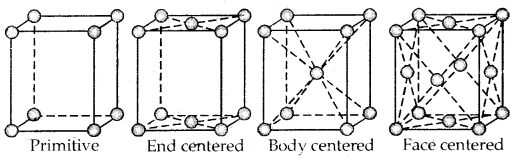
Centered unit cells are of three types:
(a) Body-Centered Unit Cells: Such a unit cell contains one constituent particle (atom, molecules, or ion) at its body center beside the ones that are at its corners.

(b) Face-Centered Unit Cells: Such a unit cell contains one constituent particle present at the center of its face, besides the ones that are at its corners

(c) End-Centered Unit Cells: In such a unit cell, one constituent particle is present at the center of any two opposite faces besides the ones present at its corners.

In all, there are seven types of primitive unit cells.

Table 1.2: Seven primitive unit cells and their possible variations as centered units

Unit Cells Of 14 Types Of Bra Vais Lattices:

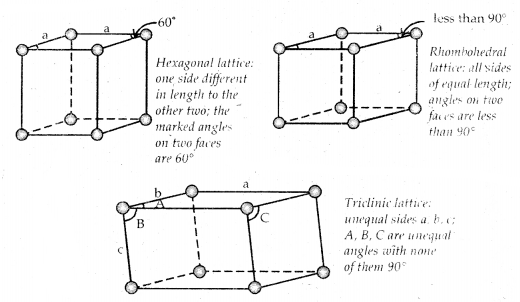
→ The three cubic lattices: all sides of name length angles between faces all 90°

→ The two tetragonal: one side different in length to the other two angles between faces all 90°

→ The four orthorhombic lattices: unequal sides; angles between faces all 90°

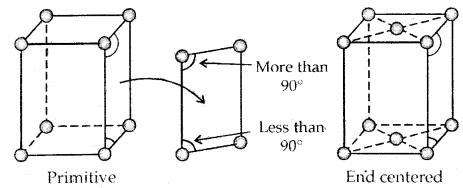
→ The two monoclinic lattice: unequal sides; two faces have angles different to 90°

Number Of Atoms In A Unit Cell:
1. Primitive Cubic Unit Cell: Primitive cubic unit cell has atoms only at its corner. Each atom at a comer is shared between eight adjacent unit cells as shown in the figure below, four-unit cells in the same layer and four-unit cells of the upper (or lower) layer. Therefore only l /8th of an atom (molecule or ion) actually belongs to a particular unit cell.

In all, since each cubic unit cell has 8 atoms on its corners, the total number of atoms in one unit cell is 8 × \(\frac{1}{8}\) = 1 atom.

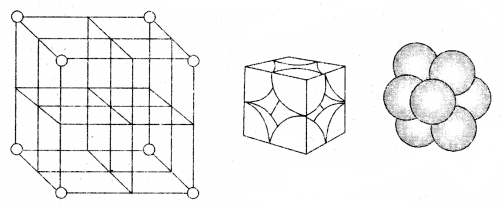
In a simple cubic unit cell, each corner atom is shared between 8 unit cells.

2. Body-Centered Cubic Unit Cell: A body-centered cubic (bcc) unit cell has an atom at each of its corners and also one atom at its body center. Fig. depicts such a structure.

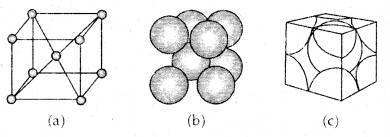
(a) open structure
(b) space-filling model and
(c) the unit cell with portions of atoms actually belonging to it.

It can be seen that the atom at the body center wholly belongs to the unit cell in which it is present. Thus in a body-centered cubic (bcc) unit cell:

1. 8 corners × \(\frac{1}{8}\) per corner atom = 8 × \(\frac{1}{8}\) = 1 atom
2. 1 body centre atom = 1 × 1 = 1 atom
   ∴ Total number of atoms per unit cell = 2 atoms

3. Face Centered Cubic unit cell: A face-centered cubic (fee) unit cell contains atoms at all the comers and at the center of all the faces of the cube. Each atom located at the face-center is shared between two adjacent unit cells and only \(\frac{1}{2}\) of each atom belong. to a unit cell. The figure below depicts such a structure.

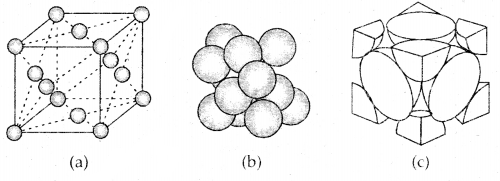
(a) open structure
(b) space-filling model and
(c) the unit cell with portions of atoms actually belonging to it.

Thus in a face-centered cubic face unit cell.

1. 8 corners × \(\frac{1}{8}\) per corner atom = 8 × \(\frac{1}{8}\) = 1 atom
2. 6 face-centered atoms × \(\frac{1}{2}\) atom per unit cell = 6 × \(\frac{1}{2}\) = 3 atoms
   ∴ Total number of atoms per unit cell = 4 atoms

Close Packing Of Particles:
There are two common types of close packing of particles in a crystalline substance.
→ Hexagonal Close-Packing: This type of packing is referred to as the ABABA arrangement.

→ Cubic Close-Packing: This type of packing is referred to as

ABC ABC arrangement. In both types of packing, 74% of the available space is occupied by spheres.

Interstitial Sites: Two important interstitial sites are:
1. Tetrahedral Sites: When a sphere in the second layer is placed above three spheres that are touching each other, a tetrahedral site is formed. There are two tetrahedral sites for each sphere.

2. Octahedral Site: This type of site is formed at the center of six spheres and is produced by two sets of equilateral triangles which point in opposite directions. There is one octahedral site for each sphere.

Coordination Number And Radius Ratio: The ratio of the radius of the cation to the radius of an anion is called the Radius Ratio.
Radius ratio =\(\frac{\gamma_{+}}{\gamma}\); where γ+: radius of cation
γ-: radius of anion

→ It is very important to determine the structure of IONIC SOLIDS like Na⁺ Cl^–, Cs₄Cl^–, etc.

→ The number of spheres that are touching a given sphere is called the Coordination Number.

→ It may be remembered that coordination numbers of 4,6,8 and 12 are very common in various types of crystals.

Radius’Ratios in Crystals

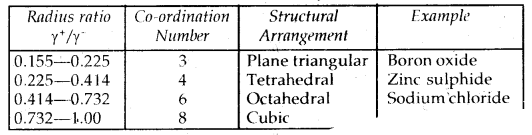
It may be mentioned here that, although a large number of ionic substances obey this rule, there are many exceptions to this rule.

Structure of Sodium Chloride (NaCl) Rock-Salt Structure: It has a cubic closed packed structure i.e. face-centered cubic.

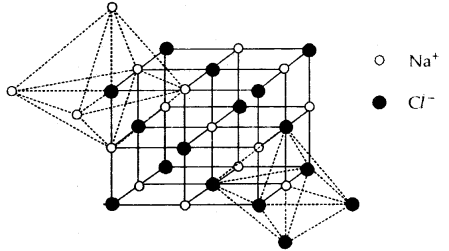
1. The Na⁺ ions (represented by o) occupy the octahedral holes in the ccp lattice of Cl^– ions (represented by •)
2. Each Na⁺ is surrounded by 6 Cl^– and vice-versa.
3. Na⁺ and Cl^– have 6: 6 fold coordination.

Table 1.3: Some Cubic Ionic Solids

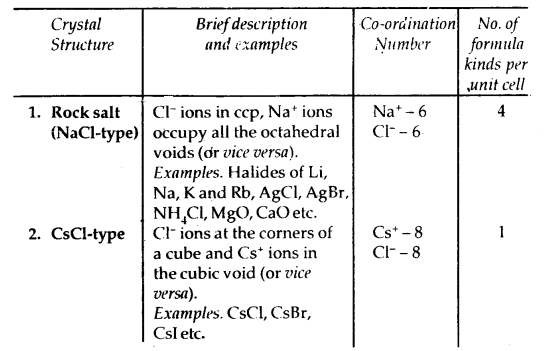
Caesium Chloride (CsCl) Structure

1. In this structure, the Cl^– ions are at the comers of a cube whereas Cs₄ ion is at the center of the cube or vice versa as shown.
2. This structure has 8: 8 coordination, i.e., each Cs⁺ ion is touching eight Cl^– ions, and each Cl^– ion is touching eight Cs⁺ ions.
3. For exact fitting of Cs ions in, the cubic voids the ratio \(\frac{\mathrm{r}_{\mathrm{Cs}^{+}}}{\mathrm{r}_{\mathrm{Cl}^{-}}}\) should he equal to 0.732, however, actually the ratio is slightly larger (0.932). Therefore, packing of C1 ions slightly opens up to accommodate Cs4 ions.
4. The unit cell of caesium chloride has one Cs+ ion and one Cl~ ion as calculated below:
   .No. of Cl- ions = 8 (At corners) × \(\frac{1}{8}\) = 1
   No. of Cs+ ions = 1 (At the body centre) × 1 = 1
   Thus, no. of CsCl units per unit cell is 1.

Examples of the compounds having this type of structure are CsBr, Csl, TICl, and TIBr.

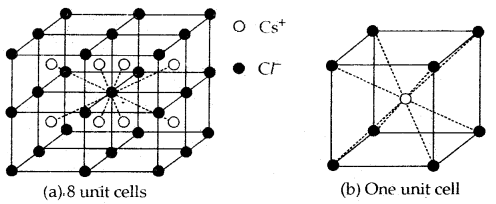
Cesium chloride structure

It may be mentioned here that temperature and pressure also affect the structure of an ionic solid. For example, at ordinary temperatures and pressures, chlorides, bromides, and iodides of lithium, sodium, potassium, and rubidium possess the NaCl structure with 6: 6 coordination.

It is observed that on the application of high pressure they transform to the CsCl structure with 8: 8 coordination. Thus, high pressure increases the coordination number. Ort the other hand, CsCl on heating transforms to the NaCl structure at 760 K. Thus, at higher temperature coordination number decreases.

Point Defects in Crystals: Ideal crystals with the perfect arrangement of constituents are found only at 0°K. Above this temperature, all crystalline solids have some defects in the arrangement of their unit. An ideal crystal of A⁺ B^– type may be represented as shown in Fig.

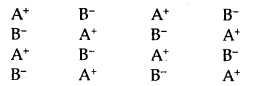
Ideal Crystal A⁺ B^–

Defects in the crystals may give rise to
(A) Stoichiometric and
(B) Nonstoichiometric structures

(A) Stoichiometric structures: The compound A⁺ B^– is stoichiometric if it contains an equal number of ions A⁺ and B^– as suggested by the chemical formula of the compound. There are three types of defects in stoichiometric structures:
1. Schottky Defect. This defect consists of vacancies at cation sites and an equal number of vacancies at anion sites. It is predominant in compounds with high coordination numbers and where the ions are of similar size. ‘

2. Frenkel Defect. This defect consists of vacancies at cation sites in which the cation moves to another position in between two layers called interstitial sites. This defect is most predominant in compounds which have low coordination number and ions of different sizes.

3. Interstitial Defect: When some constituent particles occupy an interstitial site the crystal is said to have an interstitial defect. This defect increases the density of the substance.

(B) Nonstoichiometric Compounds: The compounds in which the ratio of the number of atoms of A⁺ to the number of atoms of B^– does not correspond to a simple whole number as suggested by the formula, are called nonstoichiometric compounds.

The nonstoichiometric defects are of two types:
1. Metal excess defects. In these defects, positive ions are in excess and arise due to.
(a) Anion vacancies: Vacancies at anion sites and their electrons remain trapped.

(b) Cation occupying Interstitial sites: Excess cations are present in interstitial sites and an equal number of electrons trapped.

2. Metal deficient defects. This arises due to
(a) Cation vacancies: Vacancies at cation sites and the extra negative charge is balanced by extra charge (higher oxidation state) of an equal number of some cations.

(b) Anion occupying Interstitial sites: Excess anions are present in interstitial sites and the corresponding increase in negative charge is balanced by oxidation of an equal number of cations to higher oxidation states.

1. Anion vacancy and electron remain trapped.
2. Cation occupying the interstitial site and electron trapped

2. (i) Cation vacancy and one A⁺ changes to A²⁺ . 2. (ii) Anion occupying the intertidal site and one A⁺ changes to A²⁺

Non-Stoichiometric Structures:
The examples of non-stoichiometric defects are in the crystals of FeO where the composition is Fe_0.93O to Fe_0.96O. This behavior is mostly found in Transition metals compounds. Electrons trapped in anionic vacancies are referred to as F-CENTRES [from the farbe-the German word for color]

It may be mentioned here that metal excess compounds and metal deficient compounds both act as semiconductors. Metal excess compounds conduct electricity through normal electron conduction mechanisms and are therefore n-type semiconductors. Metal deficient compounds conduct electricity through a positive hole conduction mechanism and are therefore p-type semiconductors.

Point Defects due to the Presence of Foreign Atoms:
So far we have discussed point defects where there are no foreign atoms. Foreign atoms can occupy interstitial or substitutional sites in a crystal. Solid solutions of group 13 or group 15 impurities with group 14 elements such as silicon or germanium are of great interest in the electronic industry as they are used to make transistors.

The group 13 elements such as AI and Ga and the group 15 elements such as P and As form substitutional solid solutions with Si and Ge. The group 15 elements have five valence electrons. After forming the four covalent bonds with the group 14 elements, one excess electron is left on them. The excess electrons give rise to electronic conduction (n-type conduction).

The group 13 elements have only three valence electrons. They combine with group 14 elements resulting in the formation of an electron-deficient bond or a hole. These holes give rise to positive hole conduction (p-type conduction). Silicon and germanium doped with group 13 or group, 15 elements impurities act as semi-conductors and have fairly high electrical conductivity. This type of conduction is known as extrinsic / conduction.

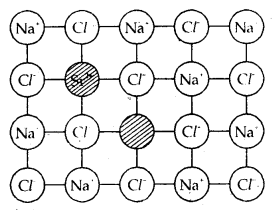
Introduction of a cation vacancy in NaCl by substitution of Na⁺ with Sr²⁺ ion.

Defects in the ionic solids may be introduced by adding impurity ions. If the impurity ions have a different valence state than that of the host ions, vacancies are created. For example, the addition of SrCl₂ to NaCl yields solid solutions where the divalent cation occupies Na⁺ sites and produces cation vacancies equal to the number of the divalent ions occupying substitutional sites. Similarly, AgCl crystals can be doped with CdCl₂ to produce impurity defects in a like-wise manner.

Electrical Properties: Solids exhibit an amazing range of electrical conductivities, extending over 27 orders of magnitude ranging from 10^-20 to 10⁷ ohm^-1 m^-1. Solids can be classified into three types on the basis of their conductivities.

1. Conductors: The solids with conductivities ranging between 10⁴ to 10⁷ ohm^-1 m^-1 are called conductors. Metals have conductivities in the order of 107 ohm’m1 and are good conductors.
2. Insulators: These are the solids with very low conductivities ranging between 10^-20 to 10^-10 ohm^-1 m^-1.
3. Semiconductors: These are the solids with conductivities in the intermediate range from 10^-6 to 10⁴ ohm^-1 m^-1.

Conduction of Electricity in Metals: A conductor may conduct electricity through the movement of electrons or ions. Meta (lie conductors belong to the former category and electrolytes to the latter.

Metals conduct electricity in solid as well as in the molten state. The conductivity of metals depends upon the number of valence electrons available per atom. The atomic orbitals of metal atoms from molecular orbitals are so close in energy to each other as to form a band. If this band is partially filled or it overlaps with a higher energy unoccupied conduction band, then electrons can flow easily under an applied electric field and the metal shows conductivity (Fig (a) below).

If the gap between the filled valence band and the next higher unoccupied band (conduction band) is large, electrons cannot jump to it and such a substance has very small conductivity and it behaves as an insulator. (Fig. (b) below)

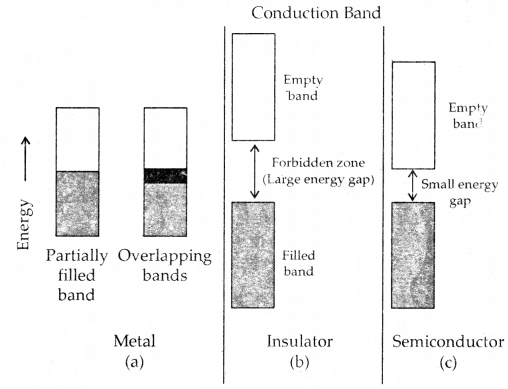
Distinction among (a) metals, (b) insulators and (c) semi-conductors.
In each case, an unshaded area represents a conduction band.

Conduction of Electricity in semiconductors: In the case of semiconductors, the tire gap between the valence band and conduction band is small (Fig. c). Therefore, some electrons may jump to the conduction band and show some conductivity. The electrical conductivity of semiconductors increases with rising temperature since more electrons can jump to the conduction band. Substances like silicon and germanium show this type of behavior and are called intrinsic semiconductors.

The conductivity of these intrinsic semiconductors is too low to be of practical use. Their conductivity is increased by adding an appropriate amount of suitable impurity. This process is called doping. Doping can be done with an impurity that is electron-rich or electron deficit as compared to the intrinsic semiconductor silicon or germanium. Such impurities introduce electronic defects in them.

Magnetic Properties: Solids can be classified into different types depending upon their behavior towards magnetic fields. The substances which are weakly repelled by a magnetic field are called diamagnetic substances. For example, TiO₂ and NaCl. Diamagnetic substances have all their electrons paired.

The substances which are weakly attracted by a magnetic field are called paramagnetic substances. These substances have permanent magnetic dipoles due to the presence of some species (atoms, ions, or molecules) with unpaired electrons. The paramagnetic substances lose their magnetism in the absence of a magnetic field. For example, TiO, VO, and CuO.

The substances which are strongly attracted by a magnetic field are called ferromagnetic substances. These substances show permanent magnetism even in the absence of a magnetic field. Some examples of ferromagnetic solids are iron, cobalt, nickel, and CEO.

Ferromagnetism arises due to the spontaneous alignment of magnetic moments of ions or atoms in the same direction. Alignment of magnetic moments in opposite direction in a compensatory manner and resulting in a zero magnetic moment (due to an equal number of parallel and antiparallel magnetic dipoles) give rise to antiferromagnetism.

For example, MnO, Mn₂O₃, and MnO₂ are antiferromagnetic. Alignment of magnetic moments in opposite directions resulting in a net magnetic moment (due to an unequal number of parallel and antiparallel magnetic dipoles) gives rise to ferrimagnetism.

For example, FeX > 4 is ferrimagnetic.

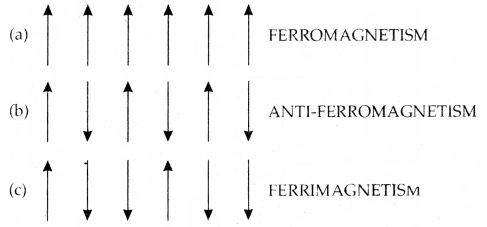
Alignment of magnetic dipoles in (a) ferromagnetic, (b) anti-ferromagnetic, and (c) ferrimagnetic substances.

Ferromagnetism and paramagnetic substances change into I paramagnetic substances at higher temperatures due to the randomization of spins. Fe₃O₄ which is ferrimagnetic at room temperature becomes paramagnetic at 850 K.