Electrochemistry Class 12 Notes Chemistry Chapter 3

By going through these CBSE Class 12 Chemistry Notes Chapter 3 Electrochemistry, students can recall all the concepts quickly.

Electrochemistry Notes Class 12 Chemistry Chapter 3

Electrochemical Cell: It is a device to convert the chemical energy of a spontaneous redox reaction into electrical energy. It is also called Galvanic Or Voltaic Cell. One such example of an electrochemical cell is Daniel Cell.

Daniel’s cell converts the chemical energy liberated during the redox reactions.
Zn (s) + Cu²⁺ (aq) → Zn²⁺ (aq) + Cu (s) into electrical energy and has an electrical potential [E.M.F. ] equal to 1.1 volt when concentration of both Zn²⁺ and Cu²⁺ ions is unity (1 mol dm^-3)

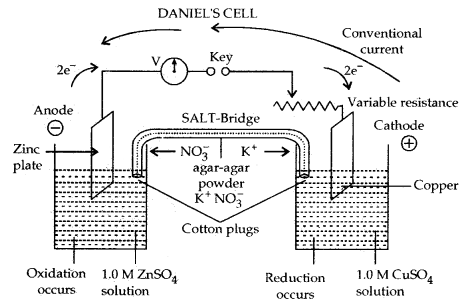
In the left-hand beaker, oxidation occurs. Zn plate dissolves to form Zn²⁺. Zn plate loses weight
Oxidation Half-reaction:
At anode: Zn (s) → Zn²⁺ (aq) + 2e^–

Reduction Half-Reaction: In the right-hand beaker reduction occurs. Cu²⁺ ions from the solution deposit on the copper plate. It gains weight.
At Cathode: Cu²⁺ (aq) + 2e^– → Cu (s)

Electrons flow from zinc plate to copper plate in the external circuit. Conventional current flows from copper to zinc plate (as. shown above) Combining the two half-reactions, we get the complete cell reaction or redox reaction.
Zn (s) + Cu²⁺ (aq) → Zn²⁺ (aq) + 2e^–

Electrolytic Cell: It is a device to convert electrical energy from an external source to produce a chemical change. In the above cell if E_ext is > 1.1. the reaction will again start but in the opposite reaction. It now will function as an electrolytic cell.

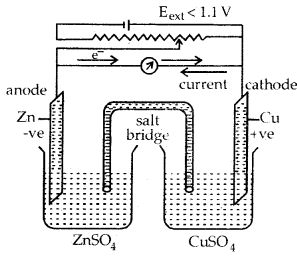
(a) when Eext < 1.1 V

1. Electrons flow from Zn rod to Cu rod hence current flows from Cu to Zn.
2. Zn dissolves at anode and copper deposits at the cathode.

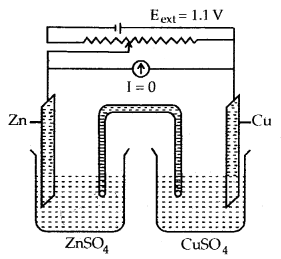
(b) when E_ext = 1.1 V

1. No flow of electrons or current.
2. No chemical reaction.

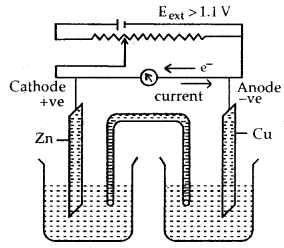
Functioning of Daniell cell when external voltage E_ext opposing the cell potential is applied.
(c) When E_ext > 1.1 V

1. Electrons flow from Cu to Zn arid current flows from Zn to Cu.
2. Zinc is deposited at the zinc electrode and copper dissolves at the copper electrode

In the electrochemical cell at each electrode-electrolyte interface, there is a tendency of metal ions from the solution to deposit on the metal electrode trying to make it positively charged. At the same time, metal atoms of the electrode have a tendency to go into the solution as ions and leave behind the electrons at the electrode trying to make it negatively charged.

At equilibrium, there is a separation of charges and depending on the tendencies of the two opposing reactions, the electrode may be positively or negatively charged with respect to the solution. A potential difference develops between the electrode and the electrolyte which is called Electrode Potential.

When the concentration of all species involved in half-cells is unity, the electrode potential is called Standard Electrode Potential.

According to the IUPAC convention, standard reduction potentials are now called standard electrode potentials. In a galvanic cell, the half¬cell in which oxidation takes place is called Anode and it has a negative potential with respect to the solution. The other half-cell in which reduction takes place is called Cathode and it has a positive potential with respect to the solution. The direction of the flow of current is opposite to that of the flow of electrons.

The cell potential is the difference between the electrode potentials (reduction potentials) of the cathode and anode. It is called electromotive force (emf) of the cell when no current flows through the circuit. Internally the two half-cells/beakers are connected through the salt bridge.
E_cell = E_right – E_left

In the Cu^– AgNO₃ cell cell reaction is
Cu (s) + 2 Ag⁺ (aq) → Cu²⁺ (aq) + 2 Ag (s)
At anode: Cu (s) → Cu²⁺ (aq) + 2 e^–] oxidation
At cathode: 2 Ag⁺ (aq) + 2 e^– → 2Ag (s)] reduction

Here Ag electrode acts as cathode and copper electrode, as anode.
The cell can be represented by
Cu (s) | Cu²⁺ (aq) || Ag⁺ (aq) | Ag (s)
E_cell = E_right – E_left
= E_Ag⁺/Ag – E_Cu²⁺/Cu

Similarly Daxtiel cell can be represented by
Zn (s) | Zn²⁺ (aq) || Cu²⁺ (aq)| Cu (s)
E_cell = E_right – Eleft
= E_Cu²⁺/Cu – E_Zn²⁺/Zn
Measurement of Electrode Potential: The measurement of the potential of half-cells is not possible.

Only the difference between the two half-cell potentials can be determined that gives the e.m.f. of the cell. By arbitrarily fixing the electrode potential of one half-cell, that of the other can be determined.

According to the convention, Standard Hydrogen Electrode represented by Pt (s), H₂(g), H₂(g)/H⁺ (aq) is assigned a zero potential at all temperatures according to the reaction
H⁺(aq) + e^– → H₂(g)

Standard Hydrogen Electrode: It consists of platinum wire sealed in a glass tube arid has a platinum foil attached to it. The foil is coated with finely divided platinum and acts as a platinum electrode. It is dipped into an acid solution containing H⁺ ions in 1 M concentration (1M HCl). Pure H₂ gas at 1 bar pressure is constantly bubbled into the solution at a constant temperature of 298 K. The following reaction occurs in the half-cell depending upon whether it acts as an anode or as a cathode.

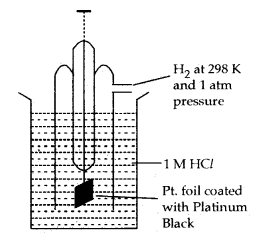
Normal Hydrogen Electrode (NHE)

If S.H.E. (orN.H.E.) acts as Anode
H₂(g) → 2H⁺ (aq) + 2e^– oxidation half reaction

If S.H.E. (or N..H.E.) acts as Cathode
2H⁺ (aq) + 2e^– → H₂ (g)] reduction half reaction

The standard hydrogen electrode is also regarded as a reversible electrode with respect to H+ ions:
H₂(g) ⇌ 2H⁺ (aq) + 2e^–

Arbitrarily, the standard electrode potential of this electrode is fixed to be 0.000 V.
The electrode potential of an electrode can be determined by connecting this half-cell with a standard hydrogen electrode.

The electrode potential of a metal electrode as determined with respect to S.H.E. (or N.H.E.) is called Standard Electrode Potential E°.

Conventionally: The reduction (standard) potential of an electrode that acts as a Cathode when attached to S.H.E. is given a positive sign, e.g., Cu/Cu⁺⁺ electrode when attached to S.H.E. acts as a cathode.

Let us calculate the electrode (reduction) potential of Zn/Zn²⁺. The cell will be
Zn (s) | Zn²⁺_1.0 (aq)| | H⁺ _1.0 (aq), H₂ (g), Pt(s).

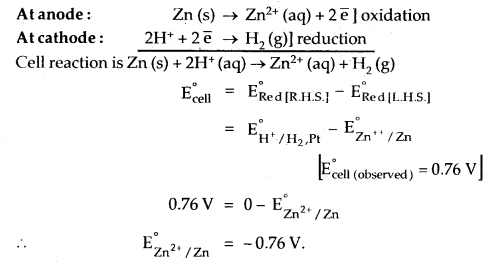
Let us measure the electrode potential of Cu/Cu²⁺ electrode concentration of Cu²⁺ is 1.0 M and the pressure of H₂ gas is one bar. At 298 K, the emf of the cell

Standard hydrogen electrode 11 second half cell.
E°_cell = E°_R – E°_L
0.34 = E°_Cu⁺⁺ – 0 [emf of the cell = 0.34 V]
∴ E_Red° of Cu electrode dipping in Cu²⁺ ions = 0.34 V

Electrochemical Series or The Standard Electrode Potentials at 298 K: Ions are present as aqueous species and H₂O as liquid, gases and solids are shown by aq, g and s.

1. A negative Ev means that the redox couple is a stronger reducing agent than the H⁺/ H₂ couple.
2. A positive Ev means that the redox couple is a weaker reducing agent than the H⁺/H₂ couple.

Applications Of Electrochemical Series:
1. Relative strength of oxidizing and reducing agents: In this series, metals are arranged in the decreasing order of their standard electrode potentials or decreasing order of their oxidizing character. e.g. Li⁺ (aq) which has least reduction potential (- 3.05) is the weakest oxidizing agent and F₂ (g) which has maximum value of p_Red = + 2.85 is the strongest oxidizing agent.

On the other hand, Li metal which has the highest standard oxidation potential (= + 3.05) is the strongest reducing agent while F- ( E°_ox = – 2.85 V) is the least reducing agent.

2. Calculation of e.m.f. of the cell: The e.m.f. of the desired cell can be calculated knowing the standard reducing potentials of the two half cells constituting the cell from the electrochemical series.
E°_cell = E°_Red [RIGHT] – E°Red [LEFT]
e.g. Zn (s) | Zn²⁺ (1.0 M) || Cu²⁺ (1.0 M) | Cu (s).
E°_cell = E°_Cu²⁺,_Cu – E°_Zn²⁺,_Zn.
= 0.34 – (- 0.76) V = 1.10 V

3. Predicting feasibility of redox reaction: In general, a redox reaction is feasible only if the species which has higher standard reduction potential is reduced i.e., accepts the electrons and the species which has lower reduction potential is oxidized i.e., loses the electrons. Otherwise, a redox reaction is not feasible. In other words, the species to release the electrons must have lower reduction potentials as compared to the species which is to accept electrons. In a nutshell, if the e.m.f. of the hypothetical cell is +ve, a redox reaction takes place; if it is – ve, a redox reaction is not feasible.

4. To predict whether a metal can librate H₂(g) from acid or not. The metals which have only negative reduction potentials, i.e., are lying above N.H.E. in the electrochemical series, can only liberate H₂ (g) from dilute acid solutions.

Nernst Equation: The relationship between electrode potentials and the concentration of the electrolytic solutions is called Nernst Equation.
1. The Nernst Equation is
E = E° + \(\frac{\mathrm{RT}}{\mathrm{nF}}\) In [Mn+]/[M] Since[M] = 1
E = E° + \(\frac{2.303 \mathrm{RT}}{\mathrm{nF}}\) log [Mn+]
E = reduction electrode potential
E° = reduction electrode potential in standard state [1 M solution of metal ions at 298 K]
R = Gas constant = 8.314 JK-1.M0l-1
T = Temperature
n = no. of electrons accepted during the change
| F | = Faraday t = 96500 C.

Putting the values of R, T = 298 K; F
| E | = E° + \(\frac{0.059}{\mathrm{n}}\) log [Mn+]

For the complete cell reaction
Zn (s) + Cu²⁺(aq) ⇌ Zn²⁺ (aq) + Cu (s)

2. Calculation of Gibbs free energy/Maximum work that can be obtained from the Galvanic cell
ΛG° = – n F E°elI = – 2.303 RT log Kc
where AG° is the standard Gibbs energy change in Gibbs function
n = number of moles of electrons involved in the cell reaction
F = Faraday = 96,500 coulombs
R = Gas Constant
Kc = Equilibrium constant.

Conductance of Electrolytic Solutions:
Resistance R (ohm) = \(\frac{\text { Potential Difference in volts }}{\text { Current strength in amperes }}\)

Resistance can be measured by the principle of the Wheatstone bridge. It depends upon the length and inversely on the area of cross-section A of the wire.
R ∝ l
R ∝ \(\frac{l}{\mathrm{~A}}\)
or
R = ρ\(\frac{l}{\mathrm{~A}}\);
where ρ (rho) is called specific resistance/Resistivity.

The resistivity of a substance is its resistance to the passage of electricity when it is one metre long and its area of cross-section is one m2.

The inverse of resistance R is called conductance.
Conductance = \(\frac{1}{\mathrm{R}}=\frac{\mathrm{A}}{\rho l}=\frac{\mathrm{A} \kappa}{l}\) ( κ = Kappa)

The SI unit of conductance is Siemens.
1S = 1 ohm^-1 = mho = Ω^-1.

The inverse of resistivity is called Conductivity or Specific Conductance.
SI unit of conductivity is Sm-1, but often (Greek Kappa) is expressed in S cm^-1.

The magnitude of conductivity varies a great deal and depends upon the nature of the material. It also depends upon the temperature and pressure of measurement.

Materials are classified as

1. Conductors,
2. Insulators,
3. Semi-conductors depending upon the magnitude of their conductivity.

Metals and their alloys have very large conductivity and are known as conductors. Certain, non-metals like carbon black, graphite and some organic polymers are also electronically conductors. Substance like glass, ceramics etc. have very low conductivity are known as insulators. Substance like silicon, doped silicon, gallium arsenide is semi-conductors. Electrical conductance ( through metals called metallic or electronic conductance is due to the flow of mobile electrons.

The metallic conductance depends upon,

1. The nature and structure of the metal.
2. The number of valence electrons per atom.
3. Temperature. It decreases with an increase in temperature.
4. The composition of the metallic conductor remains unchanged.

Electrolytic or Ionic Conductance: When electrolytes are dissolved in water, they furnish their own ions in the solution. They conduct electricity through their ions in the solution and is called electrolytic or ionic conductance.

The conductivity of electrolytic or ionic solutions depends upon:

1. The nature of the electrolyte added
2. Size of the ions produced and their solvation.
3. The nature of the solvent and its viscosity.
4. The concentration of the electrolyte.
5. Temperature conductivity increases with an increase in temperature.
6. It leads to a change in its composition with the passage of direct current through the solution over a prolonged period.

Measurement of Conductivity of Ionic Solutions: It is based upon the measurement of resistance by a wheat stone bridge. The cell is called a conductivity cell.

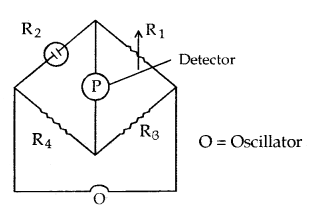
Unknown resistance of the cell R2 = \(\frac{\mathrm{R}_{1} \mathrm{R}_{4}}{\mathrm{R}_{3}}\)
Conductance C of the cell = \(\frac{1}{\mathrm{R}_{2}}\)

Cell Constant = \(\frac{\text { Specific conductance }}{\text { Observated conductance }}\)

Molar Conductivity: It is the conducting power of all ions obtained by dissolving 1 mole of an electrolyte in a given volume of the solution,

Molar conductivity = Λm = \(\frac{x}{c}\)
= \(\frac{\mathrm{Sm}^{-1}}{1000 \mathrm{Lm}^{-3} \times \text { molarity }\left(\mathrm{mL}^{-1}\right)}\)
= S m² mol^-1

Variation of Conductivity and Molar Conductivity with concentration: Both conductivity and molar conductivity change with the concentration of the electrolyte. Conductivity always decreases with the decrease in concentration both for weak and strong electrolytes. This can be explained by the fact that the number of ions per unit volume that carry the current in a solution decreases on dilution. The conductivity of a solution at any given concentration is the conductance of one unit volume of solution kept between two platinum electrodes with a unit area of cross-section and at a distance of unit length. This is clear from the equation:

C = \(\frac{\mathrm{κA}}{l}\)= κ (both A and l are unity in their appropriate Units in m or cm)

Molar conductivity of a solution at a given concentration is the conductance of volume V of a solution containing one mole of electrolyte kept between two electrodes with an area of cross-section A and distance of unit length. Therefore,
Λ_m = \(\frac{\mathrm{κA}}{l}\)= κ
Since l = 1 and A = V (volume containing 1 mole of electrolyte)
Λ_m = κV

Molar conductivity increases with a decrease in concentration. This is because the total volume, V, of a solution containing one mole of electrolyte also increases. It has been found that a decrease in κ on dilution of a solution is more than compensated by an increase in its volume.

Physically, it means that at a given concentration, Λm can be defined as the conductance of the solution of an electrolyte kept between the electrodes of a conductivity cell at a unit distance but having an area of cross-section large enough to accommodate sufficient volume of solution that contains one mole of the electrolyte. When concentration approaches zero, the molar conductivity is known as limiting molar conductivity and is represented by the symbol Λ°_m The variation in Λm with concentration is different for strong and weak electrolytes.

Strong Electrolytes: For strong electrolytes, A increases slowly with dilution and can be represented by the equation :
Λ_m = Λ°_m – A c^1/2
It can be seen that if we plot Λm against c^1/2, we obtain a straight line with an intercept equal to and slope equal to ‘A’. The value of the constant ‘A’ for a given solvent and temperature depends on the type of electrolyte i.e., the charges on the cation and anion produced on the dissociation of the electrolyte in the solution. Thus, NaCl, CaCl₂, MgS04 are known as 1-1, 2-1 and 2-2 electrolytes respectively. All electrolytes Of a particular type have the same value for ‘A’.

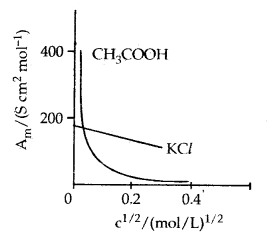
Molar conductivity versus c^1/2 for acetic acid (weak electrolyte) and potassium chloride (strong electrolyte) in aqueous solutions.

Kohlrausch law of independent migration of ions. The law states that limiting molar conductivity of an electrolyte can be represented as the sum of the individual contributions of the anion and cation of the electrolyte. Thus, if λ°_Na and λ°_Cl^– are limiting molar conductivity of the sodium and chloride ions respectively, then the limiting molar conductivity for sodium chloride is given by the equation :
Λ°_m(NaCl) = λ°_Na + λ°_Cl^–

In general: Λ°_m = v₊ λ°₊ + n_– λ°_–
Here λ°₊ and λ°_– are the limiting molar conductivities of the cation and anion respectively.

Weak Electrolytes: Weak electrolytes like acetic acid have a lower degree of dissociation at higher concentration and hence for such electrolytes, the change in Λ_m with dilution is due to an increase in the degree of dissociation and consequently the number of ions in the total volume of solution that contains 1 mol of electrolyte. In such cases, Λ_m increases steeply on dilution, especially near lower concentrations.

Therefore, Λ°m cannot be obtained by extrapolation of Λm to zero concentration. At infinite dilution (i.e., concentration c → zero) electrolyte 5 dissociates completely (α = 1), but at such low concentration, the conductivity of the solution is so low that it cannot be measured accurately. Therefore, Λ°_m for weak electrolytes is obtained by using Kohlrausch law of independent migration of ions. At any concentration c, if a is the degree of dissociation then it can be approximated to the ratio of molar conductivity A m at the concentration c to limiting molar conductivity, Λ°_m.

Thus we have:
α = \(\frac{\Lambda_{\mathrm{m}}}{\Lambda_{\mathrm{m}}^{\circ}}\)
But we know that for a weak electrolyte like acetic acid,

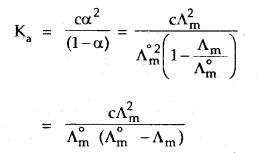
Applications of Kohlrausch law: Using Kohlrausch law of independent migration of ions, it is possible to calculate Λ°_m for any electrolyte from the λ° of individual ions. Moreover, for weak electrolytes like acetic acid, it is possible to determine the value of its dissociation constant once we know the Λ°_m and Λ_m at a given concentration c

Electrolytic Cells and Electrolysis: In an electrolytic cell external source of voltage is used to bring about a chemical reaction. The electrochemical processes are of great importance in the laboratory and the chemical industry. One of the simplest electrolytic cells consists of two copper strips dipping in an aqueous solution of copper sulphate. If a DC voltage is applied to the two electrodes, then Cu²⁺ ions discharge at the cathode (negatively charged) and the following reaction takes place:
Cu²⁺ (aq) + 2e^– → Cu (s)
Copper metal is deposited on the cathode. At the anode copper is converted into Cu²⁺ ions by the reaction:
Cu (s) → Cu²⁺ (s) + 2e^–

Thus copper is dissolved (oxidised) at the anode and deposited (reduced) at the cathode. This is the basis for an industrial process in which impure copper is converted into the copper of high purity. The impure copper is made an anode that dissolves on passing current and pure copper is deposited at the cathode.

Many metals like Na, Mg, Al, etc. are produced on large scale by electrochemical reduction of their respective cations where no suitable chemical reducing agents are available for this purpose. Sodium and magnesium metals are produced by the electrolysis of their fused chlorides and aluminium is produced by electrolysis of aluminium oxide in presence of cryolite.

Faraday’s Laws of Electrolysis:
1. First Law: The amount of chemical reaction which occurs at any electrode during electrolysis by a current is proportional to the quantity of electricity passed through the electrolyte (solution or melt).

2. Second Law: The amounts of different substances liberated by the same quantity of electricity passing through the electrolytic solution are proportional to their chemical equivalent weights (Atomic Mass of Metal. Number of electrons required to reduce the cation).

Some Commercial Cells: The electrochemical cells can be used to generate electricity and these are called batteries. The battery is generally used for two or more galvanic cells connected in series.

There are two types of commercial cells:

1. Primary cells, in which electrode reactions cannot be reversed by external energy source. Therefore, these are not chargeable. For example, dry cell, mercury cell.
2. Secondary cells are those which can be recharged. For example, lead storage cell, nickel-cadmium cell.

→ Fuel Cells: These are voltaic cells in which the reactants are continuously supplied to the electrodes. These are designed to convert the energy from the combustion of fuels such as H₂, CO, CH₄ etc. directly into electrical energy. A common example is a hydrogen-oxygen fuel cell.

→ Corrosion: The process of deterioration of a metal as a result of its reaction with air or water surrounding it is called corrosion. In the case of iron, corrosion is called rusting. Chemically rust is a hydrated form of ferric oxide, Fe₂O₃ x H₂O. It is caused by moisture, carbon dioxide and oxygen present in the air.

The chemistry of corrosion is essentially an electrochemical phenomenon. At a particular spot of an iron object, oxidation takes place and that place behaves as an anode:
Anode 2 Fe(s) → 2Fe²⁺ + 4e^– E°_Fe²⁺/Fe = – 0.44 V

Electrons released at anodic spot move through the metal and go to another spot on the metal and reduce oxygen in presence of H⁺ (which is believed to be .available from H2C03 formed due to dissolution of carbon dioxide from the air into water. Hydrogen ion in water may also be available due to the dissolution of other acidic oxides from the atmosphere).

This spot behaves as cathode with the reaction Cathode:
O₂(g) + 4H⁺ (aq) + 4e^– → 2 H₂O
E_H⁺|O2|H2O = 1.23V

The overall reaction being:
2Fe(s) + O₂(g) + 4H⁺ (aq) → 2Fe₂ (aq) + 2 H₂O (l)
E^V_cell = 1.67 V

The ferrous ions are further oxidised by atmospheric oxygen to ferric ions which come out as rust in the form of hydrated ferric oxide (Fe₂O₂ . x H₂0) and with further production of hydrogen ions.

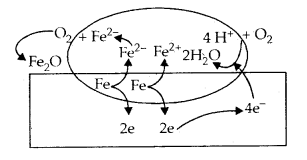
Corrosion of iron in the atmosphere

Oxidation: Fe (s) → Fe²⁺ (aq) + 2e^–
Reduction: O₂(g) + 4H⁺ (aq) + 4e^– → 2H₂O (1)

Atmospheric
oxidation : 2 Fe²⁺ (aq) + 2H₂O (l) + 1/2 O₂ (g) → Fe₂O₃ (s) + 4H⁺ (aq)

Prevention of Corrosion: The rusting of iron can be prevented or decreased by the following methods:
1. Barrier protection: In this method a barrier is placed between the iron and the atmospheric air by coating the surface with paint, applying a thin film of oil or grease or electroplating.

2. Sacrificial protection: In this method, iron is protected by covering it with a layer of metal more active than iron such as zinc, tin, etc. The process of covering iron with zinc is called galvanization.

3. Electrical protection: In this method, the iron is connected with a more active metal like magnesium or zinc.

4. Using anti-rust solution: To retard the corrosion of iron certain anti-rust solutions such as alkaline phosphates and alkaline chromates are used.

Commercial Production of Chemicals: Many metals and their compounds are prepared by using basic principles of electrolysis:

Na is prepared by the electrolysis of molten Na⁺ Cl^– by Down’s Cell

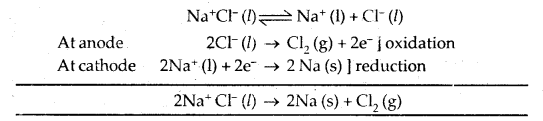
Mg is prepared from fured Mg Cl₂
MgCl₂(Z) ⇌ Mg²⁺ (l) + 2 Cl^– (l)
At anode 2Cl^– → Cl₂ (g) + 2e^–
At cathode Mg²⁺ + 2e^– → Mg (s).

The Hydrogen Economy: Both the production of hydrogen by electrolysis of water
2 H₂O (l) → 2H₂ (g) + O₂ (g) and hydrogen combustion in a fuel cell
2 H₂ (g) + O₂ (g) 2H₂O (l). will be important in future. Both are based on electrochemical principles.