By going through these CBSE Class 12 Chemistry Notes Chapter 4 Chemical Kinetics, students can recall all the concepts quickly.
Chemical Kinetics Notes Class 12 Chemistry Chapter 4
Thermodynamics tells us about the feasibility of a reaction. A reaction is feasible if ΔG < 0 at constant temperature and pressure. Chemical equilibrium tells us the extent to which a reaction can proceed. But none of them tell us the speed of a reaction, i.e., time taken by a reaction to reach equilibrium.
The branch of chemistry which deals with the rates of reactions and their mechanisms is called Chemical Kinetics.
Rate Of A Chemical Reaction
From a kinetics point of view, reactions can be classified into 3 categories:
1. Very fast reactions: Which take place instantaneously e.g., ionic reactions like
AgNO3 (aq) + NaCl (aq) → ↓AgCl (s) + NaNO3 (aq)
BaCl2 (aq) + H2SO4 (aq) → BaS04 (s) + 2 HCl (aq)
NaOH (aq) + HCl (aq) → NaCl (aq) + H2O (l)
2. Very slow reactions: Which may take days or months for
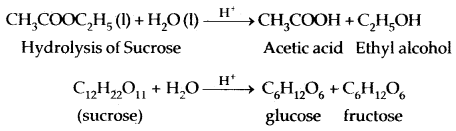
Decomposition of NH4NO2
![]()
Decomposition of Hydrogen peroxide
![]()
Rate Of A Chemical Reaction: The rate of the reaction means the speed of the reaction.
It is defined as the change in the concentration of any one of the reactants or products per unit time.
Rate of the reaction = \(\frac{\text { Decrease in the concentration of a reactant }}{\text { Time taken }}\)
= \(\frac{\text { Increase in the concentration of a product }}{\text { Time taken }}\)
Consider a hypothetical reaction, R → P assuming the volume of the system is constant. One mole of reactant R produces one mole of the product P. If [R]1 and [P]1 are the concentrations of R and P at time t1 and [R]2 and [P]2 are their concentrations at time t2 then
ΔT = t2 – t1
Δ[R] = [R]2 – [R]1
Δ[P] = [P]2 – [P]1
The square brackets are used to express molar concentrations.
Rate of disappearance of R = – \(\frac{\Delta[\mathrm{R}]}{\Delta \mathrm{t}}\) …….(i)
Rate of appearance of P = + \(\frac{\Delta[\mathrm{P}]}{\Delta \mathrm{t}}\) ………(ii)
Equations (i) and (ii) given above represent the average rate of a. reaction, rave. rave depends upon (a) change in the cone, of reactants or products and (ii) time taken for that change to occur.
Units of Rate of a Reaction: Units of rate are concentration time-1, i.e., mol L-1 S-1. However for gaseous reactions, when the concentrations are expressed in terms of partial pressure, then the units of the rate will be atm s-1.
For example,
PCl5 → PCl3 + Cl2

Any general reaction
A + B → C + D

For this reaction, the rate of decomposition (disappearance) of
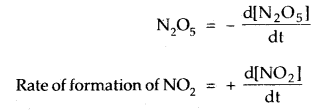
Rate of formation of O2 = + \(\frac{\mathrm{d}\left[\mathrm{NO}_{2}\right]}{\mathrm{d} \mathrm{t}}\)
Rate law: The dependence of the concentration of reactants on the rate of reaction is given by the law. It gives the experimental dependence on concentration of reactants. For example, for the reaction
aA + bB → Products
From the kinetic study of the reaction, the dependence of the concentration of reactants on the rate of the reaction has been found to be
Rate = k[A]m[B]n
where m and n are constant numbers or the powers of the concentration terms of the reactants A and B respectively on which the rate of reaction depends. It may be noted that the values of m and n are determined experimentally and may or may not be equal to a and b coefficients in the reaction. The above expression is the rate law. It may be defined as:
The mathematical expression denotes the observed or actual rate of a reaction in terms of the molar concentration of the reacting species which influences the rate of the reaction.
Order And Molecularity Of A Reaction:
Order of a Reaction: The dependence of reaction rate on concentration may be expressed in terms of the order of a reaction. The order of a reaction is defined as
the sum of the powers to which the concentration terms in the rate law are raised to express the observed rate of a reaction.
Thus, if the rate of a reaction,
xA + yB + zC → Products is given by the rate law,
Rate = –\(\frac{\mathrm{d} \mathrm{x}}{\mathrm{dt}}\) = k[A]x [B]y [C]z then, the order of the reaction, n is
n = x + y + z
where x, y and z are the order with respect to individual reactants and overall order of the reaction is sum of these exponents, i.e., x + y + z.
For example,
1. decomposition of ammonium nitrite is a first-order reaction.
NH4NO2 → N2 + 2H2O
Rate = k [NH4NO2] Order = 1
2. decomposition of hydrogen iodide is a second order reaction
2HI → H2 + I2
Rate = k[HI]2 Order = 2
3. the reaction between nitric oxide and oxygen is a third-order reaction.
2NO (g) + O2 (g) → 2NO2 (g)
Rate = k[NO]2[O2] Order = 3
The order of a reaction may be fractional or even zero.
For example,
CH3CHO → CH4 + CO
Rate = k[CH3CHO]3/2 Order = 3/2
![]()
Rate = k [NH3]° Order = 0
Molecularity of Reaction: The molecularity of a reaction is defined as the number of reacting molecules that collide simultaneously to bring about a chemical reaction.
For example, the decomposition of H2O2 involves only one molecule, so it is a unimolecular reaction.
H2O2 → H2O + \(\frac{1}{2}\)O2
Dissociation of hydrogen iodide is a biomolecular reaction.
2HI (g) → H2 (g) + I2 (g)
The reaction involving three or more than three molecules is uncommon because the occurrence of such reactions would require simultaneous collisions of three or more than three molecules. The chances of the occurrence of such collisions are very small.
However, some of these reactions are found to be quite fast. This means that even though the balanced equation involves a large number of molecules, yet the reaction does not proceed by the simultaneous collision of all these reacting particles.
Such types of reactions take place through a sequence of two or more consecutive steps and are called complex reactions. The detailed description of various steps by which reactants change into the products is called the mechanism of the reaction. The steps which contribute to the overall reaction are called elementary processes.
Mechanism and Rate Law: In the case of multi-step reactions, some of the steps will be very fast while others will be slow. If one step takes place much more slowly than all other steps, it controls the overall reaction rate. This means that all the steps have to wait for the occurrence of this slowest step. But once this slowest step has occurred, the other steps will take place to form the products. In other words, the rate of the reaction is determined by the slowest step in the sequence.
Let us consider reaction between NO2 and F2 to form NO2F;
2NO2(g) + F2(g) → 2NO2F(g)
The experimental observations reveal that the rate of the reaction is proportional to the product of the concentrations of nitrogen peroxide and fluorine. This indicates that the rate-determining step in the mechanism of this reaction must be the reaction between NO2 and F2 only. Keeping this in mind, a mechanism of this reaction may be suggested as:
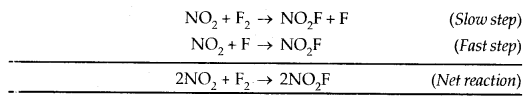
The rate of the overall reaction is determined by the first step which is the slower of the two steps. Accordingly, the experimentally observed rate of the reaction is given by the expression :
fix
Rate = – \(\frac{\mathrm{d} x}{\mathrm{dt}}\) = k[NO2][F2]
The above is the rate law for the reaction. It is, therefore, evident that complex reactions involving more than three molecules in the stoichiometric equation must take place in more than one step.
e.g.KClO3 + 6 FeSO4 + 3 H2SO4 → KCl + 3Fe2 (SO4)3 + 3H2O
should be, apparently, of the tenth order is actually a second-order reaction. This shows that the reaction occurs in several steps. The slowest step is called the rate-determining step.
Consider
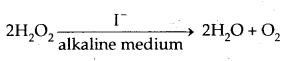
The rate equation for this reaction is found to be
Rate = – \(\frac{\mathrm{d}\left[\mathrm{H}_{2} \mathrm{O}_{2}\right]}{\mathrm{dt}}\) = k [H202][I-]
This reaction is of first order w.r.t. both H2Oz and I-. Evidences suggest that this reaction takes place in 2 steps :
- H2O2 + I → H2O + IO– – Slow Step
- H2O2 + IO– → H2O + I– + O2 – Fast Step
∴ The first step, being slow, is the rate determining step.
It can be concluded from above
- The order of a reaction is an experimental quantity. It can be zero and even a fraction, but molecularity cannot be zero or a non-integer.
- Order is applicable to elementary as well as complex reactions whereas molecularity is applicable only for elementary reactions. For complex reactions, molecularity has no meaning/significance.
- For a complex reaction, the order is given by the slowest step and generally, the molecularity of the slowest step is the same as the order of the overall reaction.
Units of Reaction Rate Constants: The rate is the change in concentration with time. Therefore, the rate of reaction is expressed by concentration units divided by time. If the concentrations are expressed in mol litre-1 and time in seconds, then units of rate constants for different orders are:
- Units for first-order reaction = sec-1
- Units for second-order reaction = litre mol-1 sec-1
- Units for third-order reaction = litre2 mol-2 sec-1
In the case of gaseous reactions, if concentrations are expressed in units of atm, then
- Units of rate constant for the first-order reaction = sec-1
- Units of rate constant for second-order reaction = atm-1 sec-1
- Units of rate constant for third-order reaction = atm-2 sec-1
Rate Constant For First Order Reaction:
For a first-order reaction,
A → Products
Let the initial cone, of [A] be an ML-1.
Let x change into products so that equilibrium concentration after time t is
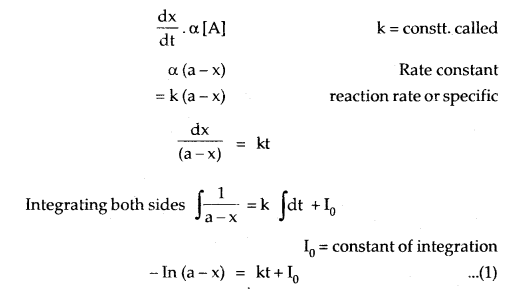
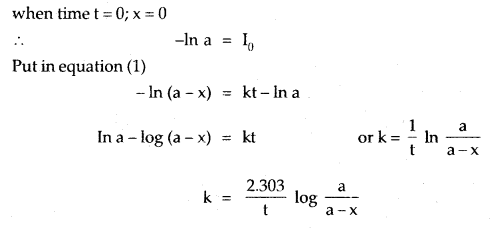
If the initial concentration is ‘a’ moles per liter, x moles of A change in time t and k is the rate constant, then the integrated rate equation is
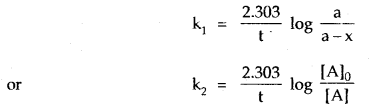
where [A]0 is the initial concentration and [A] is the concentration at time t. The value of k can be calculated by substituting the values of a, t, and x.
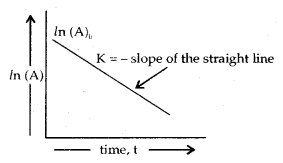
A plot between In (A) and t gives a straight line with a slope equal to – k.
Half-Life Period Of A Reaction: The half-life period of a reaction is defined as the time during which the concentration of a reactant is reduced to one-half of its initial concentration. It is generally denoted as t1/2. The half-life period of a first-order reaction may be calculated as given below:
For the first-order reaction,
t = \(\frac{2.303}{\mathrm{k}}\) log \(\frac{[\mathrm{A}]_{0}}{[\mathrm{~A}]}\)
Now half-life period corresponds to the time during which the initial concentration, [A]0 = a, is reduced to half i.e. [A] = a/2
The half-life period, t1/2becomes
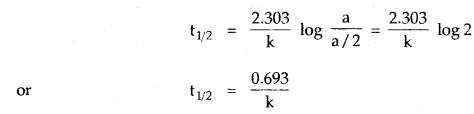
Thus, half life period of a first-order reaction is independent of the initial concentration of the reactant.
Similarly, the relation for the time required to reduce the concentration of the reactant to any fraction of the initial concentration can be calculated. For example,
∴ t3/4 = \(\frac{2.303}{\mathrm{k}}\) log \(\frac{\mathrm{a}}{\mathrm{c} / 4}\) = \(\frac{2.303}{\mathrm{k}}\) log 4
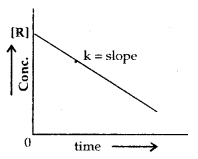
Zero order Reactions are those reactions in which the rate of the reaction is proportional to zero power of the concentration of the reactants.
Rate = – \(\frac{\mathrm{d}[\mathrm{R}]}{\mathrm{dt}}\) = k[R]o = k
or
R = \(\frac{[\mathrm{R}]_{0}-[\mathrm{R}]}{\mathrm{t}}\)
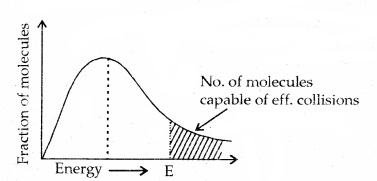
Collision Theory of Reaction Rate: The number of collisions that take place per second per unit volume of the reaction mixture is known as collision frequency (Z). All the collisions are not effective and do not give products. The collisions which actually produce the products and therefore, result in chemical reactions are called effective collisions.
There are two conditions for effective collisions.
1. Energy barrier: For the reacting species to make effective collisions, they should have sufficient energy to break the chemical bond in the reacting molecules. The minimum amount of energy that the colliding molecules must possess is known as threshold energy. Thus, only those collisions of reactants will give products that possess energies greater than threshold energy.
2. Orientation barrier: The colliding molecules should also have proper orientation so that the old bonds may break and new bonds are formed.
Thus, the collisions in which the colliding molecules do not possess the threshold energy of proper orientation do not form products. Therefore, only a small fraction of collision is effective.
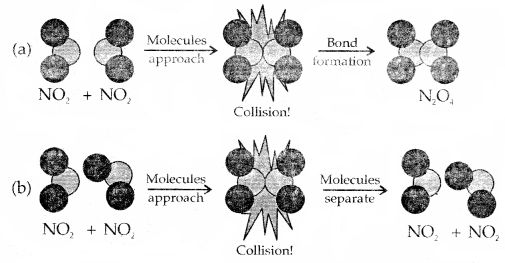
Orientation of colliding NO2 molecules is proper in (a) but ‘not’ in (b) for the reaction to take place.
Dependance Of Reaction Rate On Temperature: Temperature has a great influence on reaction rates. In general, the rate of a reaction becomes almost double for every 10° rise in temperature. The increase in reaction rate is not due to an increase in collision frequency but it is due to an increase in the fraction of effective collisions. It has been found that the fraction of effective collisions becomes almost double for a 10° rise in temperature.
Arrhenius Equation: The quantitative relationship between the rate constant and temperature was proposed by Arrhenius known as the Arrhenius equation.
k = A e-Ea/RT
where k is a constant called frequency factor, Ea is the activation energy. If k1 and k2 are rate constants at two different temperatures T1 and T2 respectively then, integrated form of Arrhenius equation is
log\(\frac{\mathrm{k}_{2}}{\mathrm{k}_{1}}=\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}\left[\frac{\mathrm{T}_{2}-\mathrm{T}_{1}}{\mathrm{~T}_{1} \mathrm{~T}_{2}}\right]\)
Activation Energy: The excess of energy (over and above the average energy of the reactants) required by the reactants to undergo chemical reactions is called activation energy. It is equal to the difference between threshold energy needed for the reaction and the average energy of reactant molecules.
Activation Energy = Threshold energy – Average energy of all reacting molecules.
When the molecules possess the energy equal to E , the atomic configuration of species formed at this stage is different from the reactants as well as the products. This stage is called the activated state or the transition state and specific configuration of the state is called Activated Complex. For example in the reaction between H2 (g) and I2 (g), activated complex has configuration in which H-H arid 1-1 bonds are breacking and H-I bonds are forming as shown below.
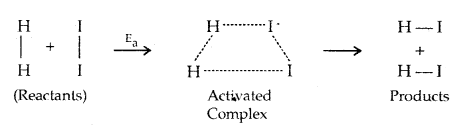
The change of reactants to products, i.e., progress of a reaction is shown below.
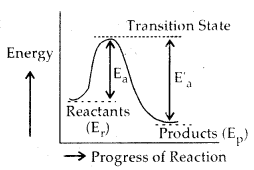
Ea = Activation energy for forward reaction
Ea‘ = Activation energy for backward reaction
Effect Of Catalyst On Reaction Rate:
The substances which increase the rate of a reaction and can be recovered chemically unchanged in mass and composition after the reaction are called catalysts. The phenomenon of increasing the rate of reactions by the use of catalyst is known as catalysis.
The function of a catalyst is that it provides a new path for the reaction, in which the reactants are converted into products quickly. It is believed that the catalyst forms a new activated complex of lower potential energy. This means that the activation energy becomes lower for the catalysed reaction than that for uncatalysed reaction.
Consequently, the fraction of the total number of collisions possessing lower activation energy is increased and hence, the rate of reaction also increases. This is shown below. The solid lines shows the path for uncatalysed reaction and dotted line shows the path adopted by catalysed reaction.
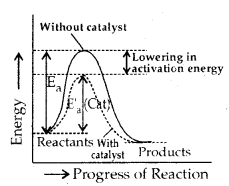
Ea = Activation energy without catalyst
E’a (Cat) = Activation energy with catalyst
Effect Of Radiation On Reaction Rate:
Rate of reaction is increased by use of certain radiations. Such type of reactions which are initiated by the absorption of radiation are called photochemical reactions. For example, reaction of hydrogen and chlorine takes pla,ce very slowly in the absence of light. However, in the presence of light, the reaction occurs rapidly.
![]()
Reversible Reactions: At any stage, the net rate of the reaction is determined by the difference in the rates of forward and backward reactions. At equilibrium the overall rate of reaction in either direction becomes zero. Therefore,
Net rate of reaction = Rate of forward reaction – Rate of backward reaction At equilibrium, net rate is zero, so that
Rate of forward reaction = Rate of backward reaction
For the simple reaction A + B ⇌ C + D
If the rate constant for the forward reaction is Rf and that for the backward reaction is kf then.
Rate of forward reaction a [A] [B] = k [A] [B]
Similarly, rate of backward reaction a [C] [D] = kb [C] [D]
∴ At equilibrium rate of forward reaction = rate of backward reaction
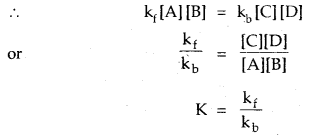
where K = Equilibrium constant
Thus, K = \(\frac{[C] \times[D]}{[A] \times[B]}\)