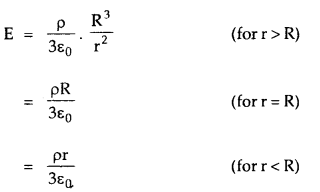By going through these CBSE Class 12 Physics Notes Chapter 1 Electric Charges and Fields, students can recall all the concepts quickly.
Electric Charges and Fields Notes Class 12 Physics Chapter 1
→ The charge on an electron and proton is called a fundamental charge.
→ Electric charge is quantized and charge on a body can be expressed as, q = ± ne, where n is an integer and e = 1.6 × 10-19 C.
→ The minimum value of the dielectric constant is 1 for free space.
→ The maximum value of the dielectric constant is infinity for conductors i.e., metals.
→ A dielectric constant is a dimensionless number as it is the ratio of two similar quantities.
→ Electric charge is a scalar quantity.
→ Electric charge obeys the law of conservation of charge.
→ It is always additive in nature.
→ Coulomb’s law in vector form is more informative than in its scalar form.
→ The electrostatic force is a central force as it acts along the line joining the centers of two charges.
→ The electrostatic force is Newtonian force i.e., obey’s Newton’s third law of motion.
→ Static electricity or frictional electricity on bodies occurs mainly due to the transfer of electrons from one body to another body.
→ 1 C = 3 × 109 stat Coulomb.
→ Stat Coulomb is the C.G.S. unit of charge. It is also called an electrostatic unit (e.s.u.) of charge.
→ S.I. unit of the electric field is NC-1.
→ The dielectric constant is also known as the relative permittivity of the medium (sr).
→ Two equal and opposite charges separated by a finite distance constitute an electric dipole.
→ S.I. Unit of dipolemoment is Coulomb metre (Cm).
→ Electric dipole moment is a vector quantity acting from – q to + q charge.
→ In a uniform electric field, the net force on the dipole is zero and it experiences a torque only,
→ In a uniform electric field, a dipole has only rotatory motion.
→ In a non-uniform electric field, the dipole experiences both torque and force, hence it has rotatory as well as translatory motion.
→ Electric lines of force never intersect each other. They always leave or enter the surface of the conductor perpendicularly.
→ The electric field inside a charged or uncharged conductor placed in an external field is always zero.
→ Electric flux is a scalar quantity and its S.l. unit is Nm-2 C-1.
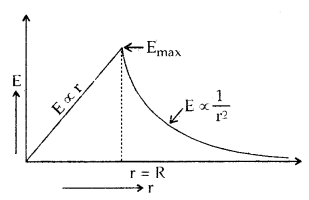
The electric field is maximum at the surface of a charged spherical shell and zeroes inside it.
→ The electric field due to a cloud of charge or due to a solid charged sphere is maximum at its surface and varies with distance from its center as:
→ Electric field lines are perpendicular to the equipotential surface.
→ The surface of a charged conductor is an equipotential surface.
→ Coulomb’s law is valid only for point charges.
→ The electric charge does not change with velocity.
→ No point charge produces an electric field at its own location.
→ Electric charge resides only on the outer surface of a conductor.
→ Coulomb’s force between two charges is independent of the presence of other charges.
→ E is independent of the shape of the conductor.
→ E at a point on the surface of a conductor is directly proportional to the surface density of charge at that point.
→ Eat the center of a charged circular ring is always zero.
→ Coulomb’s law in electrostatics: Two-point charges attract or repel each other with a force directly proportional to the product of the magnitude of charges and inversely proportional to the square of the distance between them.
→ Frictional electricity: Electricity produced on bodies when they are rubbed against each other.
→ Additive nature, of charge: Total charge on an isolated system is equal to the algebraic sum of all individual charges of the system.
→ Law of conservation of charge: Total charge on an isolated system always remains conserved.
→ Principle of superposition: It states that the total force on a given point charge due to other interacting charges is the vector sum of the forces applied by the individual charges on it.
→ Test charge: It is a small +ve charge. It is denoted by q0.
→ Electric field: It is defined as the space around a point charge in which its effect can be felt.
Or
It is the limiting value of electrostatic force per unit test charge
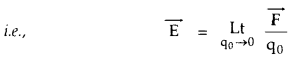
→ Electric dipole: It is a system of two equal and opposite charges separated by a finite distance.
→ Electric dipole moment: It is defined as the product of magnitude. of either charge and the dipole length.
→ Electric line of force: It is defined as the path straight or curved tangent at every point of which gives the direction of the electric field.
→ Electric flux (Φ): It is defined as the total number of electric lines of force passing through an area held normal to them around a given point.
→ Gauss’s law or Theorem: It states that the electric flux through a \(\frac{1}{\varepsilon_{0}}\) closed surface is: times the total charge enclosed inside it.
i.e. Φ = ∮\(\overrightarrow{\mathrm{E}} \overrightarrow{\mathrm{dS}}\) = \(\frac{\mathrm{q}}{\varepsilon_{0}}\)
Gaussian Surface: It is defined as any closed surface around the charge distribution enclosing some charge in it.
Important Formulae:
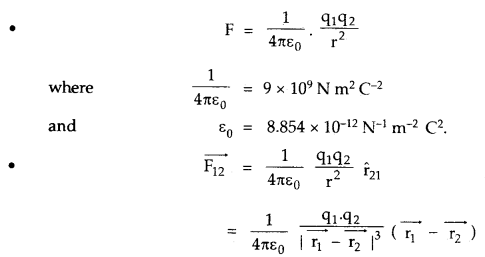
Electric field due to a point charge q is given by
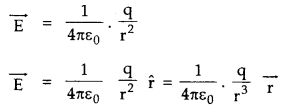
→ The dipole moment of an electric dipole is
\(\overrightarrow{\mathrm{p}}\) = 2 \overrightarrow{\mathrm{a}} q.
→ Electric field at a point on the axis at a distance x from centre of a
charged circular coil of radius r having charge q centre is given by
E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q x}{\left(r^{2}-x^{2}\right)^{3 / 2}}\) alongitsaxis.
→ Electric field at a point on the axial line of an electric dipole at a distance r from its centre is given by
E = \(\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{2 p r}{\left(r^{2}-a^{2}\right)^{2}}\)
= \(\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{2 p}{r^{3}}\) for a short dipole.
→ Electric field at a point on the equitorial line of an electric dipole at a distance r from its centre is given by
E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q x}{\left(r^{2}-x^{2}\right)^{3 / 2}}\)
= \(\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{p}{r^{3}}\) for a short dipole.
→ Torque on an electric dipole in a uniform \(\overrightarrow{\mathrm{E}}\) is
\(\overrightarrow{\mathrm{τ}}\) = \(\overrightarrow{\mathrm{P}}\) × \(\overrightarrow{\mathrm{E}}\)
or
τ = pE sin θ
where θ is the angle between \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{E}}\) .
→ Force on a charge due to n other charges is
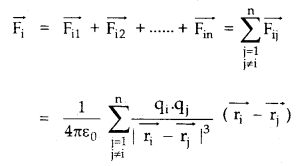
→ Electric flux, = \(\overrightarrow{\mathrm{E}}\). \(\overrightarrow{\mathrm{dS}}\)
When \(\overrightarrow{\mathrm{dS}}\) is the area vector acting alòng outward drawn normal.
Φ = ∮<sub>s</sub> \(\overrightarrow{\mathrm{E}}\) \(\overrightarrow{\mathrm{dS}}\) = \(\frac{\mathrm{q}}{\varepsilon_{0}}\)
→ Electric field at a point due to an infinitely long straight conductor or wire of linear charge density is
E = \(\frac{1}{2 \pi \varepsilon_{0}} \cdot \frac{\lambda}{r}\)
where r = perpendicular distance of the point from the wire,
→ E due to an infinite plane sheet ol charge having surface charge density c is given by
E = \(\frac{\sigma}{2 \varepsilon_{0}}\)
→ E between two plane parallel sheets of charge is given by
E = \(\frac{\sigma}{\varepsilon_{0}}\)
→ \(\overrightarrow{\mathrm{E}}\) at a point due to a spherical shell is
E = \(\frac{\sigma}{\varepsilon_{0}} \cdot \frac{R^{2}}{r^{2}}\) (for r > R)
= \(\frac{\sigma}{\varepsilon_{0}}\) (for r = R)
= 0 for r < R.
When σ = surface charge density.
R = radius of shell.
→ \(\overrightarrow{\mathrm{E}}\) at a point due to a solid sphere of radius R volume charge density p at a point at a distance r is given by