By going through these CBSE Class 12 Physics Notes Chapter 12 Atoms, students can recall all the concepts quickly.
Atoms Notes Class 12 Physics Chapter 12
→ From α-particle scattering, it can be concluded that:
- the atom is mostly neutral.
- the whole of the positive charge is concentrated in a small volume at the center of the atom called the nucleus.
→ In case a proton is moving towards a stationary proton, at the point of the closest approach, the initial kinetic energy of the moving proton is equal to the K.E. of both protons plus the electrostatic potential energy.
→ Wavelength/frequencies/wavenumbers of radiations emitted by the excited H-atom are not continuous.
→ Bohr’s theory is applicable to all one-electron (hydrogenic) atoms
such as He+, Li++, ………..
According to it:
- rn = a0 \(\frac{n^{2}}{Z}\) Å
Where a0 = 0.53 Å = radius of first Bohr’s orbit of the hydrogen atom, - The total energy is negative, so the system is a bound one.
→ B.E. = ground state energy.
→ Ionisation energy = – B. E.
→ If a hydrogen atom in the ground state absorbs a photon of energy hv and is excited to nth state, then
– 13.6 + hv = – \(\frac{13.6}{n^{2}}\)
→ Distance of closest approach (= r0) gives an idea about the size of the nucleus.
→ Spectral lines of the Lyman series are found to lie in the UV region.
→ The longest wavelength of this series (= 1216 Å) is due to 2 → 1
transition.
→ The shortest wavelength of this series (= 912 Å) is due to ∞ → 1 transition.
→ Spectral lines of the Balmer series are found to lie in the visible region
→ Bohr’s model is not applicable to even two-electron atoms such as He.
→ The shortest wavelength of this series (3648 Å) is due to ∞ → 1 transition.
→ 1st, 2nd, 3rd members of this series are called Hα, Hβ, Hγ lines.
→ Spectral lines of the Paschen series lie in the infrared region.
→ The longest wavelength of this series (18761 Å) is obtained due to 4 → 3 transitions.
→ The shortest wavelength of this series (8208 Å) is obtained due to ∞ → 1 transition.
→ Stationary orbits do not mean that the electron is stationary but it means that the energy of the electron remains constant as long as it keeps on moving in the same orbit.
→ When external energy is supplied to the atom, an electron in any orbit absorbs this energy and goes to the higher energy orbit. After 10-8 s, the electron jumps back to the original orbit by emitting the absorbed energy in the form of a photon.
→ The speed of an electron in an orbit is inversely proportional to the
principal quantum number.
→ Ionisation energy of H-atom = E∞ – E1 = = 0 – (- 13.6) = 13.6 eV.
→ The ionization potential of H-atom = 13.6 V.
→ Bohr laid the foundation of the quantum theory by postulating specific orbits in which electrons don’t radiate.
→ Bohr’s model includes only one quantum number n.
→ Bohr modified the Rutherford model of the atom by introducing quantum ideas known as Bohr’s postulates.
→ Rutherford’s atomic model could not explain the stability of the atom.
→ Rutherford concluded that electrons are not stationary but they are moving around the nucleus in circular orbits.
→ Emission or absorption of energy takes place only when an electron jumps from one stationary orbit to the other stationary orbit.
→ The energy of the electron is greater in the outer orbits than in the inner orbit.
→ The energy of the electron for orbit with n = ∞ is maximum and is equal to zero.
→ Spectra is of two types:
- Emission spectrum
- Absorption spectrum.
→ Emission spectrum results when there is the transition from a high energy state to a lower energy state.
→ Absorption spectrum results when energy is absorbed by the atom and goes from a lower energy state to a higher energy state.
→ Fraunhofer’s lines in the sun’s spectra are the absorption lines.
→ There appears a dark line corresponding to photons absorbed in the spectrum.
→ The election may be seen to be at a distance from the nucleus of about 104 to 105 times the size of the nucleus itself. Thus the distance of the closest approach helps us to estimate the size of the nucleus (R).
i. e. r0 = 104 to 105 R.
∴ R = 10-4 to 10-5 r0.
→ Size of atom = 104 to 105 times the size of the nucleus (R).
→ r0 is of the order of size of the atom.
→ The nucleus of gold is about 50 times heavier than an α-particle, thus it (Au nucleus) remains at rest during α-particle scattering.
→ Bohr’s radius: It is the radius of the innermost orbit in the hydrogen atom. It is denoted by r1 or a0.
→ Permitter orbits: They are defined as the orbits for which the angular momentum is an integral multiple of \(\frac{\mathrm{h}}{2 \pi}\) i.e.,
L = mvr = n \(\frac{\mathrm{h}}{2 \pi}\)
→ Impact Parameter: It is the perpendicular distance of the velocity vector of the a-particle from the central line of the nucleus when the particle is far away from the nucleus of the atom.
→ Distance of closest approach: It is the minimum distance up to which an energetic a-particle traveling towards the nucleus can move before coming to rest and then retracing its path.
→ Ground state: It is defined as the energy state of electron corresponding to n = 1.
→ Excited states: They are the energy states of electrons corresponding to n = 2,3, 4. When an electron in the innermost orbit jumps to higher orbits after absorbing the energy.
→ Spectral line: When an electron jumps from a higher energy state to the lower energy state in the hydrogen atom, the radiation of a particular wavelength or frequency is emitted which is called a spectral line.
→ Energy level diagram: The energy of an electron corresponding to each orbit (energy state) can be represented by the horizontal lines.
→ Excitation potential: It is defined as the potential difference through which an electron in an atom must be accelerated so that it may go from the ground state to the excited state. It corresponds to the excitation energy.
→ Excitation: It is the process of absorption of energy by an electron when it goes from a lower energy state to a higher energy state.
→ Ionization: It is the process of detaching or knocking out an electron from the atom.
→ Ionization energy: The energy required to knock out an electron from an atom i.e., from the ground state (n = 1) to energy state n = ∞.
→ Ionization potential: It is defined as the potential difference through which an electron of an atom is accelerated so that it is knocked out of the atom.
Important Formulae
→ Speed of an electron revolving in nth orbit is given by
νn = \(\frac{2 \pi \mathrm{k} \mathrm{Ze}^{2}}{\mathrm{nh}}\)
→ Angular momentum of the electron is given by
m vn rn = \(\frac{\mathrm{nh}}{2 \pi}\)
where vn = Velocity of electron in nth orbit.
rn = radius of orbit of electron in nth orbit,
n = 1, 2, 3, …………..
hv = Ef – Ei
= \(\frac{2 \pi^{2} \mathrm{k}^{2} \mathrm{Z}^{2} \mathrm{me}^{4}}{\mathrm{~h}^{2}}\left(\frac{1}{\mathrm{n}_{\mathrm{i}}^{2}}-\frac{1}{\mathrm{n}_{\mathrm{f}}^{2}}\right)\)
→ Rydberg constant is given by
R = \(\frac{2 \pi^{2} m k^{2} e^{4}}{c h^{3}}\)
→ Velocity in terms of fine structure constant is given by

→ Impact parameter is given by
b = \(\frac{\mathrm{Ze}^{2} \cot \frac{\theta}{2}}{4 \pi \varepsilon_{0} . \mathrm{E}}\)
where θ = angle of scattering.
E = \(\frac{1}{2}\) mv2 = K.E. of α-particle.
→ Ionisation potential is given by
V = \(\frac{13.6 \mathrm{Z}^{2}}{\mathrm{n}^{2}}\)
Where Z = an atomic number of the atom.
n = number of orbit from which electron is to be removed.
→ Rydberg formula for spectrum of H-atom is
\(\bar{v}\) = R\(\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)\)
= wave number of radiation emitted.
→ Ionisation energy of Hydrogen atom is
E = E∞ – E1 = 13.6 eV,
→ Total energy of electron in nth orbit of hydrogen atom is given by
E = – \(\frac{2 \pi^{2} m k^{2} e^{4}}{n^{2} h^{2}}\)
= – \(\frac{13.6}{\mathrm{n}^{2}}\) eV.
→ For H-like atoms
E = \(\frac{13.6}{\mathrm{n}^{2}}\) Z2(eV).
→ The energy of electron in various stationary orbits for H-atom is
E1 = -13.6 eV
E2 = – 3.4 eV
E3 = -1.51 eV
E4 = -0,85eV
E5 = -0.54 eV.
…………………..
…………………..
→ For the Lyman series,
\(\bar{v}\) = \(\frac{1}{λ}\) = R(\frac{1}{1^{2}}-\frac{1}{n^{2}})
→ For Balmer series,
\(\bar{v}\) = \(\frac{1}{λ}\) = R(\frac{1}{Z^{2}}-\frac{1}{n^{2}})
where n = 3, 4, 5, ….n.
→ For Paschen series,
\(\bar{v}\) = \(\frac{1}{λ}\) = R(\frac{1}{3^{2}}-\frac{1}{n^{2}})
where n = 4, 5, 6, …. n.
→ For Pfund series,
\(\bar{v}\) = \(\frac{1}{λ}\) = R(\frac{1}{4^{2}}-\frac{1}{n^{2}})
where n = 5, 6, ….n.
→ radius of nth orbit is given by
rn = \(\frac{n^{2} h^{2}}{4 \pi^{2} m k Z e^{2}}\)
= \(\frac{n^{2} h^{2}}{4 \pi^{2} m k e^{2}}\) for H-atom.
→ K.E. of electron revolving in nth orbit is
Ek = \(\frac{1}{2}\) . \(\frac{\mathrm{kZe}^{2}}{\mathrm{r}_{\mathrm{n}}}\)
for H-atom
Ek = \(\frac{1}{2}\) . \(\frac{\mathrm{ke}^{2}}{\mathrm{r}_{\mathrm{n}}}\)
P.E. of an electron in nth orbit is
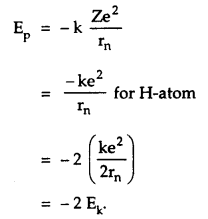
→ Total energy in nth orbit is
E = KE. + P.E.
= Ek – 2Ek
= – Ek = \(\frac{\mathrm{ke}^{2}}{2 \mathrm{r}_{\mathrm{n}}}\)
→ Distance of closest approach is α-particle is given by
r0 = \(\frac{(\mathrm{Ze}) \cdot(2 \mathrm{e})}{4 \pi \varepsilon_{0} . \mathrm{E}}=\frac{2 \mathrm{Ze}^{2}}{4 \pi \varepsilon_{0}\left(\frac{1}{2} \mathrm{mv}^{2}\right)}\)
→ Ionisation potential = \(\frac{\text { ionisation energy }}{\mathrm{e}}\)
→ Excitation potential = \(\frac{\text { excitation energy }}{\mathrm{e}}\)
→ The number of a-particles per unit area that reach the screen at a scattering angle θ are found to vary as:
N(θ) ∝ \(\frac{1}{\sin ^{4}\left(\frac{\theta}{2}\right)}\)