By going through these CBSE Class 12 Physics Notes Chapter 8 Electromagnetic Waves, students can recall all the concepts quickly.
Electromagnetic Waves Notes Class 12 Physics Chapter 8
→ Displacement current is a 1 ways equal to charging (for discharging) current and lasts so long as the capacitor (producing varying electric field) is charged or discharged.
→ An accelerated charged particle emits e.m. waves.
→ \(\overrightarrow{\mathrm{S}}\) = \(\overrightarrow{\mathrm{E}}\) × \(\overrightarrow{\mathrm{B}}\) is called Poynting vector acts in a direction perpendicular to the plane of \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{B}}\) .
→ The displacement current is named so because it is produced by the displacement of electrons caused by changing electric fields.
→ X-rays have the shortest wavelength (≈ 1 Å).
→ The charging or discharging current is called conduction current.
→ The amplitude of electric and magnetic fields in free space in e.m. waves are related as E = CB
→ Electric vector is called light vector as it is responsible for the optical effect of e.m. wave.
→ The energy of the e.m. wave is shared equally between the electric field vector and the magnetic field vector.
→ Microwaves are very commonly used in radar to locate flying objects like airplanes, jet planes, etc.
→ Tire earth’s atmosphere produces Green House effect. In the absence of the earth’s atmosphere, the temperature on earth during the day will increase and during the night it would decrease.
→ The ozone layer which is present in the stratosphere protects the earth from high-energy radiations coming from outer space.
→ The velocity of em. waves in a medium is given by
v = \(\frac{1}{\sqrt{\mu_{0} \varepsilon_{0} \mu_{\mathrm{r}} \varepsilon_{\mathrm{r}}}}=\frac{C}{\sqrt{\mu_{\mathrm{r}} \varepsilon_{\mathrm{r}}}}\)
→ There is no conduction current in a traveling e.m. wave.
→ Earth’s atmosphere is transparent to visible light and most of the infrared rays are absorbed by the atmosphere.
→ Radio waves were discovered by Hertz and are used in communication.
→ e.m. waves are transverse in nature.
→ e.m. waves exert pressure on the objects on which they fall as they carry energy and momentum.
→ The wavelength range of em. waves are from 10-15 m to 109 m and the frequency range is 1024 Hz to 1 Hz.
→ Green House Effect takes place due to the heating of the earth’s atmosphere due to the trapping of infrared rays by the CO2 layer in the atmosphere.
→ Modified Ampere Circuital law: It states that the line integral of the magnetic field around a closed path is always equal to μ0 times the sum of the conduction dnd displacement currents i.e.,
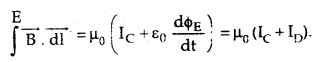
→ Displacement Current: It is defined as the current produced in a region where a change of electric flux takes place due to the change in electric field intensity in that region.
Important Formulae
→ Amper’s circuital law states that
∫ \(\overrightarrow{\mathrm{B}}\).\(\overrightarrow{\mathrm{dl}}\) = μ0 IC
where IC = conduction current Displacement current is given by
→ Displacement current is given by
ID = ε0 \(\frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\)
→ C = \(\frac{E_{0}}{B_{0}}=\frac{1}{\sqrt{\mu_{0} \varepsilon_{0}}}\)
→ Energy density of electric field, UE = \(\frac{1}{2}\) ε0 E2
→ Energy density of electric field, UB = \(\frac{\mathrm{B}^{2}}{2 \mu_{0}^{2}}\)
→ Intensity of e.m. wave is given by
I = average energy density × speed of e.m. wave
= \(\frac{1}{2}\) ε0E2 × C = ρ/4πr²
→ \(\overrightarrow{\mathrm{B}}\) at a point between the plates of the capacitor at a distance r from its axis is given by.
B = \(\frac{\mu_{0} \mathrm{Ir}}{2 \pi \mathrm{R}^{2}}\)
Where R = radius of each circular plate of the capacitor.
→ Velocity of e.m. waves is
C = vλ
→ An electromagnetic wave of frequency v, wavelength λ propagating along the z-axis, we have
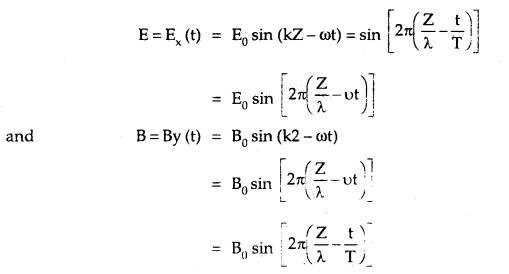
→ The speed of light or of electromagnetic waves in a material medium is given by
υ = \(\frac{1}{\sqrt{\mu \varepsilon}}\)
where μ is the permeability of the medium and ε is its permittivity.
→ Bmax = \(\frac{\mu_{0} I_{D}}{2 \pi R}\)