Electric Charges and Fields Class 12 Important Extra Questions Physics Chapter 1

Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 1 Electric Charges and Fields. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.

Class 12 Physics Chapter 1 Important Extra Questions Electric Charges and Fields

Electric Charges and Fields Important Extra Questions Very Short Answer Type

Question 1.
What is the value of the angle between the vectors \(\vec{p}\) and \(\vec{E}\) for which the potential energy of an electric dipole of dipole moment \(\vec{p}\), kept in an external electric field \(\vec{E}\), has maximum value.
Answer:
P.E. = –pEcos θ
P.E. is maximum when cos θ = – 1, i.e.
θ = 180°

Question 2.
Define electric field intensity at a point.
Answer:
Electric field intensity at a point is defined as the force experienced by a unit test charge placed at that point. Mathematically
we have

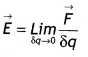
Question 3.
Two equal point charges separated by 1 m distance experience force of 8 N. What will be the force experienced by them, if they are held in water, at the same distance? (Given: K_water = 80) (CBSE Al 2011C)
Answer:
The force in water is given by
F_w = \(\frac{F_{\text {air }}}{K}=\frac{8}{80}\) = 0.1 N

Question 4.
A charge ‘q’ is placed at the center of a cube of side l. What is the electric flux passing through each face of the cube? (CBSE AI 2012) (CBSE Sample Paper 2019)
Answer:
Φ = q/6ε₀

Question 5.
Why do the electric field lines not form closed loops? (CBSE Al 2012C)
Answer:
It is due to the conservative nature of the electric field.

Question 6.
Two equal balls having equal positive charge ‘q’ coulomb are suspended by two insulating strings of equal length. What would be the effect on the force when a plastic sheet is inserted between the two? (CBSE AI 2014)
Answer:
It decreases because force ∝= \(\frac{1}{k}\) and k > 1.

Question 7.
What is the electric flux through a cube of side l cm which encloses an electric dipole? (CBSE Delhi 2015)
Answer:
Zero

Question 8.
Why are electric field lines perpendicular at a point on an equipotential surface of a conductor? (CBSE Al 2015C)
Answer:
So that no net force acts on the charge at the equipotential surface and it remains stationary.

Question 9.
What is the amount of work done in moving a point charge Q. around a circular arc of radius ‘r’ at the centre of which another point charge ‘q’ is located? (CBSE Al 2016)
Answer:
Zero.

Question 10.
How does the electric flux due to a point charge enclosed by a spherical Gaussian surface get affected when its radius is increased? (CBSE Delhi 2016)
Answer:
No change, as flux does not depend upon the size of the Gaussian surface.

Question 11.
Draw the pattern of electric field lines, when a point charge –Q is kept near an uncharged conducting plate. (CBSE Delhi 2019)
Answer:
The pattern is as shown.

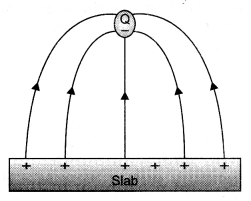
Question 12.
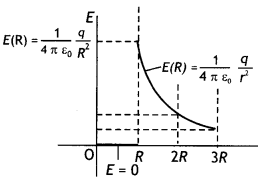
Draw a plot showing the variation of the electric field with distance from the center of a solid conducting sphere of radius R, having a charge + Q on its surface. (CBSE Delhi 2017C)
Answer:
The plot is as shown.

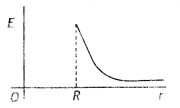
Question 13.
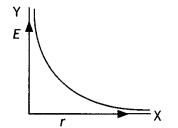
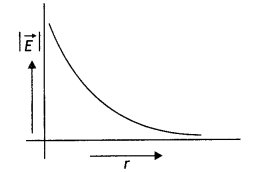
Draw a graph to show the variation of E with perpendicular distance r from the line of charge (CBSE Delhi 2018)
A
Answer:
E = \(\frac{\lambda}{2 \pi \varepsilon_{0} r}\)
E ∝ \(\frac{1}{r}\)

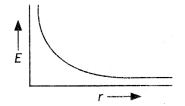
The graph between E and r is as shown.

Question 14.
Define the term ‘electric flux’. Write its S.I. unit. (CBSE Delhi 2018)
Answer:
Electric flux: It is the measure of the number of electric field lines crossing a given area normally.

Mathematically the electric flux passing through an area \(\vec{dS}\) is given by
dΦ = \(\vec{E}\) . \(\vec{dS}\)

SI unit of electric flux is Nm²C^-1 or Vm.

Question 15.
Why can the interior of a conductor have no excess charge in the static situation? (CBSE Ai 2019)
Answer:
Since the electric field inside the conductor is zero, electric flux through the closed surface is also zero. Hence by Gauss’s law, there is no net charge enclosed by the closed surface.

Question 16.
Two field lines never cross each other. Why?
Answer:
It is because at the point of intersection two perpendiculars can be drawn. Thus there will be two directions of the electric field at that point which is not possible.

Question 17.
In an electric field, an electron is kept freely. If the electron is replaced by a proton, what will be the force experienced by the proton?
Answer:
The magnitude of force will be the same but the direction will be reversed.

Question 18.
Consider the situation shown in the figure given below. What are the signs of q₁ and q₂?
Answer:

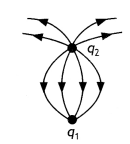
q₁ is negative and q₂ is positive.

Question 19.
In the figure given below, at which point electric field is maximum?
Answer:

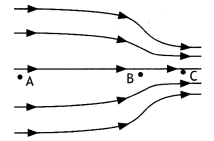
The electric field is maximum at point C.

Question 20.
An uncharged insulated conductor A is brought near a charged insulated conductor B. What happens to the charge and potential of B?
Answer:
On bringing uncharged conductor A near a charged conductor B, charges are induced on A as shown in the figure below. As a result, the potential of conductor B is slightly lowered but the charge on it remains unchanged.

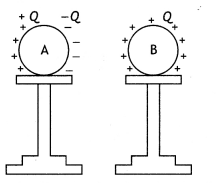
Question 21.
In a medium the force of attraction between two point electric charges, distance ‘d’ apart, is F. What distance apart should these be kept in the same medium so that the force between them becomes 3F?
Answer:
Let the new distance be ‘d’, since F ∝\(\frac{1}{r^{2}}\) ,
therefore \(\frac{F}{3 F}=\frac{r^{2}}{d^{2}}=\frac{1}{3} \Rightarrow r=\frac{d}{\sqrt{3}}\)

Question 22.
Find the value of an electric field that would completely balance the weight of an electron.
Answer:
mg = eE ⇒ E = \(\frac{m g}{e}\)
= \(\frac{9.1 \times 10^{-31} \times 9.8}{1.6 \times 10^{-19}}=5.57 \times 10^{-11} \mathrm{Vm}^{-1}\)

Question 23.
Two charges, one +5 µC, and the other -5 µC are placed 1 mm apart. Calculate the electric dipole moment of the system.
Answer:
p = q × 2a = 5 × 10 ^-6 × 10^-3 = 5 × 10^-9 Cm

Question 24.
Two-point charges of+3 µC each are 100 cm apart. At what point on the line joining the charges will the electric intensity be zero?
Answer:
At the mid-point of the line joining the two point charges.

Question 25.
Four charges of came magnitude and same sign are placed at the corners of a square, of each side 0.1 m. What is electric field intensity at the center of the square?
Answer:
Zero.

Question 26.
Why should the electrostatic field be zero ‘ inside a conductor? (CBSE Delhi 2012)
Answer:
Because it does not contain any charge.

Question 27.
A metallic spherical shell has an inner radius R₁ and outer radius R₂. A charge Q is placed at the center of the shell. What will be the surface charge density on the (i) inner surface, and (ii) the outer surface of the shell? (CBSE Delhi 2018)
Answer:
On inner surface

On the outer surface,

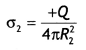
Question 28.
An arbitrary surface encloses a dipole. What is the electric flux through this surface? (NCERT Exemplar)
Answer:
Zero.

Electric Charges and Fields Important Extra Questions  Short Answer Type

Question 1.
(a) Electric field inside a conductor is zero. Explain.
(b) The electric field due to a point charge at any point near it is given as
E  =

what is the physical significance of this limit?
Answer:
(a) By Gauss theorem \(\phi \vec{E} \cdot \overrightarrow{d S}=\frac{q}{\varepsilon_{0}}\). Since there is no charge inside a conductor therefore in accordance with the above equation the electric field inside the conductor is zero.
(b) It indicates that the test charge should be infinitesimally small so that it may not disturb the electric field of the source charge.

Question 2.
Define the electric line of force and give its two important properties.
Answer:
It is a line straight or curved, a tangent to which at any point gives the direction of the electric field at that point.
(a) No two field lines can cross, because at the point of intersection two tangents can be drawn giving two directions of the electric field which is not possible.
(b) The field lines are always perpendicular to the surface of a charged conductor.

Question 3.
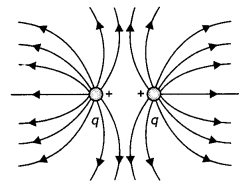
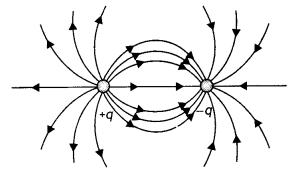
Draw electric field lines due to (i) two similar charges, (ii) two opposite charges, separated by a small distance.
Answer:
(a) The diagram is as shown.

(b) The diagram is as shown.

Question 4.
An electric dipole is free to move in a uniform electric field. Explain what is the force and torque acting on it when it is placed
(i) parallel to the field
Answer:
When an electric dipole is placed parallel to a uniform electric field, net force, as well as net torque acting on the dipole, is zero and, thus, the dipole remains in equilibrium.

(ii) perpendicular to the field
Answer:
When the dipole is placed perpendicular to the field, two forces acting on the dipole form a couple, and hence a torque acts on it which aligns its dipole along the direction of the electric field.

Question 5.
A small metal sphere carrying charge +Q. is located at the center of a spherical cavity in a large uncharged metallic spherical shell. Write the charges on the inner and outer surfaces of the shell. Write the expression for the electric field at the point P₁(CBSE Delhi 2014C)
Answer:

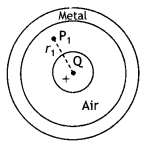
Charge on inner surface – Q.
Charge on outer surface + Q,
Electric field at point P = E = k\(\frac{Q}{r_{1}^{2}}\)

Question 6.
Two-point charges q and –2q are kept ‘d’ distance apart. Find the location of the point relative to charge ‘q’ at which potential due to this system of charges is zero. (CBSE Al 2014C)
Answer:
Let the potential be zero at point P at a distance x from charge q as shown

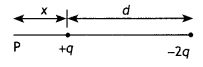
Now potential at point P is
V = \(\frac{k q}{x}+\frac{k(-2 q)}{d+x}\) = 0

Solving for x we have
x = d

Question 7.
Two small identical electrical dipoles AB and CD, each of dipole moment ‘p’ are kept at an angle of 120° as shown in the figure. What is the resultant dipole moment of this combination? If this system is subjected to the electric field (\(\vec{E}\)) directed along +X direction, what will be the magnitude and direction of the torque acting on this? (CBSE Delhi 2011)

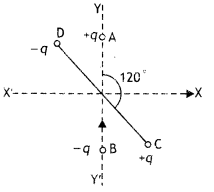
Answer:
The resultant dipole moment of the combi-nation is
P_R = \(\sqrt{p^{2}+p^{2}+2 p^{2} \cos 120^{\circ}}\) = p

since cos 120° = -1/2
This will make an angle of 30° with the X-axis, therefore torque acting on it is
τ=PE sin 30° = pE/2 (Along Z-direction)

Question 8.
A metallic spherical shell has an inner radius R₁ and outer radius R₂. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface? (NCERT Exemplar)
Answer:
The induction of charges is as shown.

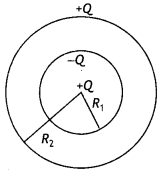
Therefore surface charge density on the inner and the outer shell is on the outer surface is

Question 9.
If the total charge enclosed by a surface is zero, does it imply that the electric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that the net charge inside is zero. (NCERT Exemplar)
Answer:
No, the field may be normal to the surface. However, the converse is true i.e. when the electric field everywhere on the surface be zero then the net charge inside it must be zero.

Electric Charges and Fields Important Extra Questions Long Answer Type

Question 1.
(a) State Gauss theorem in electrostatics. Using it, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
Answer:
It states, “The net electric flux through any Gaussian surface is equal to \(\frac{1}{\varepsilon_{0}}\) times the net electric charge enclosed by the surface.

Mathematically, Φ =\( \phi \vec{E} \cdot d \vec{A}=\frac{q_{i n}}{\varepsilon_{0}}\)

Consider an infinite plane sheet of charge. Let a be the uniform surface charge density, i.e. the charge per unit surface area. From symmetry, we find that the electric field must be perpendicular to the plane of the sheet and that the direction of E on one side of the plane must be opposite to its direction on the other side as shown in the figure below. In such a case let us choose a Gaussian surface in the form of a cylinder with its axis perpendicular to the sheet of charge, with ends of area A.

The charged sheet passes through the middle of the cylinder’s length so that the cylinder’s ends are equidistant from the sheet. The electric field has a normal component at each end of the cylinder and no normal component along the curved surface of the cylinder. As a result, the electric flux is linked with only the ends and not the curved surface.

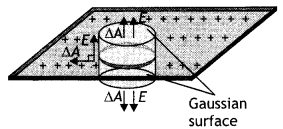
Therefore by the definition of eLectric flux, the flux Linked with the Gaussian surface is given by
Φ = \(\oint_{A} \vec{E} \cdot \vec{\Delta} A\)
Φ = E_A + E_A = 2E_A … (1)

But by Gauss’s Law
Φ = \(\frac{q}{\varepsilon_{0}}=\frac{\sigma A}{\varepsilon_{0}}\) [∵ q = σA] … (2)

From equations (1) and (2), we have
2E_A = \(\frac{\sigma A}{\varepsilon_{0}}\) … (3)
E = \(\frac{\sigma}{2 \varepsilon_{0}}\) …. (4)

This gives the electric field due to an infinite plane sheet of charge which is independent of the distance from the sheet.

(b) How is the field directed if (i) the sheet is positively charged, (ii) negatively charged? (C8SE Delhi 2012)
Answer:
(a) directed outwards
(b) directed inwards.

Question 2.
Use Gauss’s law to derive the expression for the electric field (\(\vec{E}\) ) due to a straight uniformly charged infinite line of charge λ Cm^-1. (CBSE Delhi 2018)
Answer:

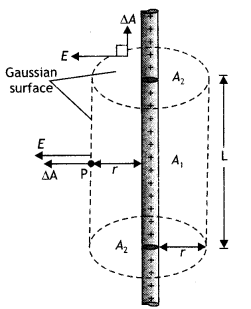
Consider an infinitely Long, thin wire charged positively and having uniform Linear charge density λ. The symmetry of the charge distribution shows that must be perpendicular to the tine charge and directed outwards. As a result of this symmetry, we consider a Gaussian surface in the form of a cylinder with arbitrary radius r and arbitrary Length L. with its ends perpendicular to the wire as shown in the figure. Applying Gauss’s theorem to curved surface ΔA₁ and circular surface ΔA₂.

Φ EΔA1 cos 0°+ EΔA2 cos 90° = \(\frac{q}{\varepsilon_{0}}\) = \(\frac{\lambda l}{\varepsilon_{0}}\) [∵ λ = \(\frac{q}{e}\)]
Or
E . 2πrl = \(\frac{\lambda l}{\varepsilon_{0}}\) ⇒ E = \(\frac{1}{2 \pi \varepsilon_{0}} \frac{\lambda}{r}\)

This is the expression for the electric field due to an infinitely long thin wire.
The graph is as shown.

Question 3.
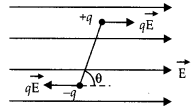
Obtain the expression for the potential energy of an electric dipole placed with its axis at an angle (θ) to an external electric field (E). What is the minimum value of the potential energy? (CBSE 2019C)
Answer:
The torque x acting on an electric dipole of dipole moment p placed in a uniform electric field E is given by:
τ = pEsinθ …(i)
where θ is the angle made by the dipole with the electric field E. The torque tends to align the dipole along the direction of the field. If the dipole is rotated through a small angle dθ against the torque, work has to be done, which is stored in the form of the potential energy of the dipole.

Work done in rotating the dipole through the angle dθ against the torque τ is given by dw = τ dθ = pE sin θ dθ

If the dipole is rotated from θ₁ to θ₂, then
Total work is done,

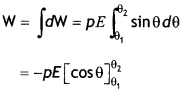
W = – pE(cos θ₂ – cos θ₁)

This work done is stored as potential energy U.

U = – pE(cos θ₂ – cos θ₁)
If the dipole is rotated from θ₁ = \(\frac{\pi}{2}\) to θ₂ =θ, then

U = – pE(cos θ – cos \(\frac{\pi}{2}\) )
= – pE(cos θ – 0)

U = – pE cos θ
minimum value of potential energy
U = – pE When θ = 0°

Question 4.
Why does the electric field inside a dielectric decrease when it is placed in an external electric field?
Answer:
When a dielectric is placed in an electric field (E₀), it gets polarised, i.e. within the dielectric, an electric field (E) is induced in a direction opposite to that of the external field. Therefore, the net field within the dielectric decreases to \(\vec{E}_{0}\) – \(\vec{E}\)

Question 5.
Two-point charges +q and -2q are placed at the vertices ‘B’ and ‘C’ of an equilateral triangle ABC of side ‘a’ as given in the figure. Obtain the expression for (i) the magnitude and (ii) the direction of the resultant electric field at vertex A due to these two charges. (CBSE Al 2014 C)

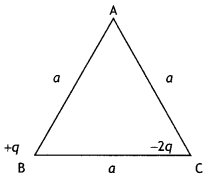
Answer:
The electric fields due to the two charges placed at B and C are inclined at an angle θ = 120° as shown
Now in magnitude, we have

E_B = k\(\frac{q}{a^{2}}\) and
E_C = k\(\frac{2q}{a^{2}}\) = 2 E_B

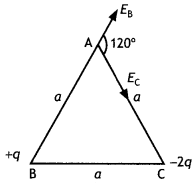
Hence E = \(\sqrt{E_{B}^{2}+E_{c}^{2}+2 E_{B} E_{c} \cos \theta}\)
Or E = \(\sqrt{E_{B}^{2}+\left(2 E_{B}\right)^{2}+2 E_{B}\left(2 E_{B}\right) \cos 120^{\circ}}\)

On Solving we have
E = \(\sqrt{3} E_{B}\) = \(\sqrt{3} \frac{k q}{a^{2}}\)

Direction

Therefore B = 90°, the resultant is inclined at an angle of 90° with EB.

Question 6.
Four-point charges Q, q, Q, and q are placed at the corners of a square of side ‘a’ as shown in the figure.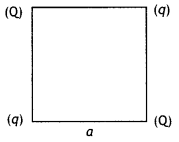
Find the
(a) the resultant electric force on a charge Q and
(b) the potential energy of this system. (CBSEAI, Delhi 2018)
Answer:
(a) Let us find the force on charge Q at point C.

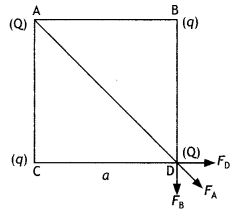
Force due to charge Q placed at point A is
F_A = k\(\frac{Q^{2}}{(a \sqrt{2})^{2}}\) =k\(\frac{Q^{2}}{2 a^{2}}\) along AC

Force due to the charge q placed at D
F_D = k\(\frac{q Q}{a^{2}}\) alongDA

Force due to the charge q placed at B
F_B = k \(\frac{q Q}{a^{2}}\) along BC

The resuLtant of F_D and F_B is
F_BD = K\(\frac{q Q \sqrt{2}}{a^{2}}\) along AC

∴ net force of charge Q placed at point C is

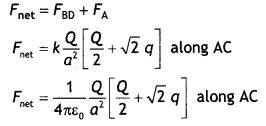
(b) PotentiaL energy of the system

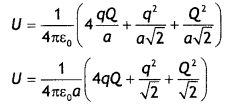
Question 7.
A charge +Q is uniformly distributed within a sphere of radius R. Find the electric field, distant r from the center of the sphere where: (1) r < R and (2) r > R. (CBSEAI 2016C)
Answer:
For a solid sphere p = \( \frac{q}{\frac{4}{3} \pi R^{3}}\) = \(\frac{q}{\text { volume }}\)

Case 1. 0 < r < R The point Lies within the sphere.

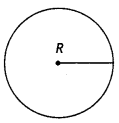
Using Gauss’s theorem
Let Q’ be the charge encLosed by Gaussian’s surface of radius r < R.

E(4πr²)=\(\frac{Q^{\prime}}{\varepsilon_{0}}=\frac{Q^{\prime}}{4 \pi \varepsilon_{0} r^{2}}\)

From (i) and (ii)
E = \(\frac{Q r^{3}}{4 \pi \varepsilon_{0} r^{2} R^{3}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q r}{R^{3}}\)

Case 2. For r > R
\(\oint \vec{E} \cdot \overrightarrow{d s}\) = \(\frac{q_{\text {enclosed }}}{\varepsilon_{0}}\)

E(4πr²) = \(\frac{Q}{\varepsilon_{0}}\)
E = \(\frac{Q}{4 \pi \varepsilon_{0} r^{2}}\)

Question 8.
(a) An electric dipole is kept first to the left and then to the right of a negatively charged infinite plane sheet having a uniform surface charge density. The arrows p₁ and p₂ show the directions of its electric dipole moment in the two cases. Identify for each case, whether the dipole is in stable or unstable equilibrium. Justify each answer.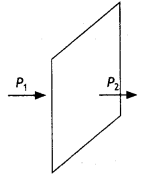
Answer:
p₁: stable equilibrium, p₂: unstable equilibrium. The electric field, on either side, is directed towards the negatively charged sheet and its magnitude is independent of the distance of the field point from the sheet. For position P₁ dipole moment and electric field are parallel. For position p₂, they are antiparallel.

(b) Next, the dipole is kept in a similar way (as shown), near an infinitely long straight wire having uniform negative linear charge density. Will the dipole be in equilibrium at these two positions? Justify your answer. (CBSE Sample Paper 2018-2019)

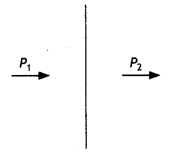
Answer:
The dipole will not be in equilibrium in any of the two positions.
The electric field due to an infinite straight charged wire is non-uniform (E ∝ 1/r).
Hence there will be a net non-zero force on the dipole in each case.

Question 9.
Two large parallel plane sheets have uniform charge densities +σ and -σ. Determine the electric field (i) between the sheets, and (ii) outside the sheets. (CBSE Delhi 2018)
Answer:
Let us consider two parallel planes charged conductors A and B carrying +ve and -ve charge density σ (charge per unit area). According to Gauss’ theorem, the electric intensity at P due to the charge on sheet A is

EA = \(\frac{\sigma}{2 \varepsilon_{0}}\) (From A and B)

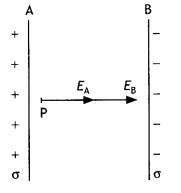
The electric field at P due to charge on sheet B is
E= \(\frac{\sigma}{2 \varepsilon_{0}}\) (From A to B)

The electric field at P is
E = EA + EB
= \(\frac{\sigma}{\varepsilon_{0}}\)

Question 10.
Define electric flux and write its SI unit. The electric field components in the figure shown are : E_x = αx, E_y = 0, E_z = 0 where α = 100N/cm. Calculate the charge within the cube, assuming a = 0.1 m. (CBSE Sample Paper 2019)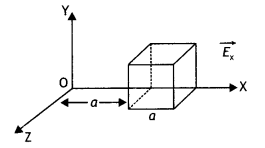
Or
An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0 × 10⁴ N/C (figure a)

(a) Calculate the time it takes to fall through this distance starting from rest.

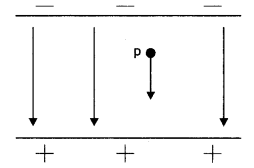
(b) If the direction of the field is reversed (figure b) keeping its magnitude unchanged, calculate the time taken by a proton to fall through this distance starting from rest. (CBSE Delhi 2018C)
Answer:
Electric Flux is the dot product of the electric field and area vector.
Φ = \(\oint \vec{E} \cdot \overrightarrow{d s}\)

SI Unit: Nm²/C or Vm

For a given case
Φ = Φ₁ – Φ₂ = [Ex(atx= 2a) – Ex (atx = a)]a²
= [α(2a)-α(a)]a² = αa³
= 10⁴ × (0.1 )³ = 10 Nm²/C
But
Φ = \(\frac{q}{\varepsilon_{0}}\)

∴ q = ε₀Φ = 8.854 × 10^-12 × 10 C = 8.54 pC
Or
We have
F = qE

Acceleration, a = \(\frac{q E}{m}\)

Also
s = \(\frac { 1 }{ 2 }\) at² [u = 0]
∴ t = \(\sqrt{\frac{2 s}{a}}\)

(i) For the electron
a = \(\frac { eE}{ m }\)

∴ t = \(\sqrt{\frac{2 s m}{e E}}\)

∴ t = \(\sqrt{\frac{3 \times 10^{-2} \times 9.1 \times 10^{-31}}{1.6 \times 10^{-19} \times 2.0 \times 10^{4}}}\) = 2.92 ns

(ii) for proton
t = \(\sqrt{\frac{2 \times 1.5 \times 10^{-2} \times 1.67 \times 10^{-27}}{1.6 \times 10^{-19} \times 2 \times 10^{4}}}\)
= -.125 μs

Question 11.
What will be the total flux through the faces of the cube (figure) with the side of length ‘a’ if a charge q is placed at
(a) A: a corner of the cube.
(b) B: mid-point of an edge of the cube.
(c) C: center of the face of the cube.
(d) D: mid-point of B and C. {NCERJ Exemplar)

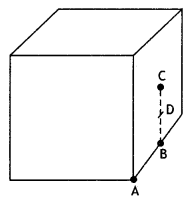
Answer:
(a) The charge wilt is shared by eight cubes if it has to be enclosed. Therefore the flux through the cube will be one-eighth of the total flux. Φ = q/8ε₀
(b) The charge will be shared by four cubes if it has to be enclosed. Therefore the flux through the cube will be one-fourth of the total flux. Φ = q/ 4ε₀
(c) The charge will be shared by two cubes if it has to be enclosed. Therefore the flux through the cube will be one-half of the total flux. Φ = q/ 2ε₀
(d) The charge will be shared by two cubes if it has to be enclosed. Therefore the flux through the cube will be one-half of the total flux. Φ = q/ 2ε₀

Question 12.
Two charges q and -3q are placed fixed on the x-axis separated by distance ‘d’. Where should a third charge 2q be placed such that it will not experience any force? (NCERT Exemplar)
Answer:
The situation is as shown.

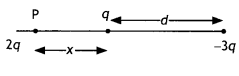
Let the charge 2q be placed at a distance ‘x’ from charge q. For the charge 2q to experience zero force we have
\(\frac{2 q^{2}}{4 \pi \varepsilon_{0} x^{2}}=\frac{6 q^{2}}{4 \pi \varepsilon_{0}(d+x)^{2}}\)
(d + x)² = 3x²

Solving for x we have
x = \(\frac{d}{2} \pm \frac{\sqrt{3} d}{2}\)
(-ve sign would be between q and -3q and hence is unacceptable.)

Therefore, we have
x = \(\frac{d}{2}+\frac{\sqrt{3} d}{2}=\frac{d}{2}(1+\sqrt{3})\) to the left of q.

Question 13.
(a) State Gauss’s law. Use it to deduce the expression for the electric field due to a uniformly charged thin spherical shell at points (i) inside and (ii) outside the shell. Plot a graph showing the variation of the electric field as a function of r > R and r < R. (r being the distance from the center of the shell) (CBSE Delhi 2011, Al 2013)
Answer:
Gauss’s law states that the net outward flux through any closed surface is equal to 1 /ε₀ times the charge enclosed by the closed surface.

Consider a thin spherical shell of radius R and center at O. Let σ be the uniform surface charge density (charge per unit surface area) and q be the total charge on it. The charge distribution is spherically symmetric. Three cases arise

Case 1: at a point outside the spherical shell
In order to find the electric field at a point P outside the shell let us consider a Gaussian surface in the form of a sphere of radius r (r >>R).

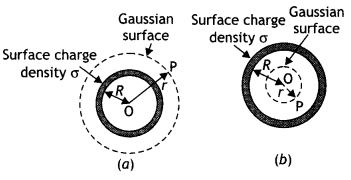
By symmetry, we find that the electric field acts radially outwards and has a normal component at alt points on the Gaussian sphere. Therefore by definition of electric flux we have

Φ = E × A, where A is the surface area of the Gaussian sphere therefore
Φ = E × 4πr² …(1)

But by Gauss’s law
Φ = \(\frac{Q}{\varepsilon_{0}}=\frac{\sigma A}{\varepsilon_{0}}=\frac{\sigma \times 4 \pi R^{2}}{\varepsilon_{0}}\) … (2)

from equations (1) and (2) it follows that
E × 4πr² = \(\frac{Q}{\varepsilon_{0}}\) Or E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{r^{2}}\)

E × 4πr² = \(\frac{\sigma \times 4 \pi R^{2}}{\varepsilon_{0}}\)

Ē = \(\frac{\sigma R^{2}}{\varepsilon_{0} r^{2}}\) … (3)

It follows that the electric field due to a spherical shell outside it is same as that due to a point charge. Therefore for points Lying outside the spherical shell the shell behaves as if the entire charge is concentrated at the centre.

Case 2: at a point inside the spherical shell
In this case, the Gaussian surface Lies inside the shell. Since no charge is enclosed In this surface therefore we have

E × 4πr²=q₀/ε₀ [∵ q=0]
Therefore E = 0

(b) Two identical metallic spheres A and B having charges +4Q. and -10 Q are kept a certain distance apart. A third identical uncharged sphere C is first placed in contact with sphere A and then with sphere B. Spheres A and B are then brought in contact and then separated. Find the charges on the spheres A and B. (CBSEAI 2011C)
Answer:
The initial charge on the sphere A = + 4 Q.
The initial charge on the sphere B = -10 Q.

Since all the three spheres are identical, i.e. they have the same capacity, therefore when uncharged sphere C is placed in contact with A, the total charge is equally shared between them.

Charge on C after contact with A
= \(\frac{0+4 Q}{2}\) = 2Q

Charge on A after contact with C is 2Q.
When sphere C carrying a charge 2Q is placed in contact with B, again charges are equally shared between C and B equally.

Charge on C after it is in contact with B
= \(\frac{2 Q-10 Q}{2}\) = -4Q

Now when sphere A with a charge of 2Q. is placed in contact with B, with charge -4Q.

Charge are again shared
∴ charge on A or B = \(\frac{2 Q-4 Q}{2}\) = -Q.

Question 14.
(a) Define electric dipole moment. Is it a scalar or a vector? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
Answer:
It is defined as the product of the magnitude of either of the two charges and the distance between them.
For derivation see sol. 9(a) of LA-II.

(b) Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero. (CBSE Al 2013)
Answer:
The diagram is as shown

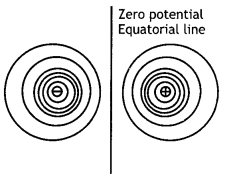
The zero potential points lie on the equatorial line.

Question 15.
(a) Using Gauss’s law obtain expressions for the electric field (i) inside, and (ii) outside a positively charged spherical shell.
(c) A Square plane sheet of side 10 cm is inclined at an angle of 30° with the direction of a uniform electric field of 200 NC“1. Calculate the electric flux passing through the sheet. (CBSE 2019C)
Answer:
(a) Spherical Shell
Consider a spherical shell of radius R. Let q be a charge on the shell. Let us find the electric field at a point P at a distance r from the center 0 of the spherical shell.

Case (i): When point P lies inside the spherical shell
From the point, P draws a Gaussian surface which will be a sphere of radius r.

From the Gauss’s Theorem,
\(\oint_{s} \vec{E} \cdot \vec{d} S=\frac{0}{\varepsilon_{0}}\) [∵ No charge exists inside the spherical shell]

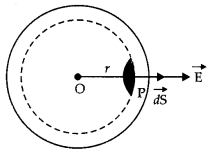
Or
E = 0
i. e. electric field inside the charged spherical shell is zero.

Case (ii): When point P is lying outside the shell (i.e. r > R)
From point P, draw a Gaussian surface which will be a spherical shell of radius r. Let dS be a small area element on the Gaussian surface P.


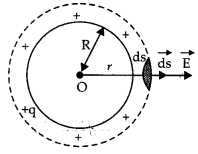
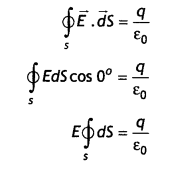
Or

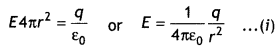
i. e. the electric field outside the spherical shell behaves as if the whole charge is concentrated at the center of the spherical shell.

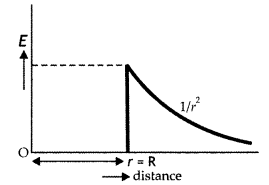
(b) Show graphically variation of the electric field as a function of the distance r from the center of the sphere.
Answer:
Variation of electric field E with distance
The given figure shows the variation of an electric field with distance from the center of the charged spherical shell.

(c) Here E = 200 N/C, S = 0.1 × 0.1 = 0.01 m²
And θ = 90° – 30° = 60°

The electric flux linked with the square sheet
Φ = E S cos 60°
= 200 × 0.01 × \(\frac { 1 }{ 2 }\) = 1.0 Nm² C^-1

Question 16.
A charge is distributed uniformly over a ring of radius ‘a’. Obtain an expression for the electric intensity E at a point on the axis of the ring. Hence show that for points at a large distance from the ring, it behaves like a point charge. (CBSE Delhi 2016)
Answer:
Consider a uniformly charged ring of radius ‘a’. Let the total charge on the ring be Q, Let us find the electric field on the axis of the ring at point P distance x from the center of the ring. Consider a segment of charge dQ as shown in the figure.

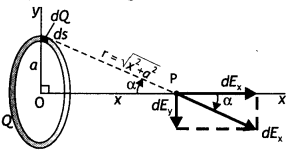
The magnitude of etectñc field at P due to the segment is
dE=k\(\frac{d Q}{r^{2}}\) …(1)

This field can be resolved into its components: x component dE_x = dE cos α an along the axis of the ring and y component dE perpendicular to the axis. Since these perpendicular components, due to alt the charge segments, are equal and opposite, therefore they cancel out each other. From the diagram we have r = \(\sqrt{x^{2}+a^{2}}\) and cos α = x/r, therefore we have
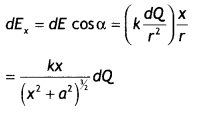…(2)

In this case, all the segments of the ring give the same contribution to the field at P since they are all equidistant from this point. Thus we can easily sum over all segments to get the total electric field at point P

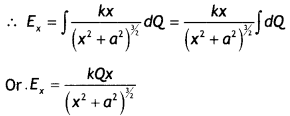
If the point of observation is far away, i.e. x >> a, then E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{x^{2}}\). This is the same as that for a point charge. Thus at far-off axial points, a charged ring behaves as if a point charge is situated at the center of the ring.

Question 17.
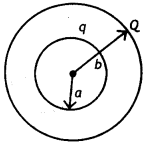
Two thin concentric and coplanar spherical shells, of radii ‘a’ and ‘b’ (b > a), carry charges, q, and Q respectively. Find the magnitude of the electric field, at a point distant x, from their common center for
(i) O < x < a
(ii) a ≤ x < b
(iii) b ≤ x < ∞ (CBSE Delhi 2016C)
Answer:
The diagram is as shown.

(i) For 0 < x < a
Point Lies inside both the spherical shells.

∴ charge enclosed = 0
Hence, E(x) = 0

(ii) For a < x < b
Point is outside the spherical shell of radius ‘a’ but inside the spherical Shell of radius ‘b’.
Therefore

(iii) For b ≤ x< ∞
The point is outside of both the spherical shells. The total effect we charge at the center equals (Q + q).

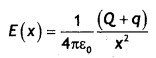
Question 18.
(a) Define electric flux. Is It a scalar or a vector quantity?

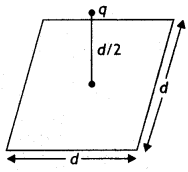
A point charge q is at a distance of d/2 directly above the center of a square of side d, as shown In the figure. Us. Gauss’s law to obtain the expression for the electric flux through the square.
Answer:
The electric flux through a given surface is defined as the dot product of the electric field and area vector over that surface. It is a scalar quantity.

Constructing a cube of side ‘d’ so that charge ‘q’ gets placed within this cube (Gaussian surface)
According to Gauss’s law the electric flux
Φ = \(\frac{q}{\varepsilon_{0}}\)

This is the total flux through all the six faces of the cube.

Hence electric flux through the square (one face of the cube)
Φ = \(\frac{1}{6} \frac{q}{\varepsilon_{0}}\)

(b) If the point charge is now moved to a distance ‘d’ from the center of the square and the side of the square is doubled, explain how the electric flux will be affected. (CBSE Al, Delhi 2018)
Answer:
If the charge is moved to a distance ‘d’ and the side of the square is doubled the cube will be constructed to have a side 2d but the total charge enclosed in it will remain the same. Hence the total flux through the cube and therefore the flux through the square will remain the same as before.

Question 19.
(a) Draw a graph to show the variation of E with perpendicular distance r from the line of charge.
Answer:
The required graph is

(b) Find the work done in bringing a charge q from perpendicular distance r₁ to r₂ (r₂ > r₁). (CBSEAI, Delhi 2018)
Answer:
Work done in moving the charge “q”. through a smaLL displacement ‘dr’

dW = \(\vec{F}\) . \(\vec{dr}\) =q\(\vec{E}\) .\(\vec{dr}\)
dW = qE dr cos 0 = qEdr
dW= q x \(\frac{\lambda}{2 \pi \varepsilon_{0} r}\) dr

Hence work done in moving the charge from r₁ to r₂ (r₂ > r₁)

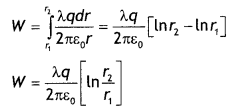
Question 20.
Derive an expression for the torque acting on an electric dipole of dipole moment \(\vec{p}\) placed in a uniform electric field \(\vec{E}\). Write the direction along which the torque acts.
OR
Derive an expression for the electric field at a point on the axis of an electric dipole of dipole moment \(\vec{p}\). Also, write its expression when the distance r >> a the length ‘a’ of the dipole. (CBSEAI 2019)
Answer:
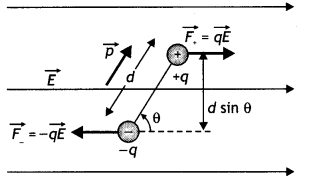
Consider an electric dipole consisting of charges -q and +q and dipole length d is placed in a uniform electric field E as shown in the figure.

Let the dipole moment makes an angle θ with the direction of the electric field. The two charges experience force qE each.

These forces are equal, parallel, and opposite. Therefore, the net force acting on the dipole is
F_n = qE – qE = 0

Thus the net force acting on the dipole is zero.

These two forces constitute a couple. This applies a torque on the dipole given by
τ = either force × arm of the couple
τ = qE × d sin θ, where d sin θ is the arm of the couple.
τ = q d Esin θ, where p = qd, dipole moment
τ = pE sin θ.

Consider an electric dipole consisting of -q and +q charges separated by a distance 2a as shown in the figure. Let P be the point of observation on the axial Line where the electric field has to be found. Let it be at a distance r from the center O of the dipole. Let us suppose that the dipole is placed in a vacuum.

Let E and E_B be the electric fields at point P due to the charges at A and B respectively. Therefore,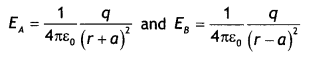

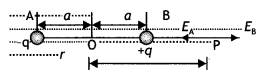
The two fields at P are in opposite directions. Thus the resultant electric field at P is given by
E = \(\sqrt{E_{A}^{2}+E_{B}^{2}-2 E_{A} E_{B} \cos \theta}=\sqrt{\left(E_{B}-E_{A}\right)^{2}}\) = E_B – E_A

since θ = 180⁰ Therefore, the resultant electric field is

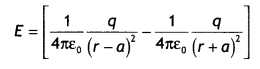
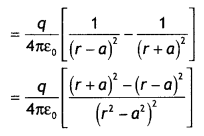
Solving we have

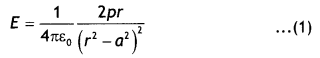
where p = q 2a.
If the dipole is short then r >> a, therefore, ‘a’ is neglected as compared to r, hence

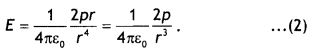
This field is in the direction of the dipole moment.

Question 21.
(a) Derive the expression for the electric field at a point on the equatorial line of an electric dipole. (CBSE 2019C)
Answer:
Consider an electric dipole consisting of charges -q and +q separated by a distance 2a as shown in the figure. Let the point of observation P lie on the. right bisector of the dipole AB at a distance r from its midpoint 0. Let E_A and E_B be the electric field intensities at point P due to charges at A and B, respectively.

The two electric fields have magnitudes

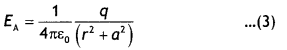
in the direction of AP

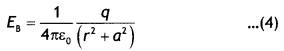
in the direction of PB.

The two fields are equal in magnitude but have different directions. Resolving the two fields E_A and E_B into their rectangular components, i.e. perpendicular to and parallel to AB. The components perpendicular to AB, i.e E_A sinG and E_B sinG being equal and opposite cancel out each other while the components parallel to AB, i.e. E_A cos θ and E_B cos θ being in the same direction add up as shown in the figure. Hence the resultant electric field at point P is given by

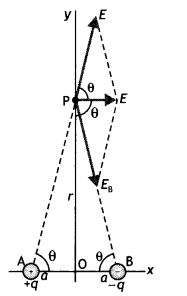
E = E_Acosθ + E_Bcosθ

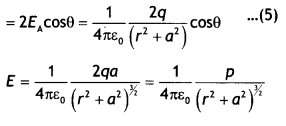
∵ cos θ = \(\frac{a}{\left(r^{2}+a^{2}\right)^{1 / 2}}\) and q 2a = p

For a short dipole r²,>>a² therefore
E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{p}{r^{3}}\)

(b) Discuss the orientation of the dipole in (a) stable, (b) unstable equilibrium in a uniform electric field. (CBSE Delhi 2017)
Answer:
For stable equilibrium \(\vec{P}\) is along \(\vec{E}\)
θ = 0°, τ = PE sin 0°, Torque alligns the dipole in the direction of field

For unstable equilibrium \(\vec{P}\) is antiparallel to \(\vec{E}\)
∵ θ = 180°, τ = PE sin 180° = 0, Torque alligns the dipole in a direction opposite to \(\vec{E}\).

Question 22.
(a) An electric dipole of dipole moment \(\vec{p}\) consists of point charges +q and -q separated by a distance 2a apart. Deduce the expression for the electric field due to the dipole at a distance x from the center of the dipole on its axial line in terms of the dipole moment. Hence show that in

the limit r >> a, \(\vec{E}\) → \(\frac{2 \vec{p}}{4 \pi \varepsilon_{0} r^{3}}\)
Answer:

Consider an electric dipole consisting of charges -q and +q and dipole length d is placed in a uniform electric field E as shown in the figure.

Let the dipole moment makes an angle θ with the direction of the electric field. The two charges experience force qE each.

These forces are equal, parallel, and opposite. Therefore, the net force acting on the dipole is
F_n = qE – qE = 0

Thus the net force acting on the dipole is zero.

These two forces constitute a couple. This applies a torque on the dipole given by
τ = either force × arm of the couple
τ = qE × d sin θ, where d sin θ is the arm of the couple.
τ = q d Esin θ, where p = qd, dipole moment
τ = pE sin θ.

Consider an electric dipole consisting of -q and +q charges separated by a distance 2a as shown in the figure. Let P be the point of observation on the axial Line where the electric field has to be found. Let it be at a distance r from the center O of the dipole. Let us suppose that the dipole is placed in a vacuum.

Let E and EB be the electric fields at point P due to the charges at A and B respectively. Therefore,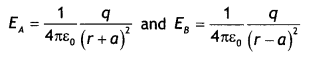

The two fields at P are in opposite directions. Thus the resultant electric field at P is given by
E = \(\sqrt{E_{A}^{2}+E_{B}^{2}-2 E_{A} E_{B} \cos \theta}=\sqrt{\left(E_{B}-E_{A}\right)^{2}}\) = E_B – E_A

since θ = 1800 Therefore, the resultant electric field is

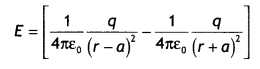
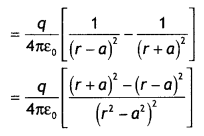
Solving we have

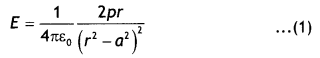
where p = q 2a.
If the dipole is short then r >> a, therefore, ‘a’ is neglected as compared to r, hence

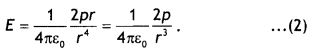
This field is in the direction of the dipole moment.

(b) Given the electric field in the region E = 2xî, find the net electric flux through the cube and the charge enclosed by it. (CBSE Delhi 2015)

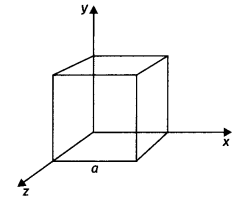
Answer:
Since the electric field has only an x component, for faces perpendicular to the x-direction, the angle between E and ΔS is ± π/2.

Therefore, the flux Φ = E.ΔS is separately zero for each face of the cube except the two faces along the X-axis.

Now the magnitude of the electric field at the left face is
E_L= 0 (x = 0 at the left face)

The magnitude of the electric field at the right face is
E_R = 2x = 2a (x = a at the right face)

The corresponding fluxes are
Φ_L = E_L.ΔS = ΔS (\(\vec{E}_{L} \cdot \hat{n}_{\mathrm{L}}\)) = E_LΔS COS θ
= – E_L ΔS = 0, since θ =180°

Φ_R = E_R.ΔS = E_RΔS cos θ = E ΔS = (2a)a², since θ = 0°

Net flux through the cube
Φ = -Φ_R + Φ_L = 2a³ -0 = 2a³

We can use Gauss’s law to find the total charge q inside the cube.
We have Φ = q/ε₀ or q = Φε₀. Therefore, q = 2a³ × 8.854 × 10^-12C

Question 23.
(a) Derive an expression for the electric field at any point on the equatorial line of an electric dipole.
Answer:
Consider an electric dipole consisting of charges -q and +q separated by a distance 2a as shown in the figure. Let the point of observation P lie on the. right bisector of the dipole AB at a distance r from its midpoint 0. Let EA and EB be the electric field intensities at point P due to charges at A and B, respectively.

The two electric fields have magnitudes

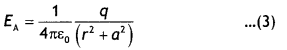
in the direction of AP

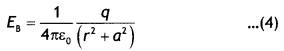
in the direction of PB.

The two fields are equal in magnitude but have different directions. Resolving the two fields E_A and E_B into their rectangular components, i.e. perpendicular to and parallel to AB. The components perpendicular to AB, i.e E_A sinG and E_B sinG being equal and opposite cancel out each other while the components parallel to AB, i.e. E_A COS θ and E_B cos θ being in the same direction add up as shown in the figure. Hence the resultant electric field at point P is given by

E = E_A cos θ + E_B cos θ

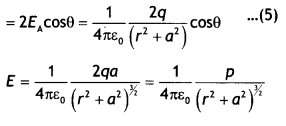
∵ cos θ = \(\frac{a}{\left(r^{2}+a^{2}\right)^{1 / 2}}\) and q 2a = p

For a short dipole r²,>>a² therefore
E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{p}{r^{3}}\)

(b) Two identical point charges, q each, are kept 2 m apart in the air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q. (CBSE Delhi 2019)
Answer:
The third charge Q. wilt is in equilibrium if it experiences zero net force. Let it be placed at a distance x meter from the charge q.

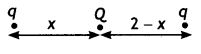
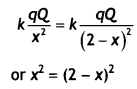
Solving for x, we have x= 1 m

For the equilibrium of charges “q”, the nature of charge Q must be opposite to the nature of charge q and should be placed at the center of two charges.

Question 24.
(a) Define electric flux. Write its S.I. unit.
Answer:
It is defined as the total number of electric field lines crossing a given area. The electric flux can be found by multiplying the component of the electric field in the direction of the area vector (or perpendicular to the area) with the area of the closed surface. It is measured in Nm²C-^-1.

(b) A small metal sphere carrying charge +Q is located at the center of a spherical cavity inside a large uncharged metallic spherical shell as shown in the figure. Use Gauss’s law to find the expressions for the electric field at points P₁ and P₂.

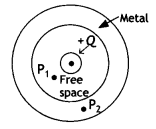
Answer:
For point P, using Gauss law we have

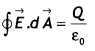
Since E and dA are in the same direction therefore we have E = \(\frac{Q}{\varepsilon_{0} A}\)

Point P₂ lies inside the metal, therefore the Gaussian surface drawn at P₂ does not include a charge, hence the electric field at P₂ is zero.

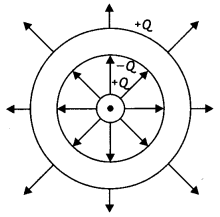
(c) Draw the pattern of electric field lines in this arrangement. (CBSEAI 2012C)
Answer:
The electric field lines are as shown.

Question 25.
(a) Deduce the expression for the torque acting on a dipole of dipole moment \(\vec{P}\) in the presence of a uniform electric field \(\vec{E}\)
Answer:

Consider an electric dipole consisting of charges -q and +q and dipole length d is placed in a uniform electric field E as shown in the figure.

Let the dipole moment makes an angle θ with the direction of the electric field. The two charges experience force qE each.

These forces are equal, parallel, and opposite. Therefore, the net force acting on the dipole is
F_n = qE – qE = 0

Thus the net force acting on the dipole is zero.

These two forces constitute a couple. This applies a torque on the dipole given by
τ = either force × arm of the couple
τ = qE × d sin θ, where d sin θ is the arm of the couple.
τ = q d Esin θ, where p = qd, dipole moment
τ = pE sin θ.

Consider an electric dipole consisting of -q and +q charges separated by a distance 2a as shown in the figure. Let P be the point of observation on the axial Line where the electric field has to be found. Let it be at a distance r from the center O of the dipole. Let us suppose that the dipole is placed in a vacuum.

Let E and EB be the electric fields at point P due to the charges at A and B respectively. Therefore,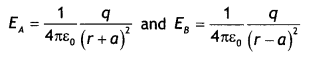

The two fields at P are in opposite directions. Thus the resultant electric field at P is given by
E = \(\sqrt{E_{A}^{2}+E_{B}^{2}-2 E_{A} E_{B} \cos \theta}=\sqrt{\left(E_{B}-E_{A}\right)^{2}}\) = E_B – E_A

since θ = 180° Therefore, the resultant electric field is

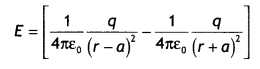
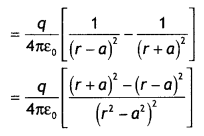
Solving we have

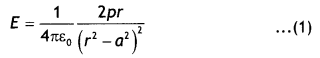
where p = q 2a.
If the dipole is short then r >> a, therefore, ‘a’ is neglected as compared to r, hence

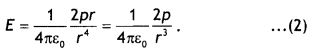
This field is in the direction of the dipole moment.

(b) Consider two hollow concentric spheres S₁ and S₂ and enclosing charges 2Q and 4Q. respectively as shown in the figure, (i) Find out the ratio of the electric flux through them, (ii) How will the electric flux through the sphere S₁ change if a medium of dielectric constant ‘er’ is introduced in the space inside S1 in place of air? Deduce the necessary expression. (CBSE Al 2014)

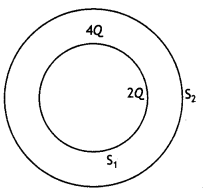
Answer:
Φ₁ = \(\frac{2 Q}{\varepsilon_{0}}\) and Φ2 = \(\frac{2 Q+4 Q}{\varepsilon_{0}}=\frac{6 Q}{\varepsilon_{0}}\)

Hence ratio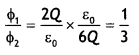

When a dielectric of dielectric constant εr is introduced then we have
Φ₁ = \(\frac{2 Q}{\varepsilon}=\frac{2 Q}{\varepsilon_{r} \varepsilon_{0}}\)

Question 26.
(a) Use Gauss’s theorem to find the electric field due to a uniformly charged infinitely large plane thin sheet with surface charge density σ.
Answer:
It states, “The net electric flux through any Gaussian surface is equal to \(\frac{1}{\varepsilon_{0}}\) times the net electric charge enclosed by the surface.

Mathematically, Φ =\( \phi \vec{E} \cdot d \vec{A}=\frac{q_{i n}}{\varepsilon_{0}}\)

Consider an infinite plane sheet of charge. Let a be the uniform surface charge density, i.e. the charge per unit surface area. From symmetry, we find that the electric field must be perpendicular to the plane of the sheet and that the direction of E on one side of the plane must be opposite to its direction on the other side as shown in the figure below. In such a case let us choose a Gaussian surface in the form of a cylinder with its axis perpendicular to the sheet of charge, with ends of area A.

The charged sheet passes through the middle of the cylinder’s length so that the cylinder’s ends are equidistant from the sheet. The electric field has a normal component at each end of the cylinder and no normal component along the curved surface of the cylinder. As a result, the electric flux is linked with only the ends and not the curved surface.

Therefore by the definition of eLectric flux, the flux Linked with the Gaussian surface is given by
Φ = \(\oint_{A} \vec{E} \cdot \vec{\Delta} A\)

Φ = E_A + E_A = 2E_A … (1)

But by Gauss’s Law

Φ = \(\frac{q}{\varepsilon_{0}}=\frac{\sigma A}{\varepsilon_{0}}\) [∵ q = σA] … (2)

From equations (1) and (2), we have

2E_A = \(\frac{\sigma A}{\varepsilon_{0}}\) … (3)

E = \(\frac{\sigma}{2 \varepsilon_{0}}\) …. (4)

This gives the electric field due to an infinite plane sheet of charge which is independent of the distance from the sheet.

(b) An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the expression for the amount of work done in bringing a point charge q from infinity to a point, distant r, in front of the charged plane sheet. (CBSE Al 2017)
Answer:
Work done

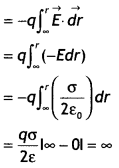
Numerical Problems:

Formulae for solving numerical problems

• q = ±ne
• F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)
• Fmed = \(\frac{1}{4 \pi \varepsilon_{0} K} \frac{q_{1} q_{2}}{r^{2}}\) where K is dielectric constant.
• 
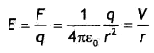
• E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{2 p}{r^{3}}\) for an electric dipole on its axial line.
• E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{p}{r^{3}}\) for an electric dipole on its equitorial line.
• Torque on an electric dipole in a uniform electric field, τ = PE sin θ.
• U = -pE cos θ, the potential energy of an electric dipole.
• Φ = \(\oint \vec{E} \cdot d \vec{A}=\frac{q_{\text {in }}}{\varepsilon_{0}}\)
• E = \(\frac{\sigma}{2 \varepsilon_{0}}\) , electric field due to an infinite plane sheet of charge.

Question 1.
An electric dipole of length 2 cm is placed with its axis making an angle of 60° to a uniform electric field of 105 NC^-1. If it experiences a torque of 8\(\sqrt{3}\) Nm, calculate the (i) magnitude of the charge on the dipole and (ii) potential energy of the dipole.
Answer:
(i) Using
q = τ / L E sin Φ

we have
q = 8N\(\sqrt{3}\) × 2 / 2 × 10^-2 × 10⁵ × \(\sqrt{3}\) = 8 × 10^-3 C

(ii) Using U = -pE cos θ, we have
U = – 8 × 10^-3 × 0.02 × 10⁵ × 0.5 = – 8 J

Question 2.
A charge of 17.7 × 10^-4 C is distributed uniformly over a large sheet of area 200 m². Calculate the electric field intensity at a distance of 20 cm from it in the air.
Answer:
Given q = 17.7 × 10^-4C, A = 200 m², r = 20cm = 0.2 m

Using the relation

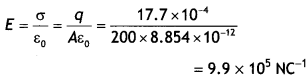
Question 3.
Two fixed point charges +4e and +e units are separated by a distance ‘a’. Where should the third point charge be placed for it to be in equilibrium?
Answer:
The third charge will be in equilibrium if it experiences zero net force. Let it be placed at a distance x from the charge 4e.

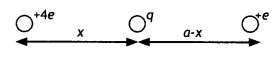
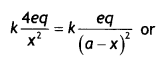
4(a – x)² = x² solving for x we have
2 (a – x) = x or x = a/3

Question 4.
An electric field along the x-axis is given by \(\vec{E}\) = 100 îN/C for x > 0 and \(\vec{E}\) = -100 îN/C for x < 0. A right circular cylinder of length 20 cm and radius 5 cm lies parallel to the x-axis with its centre at the origin and one face at x = +10 cm, the other face at x = -10 cm. Calculate the net outward flux through the cylinder. (CBSE 2019C)

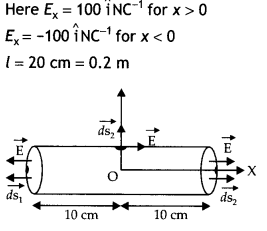
r = 5 cm = 0.05 m
Φ = ?

Net outward flux through the cylinder
Φ = Φ₁ + Φ₂ + Φ₃
= \(\vec{E} \cdot \overrightarrow{d s}_{1}+\vec{E} \cdot \overrightarrow{d s}_{2}+\vec{E} \cdot \overrightarrow{d s}_{3}\)

= Eds₁ cos 180° + Eds₂ cos 90° + Eds3 cos 0°
= – Eds₁ + Eds₂ (0) + Eds cos 0°
= – (-100) ds + 100 ds
= (100 +100) ds
= 200 × πr² = 200 × 3.14 × (0.05)²
= 1.57 Nm² C^-1

Question 5.
A hollow cylindrical box of length 1m and area of cross-section 25 cm² is placed in a three-dimensional coordinate system as shown in the figure. The electric field
in the region is given by \(\vec{E}\) = 50x î, where E is in NC^-1 and x is in meters. Find

(i) Net flux through the cylinder.
Answer:
We can see from the figure that on the left face E and dS are antiparallel. Therefore, the flux is
ΦL = \(\vec{E}\).\(\vec{dS}\) = E dS cos 180°
= -50 × 1 × 25 × 10^-4 = -0.125 N m² C^-1

On the right face, E and dS are parallel and therefore
ΦR = \(\vec{E}\).\(\vec{ds}\) = EdS cos 0°
= 50 × 2 × 25 × 10^-4 = 0.250 N m² C^-1

Therefore net flux is – 0.125 + 0.250 = + 0.125 N m² C^-1

(ii) Charge enclosed by the cylinder. (CBSE Delhi 2013)

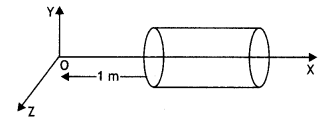
Answer:
q = Φε₀ = 0.125 × 8.854 × 10^-12 = 1.1 × 10^-12C

Question 6.
(i) Define electric flux. Write its SI units,
Answer:
(i) It is defined as the number of electric field lines crossing a unit area perpendicular to the given area. It is measured in N m² C^-1

(ii) Consider a uniform electric field \(\vec{E}\) = 5 × 10³î NC^-1. Calculate the flux of this field through a square surface of area 12 cm² when
(a) its plane is parallel to the Y – Z plane, and
(b) the normal to its plane makes a 60° angle with the x-axis. (CBSE Delhi 2013C)
Answer:
Given \(\vec{E}\) = 5 × 10³î N C^-1, A = 12 cm² = 12 × 10^-4 m²

(a) Here \(\vec{E}\) = 5 × 103î N C^-1
Area of square = 12 × 10^-4 m²

The plane of surface area being parallel to YZ plane, hence
A = 12 × 10^-4 î m²

Electric flux of the field
Φ = \(\vec{E}\) \(\vec{A}\) = (5 × 10³ î). (12 × 10^-4î) = 6 N C^-1 m²
(b) When normal to the plane of surface area makes an angle of 60° with the X-axis, the flux is given by
Φ = EA cos 0 = 5 × 10³ × 12 × 10^-4 × 0.5
= 3 NC^-1 m²