Wave Optics Class 12 Important Extra Questions Physics Chapter 10

Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 10 Wave Optics. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.

Class 12 Physics Chapter 10 Important Extra Questions Wave Optics

Wave Optics Important Extra Questions Very Short Answer Type

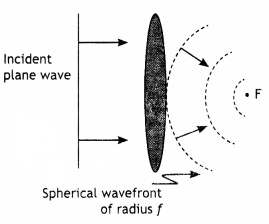
Question 1.
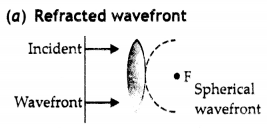
Sketch the refracted wavefront emerging from convex tens, If a plane wavefront is an incident normally on it.
Answer:
The figure is as shown.

Question 2.
How would you explain the propagation of light on the basis of Huygen’s wave theory?
Answer:
To explain the propagation of light we have to draw a wavefront at a later instant when a wavefront at an earlier instant is known. This can be drawn by the use of Huygen’s principle.

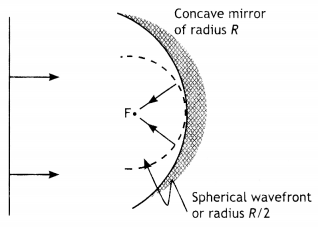
Question 3.
Draw the shape of the reflected wavefront when a plane wavefront is an incident on a concave mirror.
Answer:
The reflected wavefront is as shown.

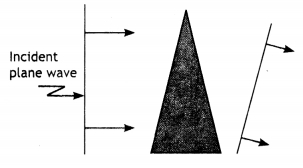
Question 4.
Draw the shape of the refracted wavefront when a plane wavefront is an incident on a prism.
Answer:
The shape of the wavefront is as shown.

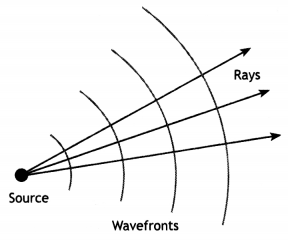
Question 5.
Draw the type of wavefront that corresponds to a beam of light diverging from a point source.
Answer:
The wavefront formed by the light coming from a very far off source is a plane and for a beam of light diverging from a point, a wavefront is a number of concentric circles.

Question 6.
Draw the type of wavefront that corresponds to a beam of light coming from a very far off source.
Answer:
The wavefront is as shown.

Question 7.
Name two phenomena that establish the wave nature of light.
Answer:
Interference and diffraction of light.

Question 8.
State the conditions which must be satisfied for two light sources to be coherent.
Answer:
(a) Two sources must emit light of the same wavelength (or frequency).
(b) The two light sources must be either in-phase or have a constant phase difference.

Question 9.
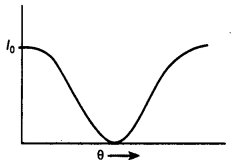
Draw an intensity distribution graph for diffraction due to a single-slit.
Answer:
The intensity distribution for a single-slit diffraction pattern is as shown.

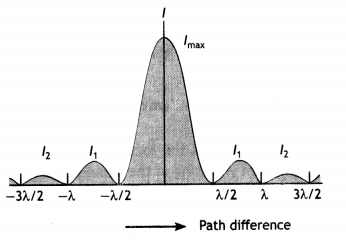
Question 10.
Name one device for producing plane polarised light. Draw the graph showing the variation of intensity of polarised light transmitted by an analyser.
Answer:
Nicol prism can be used to produce plane polarised light. The graph is as shown.

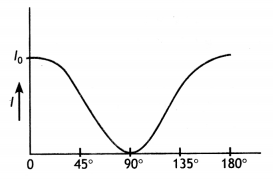
Question 11.
State Huygens’ principle of diffraction of light. (CBSE AI 2011C)
Answer:
Huygens principle states that
(a) Each point on a wavefront is a source of secondary waves which travel out with the same velocity as the original waves.
(b) The new wavefront is given by the forward locus of the secondary wavelets.

Question 12.
In what way is a plane polarised tight different from an unpolarised light? (CBSE AI 2012C)
Answer:
Plane polarized light vibrates 1n only one plane.

Question 13.
Which of the following waves can be polarised: (i) Heatwaves (ii) Sound waves? Give a reason to support your answer. (CBSE Delhi 2013)
Answer:
Heatwaves are transverse In nature.

Question 14.
Define the term ‘wavefront’. (CBSE AI 2014C)
Answer:
It Is defined as the locus of all points In a medium vibrating in the same phase.

Question 15.
Define the term ‘coherent sources’ which are required to produce interference pattern in Young’s double-slit experiment. (CBSE Delhi 2014C)
Answer:
Two sources that are In phase or have a constant phase difference are called coherent sources.

Question 16.
What change would you expect if the whole of Young’s double-slit apparatus were dipped into the water?
Answer:
The wavelength λ, of light In water, is less than that in air. Since the fringe width β is directly proportional to the wavelength of light, therefore, the fringe width will decrease.

Question 17.
When light travels from a rarer to a denser medium, it loses some speed. Does the reduction in speed Imply a reduction in the energy carried by the light wave?
Answer:
No, the energy carried by a wave depends upon the amplitude of the wave and not on Its speed of propagation.

Question 18.
If one of the slits say S₁, is covered then what changes occur in the Intensity of light at the centre of the screen?
Answer:
The intensity 1s decreased four times because l ∝ 4a² where a is the amplitude of each wave.

Question 19.
How does the angular separation between fringes in a single-slit diffraction experiment change when the distance of separation between the slit and screen is doubled? (CBSE AI 2012)
Answer:
No change.

Question 20.
What is the effect on the interference fringes in Young’s double-slit experiment If the separation between the screen and slits Is Increased?
Answer:
The fringe width Increases.

Question 21.
How does the Intensity of the central maximum change If the width of the slit Is halved in a single-slit diffraction experiment?
Answer:
The width of the central maxima is doubled and the intensity is reduced to one-fourth of Its original value.

Question 22.
The polarising angle of a medium Is 60°, what is the refractive index of the medium? (CBSE Delhi 2019)
Answer:
Using the expression
μ = tan i_p = tan 60° = 1.732.

Question 23.
In the wave picture of light intensity of light is determined by the square of the amplitude of the wave. What determines the intensity of light in the photon picture of light?
Answer:
For a given frequency intensity of light in the photon, the picture is determined by the number of photons crossing a unit area per unit time.

Question 24.
How does the Intensity of the central maximum change if the width of the slit is halved in the single-slit diffraction experiment?
Answer:
The width of the central maximum is doubled and the intensity is reduced to one-fourth of its original value.

Question 25.
What would happen If the path difference between the interfering beams that is S₂P – S₁P became very large?
Answer:
If the path difference becomes very large it may exceed the coherent length. Thus the coherence of the waves reaching P is lost and no interference takes place.

Question 26.
In Young’s double-slit experiment, what would happen to the intensity of the maxima and the minima if the size of the hole illuminating the two coherent holes were gradually Increased?
Answer:
The fringe width will decrease and finally, there will be general illumination on the screen.

Question 27.
What is the Brewster angle for air to glass transition? (Refractive index of glass =1.5.) (NCERT)
Answer:
Given μ = 1.5, i_P = ?
Using the relation μ = tan i_P we have
l_p = tan^-1 (1.5) = 56.3°

Question 28.
Is Huygen’s principle valid for longitudinal sound waves? (NCERT Exemplar)
Answer:
Yes

Question 29.
Consider a point at the focal point of a convergent lens. Another convergent lens of the short focal length is placed on the other side. What is the nature of the wavefronts emerging from the final image? (NCERT Exemplar)
Answer:
Spherical.

Question 30.
What is the shape of the wavefront on earth for sunlight? (NCERTExemplar)
Answer:
Spherical with a huge radius as compared to the earth’s radius so that it is almost a plane.

Question 31.
Draw a graph showing the intensity distribution of fringes due to diffraction at a single-slit. (CBSE 2018C)
Answer:

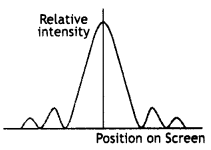
Wave Optics Important Extra Questions Short Answer Type

Question 1.
How can one distinguish between an unpolarised and linearly polarised light beam using polaroid? (CBSE Delhi 2019)
Answer:
The two lights will be allowed to pass through a polariser. When the polarizer is rotated in the path of these two light beams, the intensity of light remains the same in all the orientations of the polariser, then the light is unpolarised. But if the intensity of light varies from maximum to minimum then the light beam is a polarised light beam.

Question 2.
What is meant by plane polarised light? What type of waves shows the property of polarisation? Describe a method of producing a beam of plane polarised light?
Answer:

1. The light that has its vibrations restricted in only one plane is called plane polarised light.
2. Transverse waves show the phenomenon of polarization.
3. Light is allowed to pass through a polaroid. The polaroid absorbs those vibrations which are not parallel to its axis and allows only those vibrations to pass which are parallel to its axis.

Question 3.
Write the Important characteristic features by which the Interference can be distinguished from the observed diffraction pattern. (CBSE AI 2015)
Answer:
(a) In the interference pattern the bright fringes are of the same width, whereas in the diffraction pattern they are not of the same width.
(b) In interference all bright fringes are equally bright while in diffraction they are not equally bright.

Question 4.
State Brewster’s law. The value of Brewster’s angle for the transparent medium is different for the light of different colours. Give reason. (CBSE Delhi 2016)
Answer:
When the reflected ray and the refracted ray are perpendicular then μ = tani_p where i_p is the polarising angle or Brewster angle.

Brewster’s angle depends upon the refractive index of the two media in contact. The refractive index in turn depends upon the wavelength of light used (different colours) hence Brewster’s angle is different for different colours.

Question 5.
Discuss the intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids.
Answer:
Let l_o be the intensity of polarised light after passing through the first polarizer P₁. Then the intensity of light after passing through the second polarizer P2 will be l = l_ocos 2θ, where θ is the angle between pass axes of P₁ and P₂. Since P₁ and P₃ are crossed the angle between the pass axes of P₂ and P₃ will be (π/2 – θ). Hence the intensity of light emerging from P₃ will be
l = l_o cos² θ cos² (90° – θ) = l_o cos² θ sin² θ = (l_o /4)sin² 2θ

Therefore, the transmitted intensity will be maximum when θ = π/4

Question 6.
Is energy conserved in interference? Explain.
Answer:
Yes, energy is conserved in interference. Energy from the dark fringes is accumulated in the bright fringes. If we take
l = 4a²cos²\(\frac{\phi}{2}\), then intensity at bright points is l_max = 4a² and intensity at the minima l_min = 0. Hence average intensity in the pattern of the fringes produced due to interference is given by
Ī = \(\frac{I_{\max }+I_{\min }}{2}=\frac{4 a^{2}+0}{2}\) = 2a²

But if there is no interference then total intensity at every point on the screen will be l = a² + a² = 2a², which is the same as the average intensity in the interference pattern.

Question 7.
An incident beam of light of intensity lo is made to fall on a polaroid A. Another polaroid B is so oriented with respect to A that there is no light emerging out of B. A third polaroid C is now introduced midway between A and B and is so oriented that its axis bisects the angle between the axes of A and B. What is the intensity of light now between (i) A and C (ii) C and B? Give reasons for your answers.
Answer:
Polaroids A and B are oriented at an angle of 90°, so no light is emerging out of B. On placing polaroid C between A and B such that its axis bisects the angle between axes of A and B, then the angle between axes of polaroids A and B is 45° and that of C and B also 45°.
(a) Intensity of light on passing through Polaroid A or between A and C is l₁ = \(\frac{l_{0}}{2}\)
(b) On passing through polaroid C, intensity of light between C and B becomes
l₂ = l₁ cos² θ = \(\frac{l_{0}}{2}\) × cos² 45° = \(\frac{l_{0}}{4}\)

Question 8.
One of the slits of Young’s double-slit experiment is covered with a semi¬transparent paper so that it transmits lesser light. What will be the effect on the interference pattern?
Answer:
There will be an interference pattern whose fringe width is the same as that of the original. But there will be a decrease in the contrast between the maxima and the minima, i.e. the maxima will become less bright and the minima will become brighter.

Question 9.
Light from a sodium lamp is passed through two polaroid sheets P₁ and P₂ kept one after the other. Keeping P₁, fixed, P₂ is rotated so that its ‘pass axis can be at different angles, θ, with respect to the pass-axis of P₁.
An experimentalist records the following data for the intensity of light coming out of P₂ as a function of the angle θ.

I = Intensity of beam falling on P₁
(a) One of these observations is not in agreement with the expected theoretical variation of I, identify this observation and write the correct expression.
(b) Define the Brewster angle and write the expression for It in terms of the refractive index of the medium.
Answer:
(a) The observation \(\frac{1}{\sqrt{2}}\) is not correct. It should be 1/2.
(b) It is the angle of incidence at which the refracted and the reflected rays are perpendicular to each other. It is related to the refractive index as tan i_p = μ

Question 10.
How will the interference pattern in Young’s double-slit experiment get affected, when
(a) distance between the slits S₁, and S₂ reduced and
(b) the entire set-up is immersed in water? Justify your answer in each case. (CBSE Delhi 2011C)
Answer:
We know that fringe width β of the dark or bright fringes is given by β = \(\frac{D \lambda}{d}\) where d is the distance between the slits.
(a) When the distance between the slits, i. e. d is reduced then p will increase. The interference pattern will thus become broader.
(b) When the entire set up is immersed in water, the pattern will become narrow due to the decrease in the wavelength of light. The new wavelength λ’ = λ/n, hence β’= β/n

Question 11.
Discuss the intensity of transmitted light when a Polaroid sheet is rotated between two crossed polaroids? (NCERT)
Answer:
Let l0 be the intensity of polarised light after passing through the first polarizer P₁. Then the intensity of light after passing through the second polarizer P₂ will be l = l_o cos² θ

where θ is the angle between pass axes of P₁ and P₂. Since P₁ and P₃ are crossed the angle between the pass axes of P₂ and P₃ will be (π/2 – θ). Hence the intensity of light emerging from P₃ will be

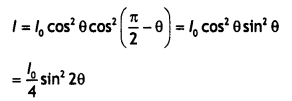
Therefore, the transmitted intensity will be maximum when θ = π/4

Question 12.
A Polaroid (I) is placed In front of a monochromatic source. Another Polaroid (II) is placed in front of this Polaroid (I) and rotated till no light passes. A third Polaroid (III) is now placed in between (I) and (II). In this case, will light emerge from (II)? Explain. (NCERT Exemplar)
Answer:
Only in the special case when the pass axis of (III) is parallel to fill or (II) there shall be no light emerging. In all other cases, there shall be light emerging because the pass axis of (II) is no longer perpendicular to the pass axis of (III).

Question 13.
(a) Good quality sunglasses made of polaroids are preferred over ordinary coloured glasses. Explain why.
(CBSE AI2019)
Answer:
Polaroid sunglasses are preferred over coloured sunglasses because they reduce the intensity of light.

(b) How is plane polarised light defined?
Answer:
Plane polarised light: Light in which vibrations of electric field vector are restricted to one plane containing the direction of propagation.

(c) A beam of plane polarised light is passed through a polaroid. Show graphically, a variation of the intensity of the transmitted light with the angle of rotation of the Polaroid.
Answer:
The graphical variation is as shown.

Wave Optics Important Extra Questions Long Answer Type

Question 1.
Define the term wavefront. Using Huygen’s wave theory, verify the law of reflection.
Or
Define the term, “refractive index” of a medium. Verify Snell’s law of refraction when a plane wavefront is propagating from a denser to a rarer medium. (CBSE Delhi 2019)
Answer:
The wavefront is a locus of points that oscillate in the same phase.

Consider a plane wavefront AB incident obliquely on a plane reflecting surface MM^–. Let us consider the situation when one end A of was front strikes the mirror at an angle i but the other end B has still to cover distance BC. The time required for this will be t = BC/c.

According to Huygen’s principle, point A starts emitting secondary wavelets and in time t, these will cover a distance c t = BC and spread. Hence, with point A as centre and BC as radius, draw a circular arc. Draw tangent CD on this arc from point C. Obviously, the CD is the reflected wavefront inclined at an angle ‘r’. As incident wavefront and reflected wavefront, both are in the plane of the paper, the 1^st law of reflection is proved.

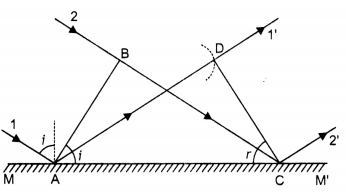
To prove the second law of reflection, consider ΔABC and ΔADC. BC = AD (by construction),
∠ABC = ∠ADC = 90° and AC is common.

Therefore, the two triangles are congruent and, hence, ∠BAC = ∠DCA or ∠i = ∠r, i.e.the angle of reflection is equal to the angle of incidence, which is the second law of reflection.
Or
The refractive index of medium 2, w.r.t. medium 1 equals the ratio of the sine of the angle of incidence (in medium 1) to the sine of the angle of refraction (in medium 2), The diagram is as shown.

From the diagram

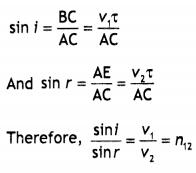
Question 2.
(a) Sketch the refracted wavefront for the incident plane wavefront of the light from a distant object passing through a convex lens.
Answer:

(b) Using Huygens’s principle, verify the laws of refraction when light from a denser medium is incident on a rarer medium.
Answer:
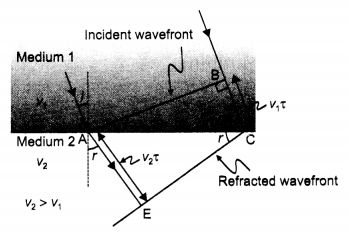
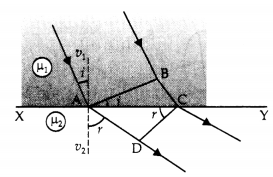
Refraction from denser to the rarer medium: Let XY be plane refracting surface separating two media of refractive index μ₁ and μ₂ (μ₁ > μ₂)

Let a plane wavefront AB incident at an angle i. According to Huygen’s principle, each point on the wavefront becomes a source of secondary wavelets and

Time is taken by wavelets from B to C = Time taken by wavelets from A to D


(c) For yellow light of wavelength 590 nm incident on a glass slab, the refractive index of glass Is 1.5. Estimate the speed and wavelength of yellow light Inside the glass slab. (CBSE 2019C)
Answer:
Given λ = 590 nm, μ = 1.5
Velocity of light inside glass slab.
∴ v = \(\frac{C}{\mu}=\frac{3 \times 10^{8}}{1.5}\) = 2 × 10⁸ ms^-1

Wavelength of yellow light inside the glass slab.
λ₁ = \(\frac{\lambda}{\mu}=\frac{290}{1.5}\) = 393.33 nm

Question 3.
(a) State the postulates of Huygen’s wave theory.
Answer:
The postulates are
All points on a given wavefront are taken as point sources for the production of spherical secondary waves, called wavelets, which propagate outward with speed characteristic of waves in that medium.

(b) Draw the type of wavefront that corresponds to a beam of light (i) coming from a very far off the source and (ii) diverging from a point source.
Answer:
After some time has elapsed, the new position of the wavefront is the surface tangent to the wavelets or the envelope of the wavelets in the forward direction.


Question 4.
What is meant by the diffraction of light? Obtain an expression for the first minimum of diffraction.
Answer:
The divergence of light from its initial line of travel when it passes through an opening or an obstacle is called diffraction or the phenomenon of bending of light around the sharp corners and spreading into the regions of the geometrical shadow is called diffraction.

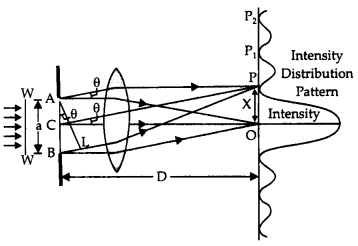
Consider that a monochromatic source of light S, emitting light waves of wavelength λ, is placed at the principal focus of the convex lens L₁. A parallel beam of light, i.e. a plane wavefront, gets incident on a narrow slit AB of width ‘a’ as shown in the figure.

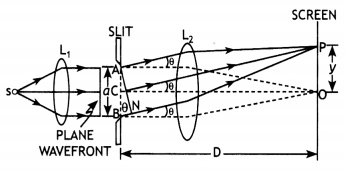
The diffraction pattern is obtained on a screen Lying at a distance D from the slit and at the focal plane of the convex lens L₂.

Consider a point P on the screen at which wavelets travelLing in a direction making angle O with CO are brought to focus by the lens. The wavelets from different parts of the slit do not reach point P in phase, although they are initially in phase. It is because they cover unequal distances in reaching point R The waveLets from points A and B will have a path difference equal to BN.

From the right angLed ANB, we have
BN = AB sin θ or BN = a sin θ …(1)

Suppose that the point P on the screen is at such a distance from the centre of the screen that BN = λ. and the angle θ = θ₁.

Then, equation 1 gives
λ = a sin θ₁ or sin θ₁ = \(\frac{λ}{a}\)

Such a point one screen will be the position of the first secondary minimum.

Question 5.
Describe an experiment to show that light waves are transverse in nature.
Answer:
Light is a transverse wave. This can be shown with the help of this simple experiment. The figure shows an unpolarized light beam incident on the first polarising sheet, called the polariser where the transmission axis is indicated by the straight line on the polariser.

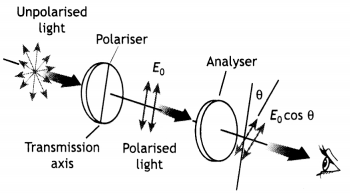
The polariser can be a thin sheet of tourmaline (a complex boro-silicate). The Light, which is passing through this sheet, is polarised vertically as shown, where the transmitted electric vector is E_o. A second polarising sheet called the analyser intercepts this beam with its transmission axis at an angle θ to the axis of the polariser. As the axis of the analyser is rotated slowly, the intensity of Light received beyond It goes on decreasing.

When the transmitting axis of the analyser becomes perpendicular to the transmission axis of the polariser, no beam is obtained beyond the analyser. This means that the anaLyser has further polarised the beam coming from the polariser. Since only transverse waves can be polarised, therefore, this shows that light waves are transverse In nature.

Question 6.
Derive an expression for the width of the central maxima for diffraction of light at a single-slit. How does this width change with an increase in the width of the slit?
Answer:
The width of the central maxima for diffraction of light at a single-slit is the distance from the 1st diffraction minima on one side of the central maxima to the 1st diffraction minima on another side of the central maxima.

If a be the width of slit then for 1st diffraction minima, we have
sin θ = ± λ
or
sin θ = θ = ± \(\frac{λ}{a}\)

Angular width of central maxima
= 2θ = ± \(\frac{2λ}{a}\)

If D be the distance between the slit and the screen, then linear width ‘x’ of the central maxima is given by
x = d × 2θ = D × \(\frac{2λ}{a}\) = \(\frac{2Dλ}{a}\)

As the width (a) of the slit is increased, the linear width of central maxima goes on decreasing because x ∝ \(\frac{1}{a}\)

Question 7.
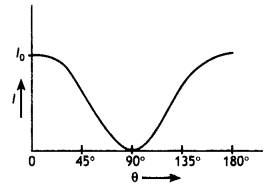
(a) Sketchthegraphshowingthevariation of the intensity of transmitted light on the angle of rotation between a polarizer and an analyser.
Answer:
The graph is as shown below

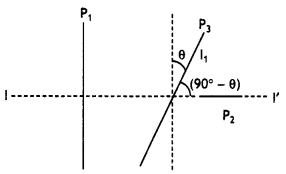
(b) A ray of light is incident at an angle of incidence i_p on the surface of separation between air and a medium of refractive index µ, such that the angle between the reflected and refracted ray is 90°. Obtain the relation between i_p and µ.
Answer:
Suppose an unpolarised light beam is an incident on a surface as shown in the figure below. The beam can be described by two electric field components, one parallel to the surface (the dots) and the other perpendicular to the first and to the direction of propagation (the arrows). It is found that the parallel components reflect more strongly than the other component, this results in a partially polarised beam. Furthermore, the refracted ray is also partially polarized.

Now suppose the angle of incidence, i is varied until the angle between the reflected and the refracted beam is 90°. At this particular angle of incidence, the reflected beam is completely polarised with its electric vector parallel to the surface, while the refracted beam is partially polarised. The angle of incidence at which this occurs is called the polarising angle i_p.

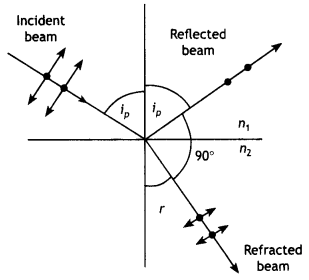
An expression can be obtained relating the polarising angle to the index of refraction n, of the reflecting surface. From the figure, we see that at the polarising angle
i_p + 90° + r = 180°
or
r = 90° – i_p.

Using Snell’s law we have n = \(\frac{\sin i}{\sin r}=\frac{\sin i_{p}}{\sin r}\)

Now sin r = sin (90° – i_p) = cos i_p, therefore the above expression becomes
n = \(\frac{\sin i_{p}}{\cos i_{p}}\) = tan ip

Question 8.
Describe Young’s double-slit experiment to produce an interference pattern due to a monochromatic source of light. Deduce the expression for the fringe width. (CBSE Delhi 2011)
Answer:
Consider a point P on the viewing screen; the screen is Located at a perpendicular distance D from the screen containing the slits S₁ and S₂, which are separated by a distance d as shown in the figure. Let us assume that the source of tight is monochromatic having a waveLength X. Under these conditions, the waves emerging from S and S have the same frequency and amplitude and are In phase.

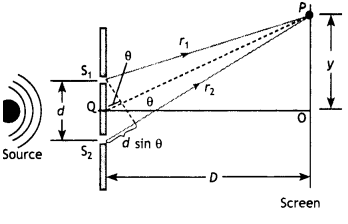
If δ is the path difference between the waves from slits S₂ and S₁ at point P then
δ = r₂ – r₁ = d sin θ …(1)

where it is assumed that r1 and r2 are parallel, which is approximately true because D is much greater than d.

If this path difference is either zero or some Integral multiple of the wavelength, the waves are in phase at P and constructive Interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
δ = d sin θ = m λ …(2)

Here m is called the order number. In order to find the position of maxima measured vertically from O to P, i.e. y we assume that D >> d, that is, the distance from the slits to the screen is much larger than the distance between the two slits. (In practice D = 1 m and d = a few millimetre) Under these conditions, θ is small, and so the approximation sin θ ≈ tan θ. Therefore, from triangle POQ in the figure, we find that
sin θ = tan θ = \(\frac{Y}{D}\) …(3)

Substituting this in equation (2) we have
d \(\frac{Y}{D}\) = m λ …(2)

rewriting the above equation we have
y = \(\frac{mDλ}{d}\) …(4)
This gives the distance of the mth maxima from the centre 0 of the screen. For m = 0, 1, 2, 3, 4, ……. the values of y are
y_o = 0 …….. position of the central bright fringe

y₁ = \(\frac{Dλ}{d}\) ……. position of the first bright fringe

y₂ = \(\frac{2Dλ}{d}\) ……. position of the second bright fringe

y_m = \(\frac{mDλ}{d}\) …….position of the mth bright fringe

The spacing between any two bright fringes gives the width of a dark fringe. Therefore,

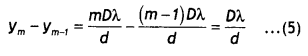
This gives the width of the dark fringe. Similarly, when the path difference is an odd multiple of λ/2, the waves arriving at P will be 180° out of phase and will give rise to destructive interference. There¬fore, the condition for dark fringes, or de¬structive interference, at P is given by

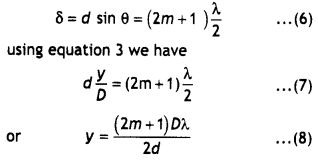
This gives the distance of the mth minima from the centre O of the screen. For m is equal to 0, 1, 2, 3, ……. we have
y’_o = \(\frac{Dλ}{2d}\), ……. position of the first dark fringe,
y’₁ = \(\frac{3Dλ}{2d}\) ……. position of the second dark fringe
y’₂ = \(\frac{5Dλ}{2d}\) ……. position of the third dark fringe and,
y’_m = \(\frac{(2 m+1) D \lambda}{2 d}\) ……. position of the mth dark fringe

Now the spacing between two consecutive dark fringes gives the width of the bright fringe, therefore, a width of the bright fringe is

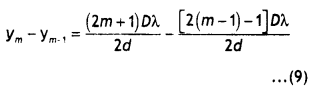
From equations 5 and 9 we find that the fringe width of the bright and the dark fringe is the same, therefore, the fringe width is given by
β = \(\frac{Dλ}{d}\) …(10)

Question 9.
(a) Explain, with the help of a diagram, how plane polarised light Is obtained by scattering.
Answer:
It is found that when unpolarised sunlight is incident on a small dust particle or air molecules it is scattered in all directions. The light scattered in a direction perpendicular to the incident light is found to be completely polarised.

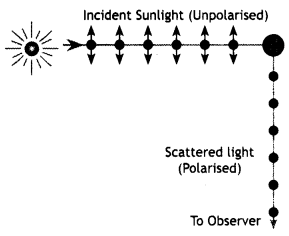
The electric vector of incident light has components both in the plane of the paper as well as perpendicular to the plane of the paper. The electrons under the influence of the electric vector acquire motion in both directions. However, radiation scattered by the molecules in perpendicular direction contains only components represented by dots (.), i.e. polarised perpendicular to the plane of the paper.

(b) Between two polaroids placed In crossed position a third Polaroid is introduced. The axis of the third Polaroid makes an angle of 30° with the axis of the first polaroid. Find the intensity of transmitted light from the system assuming / to be the intensity of polarised light obtained from the first polaroid. (CBSE A! 2011C)
Answer:
Let l_o be the intensity of light passing through the first polaroid.

The intensity of light passing through the middle polaroid whose axes are inclined at 30° to the first polaroid by Malus law is
l’ = l_o cos² 30° = l_o × 3/4 = 3l_o/4

The intensity of light passing through the system is, therefore, (for the second crystal θ = 60°)
l” = l’cos² 60° = 3l_o/4 × 1 /4
or
l” = 3l_o/16

Question 10.
(a) Why are coherent sources necessary to produce a sustained interference pattern?
Answer:
Interference will be sustained if there is a constant phase difference between the two interfering waves. This is possible if the two waves are coherent.

(b) In Young’s double-slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference Is λ, is K units. Find out the intensity of light at a point where the path difference is λ/3. (CBSE Delhi 2012)
Answer:
Intensity at any point on the screen
l = l₁ + l₂ + 2\(\sqrt{1_{1}1_{2}}\) cos Φ

Let l0 be the intensity of either source, then l₁= l₂ = l_o
When p = λ, Φ = 2π

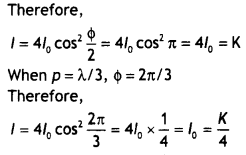
Question 11.
Use Huygen’s principle to explain the formation of the diffraction pattern due to a single-slit illuminated by a monochromatic source of light.
When the width of the slit is made double the original width, how would this affect the size and intensity of the central diffraction band? (CBSE Delhi 2012)
Answer:
(a) The arrangement is shown below in the figure.

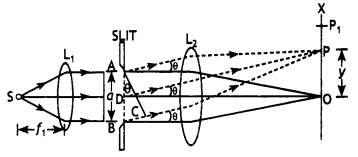
When a plane wavefront WW’ falls on a single-slit AB, each point on the unblocked portion ADB of wavefront sends out secondary, wavelets in all the directions. For secondary waves meeting at point O, the path difference between waves is zero and hence the secondary waves reinforce each other giving rise to the central maximum at the symmetrical point O.

Consider secondary waves travelling in a direction making an angle θ with DO and reaching the screen at point P. Obviously, path difference between the extreme secondary waves reaching point P from A and B.
= BC = AB sin θ = a sin θ.

If this path difference a sin θ = λ, then point P will be minimum Intensity. In this situation, wavefront may be supposed to consist of two equal halves AD and BD and for every point on AD, there will be a corresponding point on DB having a path difference λ/2. Consequently, they nullify the effect of each other and point P behaves as the first secondary minimum. In general, if path difference a sin θ = nλ where n = 1, 2, 3, …. then we have secondary minima corresponding to that angle of diffraction θ_n.

However, if for some point P₁ on the screen secondary waves BP₁ and AP₁ differ In path by 3λ/2 then point P₁ will be the position of the first secondary maxima. Because in this situation, wavefront AB may be divided into three equal parts such that path difference between corresponding points on the first and second will be λ/2 and they will nullify. But secondary waves from the third part remain as such and give rise to the first secondary maxima, whose Intensity will be much less than that of central maxima.

In general, if path difference a sin θ = (2n + 1)θ/2, where n = 1, 2, 3, …… then we have nth secondary maxima corresponding to these angles.

The width of the central maxima is the distance between the first secondary minima on either side of the centre of the screen. The width of the central maxima is twice the angle θ subtended by the first minima on either side of the central maxima. Now sin θ = \(\frac{\lambda}{a}\). Since θ is small a therefore it can be replaced by tan θ, hence sin θ = \(\frac{\lambda}{a}=\frac{y}{L} or y = [latex]\frac{L \lambda}{\mathrm{a}}\).

This gives the distance of the first secondary minima on both sides of the centre of the screen. Therefore, the width of the central maxima is 2y, hence
2y = \(\frac{2L \lambda}{\mathrm{a}}\)

(b) The size reduces by half according to the relation: size = X/d. Intensity becomes twice the original intensity.

Question 12.
(a) Using the phenomenon of polarization, show how the transverse nature of light can be demonstrated.
Answer:
Light is a transverse wave. This can be shown with the help of this simple experiment. The figure shows an unpolarized light beam incident on the first polarising sheet, called the polariser where the transmission axis is indicated by the straight line on the polariser.

The polariser can be a thin sheet of tourmaline (a complex boro-silicate). The Light, which is passing through this sheet, is polarised vertically as shown, where the transmitted electric vector is E_o. A second polarising sheet called the analyser intercepts this beam with its transmission axis at an angle θ to the axis of the polariser. As the axis of the analyser is rotated slowly, the intensity of Light received beyond It goes on decreasing.

When the transmitting axis of the analyser becomes perpendicular to the transmission axis of the polariser, no beam is obtained beyond the analyser. This means that the anaLyser has further polarised the beam coming from the polariser. Since only transverse waves can be polarised, therefore, this shows that light waves are transverse in nature.

(b) Two polaroids P₁ and P₂ are placed with their pass axes perpendicular to each other. Unpolarised light of intensity l0 is Incident on P₁. A third polaroid P₃ is kept in between P₁ and P₂ such that its pass axis makes an angle of 30° with that of P₁. Determine the intensity of light transmitted through P₁ P₂ and P₃. (CBSE AI 2014)
Answer:
The intensity of light passing through P₁ is half of the light falling on it. Therefore, the light coming out of P₁ is l0_o/2 Now light coming out of P₃ is

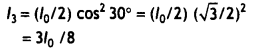
and light coming out of polariser P₂ is

Question 13.
What does a Polaroid consist of? Show using a simple Polaroid that light waves are transverse in nature. The intensity of light coming out of a Polaroid does not change irrespective of the orientation of the pass axis of the polaroid. Explain why. (CBSE AI 2015)
Answer:
A polaroid consists of long-chain molecules aligned in a particular direction.

Let the light from an ordinary source (like a sodium lamps pass through a polaroid sheet P₁ it is observed that its intensity is reduced by half. Now, let an identical piece of polaroid P₂ be placed before P₁ As expected, the light from the lamp is reduced in intensity on passing through P₂2 alone. But now rotating P₁ has a dramatic effect on the light coming from P₂. In one position, the intensity transmitted by P₂ followed by P₁ is nearly zero. When turned by 90° from this position, P₁ transmits nearly the full intensity emerging from P₂ shown in the figure.

Since only transverse waves can be polarised, therefore, this experiment shows that light waves are transverse in nature. The electric vectors (associated with the propagating light wave) along the direction of the aligned molecules get absorbed. Thus, if an unpolarized light wave is an incident on such a polaroid then the light wave will get linearly polarized with the electric vector oscillating along a direction perpendicular to the aligned molecules; this direction is known as the pass-axis of the Polaroid.

Thus, if the light from an ordinary source (like a sodium lamp) passes through a polaroid sheet P it is observed that its intensity is reduced by half. Rotating P has no effect on the transmitted beam and transmitted intensity remains constant as there is always an electric vector that oscillates in a direction perpendicular to the direction of the aligned molecules.

Question 14.
Find an expression for intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids. In which position of the polaroid sheet will the transmitted Intensity be maximum? (CBSE Delhi 2015)
Answer:
Let l0 be the intensity of polarised light after passing through the first polarizer P₁. Then the intensity of light after passing through the second polarizer P₂ will be
l = l_o cos² θ

where θ is the angle between pass axes of P₁ and P₂. Since P₁ and P₃ are crossed the angle between the pass axes of P₂ and P₃ will be (π/2 – θ). Hence the intensity of light emerging from P₃ will be

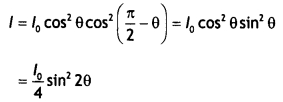
The transmitted intensity will be maximum when 2θ = π/2 or θ = π/4

Question 15.
Distinguish between unpolarised and linearly polarised light. Describe with the help of a diagram how unpolarised light gets linearly polarised by scattering. (CBSE Delhi 2015)
Answer:
The two lights will be allowed to pass through a polariser. When the polarizer is rotated in the path of these two light beams, the intensity of light remains the same in all the orientations of the polariser, then the light is unpolarised. But if the intensity of light varies from maximum to minimum then the light beam is a polarised light beam.

It is found that when unpolarised sunlight is incident on a small dust particle or air molecules it is scattered in all directions. The light scattered in a direction perpendicular to the incident light is found to be completely polarised.

The electric vector of incident light has components both in the plane of the paper as well as perpendicular to the plane of the paper. The electrons under the influence of the electric vector acquire motion in both directions. However, radiation scattered by the molecules in perpendicular direction contains only components represented by dots (.), i.e. polarised perpendicular to the plane of the paper.

Question 16.
(a) Explain how a diffraction pattern is formed due to interference of secondary wavelets of light waves from a slit.
Answer:
(a) Diffraction at single slit: Consider monochromatic plane wavefront WW’ incident on the slit AB as shown in Fig. Imagine the slit to be divided into a large number of very narrow strips of equal width parallel to the slit. When the wavefront reaches the slit, each narrow strip parallel to the slit can be considered to be a source of Huygen’s secondary wavelets.

Central Maxima. Let us first consider the effect of all the wavelets at point O. All wavelets cover the same distance and reach 0 in the same phase. The wavelets superimpose constructively and give maximum intensity at O.

Position of secondary minima. Consider the intensity at a point P at an angle θ with the original direction.
Draw AL ⊥ BP.
In ΔABL


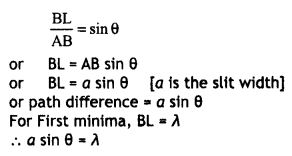
or
sin θ = \(\frac{λ}{a}\)

For second minima, BL = 2A
or a sin θ = 2λ

Similarly, for nth minima a sin θ = nλ
or sin θ = \(\frac{nλ}{a}\) , where n = 1, 2, ……

Position of secondary maxima: If path difference BL = \(\frac{3λ}{2}\), then slit AB can be divided into three equal parts and the path difference between wavelets from corresponding points in the first two parts will be \(\frac{λ}{2}\) and hence cancels each other’s effect and produces destructive Interference and the third path will produce its maxima at P called first secondary maxima.

Similarly, if BL = \(\frac{5λ}{2}\), we get second secondary maxima and so on.

For nth maxima
a sin θ = (2n + 1)\(\frac{λ}{a}\)
or
sin θ = \(\frac{(2 n+1) \lambda}{2 a}\)

Thus we find that the intensity of the central fringe is maximum whereas that of other fringes fall off rapidly in either direction from the centre of the fringe pattern.

(b) Sodium light consists of two wavelengths, 5900 Å and 5960 Å. If a slit of width 2 × 10^-4 m is Illuminated by sodium light, find the separation between the first secondary maxima of the diffraction pattern of the two wavelengths on a screen placed 1.5m away. (CBSE 2019C)
Answer:
The separation between the first secondary maxima of the diffraction pattern of two wavelengths is:

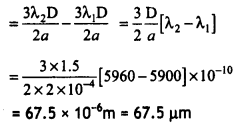
Question 17.
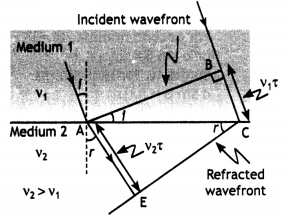
(a) Derive Snell’s law on the basis of Huygen’s wave theory when light Is travelling from a denser to a rarer medium.
Answer:
The ray diagram is as shown.


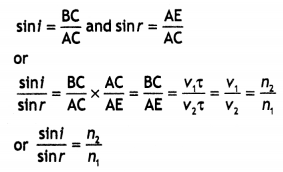
(b) Draw the sketches to differentiate between plane wavefront and spherical wavefront. (CBSE AI 2016)
Answer:
Spherical wavefront and plane wavefront

Question 18.
The figure drawn here shows the geometry of path differences for diffraction by a single-slit of width a.

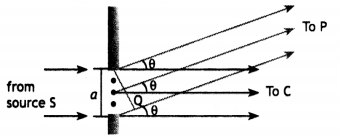
Give appropriate ‘reasoning’ to explain why the intensity of light is
(a) Maximum at the central point C on the screen.
(b) (Nearly) zero for point P on the screen when θ = λ / a.
Hence write an expression for the total linear width of the central maxima on a screen kept at a distance D from the plane of the slit. (CBSE Delhi 2016C)
Answer:
(a) At central point C, the angle is zero, all path differences are zero. Hence all the parts of the slit contribute to the same phase. This gives the maximum intensity at point C.
(b)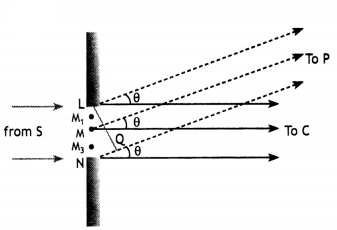

From figure
NP – LP = NQ= a sin θ = aθ When θ = λ/a

Then path difference NP – LP = aθ = λ.
Hence MP – LP = NP – MP = λ/2

It implies that the contribution from corresponding points in two halves of the slit has a phase difference of π. Therefore, contributions from two halves cancel each other in pairs, resulting in a zero net intensity at point P on the screen. Half angular width of central maxima = λ/a Half linear width = λD/a

Linear width of central maxima = 2λD/a

Question 19.
Two polaroids, P₁ and P₂, are ‘set-up’ so that their ‘pass axis is ‘crossed’ with respect to each other. AQ third Polaroid, P₃ is now introduced between these two so that its ‘pass axis makes an angle with the ‘pass axis of P_1. A beam of unpolarized light, of Intensity I, Is Incident on P₁ If the Intensity of light that gets transmitted through this combination of three polaroids, Is I’, find the ratio \(\left(\frac{I^{\prime}}{I}\right)\) when θ equals: (i) 30°, (ii) 45° (CBSE Delhi 2016C)
Answer:
The diagram is as shown.

The intensity of unpolarized light is given as l.
It becomes half after passing through Polaroid P₁ (l/2)
Using Malus law for the intensity of light passing through P3 we have
l₁ = \(\left(\frac{l}{2}\right)\) cos²θ

This intensity l₁ is Incident on P₂, hence the intensity of light coming out of P₂ will be

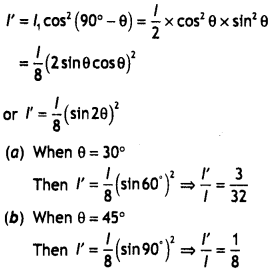
Question 20.
What is the effect on the Interference pattern observed In Young’s double-slit experiment In the following cases:
(a) Screen is moved away from the plane of the slits,
(b) Separation between the slits is Increased and
(c) Widths of the slits are doubled. Give the reason for your answer.
Answer:
The fringe width is given by the expression
β = \(\frac{Dλ}{d}\)

(a) When D Is Increased, the fringe width Increases.
(b) When d 1s Increased the fringe width decreases.
(c) If the width w of the slits Is changed then Interference occurs only If \(\frac{1}{w}\) > \(\frac{1}{d}\) remains satisfied, where d is the distance between the slits.

Question 21.
Two slits In Young’s double-slit experiment are illuminated by two different lamps emitting light? Will you observe the Interference pattern? Justify your answer. Find the ratio of Intensities at two points on a screen In Young’s double-slit experiment, when waves from two slits have a path difference of (i) 0 and (ii) λ/4.
Answer:
The two sources act as Independent sources of light and hence can never be coherent. In a light, source light is produced by billions of atoms under proper excitation condition and each atom acts independently of the other atoms. Thus there Is no coherence ‘ between these two Independent sources hence no interference.

The phase difference corresponding to the two paths are Φ = 0 and Φ = π/2

Now intensity at the screen when the phase difference is Φ = 0 is
l_A = l₁ +l₂ + 2\(\sqrt{l_{1} l_{2}}\)cos Φ
or
l_A = l + l + 2\(\sqrt{l l}\)cos Φ = 4l

Now intensity at the screen when the phase difference is Φ = 90° Is
l_B = l₁ +l₂ + 2\(\sqrt{l_{1} l_{2}}\)cos Φ
or
l_B = l + l + 2\(\sqrt{l l}\)cos 90° = 2l
Therefore, ratio of intensities is
\(\frac{l_{A}}{l_{B}}=\frac{4l}{2l}\) = 2

Question 22.
(a) In a single-slit diffraction pattern, how does the angular width of the central maximum vary, when
(i) the aperture of the slit Is Increased?
(ii) distance between the slit and the screen is decreased?
Justify your answer In each case.
Answer:
The angular width of the central maxima in a single-slit diffraction pattern is given by 2θ = \(\frac{2λ}{a}\) where λ is the wavelength of light and ‘a’ the slit width.
(i) When the aperture of the slit is increased the angular width decreases.
(ii) When the distance between the slit and the screen is decreased, the angular width will remain the same but the linear width will increase.

(b) How Is the diffraction pattern different from the interference pattern obtained In Young’s double¬slit experiment? (CBSE Delhi 2011C)
Answer:
The difference is shown in the table:

Diffraction	Interference
1. It is due to interference between the wavelets starting from two parts of the same wavefront.	1. It is a superposition of the two waves starting from two coherent sources.
2. The intensity of the consecutive bands goes on decreasing.	2. All bright fringes have the same intensity.
3. Fringes have poor contrast.	3. Fringes have good contrast.
4. Diffraction fringes are not of the same width.	4. Fringes may or may not be of the same width.

Question 23.
(a) Can two independent monochromatic light sources be used to obtain a steady interference pattern? Justify your answer. (CBSE 2019C)
Answer:
No, because the phase difference between the light waves from two independent sources keeps on changing continuously and for a steady interference pattern, the phase difference between the waves should remain constant with time. Hence two independent monochromatic light sources cannot produce a steady interference pattern.

(b) In Young’s double-slit experiment, explain the formation of interference fringes and obtain an expression for the fringe width.
Answer:
Interference of light

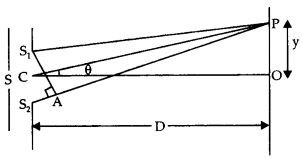
Let S₁, S₂ be the two fine slits illuminated by a monochromatic source S of wavelength λ.

The intensity of light at any point P on the screen at a distance D from the slit depends upon the path difference between S₂P and S₁P.
∴ Path difference = S₂P – S₁P
= (S₂A + AP) – S₁P

Path difference = S₂A = d sin θ
Since θ is small, sin θ can be replaced by tan θ.
∴ Path difference = d tan θ = d\(\frac{y}{D}\)

Constructive interference [Bright Fringes]. For bright fringes, the path difference should be equal to integral multiple of A.
∴ \(\frac{dy}{D}\) = nλ
or
y = n\(\frac{λD}{d}\)

For nth fringe, let us write y as y_n
so y_n = n\(\frac{λD}{d}\)

The spacing between two consecutive bright fringes is equal to the width of a dark fringe.
∴ Width of the dark fringe.
β = y_n – y_n-1 = \(\frac{nλD}{d}\) – (n – 1)\(\frac{λD}{d}\) = \(\frac{λD}{d}\) …(i)

Destructive interference. [Dark Fringes].
For dark fringes, the path difference should be an odd multiple of λ/2.
∴ \(\frac{d}{D}\)y = (2n + 1)λ/2
or
y’ = \(\frac{D}{d}\)(2n + 1)\(\frac{λ}{2}\) = \(\frac{(2 n+1) \lambda D}{2 d}\)

For nth fringe, writing y as yn, we get
y’_n = \(\frac{(2 n+1) \lambda D}{2 d}\).

The spacing between two consecutive dark fringes is equal to the width of a bright fringe.
∴ Width of the bright fringe.

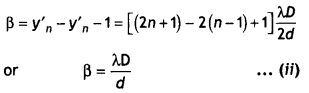
From Eqs. (i) and (ii), we find that dark and bright fringes are of same width given by
β = \(\frac{λD}{d}\).

(c) In an interference experiment using monochromatic light of wavelength A, the intensity of light of point, where the path difference is X, on the screen is K units. Find out the Intensity of light at a point when path difference is λ/4. (CBSE 2019C)
Answer:
The intensity of light on the screen where the waves meet having phase difference Φ is:


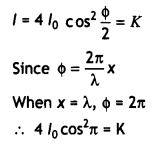
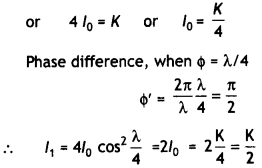
Question 24.
(a) Two monochromatic waves emanating from two coherent sources have the displacements represented by y₁ = a cos ωt and y₂ = a cos (ωt + Φ), where Φ is the phase difference between the two displacements. Show that the resultant intensity at a point due to their superposition is given by l = 4l_o cos² Φ/2, where l_o = a².
Answer:
Let the displacements of the waves from the sources S₁ and S₂ at a point on the screen at any time t be given by y₁ = a cos ωt and y₂ = a cos (ωt + Φ), where Φ is the constant phase difference between the two waves. By the superposition principle, the resultant displacement at point P is given by

Thus the amplitude of the resultant displacement is A = 2a cos (Φ/2)

Therefore the intensity at that point is
l = A² = 4a² cos² \(\frac{Φ}{2}\)

(b) Hence obtain the conditions for constructive and destructive interference. (CBSE AI 2014C)
Answer:
Bright fringes: For bright fringes I = max, therefore Φ = 0° or cos Φ = +1
or
Φ = 2 n π
Dark fringes: For dark fringes l = 0,
therefore Φ = π or cos Φ = -1
or
Φ = (2n + 1) π

Question 25.
A parallel beam of monochromatic light falls normally on a narrow slit of width ‘a’ to produce a diffraction pattern on the screen placed parallel to the plane of the slit. Use Huygens’ principle to explain that
(a) the central bright maxima is twice as wide as the other maxima.
Answer:
The width of the central maxima is the distance between the first secondary minima on either side of the centre of the screen. The width of the central maxima is twice the angle 6 subtended by the first minima on either side of the central maxima.

Now sin θ = \(\frac{λ}{a}\). Since θ is small there, a fore it can be replaced by tan 0, hence
tan θ = \(\frac{λ}{a}\) = \(\frac{y}{L}\)
or
y = \(\frac{Lλ}{a}\). This gives the distance of the first secondary min¬ima on both sides of the centre of the screen. Therefore, the width of the central maxima is 2y, hence
2y = \(\frac{2Lλ}{a}\)

(b) the Intensity falls as we move to successive maxima away from the centre on either side. (CBSE Delhi 2014C)
Answer:
The maxima in diffraction pattern are formed at (n +1 /2) λ/a, with n = 2, 3, etc. These become weaker with increasing n, since only one third, one- fifth, one-seventh, etc., of the slit contributes in these cases.

Question 26.
Answer the following questions:
(a) In a double-slit experiment using the light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
Answer:

(b) Light of wavelength 5000 A propagating 1n air gets partly reflected from the surface of the water. How will the wavelengths and frequencies of the reflected and refracted light be affected? (CBSE Delhi 2015)
Answer:
No change in the wavelength and frequency of reflected light. In the case of refracted light, there is no change in frequency but the wavelength becomes 1/1.33 times the original wavelength.

Question 27.
(a) Good quality sun-glasses made of polaroids are preferred over ordinary coloured glasses. Justify your answer,
Answer:
A Polaroid sun-glass limits the light entering the eye, thus providing a soothing effect.

(b) Two polaroids and P₂ are placed In crossed positions. A third Polaroid P₃ is kept between P₁ and P₂ such that the pass axis of P₃ is parallel to that of P₁. How would the Intensity of light l₂ transmitted through P₂ vary as P₃ Is rotated? Draw a plot of Intensity l₂ Vs the angle ‘θ’, between pass axes of P₁ and P₃. (CBSE AI 2015C)
Answer:
Let l0 be the intensity of polarised light after passing through the first polarizer P₁ Then the intensity of light after passing through the second polarizer P₃ will be
l = l_o cos² θ
where θ is the angle between pass axes of P₁ and P₃. Since P₁ and P₂ are crossed the angle between the pass axes of P₂ and P₃ will be (π/2 – θ).

Hence the intensity of light emerging from P2 will be

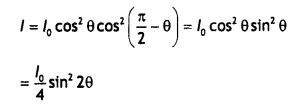
Therefore, the transmitted intensity will be maximum when θ = π/4

For graph

Question 28.
In a single-slit diffraction pattern, how does the angular width of central maximum change, when
(a) slit width is decreased,
(b) distance between the slit and screen is increased, and
(c) light of smaller visible wavelength is used? Justify your answer in each case.
Answer:
We know that the angular width of the central maximum of the diffraction pattern of a single-slit is given by
w = \(\frac{2Dλ}{a}\).

(a) If slit width ‘a’ is decreased, the angular width will increase because
x ∝ \(\frac{1}{a}\)

(b) Increase in distance between the slit and the screen does not affect the angular width of diffraction maxima. However, linear width of the maxima
w = \(\frac{2Dλ}{a}\) will increase.

(c) If the light of a smaller visible wavelength is used, the angular width is decreased because x ∝ λ.

Question 29.
Light, from a sodium lamp, is passed through two polaroid sheets P₁ and P₂ kept one after the other. Keeping P₁ fixed, P₂ is rotated so that its ‘pass axis can be at different angles, θ, with respect to the pass-axis of P₁
An experimentalist records the following data for the Intensity of light coming out of P₂ as a function of the angle θ.

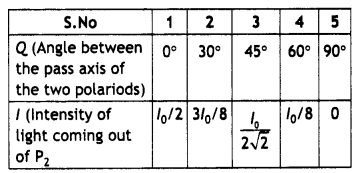
(a) l_o = Intensity of beam falling on P₁ One of these observations is not in agreement with the expected theoretical variation of l, Identify this observation and write the correct expression.
Answer:
The observation \(\frac{l_{0}}{2 \sqrt{2}}\) is not correct. It should be l_o/4.

(b) Define the Brewster angle and write the expression for it in terms of the refractive index of the medium.
Answer:
It is the angle of incidence at which the refracted and the reflected rays are perpendicular to each other. It is related to the refractive index as tan i_p = n

Question 30.
(a) Light, from a monochromatic source, is made to fall on a single-slit of variable width. An experimentalist records the following data for the linear width of the principal maxima ‘ on a screen kept at a distance of 1 m from the plane of the slit.

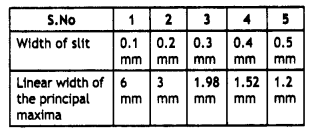
Use any two observations from this data to estimate the value of the wavelength of light used.
Answer:
The width of the central maxima is given by the expression β = \(\frac{2Lλ}{a}\)
or
λ₁ = \(\frac{βa}{2L}\)

Using the values of the first observation we have
λ₁ = \(\frac{6 \times 10^{-3} \times 0.1 \times 10^{-3}}{2 \times 1}\) = 0.3 × 10^-6

Using the values of the second observation we have
λ₁ = \frac{3 \times 10^{-3} \times 0.2 \times 10^{-3}}{2 \times 1} = 0.3 × 10^-6

Thus the wavelength of light used is λ = 0.3 × 10^-6 m

(b) Show that the Brewster angle iB for a given pair of transparent media is related to their critical angle ic through the relation i_c = sin^-1 (ωt i_B)
Answer:
We know that

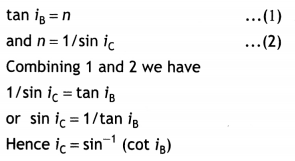
Question 31.
For a single-slit of width, “a” the first minimum of the interference pattern of monochromatic light of wavelength λ occurs at an angle of λ/a. At the same angle λ/a, we get a maximum for two narrow slits separated by a distance ‘a’. Explain. (CBSE Delhi 2014)
Answer:
The path difference between two secondary wavelets is given by nλ = a sin θ. Since θ is a very small sin θ = 0. So, for the first-order diffraction n = 1, the angle is λ/a. Now we know that θ must be very small θ = 0 (nearly) because of which the diffraction pattern is minimum.

Now for interference case, for two interfering waves of intensity l1 and l2 we must have two slits separated by a distance. We have the resultant intensity,
l = l₁ + l₂ + 2\(\sqrt{l_{1} l_{2}}\) cos θ

Since θ = 0° (nearly) corresponding to angle λ/a so cos θ = 1 (nearly)
So,
l = l₁ + l₂ + 2\(\sqrt{l_{1} l_{2}}\) cos θ
l = l₁ + l₂ + 2\(\sqrt{l_{1} l_{2}}\)

We see the resultant intensity is the sum of the two intensities, so there is a maxima corresponding to the angle λ/a.

This is why, at the same angle of λ/a, we get a maximum for two narrow slits separated by a distance “a”.

Question 32.
Show using a proper diagram of how unpolarised light can be linearly polarized by reflection from a transparent glass surface. (CBSE AI 2018, Delhi 2018)
Answer:
An ordinary beam of light, on reflection from a transparent medium, becomes partially polarised. The degree of polarisation increases as the angle of incidence is increased. At a particular value of the angle of incidence, the reflected beam becomes completely polarised. This angle of incidence is called the polarising angle (i_p).

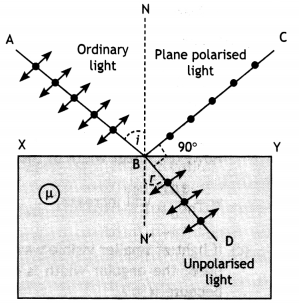
Question 33.
Answer the following questions:
(a) In a single-slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band?
Answer:
The size reduces by half according to the relation: size = λ/d. Intensity increases fourfold.

(b) In what way is diffraction from each slit related to the interference pattern in a double-slit experiment?
Answer:
The intensity of interference fringes in a double-slit arrangement is modulated by the diffraction pattern of each slit.

(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why?
Answer:
Waves diffracted from the edge of the circular obstacle interfere constructively at the centre of the shadow producing a bright spot.

(d) Two students are separated by a 7 m partition wall in a room 10 m high. If both light and sound waves can bend around obstacles, how is it that the students are unable to see each other even though they can converse easily? (NCERT)
Answer:
For diffraction or bending of waves by obstacles/apertures by a large angle, the size of the latter should be comparable to the wavelength. If the size of the obstacle/aperture is much too large compared to the wavelength, diffraction is by a small angle. Here the size is of the order of a few metres. The wavelength of light is about 5 × 10^-7 m, while sound waves of, say, 1 kHz frequency have a wavelength of about 0.3 m. Thus, sound waves can bend around the partition while light waves cannot.

Question 34.
(a) When an unpolarized light of intensity l0 is passed through a polaroid, what is the intensity of the linearly polarised light? Does it depend on the orientation of the polaroid? Explain your answer.
Answer:
(a) The intensity of the linearly polarised light would be l_o/2.
No, it does not depend on the orientation.
Explanation: The polaroid will let the component of the unpolarized light, parallel to its pass axis, to pass through it irrespective of its orientation.

(b) A plane polarised beam of light is passed through a polaroid. Show graphically the variation of the intensity of the transmitted light with an angle of rotation of the polaroid incomplete one rotation. (CBSE Delhi 2018C)
Answer:
We have l = l_o cos² θ
∴ The graph is as shown below

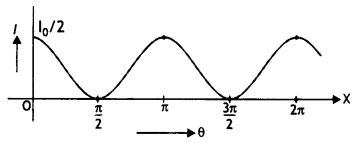
Question 35.
(a) If one of two identical slits producing interference in Young’s experiment is covered with glass so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the Interference pattern.
Answer:
As intensity is directly proportional to the square of the amplitude.


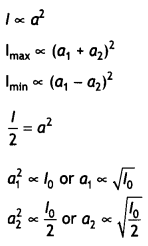
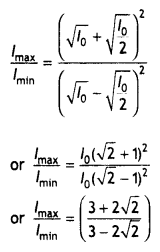
(b) What kind of fringes do you expect to observe if white light is used Instead of monochromatic light?
Answer:
The central fringe will be white and the remaining will be coloured fringes of different width in the VIBGYOR sequence.

Question 36.
Find an expression for intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids. In which position of the polaroid sheet will the transmitted intensity be maximum? (CBSE Delhi 2015)
Answer:
Let l0 be the intensity of polarised light after passing through the first polarizer P₁ Then the intensity of light after passing through the second polarizer P₂ will be
l = l_o cos² θ
where 0 is the angle between pass axes of P₁ and P₂. Since P₁ and P₃ are crossed the angle between the pass axes of P₂ and P3 will be (π/2 – θ). Hence the intensity of light emerging from P₃ will be

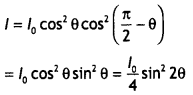
The transmitted intensity will be maximum when 2θ = π/2 or θ = π/4

Question 37.
Derive the expression for the fringe width In Young’s double-slit experiment.
Answer:
Consider a point P on the viewing screen; the screen is Located at a perpendicular distance D from the screen containing the slits S₁ and S₂, which are separated by a distance d as shown in the figure. Let us assume that the source of tight is monochromatic having a waveLength X. Under these conditions, the waves emerging from S and S have the same frequency and amplitude and are In phase.

If δ is the path difference between the waves from slits S₂ and S₁ at point P then
δ = r₂ – r₁ = d sin θ …(1)

where it is assumed that r₁ and r₂ are parallel, which is approximately true because D is much greater than d.

If this path difference is either zero or some Integral multiple of the wavelength, the waves are in phase at P and constructive Interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
δ = d sin θ = m λ …(2)

Here m is called the order number. In order to find the position of maxima measured vertically from O to P, i.e. y we assume that D >> d, that is, the distance from the slits to the screen is much larger than the distance between the two slits. (In practice D = 1 m and d = a few millimetre) Under these conditions, θ is small, and so the approximation sin θ ≈ tan θ. Therefore, from triangle POQ in the figure, we find that
sin θ = tan θ = \(\frac{Y}{D}\) …(3)

Substituting this in equation (2) we have
d \(\frac{Y}{D}\) = m λ …(2)

rewriting the above equation we have
y = \(\frac{mDλ}{d}\) …(4)
This gives the distance of the mth maxima from the centre 0 of the screen. For m = 0, 1, 2, 3, 4, ……. the values of y are
y_o0 = 0 …….. position of the central bright fringe

y₁ = \(\frac{Dλ}{d}\) ……. position of the first bright fringe

y₂ = \(\frac{2Dλ}{d}\) ……. position of the second bright fringe

y_m = \(\frac{mDλ}{d}\) …….position of the mth bright fringe

The spacing between any two bright fringes gives the width of a dark fringe. Therefore,

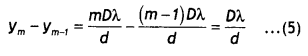
This gives the width of the dark fringe. Similarly, when the path difference is an odd multiple of λ/2, the waves arriving at P will be 180° out of phase and will give rise to destructive interference. There¬fore, the condition for dark fringes, or de¬structive interference, at P is given by

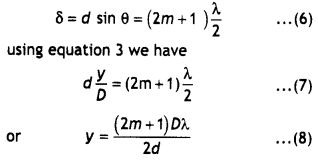
This gives the distance of the mth minima from the centre O of the screen. For m is equal to 0, 1, 2, 3, ……. we have
y’_o = \(\frac{Dλ}{2d}\), ……. position of the first dark fringe,

y’₁ = \(\frac{3Dλ}{2d}\) ……. position of the second dark fringe

y’₂ = \(\frac{5Dλ}{2d}\) ……. position of the third dark fringe and,

y’_m = \(\frac{(2 m+1) D \lambda}{2 d}\) ……. position of the mth dark fringe

Now the spacing between two consecutive dark fringes gives the width of the bright fringe, therefore, a width of the bright fringe is

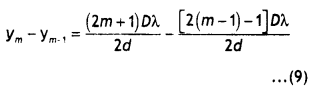
From equations 5 and 9 we find that the fringe width of the bright and the dark fringe is the same, therefore, the fringe width is given by
β = \(\frac{Dλ}{d}\) …(10)

Question 38.
(a) Using Huygens’ principle, draw a diagram to show the propagation of a wave-front originating from a monochromatic point source.
Answer:

(b) Describe diffraction of light due to a single-slit. Explain the formation of a pattern of fringes obtained on the screen and plot showing a variation of intensity with path difference in single-slit diffraction.
Answer:
Let us discuss the nature of the Fraunhofer diffraction pattern produced by a single-slit. Let us examine the waves coming from the various portions of the slit, as shown in the figure. According to Huygens principle, each portion of the slit acts as a source of waves. Hence, light from one portion of the slit can interfere with the light of another portion, and the resultant intensity on the screen will depend on the direction of θ. The secondary waves coming from the different parts of the slit interfere to produce either maxima or minima, thereby giving rise to a diffraction pattern.

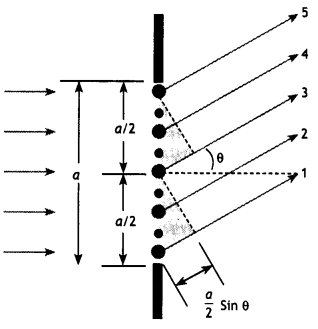
For the diagram

2y = \(\frac{2Lλ}{a}\)

Question 39.
What is the effect on the interference fringes in Young’s double-slit experiment due to each of the following operations:
(a) the screen is moved away from the plane of the slits;
Answer:
The angular separation of the fringes remains constant (= λ/d). The actual separation of the fringes increases in proportion to the distance of the screen from the plane of the slits

(b) the (monochromatic) source is replaced by another (monochromatic) source of shorter wavelength;
Answer:
The separation of the fringes (and also angular separation) decreases.

(c) the separation between the two slits is Increased
Answer:
The separation of the fringes (and also angular separation) decreases.

(d) the source slit is moved closer to the double-slit plane;
Answer:
Let s be the size of the source and S its distance from the plane of the two slits. For interference, fringes to be seen the
condition \(\frac{s}{S}<\frac{\lambda}{d}\) should be satisfied otherwise interference patterns produced by different parts of the source overlap and no fringes are seen. Thus as S decreases (i.e. the source slit is brought closer), the interference pattern gets less and less sharp and when the source is brought too close for this condition to be valid the fringes – disappear. Till this happens, the fringe separation remains fixed.

(e) the width of the source slit is Increased;
Answer:
Same as in (d). As the source slit width increases fringe pattern gets less and less sharp. When the source slit is so wide that the condition \(\frac{s}{S}<\frac{\lambda}{d}\) is not satisfied the interference pattern disappears.

(f) the monochromatic source is replaced by a source of white light? (In each operation take all parameters other than the one specified to remain unchanged.)
Answer:
The interference patterns due to different component colours of white light overlap (incoherently). The central bright fringes for different colours are in the same position. Therefore, the central fringe is white. For a point P for which S₂P – S₁P= λ_b /2, where (λ_b = 400 nm) represents the wavelength for the blue colour, the blue component will be absent and the fringe will appear red in colour. Slightly farther away from where S₂Q – S₁Q = λ_b = λ_r/2 where λ_r (800 nm) is the wavelength for the red colour, the fringe will be predominantly blue. Thus, the fringe closest on either side of the central white fringe is red and the farthest will appear blue. After a few fringes, no clear fringe pattern is seen.

Question 40.
What is the diffraction of light? Draw a graph showing the variation of intensity with the angle in a single-slit diffraction experiment. Write one feature which distinguishes the observed pattern from the double-slit interference pattern. How would the diffraction pattern of a single-slit be affected when:
(i) the width of the slit is decreased?
(ii) the monochromatic source of light is replaced by a source of white light?
Answer:
Diffraction is the bending of light around obstacles or openings. It is a consequence of the wave nature of light. For diffraction to take place the obstacle should be of the order of the wavelength of light.

The intensity distribution for the single-slit diffraction pattern is as shown.

The intensity of all bright fringes is the same in Young’s interference pattern, but in diffraction, the intensity of bright fringes falls off on both sides of the central fringe.
We know that the angular width of the central maximum of the diffraction pattern of a single-slit is given by = \(\frac{2Dλ}{a}\)
(i) If slit width ‘a’ is decreased, the angular width will increase because
x ∝ \(\frac{1}{a}\)

(ii) When monochromatic light is replaced by white light, all the seven wavelengths form their own diffraction pattern, so coloured fringes are formed. The first few fringes are visible but due to overlapping the clarity of fringes decreases as the order increases.

Question 41.
(a) Define a wavefront. Using Huygens’ geometrical construction, explain with the help of a diagram how the plane wavefront travels from the instant t₁ to t₂ in the air.
Answer:
(a) Wavefront: It is the locus of the medium or points of a medium that is in the same phase of disturbance
First, consider a plane wave moving through free space as shown in the figure. At t = 0, the wavefront is indicated by the plane labelled AA’. In Huygens’s construction, each point on this wavefront is considered a point source. For clarity, only a few points on AA’ are shown. With these points as sources for the wavelets, we draw circles each of radius cΔt, where c is the speed of light in free space and Δt is the time of propagation from one wavefront to the next. The surface drawn tangent to these wavelets is the plane BB’, (Wavefront at a later time t). Here A₁ A₂ = B₁ B₂ = C₁C₂ = C_τ

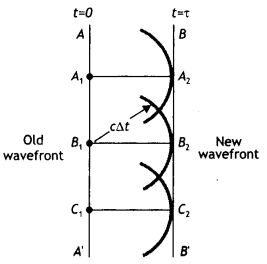
(b) A plane wavefront is incident on a convex lens. Explain, with the help of the diagram, the shape of the refracted wavefront formed. (CBSE AI 2019)
Answer:
Spherical wavefront

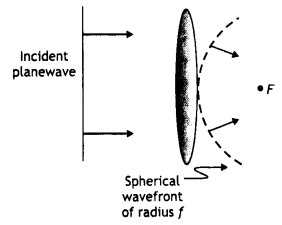
Question 42.
(a) In Young’s double-slit experiment, derive the condition for
(i) constructive Interference and
(ii) destructive Interference at a point on the screen.
Answer:
Consider a point P on the viewing screen; the screen is Located at a perpendicular distance D from the screen containing the slits S₁ and S₂, which are separated by a distance d as shown in the figure. Let us assume that the source of tight is monochromatic having a wavelength X. Under these conditions, the waves emerging from S and S have the same frequency and amplitude and are In phase.

If δ is the path difference between the waves from slits S₂ and S₁ at point P then
δ = r₂ – r₁ = d sin θ …(1)

where it is assumed that r₁ and r₂ are parallel, which is approximately true because D is much greater than d.

If this path difference is either zero or some Integral multiple of the wavelength, the waves are in phase at P and constructive Interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
δ = d sin θ = m λ …(2)

Here m is called the order number. In order to find the position of maxima measured vertically from O to P, i.e. y we assume that D >> d, that is, the distance from the slits to the screen is much larger than the distance between the two slits. (In practice D = 1 m and d = a few millimetre) Under these conditions, θ is small, and so the approximation sin θ ≈ tan θ. Therefore, from triangle POQ in the figure, we find that
sin θ = tan θ = \(\frac{Y}{D}\) …(3)

Substituting this in equation (2) we have
d \(\frac{Y}{D}\) = m λ …(2)

rewriting the above equation we have
y = \(\frac{mDλ}{d}\) …(4)
This gives the distance of the mth maxima from the centre 0 of the screen. For m = 0, 1, 2, 3, 4, ……. the values of y are
y_o = 0 …….. position of the central bright fringe

y₁ = \(\frac{Dλ}{d}\) ……. position of the first bright fringe

y₂ = \(\frac{2Dλ}{d}\) ……. position of the second bright fringe

y_m = \(\frac{mDλ}{d}\) …….position of the mth bright fringe

The spacing between any two bright fringes gives the width of a dark fringe. Therefore,

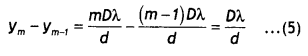
This gives the width of the dark fringe. Similarly, when the path difference is an odd multiple of λ/2, the waves arriving at P will be 180° out of phase and will give rise to destructive interference. There¬fore, the condition for dark fringes, or de¬structive interference, at P is given by

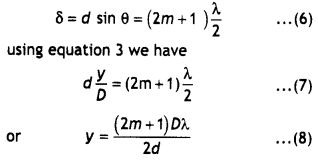
This gives the distance of the mth minima from the centre O of the screen. For m is equal to 0, 1, 2, 3, ……. we have
y’_o = \(\frac{Dλ}{2d}\), ……. position of the first dark fringe,

y’₁ = \(\frac{3Dλ}{2d}\) ……. position of the second dark fringe

y’₂ = \(\frac{5Dλ}{2d}\) ……. position of the third dark fringe and,

y’_m = \(\frac{(2 m+1) D \lambda}{2 d}\) ……. position of the mth dark fringe

Now the spacing between two consecutive dark fringes gives the width of the bright fringe, therefore, the width of the bright fringe is

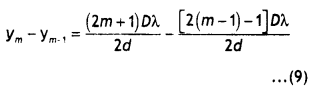
From equations 5 and 9 we find that the fringe width of the bright and the dark fringe is the same, therefore, the fringe width is given by
β = \(\frac{Dλ}{d}\) …(10)

(b) A beam of light consisting of two wavelengths, 800 nm and 600 nm, is used to obtain the interference fringes in Young’s double-slit experiment on a screen placed 1.4 m away. If the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide. (CBSE Al 2012)
Answer:
Let at a distance y from central maxima the bright fringes due to wavelengths l1 and l2 coincide first time. For this to happen, nl₁ = (n + 1)l₂, where n is an integer.
or
\(\frac{n+1}{n}=\frac{\lambda_{1}}{\lambda_{2}}=\frac{800 \times 10^{-9}}{600 \times 10^{-9}}=\frac{4}{3}\) solving for n we have n = 3

It means that at distance nth (3^th) maxima for wavelength λ₁ is just coinciding with (n + 1)^th (4^th) maxima for wavelength l₂

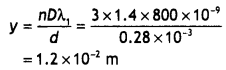
Question 43.
(a) How does an unpolarized light incident on a Polaroid get polarised? Describe briefly, with the help of a necessary diagram, the polarisation of light by reflection from a transparent medium.
(b) Two polaroids ‘A’ and ‘B’ are kept in a crossed position. How should a third Polaroid ‘C’ be placed between them so that the intensity of polarised light transmitted by Polaroid B reduces to 1/8th of the intensity of unpolarized light incident on A? (CBSE AI 2012)
Answer:
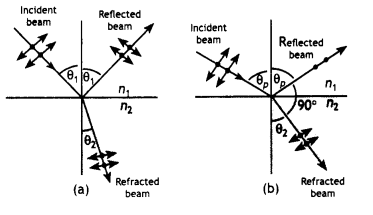
(a) The polariser allows only those vibrations of light to pass which are parallel to the pass axis of the polariser and blocks the remaining vibrations. Thus the light vibrations are restricted to only one plane.

Suppose an unpolarised light beam is an incident on a surface as shown in (figure a). The beam can be described by two electric field components, one parallel to the surface (the dots) and the other perpendicular to the first and to the direction of propagation (the arrows). It is found that the parallel components reflect more strongly than the other component, this results in a partially polarised beam. Furthermore, the refracted ray is also partially. polarised. Now suppose the angle of incidence 6, is varied until the angle between the reflected and the refracted beam is 90° (fig b). At this particular angle of incidence, the reflected beam is completely polarised with its electric vector parallel to the surface, while the refracted beam is partially polarised.

(b) Let l0 be the intensity of unpolarized light incident on Polaroid A. Then l_o/2 will be the intensity of polarised light after passing through the first polariser A. Then the intensity of light after passing through second polariser B will be l = (l_o/2)cos²θ

where θ is the angle between pass axes of A and B. Since A and B are crossed the angle between the pass axes of B and C will be (π/2 – θ). Hence the intensity of light emerging from C will be

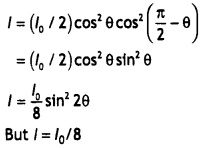
Therefore, we have
\(\frac{l_{0}}{8}=\frac{l_{0}}{8}\) sin² 2θ or sin 2θ = 1 or 2θ = 90°
i.e. θ = π/4

Therefore, the transmitted intensity will be maximum when θ = π/4

Question 44.
(a) Describe any two characteristic features which distinguish between interference and diffraction phenomena. Derive the expression for the intensity at a point of the interference pattern in Young’s double-slit experiment.
(b) In the diffraction due to a single slit experiment, the aperture of the slit is 3 mm. If monochromatic light of wavelength 620 nm is incident normally on the slit, calculate the separation between the first order minima and the 3^rd order maxima on one side of the screen. The distance between the slit and the screen is 1.5 m. (CBSE Delhi 2019)
Answer:
(a) (i) Interference pattern has a number of equally spaced bright and dark bands, while the diffraction pattern has a central bright maximum which is twice as wide as the other maxima.

(ii) In interference pattern, the intensity of all bright fringes is the same, while in diffraction pattern intensity of bright fringes goes on decreasing with the increasing order of the maxima.

Let the displacements of the waves from the sources S₁ and S₂ at a point P on the screen at any time t be given by y₁ = a cos cot and y₂ = a cos (ωt + Φ), where Φ is the constant phase difference between the two waves.

By the superposition principle, the resultant displacement at point P is given by

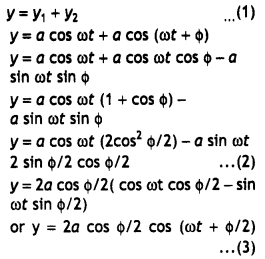
Thus the amplitude of the resultant displacement is
A = 2a cos (Φ/2) …(4)

Therefore the intensity at that point is
l = A² = 4a² cos²\(\frac{Φ}{2}\) …(5)

(b) Given a = 3mm = 3 × 10^-3m, λ = 620nm = 620 × 10^-9 m, D = 1.5 m Distance of first-order minima from centre of the central maxima = X_D1 = λ_D/a

Distance of third order maxima from centre of the central maxima X_D3 = 7λ_D/2a

Distance between first order minima and third order maxima = X_D3 – X_D1

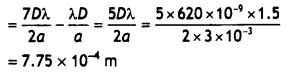
Question 45.
(a) In Young’s double-slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence deduce the expression for the fringe width.
Answer:
Consider a point P on the viewing screen; the screen is Located at a perpendicular distance D from the screen containing the slits S_D1 and S₂, which are separated by a distance d as shown in the figure. Let us assume that the source of tight is monochromatic having a waveLength X. Under these conditions, the waves emerging from S and S have the same frequency and amplitude and are In phase.

If δ is the path difference between the waves from slits S2 and S1 at point P then
δ = r₂ – r₁ = d sin θ …(1)

where it is assumed that r1 and r2 are parallel, which is approximately true because D is much greater than d.

If this path difference is either zero or some Integral multiple of the wavelength, the waves are in phase at P and constructive Interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
δ = d sin θ = m λ …(2)

Here m is called the order number. In order to find the position of maxima measured vertically from O to P, i.e. y we assume that D >> d, that is, the distance from the slits to the screen is much larger than the distance between the two slits. (In practice D = 1 m and d = a few millimetre) Under these conditions, θ is small, and so the approximation sin θ ≈ tan θ. Therefore, from triangle POQ in the figure, we find that
sin θ = tan θ = \(\frac{Y}{D}\) …(3)

Substituting this in equation (2) we have
d \(\frac{Y}{D}\) = m λ …(2)

rewriting the above equation we have
y = \(\frac{mDλ}{d}\) …(4)
This gives the distance of the mth maxima from the centre 0 of the screen. For m = 0, 1, 2, 3, 4, ……. the values of y are
y_o = 0 …….. position of the central bright fringe

y₁ = \(\frac{Dλ}{d}\) ……. position of the first bright fringe

y₂ = \(\frac{2Dλ}{d}\) ……. position of the second bright fringe

y_m = \(\frac{mDλ}{d}\) …….position of the mth bright fringe

The spacing between any two bright fringes gives the width of a dark fringe. Therefore,

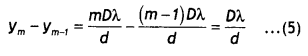
This gives the width of the dark fringe. Similarly, when the path difference is an odd multiple of λ/2, the waves arriving at P will be 180° out of phase and will give rise to destructive interference. Therefore, the condition for dark fringes, or destructive interference, at P is given by

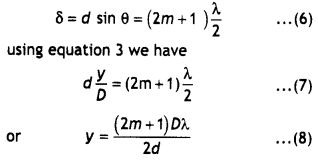
This gives the distance of the mth minima from the centre O of the screen. For m is equal to 0, 1, 2, 3, ……. we have
y’_o = \(\frac{Dλ}{2d}\), ……. position of the first dark fringe,

y’₁ = \(\frac{3Dλ}{2d}\) ……. position of the second dark fringe

y’₂ = \(\frac{5Dλ}{2d}\) ……. position of the third dark fringe and,

y’_m = \(\frac{(2 m+1) D \lambda}{2 d}\) ……. position of the mth dark fringe

Now the spacing between two consecutive dark fringes gives the width of the bright fringe, therefore, the width of the bright fringe is

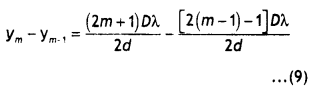
From equations 5 and 9 we find that the fringe width of the bright and the dark fringe is the same, therefore, the fringe width is given by
β = \(\frac{Dλ}{d}\) …(10)

(b) Show that the fringe pattern on the screen is actually a superposition of single-slit diffraction from each slit.
Answer:
It is a broader diffraction peak in which there appear several fringes of smaller width due to the double-slit interference pattern. This is shown below:

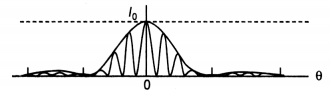
(c) What should be the width of each slit to obtain 10 maxima of the double-slit pattern within the central maximum of the single-slit pattern, for the green light of wavelength 500 nm, if the separation between two slits is 1 mm? (CBSE AI 2015)
Answer:
Given 10 b = width of central maxima in diffraction pattern λ = 500 nm, d= 1 mm,
Now 10\(\frac{Dλ}{d}\) = \(\frac{Dλ}{a}\)
or
a = \(\frac{d}{5}=\frac{1}{5}\) = 0.2 mm

Question 46.
(a) Define a wavefront. How is it different from a ray?
Answer:
A wavefront is defined as the locus of all adjacent points at which the phase of vibration of a physical quantity associated with the wave is the same.

It is in two dimensions while a ray is in one dimension.

(b) Depict the shape of a wavefront in each of the following cases.
(i) Light diverging from a point source,
Answer:

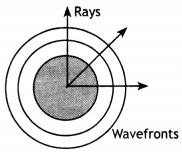
(ii) Light emerging out of a convex lens when a point source is placed at its focus.
Answer:

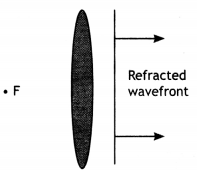
(c) Using Huygen’s construction of secondary wavelets, draw a diagram showing the passage of a plane wavefront from a denser into a rarer medium. (CBSE AI 2015C)
Answer:
The diagram is as shown

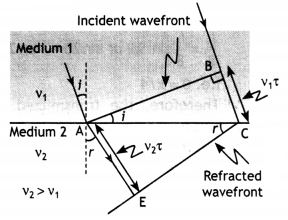
Question 47.
(a) Why does unpolarised light from a source show a variation in intensity when viewed through a Polaroid which is rotated? Show with the help of a diagram how unpolarised light from sun got linearly polarised by scattering.
(b) Three identical Polaroid sheets P1, P2 and P3 are oriented so that the pass axis of P2 and P3 are inclined at angles of 60° and 90° respectively with the pass axis of P1. A monochromatic source S of unpolarised light of intensity l0 is kept in front of the polaroid sheet P! as shown in the figure. Determine the intensities of light as observed by the observer at O when Polaroid P3 is rotated with respect to P2 at angles θ = 30° and 60°. (CBSE AI 2016)

Answer:
(a) When light passes through a Polaroid it absorbs all vibrations which are not parallel to its pass axis.
It is found that when unpolarised sunlight is incident on a small dust particle or air molecules it is scattered in all directions. The light scattered in a direction perpendicular to the incident light is found to be completely polarised.

The electric vector of incident light has components both in the plane of the paper as well as perpendicular to the plane of the paper. The electrons under the influence of the electric vector acquire motion in both directions. However, radiation scattered by the molecules in perpendicular direction contains only components represented by dots (.), i.e. polarised perpendicular to the plane of the paper.

(b) Let l0 be the intensity of light before passing P₁ Intensity of light coming out of P₁ will be l_o/2.

Then the intensity of light after passing through second poloroid (analyser) is
l₂ = \(\frac{l_{0}}{2}\)cos²60° = \(\frac{l_{0}}{8}\)

When P₃ is rotated with respect to P₂ at an angle of 30°, then angle be¬tween the pass axis of P₂ and P₃ will be θ = 30°+ 30° = 60°.
Hence l3 = l2 cos²60° = \(\frac{l_{0}}{8} \times \frac{1}{4}=\frac{l_{0}}{32}\)
or
θ = 30° – 30° = 0°

Therefore, l₃ = l₂ cos² 0° = l₂ = l_o/8
When P₃ is rotated with respect to P₂ at an angle of 60°, then the angle between the pass axis of P₂ and P₃ will be
θ = 30° + 60° = 90°

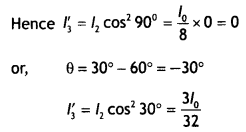
Question 48.
(a) Derive an expression for path difference in Young’s double-slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
Answer:
Consider a point P on the viewing screen; the screen is Located at a perpendicular distance D from the screen containing the slits S₁ and S₂, which are separated by a distance d as shown in the figure. Let us assume that the source of tight is monochromatic having a waveLength X. Under these conditions, the waves emerging from S and S have the same frequency and amplitude and are In phase.

If δ is the path difference between the waves from slits S₂ and S₁ at point P then
δ = r₂ – r₁ = d sin θ …(1)

where it is assumed that r₁ and r₂ are parallel, which is approximately true because D is much greater than d.

If this path difference is either zero or some Integral multiple of the wavelength, the waves are in phase at P and constructive Interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
δ = d sin θ = m λ …(2)

Here m is called the order number. In order to find the position of maxima measured vertically from O to P, i.e. y we assume that D >> d, that is, the distance from the slits to the screen is much larger than the distance between the two slits. (In practice D = 1 m and d = a few millimetre) Under these conditions, θ is small, and so the approximation sin θ ≈ tan θ. Therefore, from triangle POQ in the figure, we find that
sin θ = tan θ = \(\frac{Y}{D}\) …(3)

Substituting this in equation (2) we have
d \(\frac{Y}{D}\) = m λ …(2)

rewriting the above equation we have
y = \(\frac{mDλ}{d}\) …(4)
This gives the distance of the mth maxima from the centre 0 of the screen. For m = 0, 1, 2, 3, 4, ……. the values of y are
y_o = 0 …….. position of the central bright fringe

y₁ = \(\frac{Dλ}{d}\) ……. position of the first bright fringe

y₂ = \(\frac{2Dλ}{d}\) ……. position of the second bright fringe

y_m = \(\frac{mDλ}{d}\) …….position of the mth bright fringe

The spacing between any two bright fringes gives the width of a dark fringe. Therefore,

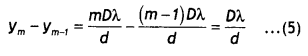
This gives the width of the dark fringe. Similarly, when the path difference is an odd multiple of λ/2, the waves arriving at P will be 180° out of phase and will give rise to destructive interference. There¬fore, the condition for dark fringes, or de¬structive interference, at P is given by

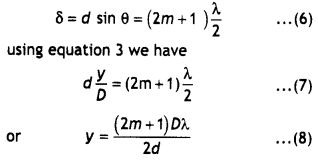
This gives the distance of the mth minima from the centre O of the screen. For m is equal to 0, 1, 2, 3, ……. we have
y’_o = \(\frac{Dλ}{2d}\), ……. position of the first dark fringe,
y’₁ = \(\frac{3Dλ}{2d}\) ……. position of the second dark fringe
y’₂ = \(\frac{5Dλ}{2d}\) ……. position of the third dark fringe and,
y’_m = \(\frac{(2 m+1) D \lambda}{2 d}\) ……. position of the mth dark fringe

Now the spacing between two consecutive dark fringes gives the width of the bright fringe, therefore, the width of the bright fringe is

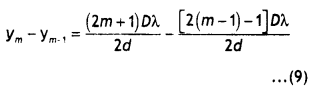
From equations 5 and 9 we find that the fringe width of the bright and the dark fringe is the same, therefore, the fringe width is given by
β = \(\frac{Dλ}{d}\) …(10)

(b) The Intensity at the central maxima in Young’s double-slit experiment is l0. Find out the intensity at a point where the path difference is λ/6, λ/4 and λ/3. (CBSE AI 2016)
Answer:
Let l be the intensity of light coming out of each slit. Since waves at the central maxima are in phase, therefore, we have

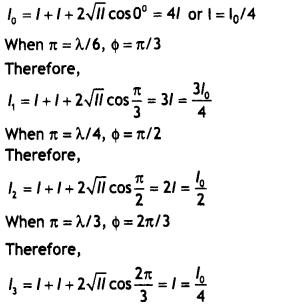
Question 49.
(a) Define a wavefront. Using Huygens’ Principle, verify the laws of reflection at a plane surface.
Answer:
The wavefront is a locus of points that oscillate in the same phase.

Consider a plane wavefront AB incident obliquely on a plane reflecting surface MM^–. Let us consider the situation when one end A of wavefront strikes the mirror at an angle i but the other end B has still to cover distance BC. The time required for this will be t = BC/c.

According to Huygen’s principle, point A starts emitting secondary wavelets and in time t, these will cover a distance c t = BC and spread. Hence, with point A as centre and BC as radius, draw a circular arc. Draw tangent CD on this arc from point C. Obviously, the CD is the reflected wavefront inclined at an angle ‘r’. As incident wavefront and reflected wavefront, both are in the plane of the paper, the 1^st law of reflection is proved.

To prove the second law of reflection, consider ΔABC and ΔADC. BC = AD (by construction),
∠ABC = ∠ADC = 90° and AC is common.

Therefore, the two triangles are congruent and, hence, ∠BAC = ∠DCA or ∠i = ∠r, i.e.the angle of reflection is equal to the angle of incidence, which is the second law of reflection.
Or
The refractive index of medium 2, w.r.t. medium 1 equals the ratio of the sine of the angle of incidence (in medium 1) to the sine of the angle of refraction (in medium 2), The diagram is as shown.

From the diagram

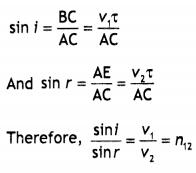
(b) In a single-slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band? Explain.
Answer:
Size of central maxima reduces to half, (Size of central maxima = 2λD/d) Intensity increases.
This is because the amount of light, entering the slit, has increased and the area, over which it falls, decreases.

(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the obstacle. Explain why. (CBSE AI 2018, Delhi 2018)
Answer:
This is because of the diffraction of light. Light gets diffracted by the tiny circular obstacle and reaches the centre of the shadow of the obstacle.
β = \(\frac{Dλ}{d}\).

(i) When D is decreased, the fringe width decreases.
(ii) When d is Increased, the fringe width decreases.

Question 50.
The following figure shows an experiment set up similar to Young’s double-slit experiment to observe interference of light.

Here SS₂ – SS₁ = λ/4
Write the condition of (i) constructive,
(ii) destructive Interference at any point P in terms of path difference Δ = S₂P – S₁P.

Does the central fringe observed in the above set up tie above or below O? Give reason in support of your answer.
Yellow light of wavelength 6000°A produces fringes of width 08 mm in Young’s double-slit experiment. What will be the fringe width if the light source is replaced by another monochromatic source of wavelength 7500° A and separation between the slits is doubled?
Answer:
Given SS₂ – SS₁ = λ/4
Now path difference between the two waves from slits S₁ and S₂ on reaching point P on screen is

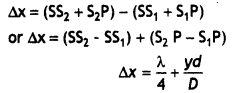
(a) For constructive interference at point P both difference Δx = nλ.
Therefore

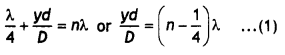
where n = 0, 1, 2, 3, …

(b) For destructive interference at point P path difference

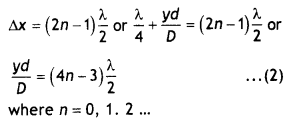
For central bright fringe, putting n = 0 in equation (1), we get
\(\frac{y d}{D}=-\frac{\lambda}{4}\)
or
y = – \(\frac{\lambda D}{4 d}\)

The -ve sign indicates that the central bright fringe will be observed below centre O of the screen, at distance below it.
Given λ₁ = 6000°A, β₁ = 0.8 mm,
λ₂ = 7500°A, β₂ = ?, d₂ = 2d₁

Using the expression
β = \(\frac{Dλ}{d}\) we have
\(\frac{\beta_{2}}{\beta_{1}}=\frac{\lambda_{2} d_{1}}{\lambda_{1} d_{2}}=\frac{7500}{6000} \times \frac{d_{1}}{2 d_{1}}\)

Solving we have β₂ = 0.5 mm

Question 51.
(a) There are two sets of apparatus of Young’s double-slit experiment. Inset A, the phase difference between the two waves emanating from the slits does not change with time, whereas in set B, the phase difference between the two waves from the slits changes rapidly with time. What difference will be observed in the pattern obtained on the screen in the two setups?
(b) Deduce the expression for the resultant intensity in both the above- mentioned setups (A and B), assuming that the waves emanating from the two slits have the same amplitude A and same wavelength λ.
Or
(a) The two polaroids, in a given setup, are kept ‘crossed’ with respect to each other. A third polaroid, now put in between these two polaroids, can be rotated. Find an expression for the dependence of the intensity of light I, transmitted by the system, on the angle between the pass axis of the first and the third polaroid. Draw a graph showing the dependence of l on θ.
(b) When an unpolarized light is an incident on a plane glass surface, find the expression for the angle of incidence so that the reflected and refracted light rays are perpendicular to each other. What is the state of polarization, of reflected and refracted light, under this condition?
Answer:
(a) Set A: Stable interference pattern, the positions of maxima and minima, does not change with time.
Set B: Positions of maxima and minima will change rapidly with time and an average uniform intensity distribution will be observed on the screen.

(b) Let the displacements of the waves from the sources S1 and S2 at a point on the screen at any time t be given by y₁ = a cos ωt and y₂ = a cos (ωt + Φ), where Φ is the constant phase difference between the two waves. By the superposition principle, the resultant displacement at point P is given by

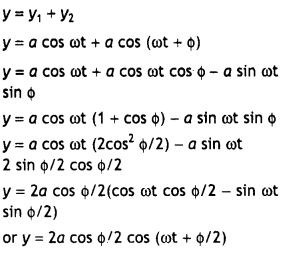
Thus the amplitude of the resultant displacement is A = 2a cos (Φ/2)

Therefore, the intensity at that point is l = A² = 4a² cos²\(\frac{Φ}{2}\) – 4l_o cos²\(\frac{Φ}{2}\)
Since Φ = 0, l.e. there is no phase difference, hence l = 4 l_o

Inset B, the intensity will be given by the average intensity
l = 4l_o\(\left(\cos ^{2} \frac{\phi}{2}\right)\) = 2l_o
Or
(a) Let P₁ and P₂ be the two crossed Polaroids and P₃ be the polaroid kept between the two. Let l_o, be the intensity of polarised light after passing through the first Polaroid P₁. Then the Intensity of light after passing through the second Polaroid P₂ will be,
l = l_o cos² θ
where θ is the angle between pass axes of P₁ and P₂. Since P₁ and P₂ are crossed the angle between the pass axes of P₂ and P₃ will be (π/2 – 0). Hence the intensity of light emerging from P2₂ will be

The transmitted intensity will be maximum when π = π/4. The graph is as shown

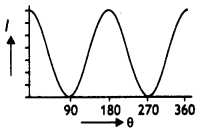
(b) The ray diagram is as shown.

When light Is incident at a certain angle called Brewster angle, the reflected beam is completely polarised with its electric vector parallel to the surface, while the refracted beam is partially polarised. The angle of incidence at which this occurs is called the polarising angle i_B.

From figure we see that at the polaris-ing angle
i_B + 90° + r = 180°
or
r = 90° – i_B.

Using Snell’s law we have
μ = \(\frac{\sin i_{\mathrm{B}}}{\sin r}\)

Now sin r = (90° – i_B), therefore the above expression becomes

Nature of polarisation: Reflected light and linearly polarised

Numerical Problems:
Formulae for solving numerical problems

• Fringe width is given by β = \(\frac{Dλ}{d}\)
• Brewster’s Law: μ = \(\frac{\sin \theta_{p}}{\cos \theta_{p}}\) = tan θ_p
• Intensity of light coming out of a polariser l = l_o cos² θ
• If l₁ and l₂ are the intensities of light emitted by the two sources, w₁ and w₂ be the widths of the two slits, a₁ and a₂ be the amplitudes of the waves from the two slits then,
  \(\frac{l_{1}}{l_{2}}=\frac{w_{1}}{w_{2}}=\frac{a_{1}^{2}}{a_{2}^{2}}\)
• lf l_max and lmin be the intensities of light at the maxima and the minima the
  \(\frac{l_{\max }}{l_{\min }}=\frac{\left(a_{1}+a_{2}\right)^{2}}{\left(a_{1}-a_{2}\right)^{2}}\)

Question 1.
Laser light of wavelength 630 nm incident on a pair of slits produces an interference pattern in which the bright fringes are separated by 7.2 mm. Calculate the wavelength of another source of laser light that produces interference fringes separated by 8.1 mm using the same pair of slits. (CBSE Al 2011C)
Answer:
Given λ₁ = 630 nm, β₁ = 7.2 mm, β₂ = 8.1 mm, λ₂ =?

We know that β = \(\frac{Dλ}{d}\), for the same value of D and d we have β₂ ∝ λ,
Therefore, we have

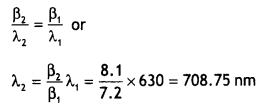
Question 2.
What is the speed of light in a denser medium of polarising angle 30°? (CBSE Delhi 2019)
Answer:

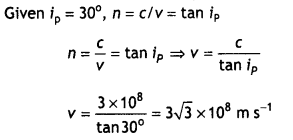
Question 3.
Laser light of wavelength 640 nm incident on a pair of slits produces an interference pattern in which the bright fringes are separated by 7.2 mm. Calculate the wavelength of another source of light that produces interference fringes separated by 8.1 mm using the same arrangement. Also, find the minimum value of the order (n) of the bright fringe of the shorter wavelength which coincides with that of the longer wavelength. (CBSE AI 2012C)
Answer:
Given λ₁ = 640 nm, λ₂ = ?, b₁ = 7.2 mm and b₂ = 8.1 mm

Using the expression β = \(\frac{Dλ}{a}\) we have

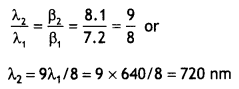
Now n fringes of shorter wavelength will coincide with (n – 1) fringes of Longer wavelength
n₁λ₁ = n₂λ₂
or
n × 640 = (n – 1) × 720
Solving for n we have n =9

Question 4.
Yellow light (λ = 6000 Å) illuminates a single-slit of width 1 × 10 m. Calculate
(a) the distance between the two dark tines on either side of the central maximum, when the diffraction pattern is viewed on a screen kept 1.5 m away from the slit;
(b) the angular spread of the first diffraction minimum. (CBSE AI 2012C)
Answer:

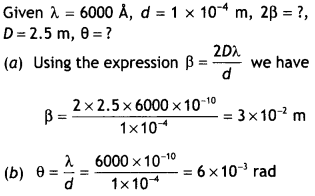
Question 5.
Find the ratio of Intensities of two points P and Q on the screen in Young’s double-slit experiment when the waves from sources S₁ and S₂ have a phase difference of (i) π/3 and (11) π/2.
Answer:
Intensity at the screen when the phase difference is Φ = π/3 is

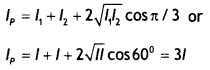
Now intensity at the screen when the phase difference is Φ = 90° is

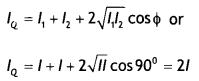
Therefore, ratio of intensities is
\(\frac{l_{p}}{l_{Q}}=\frac{3l}{2l}=\frac{3}{2}\)

Question 6.
In young’s double-slit experiment, two sifts are separated by 3 mm distance and illuminated by the light of wavelength 480 nm. The screen is at 2 m from the plane of the slits. Calculate the separation between the 8th bright fringe and the 3N dark fringes observed with respect to the central bright fringe.
Answer:
Using the formuLa

Question 7.
Two coherent sources have Intensities In the ratio 25: 16. Find the ratio of the Intensities of maxima to minima, after the interference of light occurs.
Answer:
In the given problem

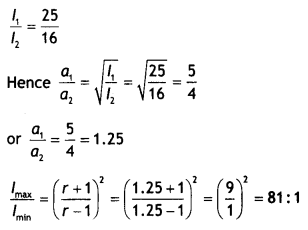
Question 8.
The ratio of intensities of maxima and minima in an interference pattern is found to be 25: 9. Calculate the ratio of light intensities of the sources producing this pattern.
Answer:
Given

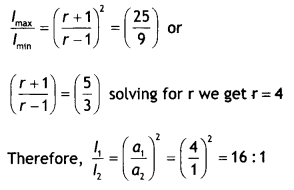
Question 9.
In Young’s double-slit experiment using the light of wavelength 400 nm, Interference fringes of width X are obtained. Th. the wavelength of light is Increased to 600 nm and the separation between the slits Is halved. If on. wants the observed fringe width on the screen to b. the same in the two cases, find the ratio of the distance between the screen and the plan. of the Interfering sources In the two arrangements.
Answer:
Let D₁ be the distance between the screen and the sources when a tight of wavelength 400 nm Is used.

β = \(\frac{Dλ}{a}\)
or
X = \(\frac{D_{1} \times 400 \times 10^{-9}}{d}\) …(i)

Let D₂ be the distance between the screen and the sources to obtain the same fringe width, when light of wavelength 600 nm is used. Then,
X = \(\frac{D_{2} \times 600 \times 10^{-9}}{d}\) ….(ii)

From the equations (i) and (ii), we have
\(\frac{D_{1}}{D_{2}}=\frac{600 \times 10^{-9}}{400 \times 10^{-9}}\) = 1.5

Question 10.
In Young’s slit experiment, Interference fringes are observed on a screen, kept at D from the slits. If the screen Is moved towards the slits by 5 × 10^-2 m, the change in fringe width Is found to be 3 × 10^-5 m. If the separation between the slits is 10-3 m, calculate the wavelength of the light used.
Answer:
Given ΔD = 5 × 10^-2-2 m, Δβ = 3 × 10^-5-5 m, d = 10^-3 m,

Using the relation β = \(\frac{Dλ}{a}\) we have for the two cases
β₁ = \(\frac{D_{1} \lambda}{d}\) and
β₂ = \(\frac{D_{2} \lambda}{d}\) subtracting we have
β₁ – β₂ = \(\frac{λ}{d}\)(D1 – D2)
or

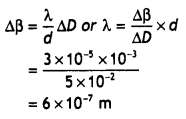
Question 11.
A slit of width ‘a’ is illuminated by monochromatic light of wavelength 700 nm at Normal Incidence. Calculate the value of ‘a’ for the position of
(a) the first minimum at an angle of diffraction of 30°.
(b) first maximum at an angle of diffraction of 30°.
Answer:
Given X = 700 nm = 7 × 10^-7 m

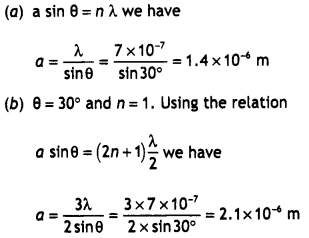
Question 12.
Estimate the angular separation between . first order maximum and third order minimum of the diffraction pattern due to a single-slit of width 1 mm, when light of wavelength 600 nm is incident normal on it. (CBSE AI 2015C)
Answer:
Given d = 1 mm = 10^-3 m,
λ = 600 nm = 6 × 10^-7 m,
For first order maxima
d sin θ = n λ
or
sin θ = \(\frac{n \lambda}{d}=\frac{6 \times 10^{-7}}{10^{-3}}\) = 6 × 10^-4
or
θ_max = 1.047°
Now for minima we have
d sin θ = (2n+1 )\(\frac{λ}{2}\)

For third-order minima we have n = 3
Therefore we have

sin θ = (2 × 3 + 1)\(\frac{λ}{2d}\) = \(\frac{7λ}{2d}\)
= \(\frac{7 \times 6 \times 10^{-7}}{2 \times 10^{-3}}\)
= 21 × 10^-4
or
θ_min = 6.397°

Therefore, angular separation is
θ_min – θ_max = 6.397 – 1.047 = 5.35°