Electrostatic Potential and Capacitance Class 12 Important Extra Questions Physics Chapter 2

Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 2 Electrostatic Potential and Capacitance. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.

Class 12 Physics Chapter 2 Important Extra Questions Electrostatic Potential and Capacitance

Electrostatic Potential and Capacitance Important Extra Questions Very Short Answer Type

Question 1.
Express dielectric constant in terms of the capacitance of a capacitor.
Answer:
It is given by the expression K = \(\frac{c}{c_{0}}\) where C is the capacitance of the capacitor with dielectric and C₀ is the capacitance without the dielectric.

Question 2.
On what factors does the capacitance of a parallel plate capacitor depend?
Answer:

1. Area of plates,
2. The separation between the plates and
3. Nature of dielectric medium between the plates.

Question 3.
What is the ratio of electric field intensities at any two points between the plates of a capacitor?
Answer:
The ratio is one, as the electric field is the same at all points between the plates of a capacitor.

Question 4.
Write a relation between electric displacement vector D and electric field E.
Answer:
\(\vec{D}\) = ε₀ \(\vec{E}\) + \(\vec{P}\)

Question 5.
Write the relation between dielectric constant (K) and electric susceptibility χ_e
Answer:
K = 1 + χ_e

Question 6.
A hollow metal sphere c radius 5 cm is charged such that the potential on its surface is 10 V. What is the potential at the center of the sphere? (CDSE AI 2011)
Answer:
10 V

Question 7.
What is the geometrical shape of equipotential surfaces due to a single isolated charge? (CBSE Delhi 2013)
Answer:
Concentric circles.

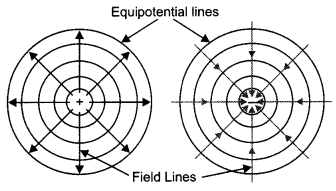
Question 8.
Draw the equipotential surfaces due to an isolated point charge. (CBSE Delhi 2019)
Answer:
These areas are shown.

Question 9.
‘For any charge configuration, equipotential surface through a point is normal to the electric field’. Justify. (CBSE Delhi 2014)
Answer:
This is because work done in moving a charge on an equipotential surface is zero. This is possible only if the equipotential surface is perpendicular to the electric field.

Question 10.
The given graph shows the variation of charge ‘q’ versus potential difference ‘V for two capacitors C₁ and C₂. Both the capacitors have the same plate separation but the plate area of C₂ is greater than that of C_y Which line (A or B) corresponds to C₁ and why? (CBSEAI 2014C)

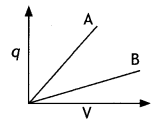
Answer:
Since C = ε₀ A/d, since the area for C₂ is more, therefore capacitance of C₂ is more. From the graph greater the slope greater is than the capacitance, therefore, graph A belongs to capacitor C₂. While graph B belongs to capacitance C_v

Question 11.
Write a relation for polarisation P of dielectric material in the presence of an external electric field E . (CBSE AI 2015)
Answer:
P = χ_e ε₀ \(\vec{E}\).

Question 12.
Why are electric field lines perpendicular at a point on an equipotential surface of a conductor? (CBSE AI 2015C)
Answer:
So that no net force acts on the charge on the equipotential surface and it remains stationary.

Question 13.
Why does a given capacitor store more charge at a given potential difference when a dielectric is filled in between the plates?
Answer:
Because the capacitance of the capacitor increases on filling the dielectric medium in between the plates.

Question 14.
Why is the electrostatic potential inside a charged conducting shell constant throughout the volume of the conductor? (CBSE AI 2019)
Answer:
We know that E = – \(\frac{d V}{d r}\)
Inside a conductor, the electric field is zero and no work is done in moving a charge inside a conductor. Therefore, V is constant.

Question 15.
Does the charge given to a metallic sphere depend on whether it is hollow or solid? (CBSE Delhi 2017)
Answer:
If the capacitance of the two spheres, solid and hollow, is the same, then they will hold the same quantity of charge.

Question 16.
Is the electric potential necessarily zero at a place where the electric field is zero?
Answer:
No, it is not necessary. The electric field inside a hollow metallic conductor is zero but the electric potential is not zero.

Question 17.
In a parallel plate capacitor, the potential difference of 10² V is maintained between the plates. What will be the electric field at points A and B as shown in the figure below?
Answer:
The electric field between the plates of a capacitor is uniform; therefore the electric field at points A and B will be the same.

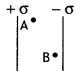
Question 18.
If the plates of a charged capacitor are suddenly connected to each other by a wire, what will happen?
Answer:
The capacitor is discharged immediately.

Question 19.
Can you place a parallel plate capacitor of one farad capacity in your house?
Answer:
Ordinarily, it is not possible because the surface area of such a capacitor will be extra-large.

Question 20.
Is there any conductor which can be given almost unlimited charge?
Answer:
Yes, the earth.

Question 21.
What would be the work done if a point charge + q is taken from a point A to a point B on the circumference of a circle drawn with another point charge + q at the center?

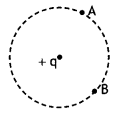
Answer:
Zero.

Question 22.
Sketch a graph to show how a charge Q, acquired by a capacitor of capacitance, C, varies with the increase in the potential difference between the plates.
Answer:

Question 23.
In a parallel plate capacitor, the capacitance increases from 4 μF to 80 μF, introducing a dielectric medium between the plates. What is the dielectric constant of the medium?
Answer:
The dielectric constant is given by
K = \(\frac{80}{4}\) = 20

Electrostatic Potential and Capacitance Important Extra Questions Short Answer Type

Question 1.
Draw a plot showing the variation of (i) electric field (E) and (ii) electric potential (V) with distance r due to a point charge Q. (CBSE Delhi 2012)
Answer:
The plot is as shown.

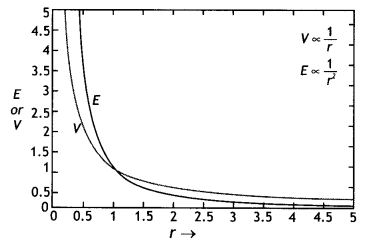
Question 2.
Two identical capacitors of 10 pF each are connected in turn (i) in series and (ii) in parallel across a 20 V battery. Calculate the potential difference across each capacitor in the first case and the charge acquired by each capacitor in the second case. (CBSE AI 2019)
Answer:
(i) Since the two capacitors have the same capacitance, therefore, the potential will be divided amongst them. Hence V = 10 V each
(ii) Since the capacitors are connected in parallel, therefore, potential difference = 20 V
Hence charge Q = CV = 10 × 20 = 200 pC

Question 3.
A point charge ‘q’ is placed at O as shown in the figure. Is V_A – V_B positive, negative, or zero, if ‘q’ is an (i) positive, (ii) negative charge? (CBSE Delhi 2011, 2016)

Answer:
If V_A – V_B = \(\frac{q}{4 \pi \varepsilon_{0}}\left(\frac{1}{\mathrm{OA}}-\frac{1}{\mathrm{OB}}\right)\)

As OA < OB
∴ If q is positive then V_A– V_B is positive and
if q is negative V_A – V_B is also negative.

Question 4.
The graph shows the variation of voltage V across the plates of two capacitors A and B versus charge Q stored on them. Which of the two capacitors has higher capacitance? Give a reason for your answer.

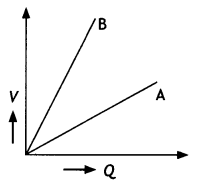
Answer:
Capacitor A has higher capacitance. We know that capacitance C = Q/V.

For capacitor A
\(c_{A}=\frac{Q}{V_{A}}\)

For capacitor B
\(c_{B}=\frac{Q}{V_{B}}\)

As V_B > V_A
∴ C_B < C_A
Thus capacitance of A is higher.

Question 5.
A test charge ‘q’ is moved without acceleration from A to C along the path from A to B and then from B to C in electric field E as shown in the figure,

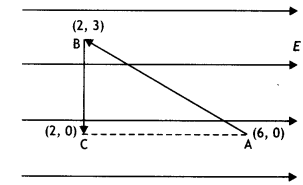
(i) Calculate the potential difference between A and C
Answer:
(i) dV = – E dr = – E (6 – 2) = – 4E

(ii) At which point (of the two) is the electric potential more and why? (CBSE AI 2012)
Answer:
Electric potential is more at point C as dV = – Edr, i.e. the electric potential decreases in the direction of the electric field.

Question 6.
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/2, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor. (CBSE AI 2013)
Answer:
Given t = d/2, C = ?
We know that when a dielectric of thickness ‘t’ is inserted between the plates of a capacitor, its capacitance is given by
C = \(\frac{\varepsilon_{0} A}{d-t+\frac{t}{K}}\)

Hence we have
C = \(\frac{\varepsilon_{0} A}{d-\frac{d}{2}+\frac{d}{2 K}}=\frac{2 K \varepsilon_{0} A}{d(1+K)}\)

Question 7.
Two-point charges q and -2q are kept ‘d’ distance apart. Find the location of the point relative to charge ‘q’ at which potential due to this system of charges is zero. (CBSE Al 2014C)
Answer:
Let the potential be zero at point P at a distance x from charge q as shown

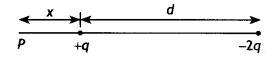
Now potential at point P is
V = \(\frac{k q}{x}+\frac{k(-2 q)}{d+x}\) = 0

Solving for x we have
x = d

Question 8.
Four-point charges Q, q, Q., and q are placed at the corners of a square of side ‘a’ as shown in the figure.

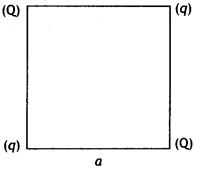
Find the potential energy of this system. (CBSEAI, Delhi 2018)
Answer:
The potential energy of the system
U = \(\frac{1}{4 \pi \varepsilon_{0}}\left(4 \frac{q Q}{a}+\frac{q^{2}}{a \sqrt{2}}+\frac{Q^{2}}{a \sqrt{2}}\right)\)

U = \(\frac{1}{4 \pi \varepsilon_{0} a}\left(4 q Q+\frac{q^{2}}{\sqrt{2}}+\frac{Q^{2}}{\sqrt{2}}\right)\)

Question 9.
Three-point charges q, -4q, and 2q are placed at the vertices of an equilateral triangle ABC of side T as shown in the figure. (CBSE Delhi 2018)

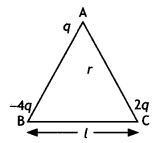
Find out the amount of the work done to separate the charges at infinite distance. (CBSE AI, Delhi 2018)
Answer:
Net potential energy of the system
= \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q^{2}}{l}[-4+2-8]=\frac{5 q^{2}}{2 \pi \varepsilon_{0} l}\)

Electrostatic Potential and Capacitance Important Extra Questions Long Answer Type

Question 1.
Two-point charges 2 μC and —2 μC are placed at points A and B 6 cm apart.
(a) Draw the equipotential surfaces of the system.
Answer:
The diagram is as shown.

(b) Why do the equipotential surfaces get closer to each other near the point charges? (CBSEAI2O11C)
Answer:
We know that E = – dV/dr
Therefore, dr =- dV/E
Since near the charge, electric field E is large, dr will be less.

Question 2.
(a) Obtain the expressions for the resultant capacitance when the three capacitors C₁, C_2, and C₃ are connected (i) in parallel and then (ii) in series.
Answer:
(i) Parallel combination of three capacitors.
Let three capacitors of capacitances C₁, C₂, and C₃ be connected in parallel, and potential difference V be applied across A and B. If q be total charge flowing in the circuit and q₁ q₂ and q₃ be charged flowing across C₁, C_2, and C₃ respectively, then
q = q₁+ q₂ + q₃
or q = C₁v + C₂V + C₃V …(i)

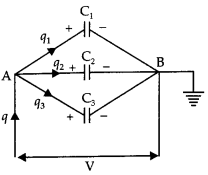
If C_P is the capacitance of the arrangement in parallel, then
q = C_PV

So equation (i) becomes
C_PV = C₁V + C₂V + C₃V
Or
C_P = C₁ + C₂ + C₃

(ii) Series combination of three capacitors Let three capacitors C₁, C₂, and C₃ be connected in series. Let q charge be flowing through the circuit.
If V₁, V₂, and V₃ be potential differences across the plates of the capacitor and V be the potential difference across the series combination, then

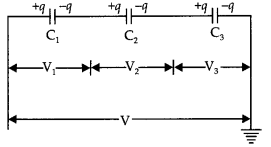
V = V₁ + V₂ + V₃
Or
V = \(\frac{q}{C_{1}}+\frac{q}{C_{2}}+\frac{q}{C_{3}}\) … (i)

If Cs is the capacitance of series combination, then V = \(\frac{q}{\mathrm{C}_{\mathrm{s}}}\).

So the equation (i) becomes
\(\frac{q}{\mathrm{C}_{\mathrm{s}}}=\frac{q}{\mathrm{C}_{1}}+\frac{q}{\mathrm{C}_{2}}+\frac{q}{\mathrm{C}_{3}}\)
Or
\(\frac{1}{\mathrm{C}_{\mathrm{s}}}=\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}+\frac{1}{\mathrm{C}_{3}}\)

(b) In the circuit shown in the figure, the charge on the capacitor of 4 μF is 16 μC. Calculate the energy stored in the capacitor of 12 μF capacitance. (CBSE 2019C)

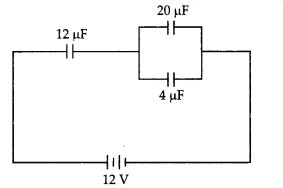
Answer:
Charge q across 4 μF Capacitor is 10 μc Potential difference across the capacitor of capacitance 4 μF will be
V= \(\frac{q}{C}=\frac{16 \mu C}{4 \mu F}=\frac{16 \times 10^{-6} \mathrm{C}}{4 \times 10^{-6} \mathrm{~F}}\)=4V

∴ Potential across 12 μF Capacitors
= 12V – 4V = 8V

Energy stored in the capacitors of capacitance C = 12 μF

U = \(\frac{1}{2}\) CV² = \(\frac{1}{2}\) × 12 × 10^-6 × 8² joule
= 384 × 10^-6 J = 384 μJ

Question 3.
Two identical plane metallic surfaces A and B are kept parallel to each other in the air, separated by a distance of 1 cm as shown in the figure.

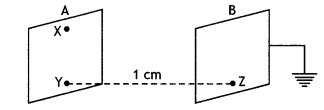
A is given a positive potential of 10 V and the outer surface of B is earthed.
(i) What is the magnitude and direction of the uniform electric field between Y and Z?
Answer:
The electric field between the plates is
E = \(\frac{V}{d}\) = 10³ V m^-1
directed from plate A at the higher potential to plate B at a lower potential, i.e. from Y to Z

(ii) What is the work done in moving a charge of 20 µC from X to Y?
Answer:
Since X and Y are on the same plate A, which is an equipotential surface, work done in moving a charge of 20 µC from X to Y on the equipotential surface is zero.

Question 4.
(i) Draw the equipotential surfaces corresponding to a uniform electric field in the z-direction.
Answer:
The equipotential surfaces are as shown.

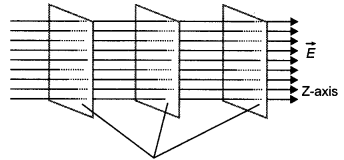
Equipotential surfaces

(ii) Derive an expression for the electric potential at any point along the axial line of an electric dipole. (CBSE Delhi 2019)
Answer:
Consider an electric dipole of length 2a and having charges +q and -q. Let us find the potential on the axial line at point P at a distance OP = x from the center of the dipole.

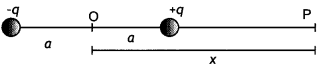
Now potential at point P is

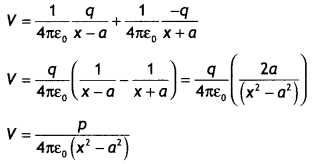
Question 5.
A network of four capacitors, each of capacitance 15 µF, is connected across a battery of 100 V, as shown in the figure. Find the net capacitance and the charge on the capacitor C₄. (CBSE Al 2012C)

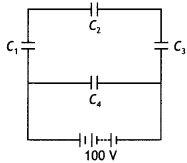
Answer:
Capacitors C1 C2 and C3 are in series, therefore their equivalent capacitance is
\(\frac{1}{C_{\mathrm{s}}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}=\frac{1}{15}+\frac{1}{15}+\frac{1}{15}=\frac{3}{15}\)

Hence C_S = 5 µF
Now C_S and C₄ are in parallel, hence
C_P = C_S + C₄ = 5 + 15 = 20 µF

Now C4 is connected to 100 V, therefore charge on it is
Q = CV=15 × 10^-6 × 100=15 × 10^-4 C

Question 6.
A parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor. (CBSE AI 2014)
Answer:
U_i = \(\frac{1}{2}\) CV²

When the capacitors are connected then the energy stored is
U_F = \(\frac{1}{2}\left(C_{1}+C_{2}\right)\left(\frac{C_{1} V_{1}+C_{2} V_{2}}{C_{1}+C_{2}}\right)^{2}\)

Since C₁ = C₂ = C, and V₂ = 0, we have
Uf = \(\frac{1}{2}(C+C)\left(\frac{C V}{C+C}\right)^{2}=\frac{1}{2}(2 C) \times \frac{V^{2}}{4}=\frac{1}{4} C V^{2}\)

Hence we have
\(\frac{U_{f}}{U_{i}}=\frac{1}{2}\)

Question 7.
An isolated air capacitor of capacitance C₀ is charged to a potential V₀. Now if a dielectric slab of dielectric constant K is inserted between its plates, completely filling the space between the plates, then how to do the following change, when the battery remains connected
(i) capacitance,
Answer:
When the battery remains connected, the potential on the capacitor does not change.
The capacitance of the capacitor becomes K times the original value, i.e. C = K C₀.

(ii) charge
Answer:
Now new charge is Q = CV = K C₀ V = K Q₀.

(iii) the field between the plates
Answer:
The field between the plates becomes
E = \(\frac{V}{d}=\frac{V_{0}}{d}\) = E₀, i.e. no change.

(iv) energy stored by the capacitor?
Answer:
The energy stored becomes
U = \(\frac{1}{2} C V^{2}=\frac{1}{2} K C_{0} V^{2}\) = KU₀.

Question 8.
An isolated air capacitor of capacitance C0 is charged to a potential V0. Now if a dielectric slab of dielectric constant K is inserted between its plates, completely filling the space between the plates, then how to do the following change, when the battery is disconnected
(i) charge
Answer:
If battery is disconnected then charge remains same, Q = Q₀

(ii) electric field between the plates,
Answer:
V = \(\frac{V_{0}}{K}\) ,
∴E = \(\frac{E_{0}}{K}\) ,

(iii) capacitance
C = KCO [∵ C = \(\frac{Q_{0}}{V}=\frac{Q_{0}}{V_{0} / K}=\frac{K Q_{0}}{V_{0}}\)]

(iv) energy stored by the capacitor
U = \(\frac{U_{0}}{K}\left[U=\frac{1}{2} C V^{2}=\frac{1}{2}\left(K C_{0}\right)\left(\frac{V_{0}}{K}\right)^{2}\right]\)

Question 9.
The figure shows two identical capacitors, C₁ and C₂, each of 1 µF capacitance connected to a battery of 6 V. Initially switch ‘S’ is closed. After some time ‘S’ is left open and dielectric slabs of dielectric constant K = 3 are inserted to fill completely the space between the plates of the two capacitors. How will (i) the charge and (II) potential difference between the plates of the capacitors be affected after the slabs are inserted? (CBSE Delhi 2011)

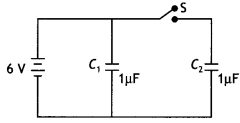
Answer:
When switch S is opened then capacitor C₁ remains connected to the battery white capacitor C₂ is disconnected. Thus for the two capacitors, we have

Physical quantity	Capacitor C1	Capacitor C2
Charge	Becomes K times, i.e. Q = CV = K C0V = 3 × 1 × 10-6 × 6 = 1.8 × 10-5 C	Remains same Q = Q0  = CV = 1 × 10-6 × 6 = 6 × 10-6 C
Potential difference	Remains same V = V0 = 6 V	Becomes 1/K times V =V0/K = 6/3 = 2V

Question 10.
A particle, having a charge +5 µC, is initially at rest at the point x = 30 cm on the x axis. The particle begins to move due to the presence of a charge Q that is kept fixed at the origin. Find the kinetic energy of the particle at the instant it has moved 15 cm from its initial position if (i) Q = +15 µC and (ii) Q = -15 µC (CBSE Sample Paper 2018-19)
Answer:
From energy conservation, U_i + K_i = U_f + K_f
kQq/r_i + 0 = kQq/r_f + K_f
K_f = kQq (1/r_i — 1/r_f)

When Q is +15 µC, q will move 15 cm away from it. Hence r_f = 45 cm
K_f = 9 × 10⁹ × 15 × 10^-6 × 5 × 10^-6 [1/(30 × 10^-6) – 1/(45 × 10^-2)] = 0.75 J

When Q is -15 µC, q will move 15 cm towards it. Hence r_f = 15 cm K_f = 9 × 10⁹ × (-15 × 10^-6) × 5 × 10⁶ [1/(30 × 10^-2) – 1/(15 × 10^-2)] = 2.25 J

Question 11.
Two metal spheres, one of radius R and the other of radius 2R, both have same surface charge density σ. They are brought in contact and separated. What will be new surface charge densities on them? (NCERT Exemplar)
Answer:
Let the two spheres have charges Q₁ and Q₂ respectively. Since σ₁ = σ₂, before contact, we have
\(\frac{Q_{1}}{4 \pi R^{2}}=\frac{Q_{2}}{4 \pi(2 R)^{2}}\)
Or
Q₂ = 4 Q₁

After contact
Let q1 and q2 be the charges on them, then
q₁ + q₂ = Q₁ + Q₂= Q₁ + 4Q₁ = 5Q₁ = 5(σ × 4πr²)

The two will exchange charge till their potentials are equal, therefore we have
\(\frac{q_{1}}{R}=\frac{q_{2}}{2 R}\)
Or
q₂ = 2 q₁

Therefore 3q₁ = 5(σ × 4πr²)
Or
q₁ = \(\frac{5}{3}\)(σ x 4πr²) and q₂ = 2q₁ = \(\frac{10}{3}\)5(σ x 4πr²)

Therefore
σ₁ = \(\frac{q_{1}}{4 \pi R^{2}}=\frac{5}{3}\left(\frac{\sigma \times 4 \pi R^{2}}{4 \pi R^{2}}\right)=\frac{5 \sigma}{3}\)
And
σ₂ = \(\frac{q_{2}}{4 \pi(2 R)^{2}}=\frac{10}{3}\left(\frac{\sigma \times 4 \pi R^{2}}{4 \pi(2 R)^{2}}\right)=\frac{5 \sigma}{6}\)

Question 12.
(a) Derive an expression for the capacitance of a parallel plate capacitor when the space between the plates is partially filled with a dielectric medium of dielectric constant ‘K’.
Answer:
Consider a parallel plate capacitor having each plate of area A and separated by a distance d. When there is a vacuum between the two plates, the capacitance of the parallel plate capacitor is given by
C₀ = ε₀ A/d.

Suppose that when the capacitor is connected to a battery, the electric field of strength E₀ is produced between the two plates of the capacitor. Further, suppose that when a dielectric slab of thickness t (t < d) is introduced between the two plates of the capacitor as shown in the figure, the electric field reduces to E due to the polarisation of the dielectric. Therefore between the two plates of the capacitor, over a distance of t, the strength of the electric field is E, and over the remaining distance (d – f)

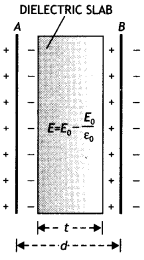
the strength is E₀. If V is the potential between the plates of the capacitor, then

V = E_t + E₀(d – t)
Since E = E₀/K where K is the dielectric constant, the above equation becomes

V = \(\frac{E_{0}}{K} t+E_{0}(d-t)=E_{0}\left(d-t+\frac{t}{K}\right)\)

The electric field between the plates of the capacitor is given by
E₀ = σ / ε₀ = Q/ A ε₀

Hence the potential between the two plates becomes.
V = \(E_{0}\left(d-t+\frac{t}{K}\right)=\frac{Q}{\varepsilon_{0} A}\left(d-t+\frac{t}{K}\right)\)

Hence the capacitance of the parallel plate capacitor is given

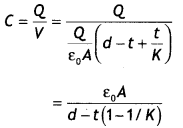
∴ clearly, C > C₀. Therefore, capacitance increases in the presence of a dielectric medium.

(b) Explain why the capacitance decreases when the dielectric medium is removed from between the plates.
Answer:
On removing the dielectric, the capacitance will decrease.

Question 13.
(a) Obtain the expression for the energy stored per unit volume in a charged parallel plate capacitor.
(b) The electric field inside a parallel plate capacitor is E. Find the amount of work done in moving a charge q over a closed rectangular loop a b c d a. (CBSE Delhi 2014)

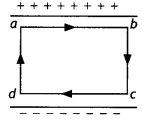
Answer:
(a) Suppose the capacitor is charged fully, its final charge is Q. and a final potential difference is V. These are related as Q = CV

Let q and V be the charge and potential difference, respectively.

At an intermediate stage during charging process q = CV. At this stage the small work done dW to transfer an additional charge dq is

dW = Vdq = \(\frac{q d q}{C}\)

The total work W needed to increase the capacitor’s charge q from zero to its final value Q is given by
W = \(\int_{0}^{w} d W=\int_{0}^{Q} \frac{q d q}{C}=\frac{1}{C} \int_{0}^{Q} q d q\)
Or
W = \(\frac{1}{C}\left|\frac{q^{2}}{2}\right|_{0}^{Q}=\frac{Q^{2}}{2 C}\)

This work is stored in the capacitor in the form of its electric potential energy. Hence,
U = \(\frac{Q^{2}}{2 C}\) … (1)

substituting Q = CV in equation (1) we have
U = \(\frac{1}{2}\) CV²

Energy density = Energy stored per unit volume

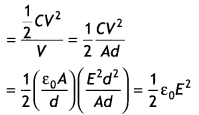
(b) Since the surface is an equipotential surface, work done is zero.

Question 14.
(a) Derive the expression for the capacitance of a parallel plate capacitor having plate area A and plate separation d.
Answer:
Suppose Q. is the charge on the capacitor, and c is the uniform surface charge density on each plate as shown in the figure. Therefore by Gauss’s theorem, the electric field between the plates of the capacitor (neglecting fringing of electric field at the edges) is given by

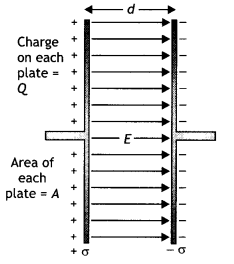
E = \(\frac{\sigma}{\varepsilon_{0}}=\frac{Q}{\varepsilon_{0} A}\) …. (1)

The field is uniform, and the distance between the plates is d, so the potential difference between the two plates is
V = Ed = \(\frac{1}{\varepsilon_{0}} \frac{Q d}{A}\) ….. (2)

Therefore by the definition of capacitance we have
C = \(\frac{Q}{V}=\frac{\varepsilon_{0} A}{d}\) …. (3)

This gives the capacitance of a parallel plate capacitor with a vacuum between plates.

(b) Two charged spherical conductors of radii R₁ and R₂ when connected by a conducting wire acquire charges q₁ and q₂ respectively. Find the ratio of their surface charge densities in terms of their radii. (CBSE Delhi 2014)
Answer:

The ratio of the surface charge densities is given by
\(\frac{\sigma_{1}}{\sigma_{2}}=\frac{q_{1}}{4 \pi R_{1}^{2}} \times \frac{4 \pi R_{2}^{2}}{q_{2}}\) ….(4)

Now when they are connected with a wire, their potentiaLs wilt be same: therefore, from the expression.
V = \(\frac{Q}{c}=\frac{Q}{R}\)

∵ C = 4πε₀R for a spherical body
∴\(\frac{q_{1}}{q_{2}}=\frac{R_{1}}{R_{2}}\)

Substituting in equation (4) we have
\(\frac{\sigma_{1}}{\sigma_{2}}=\frac{R_{1}}{R_{1}^{2}} \times \frac{R_{2}^{2}}{R_{2}}=\frac{R_{2}}{R_{1}}\)

Question 15.
(a) Describe briefly the process of transferring the charge between the two plates of a parallel plate capacitor when connected to a battery. Derive an expression for the energy stored in a capacitor.
Answer:
The electrons are transferred to the positive terminal of the battery from the metallic plate connected to the positive terminal, leaving behind a positive charge on it. Similarly, the electrons move on to the second plate from the negative terminal, hence it gets negatively charged. This process continues till the potential difference between the two plates becomes equal to the potential of the battery.

Suppose the capacitor is charged fully; its final charge is Q and the final potential difference is V.
These are related as Q = CV

Let q and V be the charge and potential difference respectively, after some time during the charging of the capacitor, then q = CV. At this time, the small work done dW required to transfer an additional charge dq is given by

dW = Vdq = \(\frac{q d q}{C}\)

The total work W needed to increase the capacitor’s charge q from zero to its final value Q is given by

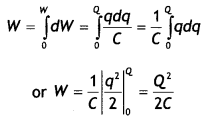
This work is stored in the capacitor in the form of its electric potential energy. Hence,
U = \(\frac{Q^{2}}{2 C}\) …(1)

Substituting Q= CVin equation (1) we have
U = \(\frac{1}{2}\) CV²

(b) A parallel plate capacitor is charged by a battery to a potential difference V. It is disconnected from the battery and then connected to another uncharged capacitor of the same capacitance. Calculate the ratio of the energy stored in the combination to the initial energy on the single capacitor. (CBSE Delhi 2019)
Answer:
The charge stored on the capacitor q = CV, when it is connected to the uncharged capacitor of same capacitance, sharing of charge, takes place between the two capacitors till the potential of both the capacitors becomes V/2.

Energy stored on the combination (U₂)
= \(\frac{1}{2} C\left(\frac{V}{2}\right)^{2}+\frac{1}{2} C\left(\frac{V}{2}\right)^{2}=C\left(\frac{V}{2}\right)^{2}=\frac{C V^{2}}{4}\)

Energy stored on single capacitor before connecting
U₁ = –\(\frac{1}{2}\) CV²

Ratio of energy stored in the combination to that in the single capacitor.
\(\frac{U_{2}}{U_{1}}=\frac{C V^{2} / 4}{C V^{2} / 2}=\frac{1}{2}\)

Question 16.
(a) Obtain the expression for the potential due to an electric dipole of dipole moment p at a point ‘x’ on the axial line.
(b) Two identical capacitors of plate dimensions l × b and plate separation d have dielectric slabs filled In between the space of the plates as shown In the figures.

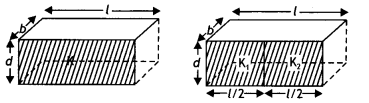
Obtain the relation between the dielectric constants K, K_1, and K₂. (CBSE Al 2013C)
Answer:
(a) Consider an electric dipole of length 2a and having charges + q and — q. Let us find the potential on the axial Une at point P at a distance OP = x from the center of the dipole.

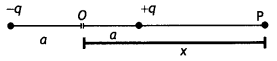
Now potential at point P is

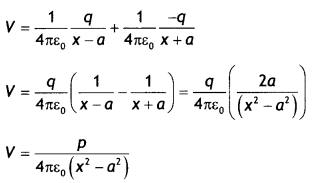
(b) When there is no dieLectnc then
C = \(\frac{\varepsilon_{0} l b}{d}\)

For the first capacitor
C’ = \(\frac{K \varepsilon_{0} l b}{d}\) = KC

The second case is a case of two capacitors connected in paralleL, therefore
C₁ = \(\frac{K_{1} \varepsilon_{0} l b}{2 d}\) and
C₂ = \(\frac{K_{2} \varepsilon_{0} l b}{2 d}\)

These two are connected in parallel, therefore we have
C” = C₁ + C₂ = \(\frac{K_{1} \varepsilon_{0} l b}{2 d}\) + \(\frac{K_{2} \varepsilon_{0} l b}{2 d}\)
= C\(\left(\frac{K_{1}+K_{2}}{2}\right)\)

If the capacitance in each case be same, then C’ = C”

Hence K= \(\left(\frac{K_{1}+K_{2}}{2}\right)\)

Question 17.
(a) Explain using suitable diagrams the difference in the behavior of a
(i) conductor:
Answer:
The diagram is as shown.

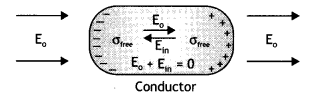
When a conductor is placed in an external electric field, the free charge carriers move and charge distribution in the conductor adjusts itself in such a way that the electric field due to induced charges opposes the external field within the conductor. This happens until in the static situation, the two fields cancel each other and the net electrostatic field in the conductor is zero.

(ii) dielectric In the presence of the external electric field. Define the term polarisation of a dielectric and write its relation with susceptibility.
Answer:

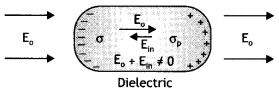
In a dielectric, this free movement of charges is not possible. It turns out that the external field induces dipole moment by stretching or re-orienting molecules of the dielectric. The collective effect of all the molecular dipole moments is that the net charges on the surface of the dielectric produce a field that opposes the external field. However, the opposing field so induced does not exactly cancel the external field. It only reduces it. The extent of the effect depends on the nature of the dielectric.

Dielectric polarization is defined as the dipole moment per unit volume of a dielectric. It is related to susceptibility as P = χ_eε₀\(\vec{E}\)

(b) A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge is placed at its center C and another charge +2Q. outside the shell, at a distance r from the center as shown in the figure. Find (i) the force on the charge at the center of the shell and at the point A and

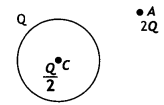
Answer:
(i) F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Q^{2}}{2 R^{2}}\) and
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{(Q+Q / 2) \times 2 Q}{r^{2}}\)

(ii) the electric flux through the shell. (CBSE Delhi 2015)
Answer:
Flux = \(\frac{Q}{2 \varepsilon_{0}}\)

Question 18.
(a) Define the SI unit of capacitance.
Answer:
The capacity of a capacitor is said to be one farad when a charge of 1 coulomb is required to raise the potential difference by 1 volt.

(b) Obtain the expression for the capacitance of a parallel plate capacitor.
Answer:
Let Q. be the charge on the capacitor, and o be the uniform surface charge density on each plate as shown in the figure.

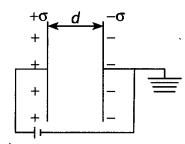
d = distance between plates of the capacitor.

Therefore by Gauss’ theorem, the electric field between the plates of the capacitor is given by
E = \(\frac{\sigma}{\varepsilon_{0}}=\frac{Q}{\varepsilon_{0} A}\)

The field is uniform, so the potential difference between the two plates is
V = Ed = \(\frac{1}{\varepsilon_{0}} \frac{Q d}{A}\)

Therefore, by the definition of capacitance we have
C = \(\frac{Q}{V}=\frac{\varepsilon_{0} A}{d}\)

This gives the capacitance of a parallel plate capacitor.

(c) Derive the expression of the effective capacitance of a series combination of n capacitance (CBSE Delhi 2016C)
Answer:
Capacitors in series. Capacitors are said to be connected in series if the second plate of one capacitor is connected to the first plate of the next and so on as shown in the figure.

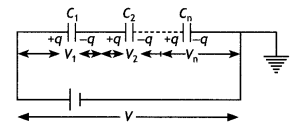
Resultant capacitance will be
\(\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\ldots \ldots \ldots \ldots=+\frac{1}{C_{n}}\)

Question 19.
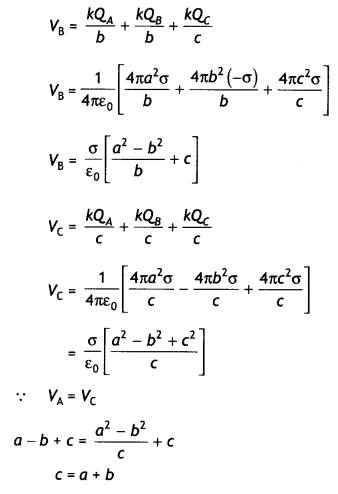
A charge Q is distributed over the surfaces of two concentric hollow spheres of radii r and R (R >> r), such that their surface charge densities are equal. Derive the expression for the potential at the common center.
Or
Three concentric metallic shells A, B, and C of radii a, b, and c (a <b < C) have surface charge densities +a, -a, and + o respectively as shown. Obtain the expressions for the potential of three shells A, B, and C. If shells A and C are at the same potential, obtain the relation between a, b and c. (CBSE Al 2019)

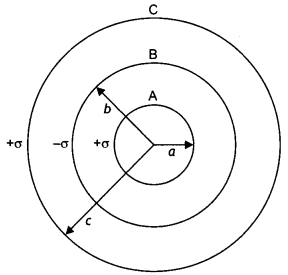
Answer:
Let the charges on the spheres be q, and q2 such that
Q=q₁ + q₂
= 4πσ(r² + R²)
Or
σ = \(\frac{Q}{4 \pi\left(r^{2}+R^{2}\right)}\)

Now potential at the common centre V=V₁ + V₂
V = \(\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{q_{1}}{r}+\frac{q_{2}}{R}\right)\)
= \(\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{4 \pi r^{2} \sigma}{r}+\frac{4 \pi R^{2} \sigma}{R}\right)\)

V = \(\frac{(r+R) \sigma}{\varepsilon_{0}}\)

Substituting for o, we have

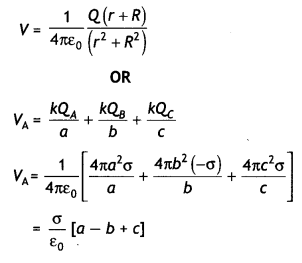
Numerical Problems :

Formulae for solving numerical problems

• V = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}\) electric potential at a point.
• Q = CV for a capacitor.
• C = 4πε₀R for a spherical conductor.
• C =\(\frac{Q}{V}=\frac{\varepsilon_{0} A}{d}\) capacitance of a parallel plate capacitor with air as dielectric.
• C = \(\frac{K \varepsilon_{0} A}{d}\) capacitance of a parallel plate capacitor with a dielectric.
• For capacitors in senes \(\frac{1}{C_{s}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\) and for capacitors in parallel C_p = C₁ + C₂
  
• U = \(\frac{1}{2} \frac{Q^{2}}{c}\) = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\)QV Energy stored in a capacitor.
• Energy density u = \(\frac{1}{2}\) ε₀E₂
  
• Capacitance of a parallel plate capacitor with a conducting slab of thickness t between plates is C = \(\frac{\varepsilon_{0} A}{d-t}\)
• Capacitance of a capacitor with dielectric slab of thickness t << d , C = \(\frac{\varepsilon_{0} A}{d+t\left(\frac{1}{K}-1\right)}\)
• Common potential V = \(\frac{C_{1} V_{1}+C_{2} V_{2}}{C_{1}+C_{2}}\)
• Loss of energy when two conductors are combined, U₁ – U₂ = \(\frac{C_{1} C_{2}}{2\left(C_{1}+C_{2}\right)}\left(V_{1}-V_{2}\right)^{2}\)
• If n small drops each having a charge Q, capacitance C, and potential V coalesce to form a big drop, then

1. The charge on the big drop = nQ
2. The capacitance of the big drop = n^1/3 C
3. Potential of the big drop = n^2/3 V
4. The potential energy of the big drop = n^5/3 U

Question 1.
Electric field intensity at point B due to a point charge Q kept at point A is 24 N C^-1 and the electric potential at point B due – to the same charge is 12 J C^-1. Calculate the distance AB and also the magnitude of the charge Q.
Answer:
Given E = 24 N C^-1 , V = 12 J C^-1 , r = ? and Q = ?

Using the relation
E = \(\frac { V }{ r }\)
Or
\(\frac { V }{ E }\) = \(\frac { 12 }{ 24 }\) = 0.5 m

Also V = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{r}\)

Therefore 12 = 9 × 10⁹ × \(\frac { Q }{ 0.5 }\) , solving for Q

we have Q = 6.67 × 10^-10C

Question 2.
A capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 360 μC. When the potential across the capacitor is reduced by 120 V, the charge stored in it becomes 120 μC. Calculate:
(i) The potential V and the unknown capacitance C.
(ii) What will be the charge stored in the capacitor, if the voltage applied had increased by 120 V? (CBSE Delhi 2013)
Answer:
Given Q₁ = 360 μC, Q₂ = 120 μC,
V₂ = (V- 120) volt, V₁ = V

(i) We know that C = \(\frac { Q }{ V }\)

Since capacitance is same, we have
\(\frac{Q_{1}}{V_{1}}=\frac{Q_{2}}{V_{2}}\)
Or
\(\frac{360 \times 10^{-6}}{V}=\frac{120 \times 10^{-6}}{V-120}\)

Solving for V we have V= 180 volt

Also C = Q₁/ V₁ = 360 × 10^-6 / 180 = 2 × 10^-6 C = 2 pF

(ii) V= 180 + 120 = 300 V
Therefore Q = CV = 2 x 10^-5 × 300 = 600 x 10^-6 = 600 pC

Question 3.
Two identical capacitors of 12 pF each are connected in series across a 50 V battery. Calculate the electrostatic energy stored in the combination. If these were connected in parallel across the same battery, find out the value of the energy stored in this combination. (CBSE Al 2019)
Answer:
Given C = 12 pF = 12 × 10^-12 F, V= 50 V,
In series
C_s = \(\frac{C_{1} C_{2}}{C_{1}+C_{2}}=\frac{12 \times 12}{12+12}\) = 6 pF

Hence energy stored
U_s = \(\frac{1}{2}\) C_sV₂ = \(\frac{1}{2}\) × 6 × 10^-12× (50)²
U_s = 7.5 × 10^-9 J

In parallel
C_P = C₁ + C₂ = 12 + 12 = 24 pF
U_P = \(\frac{1}{2}\) C_PV² = \(\frac{1}{2}\) × 24 × 10^-12 × (50)²
U_P = 3 × 10^-8 J

Question 4.
The figure shows a network of three capacitors C₁ = 2 μF; C₂ = 6 μF and C₃ = 3 μF connected across a battery of 10 V. If a charge of 6 μC is acquired by the capacitor C₃, calculate the charge acquired by C₁ (CBSE Al 2019)

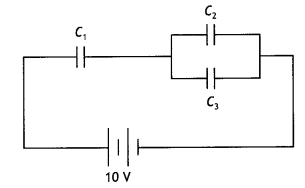
Answer:
Capacitors C₂ and C₃ are connected in parallel, therefore, the net capacitance of the combination.
C₂₃ = (6 + 3) = 9 μF

Let V1, be the potential across C1 and V2 be the potential across C₂₃
Now C₁ = Q/V, or V₁ = Q/C₁ = Q/2

Also V₂ = Q/9
But V = V₁ + V₂

Solving for Q we get
Q= 16.4 μC

Question 5.
(a) Find equivalent capacitance between A and B in the combination given below. Each capacitor is of 2 μF capacitance.

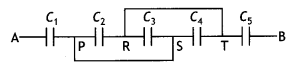
Answer:
This can be redrawn as

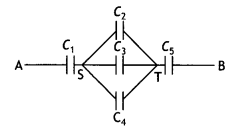
Like C₂, C₃ and C₄ are in parallel,
C₂₃₄ = C₂ + C₃ + C₄ = 6 μF

Further, C₁, C₂₃₄ and C₅ are in series
\(\frac{1}{C_{\text {net }}}=\frac{1}{2}+\frac{1}{6}+\frac{1}{2}=\frac{3+1+3}{6}=\frac{7}{6}\)
\(C_{\text {net }}=\frac{6}{7}\)μF

(b) If a DC source of 7 V is connected across AB, how much charge is drawn from the source and what is the energy stored in the network? (CBSE Delhi 2017)
Answer:
∴ C_net = \(\frac { 6 }{ 7 }\) μF ,

q = C_net V = \(\frac { 6 }{ 7 }\) × 10^-6 × 7 = 10^-6C

∴ Energy stored = \(\frac{1}{2}\)qV

= \(\frac{1}{2}\) × 6 × 10^-6 × 7 = 21 × 10^-6J

Question 6.
Two identical capacitors of 12 pF each are connected in series across a battery of 50 V. How much electrostatic energy is stored in the combination? If these were connected in parallel across the same battery, how much energy will be stored in the combination now? Also, find the charge drawn from the battery in each case. (CBSE Delhi 2017)
Answer:
(i) Net capacitance C_net = \(\frac{C_{1} C_{2}}{C_{1}+C_{2}}\)
= \(\frac{12 \times 12}{12+12}\)pF = 6 pF

∴ Energy stored = \(\frac{1}{2}\)C_net V²
= \(\frac{1}{2}\) × 6 × 10^-12 × (50)² = 75 × 10^-10J
q = Chargedrawn = C_net V=6 × 10^-12 × 50 = 3 × 10^-10 C

(ii) C_net=12 + 12 = 24pF
∴ Energy stored = \(\frac{1}{2}\) C_net V²
= \(\frac{1}{2}\) × 24 × 10^-12 × (50)²
= 3 × 10^-8J

Charge drawn, q = C_netV
= 24 × 10^-12 × 50
= 1200 × 10^-12
= 12 × 10^-10 C

Question 7.
In the following arrangement of capacitors, the energy stored in the 6 μF capacitor is E. Find the value of the following. (Foreign 2016)
(a) Energy stored in 12 pF capacitor.
(b) Energy stored in 3 pF capacitor.
(c) Total energy drawn from the battery.

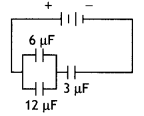
(a) Energy stored in 6 μ capacitor is E. Capacitors 6 μF and 12 μF are connected in parallel.
So, the voltage across 6 μF capacitor
= voltage across 12 μF capacitor
= voltage across 12 μF capacitor
= V (say)

As E = \(\frac{1}{2}\) × 6 × V²
∴ V = \(\sqrt{\frac{E}{3}}\)

Similarly energy U’ stored in 12 pF capacitor
= \(\frac{1}{2}\) × 12 × V²
= \(\frac{1}{2}\) ×12 × \(\frac{E}{3}\) = 2E

U’ = 2 E

(b) Equivalent capacitance of 6 µF and 12 µF is 6 + 12 = 18 µF

Charge on 18 µF and 3 µF is same as they are in series as they are in series
∴ Q = CV= 18 × V

∴ Energy in 3 µF capacitor
U” = \(\frac{1}{2} \frac{Q^{2}}{C}=\frac{1}{2} \frac{(18 V)^{2}}{3}\)

U” = \(\frac{1}{2} \times \frac{18 \times 18}{3} \frac{E}{3}\)
U” = 18E

(c) Total energy drawn from battery U = E + 2E + 18E = 21E

Question 8.
Two parallel plate capacitors X and Y have the same area of plates and the same separation between them, X has air between the plates, while Y contains a dielectric medium of ε_r = 4.
(a) Calculate the capacitance of each capacitor if the equivalent capacitance of the combination is 4 μF.

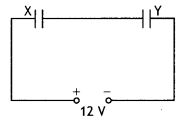
C_X = \(\frac{\varepsilon_{0} A}{d}\) = C(say)
C_Y= 4\(\frac{\varepsilon_{0} A}{d}\) = 4C

EquivaLent capacitance = 4 μF
C_eq = \(\frac{C_{X} C_{Y}}{C_{X}+C_{Y}}\) = 4
= \(\frac{C \times 4 C}{C+4 C}\)
Or
= \(\frac{4C}{5}\) = 4

C = 5 μF
∴ C_X = C = 5 μF and
C_Y = 4C = 20 μF

(b) Total charge, q = C_eq V = 4 × 12 = 48μC
C_X and C_Y are in series. Hence, charge on both is 48 μC each.

∴ The potential difference across C_X,
V_X = \(\frac{q}{C_{X}}=\frac{48}{5}\) = 9.6 V0lt

The potential difference across C_Y,
V_Y = \(\frac{q}{C_{Y}}=\frac{48}{20}\) = 2.4 Volt

(c) U_X=\(\frac{1}{2}\)CXVX² ; UY = \(\frac{1}{2}\)CYVy²

∴ \(\frac{U_{x}}{U_{Y}}=\frac{5 \times(9.6)^{2}}{20 \times(2.4)^{2}}\)
= \(\frac{1}{4} \times \frac{9.6 \times 9.6}{2.4 \times 2.4}\) = 4

\(\frac{U_{x}}{U_{r}}\) = 4

Question 9.
Find the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors C₁ and C₂ with their capacitances in the ratio 1:2 so that the energy stored in these two cases becomes the same. (CBSE Al 2016)
Answer:
(i) Let C₁ = C, ∴ C₂ = 2C
For series combination equivalent capacitance is
\(C_{s}=\frac{C_{1} \times C_{2}}{C_{1}+C_{2}}=\frac{C \times 2 C}{3 C}=\frac{2}{3} C\) …. (1)
and energy stored,
\(U_{\mathrm{s}}=\frac{1}{2} C_{s} V_{\mathrm{s}}^{2}=\frac{1}{2} \times \frac{2}{3} C V_{\mathrm{s}}^{2}\) …. (2)

For parallel combination equivalent capacitance
C_p = C + 2C = 3C ….(3)
and energy stored
∴ \(U_{D}=\frac{1}{2} 3 C \times V_{p}^{2}\) …(4)

But U_s = U_p [Given]

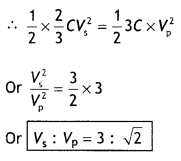
Question 10.
Calculate the potential difference and the energy stored in the capacitor C₂ in the circuit shown in the figure. Given potential at A is 90 V, C₁ = 20 μF, C₂ = 30 μF, and C₃= 15 μF. (CBSEAI 2015)

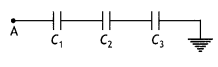
Answer:

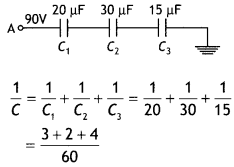
C = \(\frac{60}{9}\) μF = \(\frac{20}{3}\) μF

The potential at A = 90V

∴ Charge on each capacitor
Q = C x V= \(\frac{20}{3}\) x 90 =600 μC.

∴ Charge on C₂ = 600 μC

∴ V₂ = \(\frac{Q}{C_{2}}=\frac{600}{30}\) ; V₂ = 20 V

Energy stored in C₂ = \(\frac{1}{2}\)C₂V₂²

U₂ = \(\frac{1}{2}\) × 3o × 10^-6 × 20 × 20
U₂ = 6000 × 10^-6J = 6 × 10^-3J