Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 6 Electromagnetic Induction. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.
Class 12 Physics Chapter 6 Important Extra Questions Electromagnetic Induction
Electromagnetic Induction Important Extra Questions Very Short Answer Type
Question 1.
What is the function of a step-up transformer? (CBSE AI 2011C)
Answer:
The function of a step-up transformer is to step-up the alternating voltage.
Question 2.
State Lenz’s law. (CBSE AI 2012C)
Answer:
It states that the direction of induced emf is such that it opposes the cause of its production.
Question 3.
How can the self-inductance of a given coil having ‘N’ number of turns, area of cross-section of ‘A’ and length T be increased? (CBSE AI 2012C)
Answer:
By inserting a core of high permeability inside the coil.
Question 4.
How does the mutual inductance of a pair of coils change when
(a) the distance between the coils is increased and
(b) the number of turns in the coils is increased? (CBSE AI 2013)
Answer:
(a) decreases
(b) increases.
Question 5.
The motion of the copper plate is damped when it is allowed to oscillate between the two poles of a magnet. What is the cause of this damping? (CBSE AI 2013)
Answer:
Production of eddy current.
Question 6.
Why is the core of a transformer laminated? (CBSE Delhi 2013C)
Answer:
To reduce the effects of eddy currents.
Question 7.
A metallic piece gets hot when surrounded by a coil carrying a high-frequency alternating current. Why? (CBSE Delhi 2014C)
Answer:
Due to the production of eddy current which generates heat.
Question 8.
Name any two applications where eddy currents are used to advantage. (CBSE Delhi 2016C)
Answer:
- Electromagnetic damping
- Induction furnace.
Question 9.
A long straight current-carrying wire passes normally through the centre of the circular loop. If the current through the wire increases, will there be an induced emf in the loop? Justify. (CBSE Delhi 2017)
Answer:
Yes, as there will be a change in magnetic flux.
Question 10.
Predict the polarity of the capacitor in the situation described below. (CBSE AI 2017)
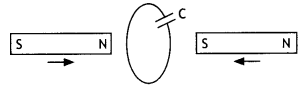
Answer:
The upper plate will be positive with respect to the lower plate in the capacitor.
Question 11.
In the figure given, mark the polarity of plates A and B of a capacitor when the magnets are quickly moved towards the coil. (CBSE AI 2017C)
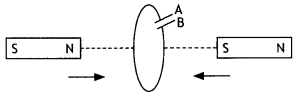
Answer:
Plate A will be positive with respect to plate B in the capacitor.
Question 12.
A long straight current-carrying wire passes normally through the centre of the circular loop. If the current through the wire increases, will there be an induced emf in the loop? Justify. (CBSE Delhi 2017)
Answer:
Yes, as there will be a change in magnetic flux.
Question 13.
An air-cored solenoid has self-inductance 2.8 H. When the core is removed, the self-inductance becomes 2 mH. What is the relative permeability of the core used? (CBSE Delhi 2017C)
Answer:
μr = 2.8 / 2 × 10-3 = 1.4 × 103
Question 14.
A choke and a bulb are in series to a dc source. The bulb shines brightly. How does its brightness change when an iron core is inserted inside the choke coil?
Answer:
There is no change in the brightness as the inductive reactance is zero for dc.
Question 15.
Why does the acceleration of a magnet falling through a long solenoid decrease?
Answer:
It decreases because of the opposing induced emf produced in the soLenoid due to the rate of change of magnetic flux.
Question 16.
Why is the core of a transformer laminated?
Answer:
It is done to reduce the effect of Eddy Currents.
Question 17.
A vertical metallic pole falls down through the plane of the magnetic meridian. Will any emf be Induced between Its ends?
Answer:
No emf will be induced because the pote neither intercepts the vertical component nor the horizontal component of the earth’s magnetic field.
Question 18.
A magnet Is moved towards a coil and an electric charge is induced in it. If the resistance of the coil is increased, how will the induced charge change?
Answer:
On increasing the resistance of the colt, the magnitude of induced charge decreases.
Question 19.
Can a transformer be used In a dc circuit?
Answer:
No, because there is no change in magnetic flux.
Question 20.
Why does a metallic piece become very hot when it is surrounded by a coil carrying high-frequency alternating current?
Answer:
The high-frequency coil induces eddy currents in the metallic piece. These eddy currents produce heat hence the metalLic piece becomes hot.
Question 21.
The figure shows a horizontal solenoid PQ connected to a battery and a switch. A copper ring R is placed on a frictionless track, the axis of the ring being along the axis of the solenoid. What would happen to the ring as the switch S is closed.
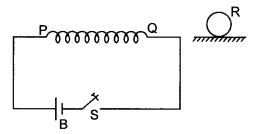
Answer:
The ring WilL be repelled due to opposing induced emf produced in it.
Question 22.
An air-core solenoid is connected to an ac source and a bulb. If an iron core Is inserted in the solenoid, how does the brightness of the bulb change? Give reasons for your answer.
Answer:
Insertion of an iron core In the solenoid increases its inductance. This in turn increases the value of inductive reactance. This decreases the current and hence the brightness of the bulb.
Question 23.
A magnet is moved in the direction indicated by an arrow between two coils AB and CD as shown in the figure. Suggest the direction of current in each coil,
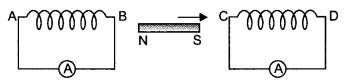
Answer:
In coil AB induced current flows from A to B and in colt CD current flows from C to D.
Question 24.
Predict the directions of induced currents in metal rings 1 and 2 lying in the same place where current I in the wire is increasing steadily. (CBSE Delhi 2012)
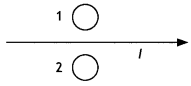
Answer:
1 -clockwise, 2-anticlockwise.
Question 25.
The electric current flowing in a wire In the direction from B to A is decreasing. Find out the direction of the induced current in the metallic loop kept above the wire as shown. (CBSE AI 2014)
Answer:
Clockwise.
Question 26.
Predict the polarity of plate A of the capacitor, when a magnet is moved towards it, as is shown In the figure. (CBSE AI 2014C)
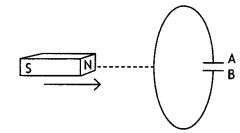
Answer:
Positive.
Question 27.
The figure below shows two positions of a loop PQR in a perpendicular uniform magnetic field. In which position of the coil is there induced emf?
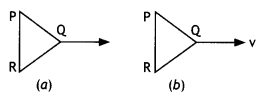
Answer:
In position b.
Question 28.
If the self-inductance of an air-core inductor increases from 0.01 mH to 10 mH on introducing an iron core into it, what is the relative permeability of the core used?
Answer:
We know that µ = \(\frac{L}{L_{0}}=\frac{10}{0.01}\) = 1000
Electromagnetic Induction Important Extra Questions Short Answer Type
Question 1.
An induced current has no direction of its own, comment.
Answer:
Yes, it is perfectly correct to say that an induced current has no fixed direction of its own. The direction of induced current depends upon the change in magnetic flux because in accordance with Lenz’s law the induced current always opposes the change in magnetic flux.
Question 2.
How are eddy currents produced? Mention two applications of eddy currents?
Answer:
Eddy currents are the currents induced in the body of a thick conductor when the magnetic flux linked with the conductor changes. When a thick conductor is moved in a magnetic field, magnetic flux linked with it changes. In situations like these, we can have induced currents that circulate throughout the volume of a material.
Because their flow patterns resemble swirling eddies in a river, therefore they are called eddy currents.
- Electromagnetic braking, and
- Induction furnace.
Question 3.
Name and define the unit used for measuring the coefficient of mutual inductance. State the relation of this unit with the units of magnetic flux and electric current.
Answer:
In SI the unit of mutual inductance is henry (H). Now from the expression
ε = – \(\frac{d \phi}{d t}\) = – M \(\frac{d l}{d t}\)
we have M = ε l \(\frac{d l}{d t}\).
Let ε = 1 volt and dl/dt = 1 As-1, then
M = 1 volt/1 As-1 = 1 henry.
The mutual-inductance of a coil is said to be 1 henry if a rate of change of current of 1 ampere per sec in the neighbouring coil induces in at an emf of 1 volt.
Question 4.
What are eddy currents? Write any two applications of eddy currents. (CBSE A! 2011)
Answer:
Eddy currents are the currents induced in the body of a thick conductor when the magnetic flux linked with a bulk piece of conductor changes.
- Dead Beat Galvanometer, and
- Induction furnace.
Question 5.
(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of the magnetic field B, area A and length l of the solenoid.
(b) How is this magnetic energy per unit volume compared with the electrostatic energy per unit volume stored in a parallel plate capacitor? (CBSE Delhi 2011C)
Answer:
The magnetic field stored in a solenoid is given by the expression U = – \(\frac{1}{2}\)Ll2.
But for a solenoid B = μ0nl
or
l = B / μ0 n
Substituting in the above expression we have
U = \(\frac{1}{2}\) × (μ0n2Al)\(\left(\frac{B}{\mu_{0} n}\right)^{2}\) as L = μ0 n2 A l
U = \(\frac{1}{2}\)\(\frac{B^{2} A l}{\mu_{0}}\)
We know that the energy stored per unit volume in a parallel plate capacitor is
UE = \(\frac{1}{2}\)ε0E2
It is clear that in both cases the energy stored per unit volume is proportional to the square of the field intensity.
Question 6.
State Lenz’s Law.
A metallic rod held horizontally along the east-west direction is allowed to fall under gravity. Will there be an emf induced at its ends? Justify your answer. (CBSE Delhi 2013)
Answer:
Lenz’s law states that the polarity of the induced emf is such that it tends to oppose the cause of its production.
Yes, as it will cut the horizontal component of the earth’s magnetic field.
Question 7.
Starting from the expression for the energy W = 1/2Ll2, stored in a solenoid of self-inductance L to build up the current l, obtain the expression for the magnetic energy in terms of the magnetic field B, area A and length l of the solenoid having n number of turns per unit length. Hence show that the energy density is given by 8z/2m0. (CBSE Delhi 2013C)
(i) The magnetic energy is
U = \(\frac{1}{2}\)LI2 = \(\frac{1}{2}\)L\(\left(\frac{B}{\mu_{0} n}\right)^{2}\) since B = μ0nl
Now L = μ0n2 Al, therefore we have
UB = \(\frac{1}{2}\)(μ0n2 Al)\(\left(\frac{B}{\mu_{0} n}\right)^{2}\) = \(\frac{1}{2 \mu_{0}} B^{2} A l\)
(ii) The magnetic energy per unit volume is
UB = \(\frac{U_{B}}{V}=\frac{U_{B}}{A l}=\frac{B^{2}}{2 \mu_{0}}\)
Question 8.
Define mutual inductance. A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, what is the change of flux linkage with the other coil? (CBSE Delhi 2016)
Answer:
Mutual inductance is numerically equal to the magnetic flux linked with a coil when the unit current passes through the neighbouring coil.
Given M = 1.5 H, dl = 20 – 0 = 20 A,
dt = 0.5 s, Φ = ?
Φ = – M\(\frac{d l}{d t}\)
or
Φ = – 1.5 × \(\frac{20}{0.5}\) = – 60 Wb
Question 9.
Explain the principle on which the metal detector is used at airports for security reasons.
Answer:
The metal detectors used in airport security checkpoints operate by detecting eddy currents induced in metallic objects. The detector generates an alternating magnetic field. This induces eddy currents in the conduction object carried through the detector. The eddy currents in turn produce an alternating magnetic field. This field induces a current in the detectors receiver coil.
Question 10.
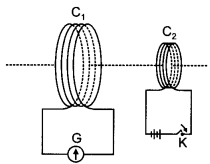
A current is induced in coil C1, due to the motion of current-carrying coil C2.
(i) Write any two ways by which a large deflection can be obtained in the galvanometer G.
(ii) Suggest an alternative device to demonstrate the induced current in place of a galvanometer. (CBSE Delhi 2011)
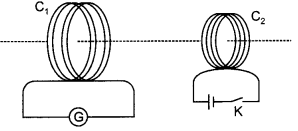
Answer:
(ii) The two ways are
(a) Passing a large current through coil C2 and
(b) Moving coil C2 quickly towards the coil.
(ii) A magnetic compass can be placed at the centre of coil C1. Whenever current will be induced it will show a deflection.
Question 11.
Consider a cube EFGHIJKL of side ‘a’ placed in a magnetic field B acting perpendicular to the face FJKG as shown in the figure. Write magnetic flux through the following faces (a) EFGH (b) EFJI (c) EILH (d) FJKG
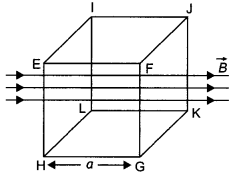
Answer:
The magnetic flux depends upon the angle (q) between the magnetic field and area vector.
(a) Here θ = 90°, therefore magnetic flux Φ = BA cos θ = BA cos 90° = 0
(b) Here θ = 90°, therefore magnetic flux Φ = BA cos θ = BA cos 90° = 0
(c) Here θ = 180°, therefore magnetic flux Φ = BA cos 180° = -BA
(d) Here θ = 0°, therefore magnetic flux Φ = BA cos 0° = BA
Question 12.
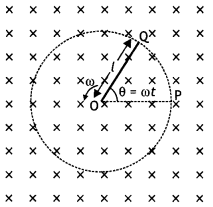
A metallic rod of ‘L’ length is rotated with an angular frequency of ‘ω’ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring. (CBSE Delhi 2012, 2013)
Answer:
Let the rod move from OP to OQ through a small sector of angle θ.
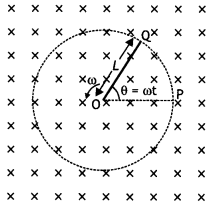
The small area covered by the rod is
dA= πL2 × \(\frac{\theta}{2 \pi}=\frac{1}{2}\)L2θ
where L is the radius of the circle in which the rod rotates. Hence the induced emf is
ε = \(\frac{d \phi}{d t}=\frac{d B A}{d t}=\frac{B d A}{d t}=B \frac{d}{d t}\left[\frac{1}{2} L^{2} \theta\right]\)
ε = – \(\frac{1}{2}\)L2B\(\frac{d \theta}{d t}=\frac{1}{2}\)BωL2
Question 13.
A metallic rod of length l length is rotated with a frequency ω, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius R = l, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf induced in the rod. If r is the resistance of the rod and the metallic ring has negligible resistance, obtain the expression for the power generated. (CBSE AI 2013C)
Answer:
For the first part refer above question.
The power generated is given by
P = \(\frac{\varepsilon^{2}}{r}=\frac{B^{2} \omega^{2} l^{4}}{2 r}\)
Question 14.
A rectangular loop PQMN with movable ‘ arm PQ of length 10 cm and resistance 4 Ω is placed in a uniform magnetic field of 0.25 T acting perpendicular to the plane of the loop as is shown in the figure. The resistances of the arms MN, NP and MQare negligible.
Calculate the
(i) emf induced in the arm PQand
(ii) current induced in the loop when arm PQ is moved with velocity 20 m s-1. (CBSE Delhi 2014C)
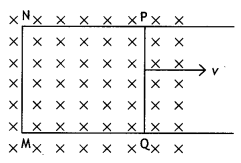
Answer:
Given L = 10 cm = 0.1 m, B = 0.25 T, v = 20 m s-1
(a) ε = BLv = 0.25 × 0.1 × 20 = 0.5 V
(b) l = ε/R = 0.5/4 = 0.125 A
Question 15.
In the given diagram a coil B is connected to a low voltage bulb L and placed parallel to another coil A as shown. Explain the following observations
(i) Bulb lights, and
(ii) Bulb gets dimmer if coil B is moved upwards.
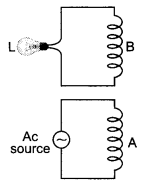
Answer:
(a) When ac is applied across coil A an induced emf is produced in coil B due to mutual induction between the two coils. This makes the lamp light up.
(b) When coil B is moved upwards the mutual induction and hence induced emf in coil B decreases. This makes the lamp dimmer.
Question 16.
A horizontal straight wire of length L extending from east to west is falling with speed v at right angles to the horizontal component of Earth’s magnetic field B.
(a) Write the expression for the instantaneous value of the emf induced in the wire.
Answer:
ε = BLv
(b) What is the direction of the emf?
Answer:
west to east
(c) Which end of the wire is at the higher potential? (CBSEAI2011)
Answer:
East.
Question 17.
Two concentric circular coils one of small radius r1 and the other of large radius r2, such that r1 << r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement. (NCERT)
Answer:
Let a current l2 flow through the outer circular coil. The field at the centre of the coil is B2 = \(\frac{\mu_{0} I_{2}}{2 r_{2}}\). Since the other coaxially placed coil has a very small radius, B2 may be considered constant over its cross¬sectional area. Hence,
Φ = πr1²B2 = \(\frac{\mu_{0} \pi r_{1}^{2} l_{2}}{2 r_{2}}\) = M12l2
Thus M12 = \(\frac{\mu_{0} \pi r_{1}^{2}}{2 r_{2}}\)
But M12 = M21, therefore M12 = M21 = \(\frac{\mu_{0} \pi r_{1}^{2}}{2 r_{2}}\)
Note that we calculated M12 from an approximate value of Φ1 assuming the magnetic field B2 to be uniform over the area πr1². However, we can accept this value because r1 << r2.
Question 18.
Consider a magnet surrounded by a wire with an on/off switch S (figure). If the switch is thrown from the off position (open circuit) to the on position (closed circuit), will a current flow in the circuit? Explain. (NCERT Exemplar)
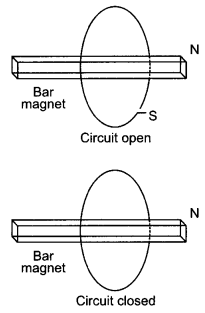
Answer:
There is no relative motion between the magnet and the coil. This means that there is no change in magnetic flux, hence no electromotive force is produced and hence no current will flow in the circuit.
Question 19.
A wire in the form of a tightly wound solenoid is connected to a DC source and carries a current. If the coil is stretched so that there are gaps between successive elements of the spiral coil, will the current increase or decrease? Explain. (NCERT Exemplar)
Answer:
The current will increase. As the wires are pulled apart the flux will leak through the gaps. Lenz’s law demands that induced e.m.f. resist this decrease, which can be done by an increase in current.
Question 20.
A solenoid is connected to a battery so that a steady current flows through it. If an iron core is inserted into the solenoid, will the current increase or decrease? Explain. (NCERT Exemplar)
Answer:
The current will decrease. As the iron core is inserted in the solenoid, the magnetic field increases and the flux increases. Lenz’s law implies that induced e.m.f. should resist this increase, which can be achieved by a decrease in current.
Electromagnetic Induction Important Extra Questions Long Answer Type
Question 1.
11 kW of electric power can be transmitted to a distant station at (i) 220 V or (ii) 22,000 V. Which of the two modes of transmission should be preferred and why? Support your answer with possible calculations.
Answer:
1. Consider that 11000 watt of energy has to be transmitted. First at 220 V and then at 22000 V. When the power is transmitted at 220 V then the current flowing through the wires is 11000/220 = 50 A
2. When power is transmitted at 22000 V then the current through the wires is 11000 / 22000 = 0.5 A. If R is the resistance of the line wire then the energy dissipated in the two cases is 2500R joule per sec and 0.25R. joule per sec.
This shows that if energy is transmitted at low voltages there is more loss in energy than when it is transmitted at high voltages. Furthermore, if power is to be transmitted at low voltage then the resistance of the line wire should be low, as such thick wires will be required. To support these thick wires strong poles situated close to each other will be needed. This will increase the cost of transmission. But at high voltages, even thin wires will do.
Question 2.
A coil A is connected to a voltmeter V and the other coil B to an alternating current source D. If a large copper sheet C is placed between the two coils, how does the induced emf in coil A change due to current in coil B. Justify your answer.
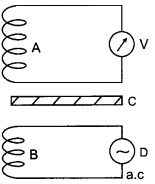
Answer:
In the absence of sheet C, an induced emf is set up in coil due to mutual induction phenomenon when an alternating current is passed through coil B.
However, when induced copper sheet C is placed, eddy currents are set up in the sheet due to a change in flux.
Thus, now coil A has a positive effect due to coil B and a negative effect due to eddy currents in C. Consequently, the flux of coil A and hence the induced emf in coil A is decreased, i.e. the reading of voltmeter V is reduced.
Question 3.
A bar magnet is dropped so that it falls vertically through coil C. The graph obtained for the voltage produced across the coil versus time is as shown in figure (b).
(i) Explain the shape of the graph and
(ii) why is the negative peak longer than the positive peak?
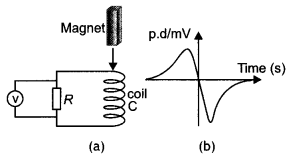
Answer:
(a) As the magnet approaches the coil, an emf is induced in it. As the magnet approaches the coil the magnetic flux linked with the coil increases. As a result the induced emf increases. When the magnet enters the coil, the change in magnetic flux linked with the coil begins to decrease and becomes zero when the magnet is completely inside the coil. This starts decreasing the emf and makes it zero.
When the magnet comes out of the coil the direction of induced emf changes direction and begins to increase in the opposite direction. When the magnet moves far away from the coil the induced emf becomes zero.
As the magnet comes out of the coil with a speed greater than the speed at which it approaches the coil, therefore the induced emf is more in the second case. Hence the longer negative peak.
Question 4.
(a) State Lenz’s law: Using this law indicate the direction of the current in a closed loop when a bar magnet with the North Pole is brought close to it. Explain briefly how the direction of the current predicted wrongly results in the violation of the law of conservation of energy.
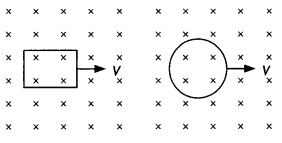
(b) A rectangular loop and circular loop are moving out of a uniform magnetic field region with a constant velocity v as shown in the figure. In which loop do you expect the induced emf to be constant during the passage out of the field region? The field is normal to the loops. (CBSE AI 2011C)
Answer:
(a) Lenz’s law states that the direction of the induced emf is such that it opposes the cause of its production. When the north pole of the magnet is brought near the coil, the upper end of the coil will acquire north polarity so as to oppose the approaching North Pole (by repelling). This means that the direction of current must be anticlockwise as seen from the side of the magnet.
If the current is wrongly predicted as clockwise, then the upper face will acquire south polarity which will attract the North Pole. This means the current is being produced without doing any work. This leads to the violation of the law of conservation of energy.
(b) It is expected that the induced emf will be constant in the rectangular coil. In the case of the rectangular coil, when pulled out of the magnetic field, the rate of change of magnetic flux will be constant because the rate of change of area is constant. This is not so in the case of the circular coil.
Question 5.
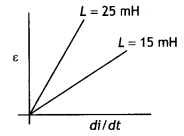
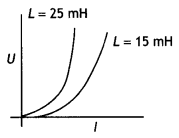
The current through two inductors of self-inductance 15 mH and 25 mH is increasing with time at the same rate. Draw graphs showing the variation of the
(a) emf induced with the rate of change of current
(b) energy stored in each inductor with the current flowing through it. Compare the energy stored in the coils, if the power dissipated in the coils is the same. (CBSE AI 2017C)
Answer:
Given L1 = 15 mH, L2 = 25 mH.
(a) The emf induced across an inductor is given by the expression ε = – L\(\frac{d i}{d t}\) since di/dt is the same for both coils therefore induced emf will depend upon the value of inductance. Hence the graphs are as shown
(b) The energy stored in an inductor is given by U = \(\frac{1}{2}\)Ll2
(c) The power dissipated P = l2XL
or
l2 = Pl XL and U = \(\frac{1}{2}\)Ll<sup>1</sup> = \(\frac{1}{2} \frac{L P}{X_{L}}=\frac{1}{2} \frac{P L}{\omega L}=\frac{P}{2 \omega}\)
Since power dissipated is same and co is also same therefore energy stored in the coils will also be the same.
Question 6.
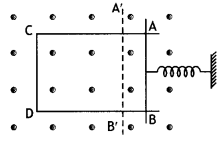
A rectangular frame of wire is placed in a uniform magnetic field directed outwards, normal to the paper. AB is connected to a spring which is stretched to AB and then released at time t = 0. Explain qualitatively how induced e.m.f. in the coil would vary with time. (Neglect damping of oscillations of spring) (CBSE AI 2018C)
Answer:
As the spring is released AB is pulled out of the field. This increases the area of the loop inside the magnetic field. This increases flux and hence an induced emf is produced. The portion AB does not stop at Ab but moves outwards. Now the spring will push AB inwards. This will decrease the area of the loop thereby decreasing the induced emf. This continues and hence the emf increases and decreases periodically.
Question 7.
Define mutual inductance between a pair of coils. Derive an expression for the mutual inductance of two long coaxial solenoids of the same length wound one over the other. (CBSE AI 2017)
Answer:
The mutual inductance of two coils is numerically equal to the magnetic flux linked with one coil when a unit current flows through the neighbouring coil.
As shown in the figure consider two long co-axial solenoids S1 and S2 with S2 wound over S1.
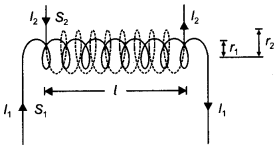
Let l = length of each solenoid r1, r2 = radii of the two solenoids
A = πr1² = area of cross-section of inner solenoid S1
N1, N2 = number of turns in the two solenoids First we pass a time-varying current l2 through S2. The magnet field set up inside S2 due to l2 is
B2 = μo n2 l2
where n2 = N2/l = the number of turns per unit length of S2.
Total magnetic flux linked with the inner solenoid S1 is
Φ1 = B2AN1 = μ0 n2 l2 × AN1
Mutual inductance of coil 1 with respect to coil 2 is
M12 = \(\frac{\phi_{1}}{l_{2}}\) = μ0n2AN1 = \(\frac{\mu_{0} A N_{1} N_{2}}{l}=\frac{\mu_{0} \pi r^{2} N_{1} N_{2}}{l}\)
The mutual inductance of any two coils is always proportional to the product N1 N2 of their number of turns. This is termed the reciprocity theorem.
Question 8.
Define mutual inductance and write its SI unit.
A square loop of side ‘a’ carrying a current l2 is kept at distance x from an infinitely long straight wire carrying a current l1 as shown in the figure. Obtain the expression for the resultant force acting on the loop. (CBSE Delhi 2019)
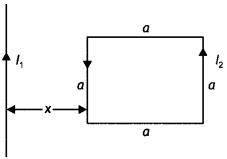
Answer:
(a) Mutual inductance equals the magnetic flux associated with a coil when unit current flows in its neighbouring coil. (b) Force per unit length between two parallel straight conductors
\(\frac{F}{L}=\frac{\mu_{o} I_{1} I_{2}}{2 \pi r}\)
Force on the part of the loop which is parallel to infinite straight wire and at a distance x from it F = \(\frac{\mu_{o} l_{1} l_{2} a}{2 \pi x}\)(away from the infinitely 2KX long wire)
Force on the part of the loop which is at a distance (x + a) from it
F2 = \(\frac{\mu_{0} I_{1} I_{2} a}{2 \pi(x+a)}\) (towards the infinite long wire)
Net force F = F1 – F2
F = \(\frac{\mu_{o} l_{1} l_{2} a^{2}}{2 \pi(x+a)}\) (away from the infinite straight line)
Question 9.
What are the possible causes of energy loss in a transformer? How are these minimised?
Answer:
The possible causes of energy losses in transformers are:
(a) Flux leakage: There is always some flux leakage. It can be reduced by winding the primary and secondary coils one over the other.
(b) Copper: The copper wires used for the windings have some resistance and hence some energy is lost due to heat produced in the wire. It can be minimised by taking thick wire.
(c) Eddy currents: The alternating magnetic flux induces eddy currents in the iron core, which results in loss of electrical energy. To minimise it we use a laminated iron core.
(d) Hysteresis loss: As the magnetisation cycle of the iron core is repeated again and again some loss of energy takes place due to magnetic hysteresis. To minimise it we prefer a soft iron core for which hysteresis loss is less.
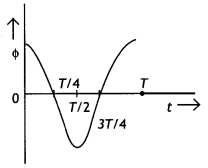
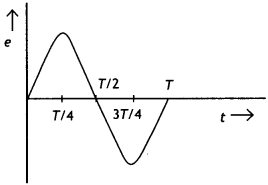
Question 10.
Discuss how Faraday’s law of e.m.f induction is applied in an ac generator for converting mechanical energy into electrical energy. Draw graphs to show the ’phase relationship’ between the instantaneous
(a) magnetic flux (Φ) linked with the coil and
(b) induced emf (ε) in the coil. (CBSE Delhi 2016C)
Answer:
In an ac generator, the change in magnetic flux is brought about by rotating the coil in a magnetic field. According to Faraday’s law, induced emf is set up in the coil on changing the magnetic flux linked with it. Hence mechanical energy, which is supplied to rotate the coil, gets converted into electrical energy.
Let the coil be rotated with a constant angular speed, co, the angle 0 between magnetic field 8, and area vector A of the coil at any instant is θ = ωt
Therefore magnetic flux at any instant is Φ = BA cos ωt
From Faraday’s law, induced emf is
ε = – n\(\frac{d \phi}{d t}\) = -nBA\(\frac{d}{d t}\)cos ωt
ε = nBAa sin ωt
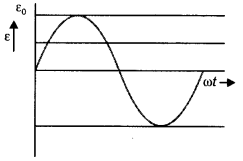
Magnetic flux is given by Φ = BA cos ωt, therefore the graph will be a cosine curve as shown
The induced emf is given by ε = nBA sin ωt, therefore the graph will be a sine curve as shown.
Question 11.
(a) Define self-inductance of a coil. Obtain an expression for the energy stored in a solenoid of self-inductance ‘L’ when the current through it grows from zero to l.
(b) A square loop MNOP of the side 20 cm is placed horizontally in a uniform magnetic field acting vertically downwards as shown in the figure. The loop is pulled with a constant velocity of 20 cm s-1 till it goes out of the field.
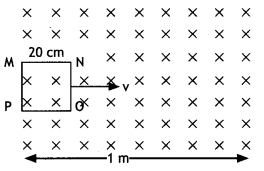
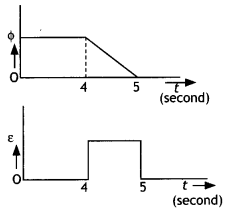
(c) Depict the direction of the induced current in the loop as it goes out of the field. For how long would the current in the loop persist?
(d) Plot a graph showing the variation of magnetic flux and induced emf as a function of time. (CBSE AI 2015)
Answer:
(a) Let i be the current at some instant through a pure inductor. If di / dt is the rate of change of current through the inductor then the voltage between the terminals of the inductor at this instant is
V=L di / dt
Therefore instantaneous power in the inductor is
P = Vab i = Li \(\frac{d i}{d t}\)
The energy dU supplied to the inductor during an infinitesimal time interval dt is
dU = P dt, so dU = Li di
The total amount of energy supplied while the current increases from zero to a final value l is
U = L ∫o1 i di = \(\frac{1}{2}\)L l2
(b) (i) Direction of induced current – clockwise (MNOP), the duration of induced current is 1s.
(ii) The graph is as shown.
Question 12.
(a) Define mutual inductance and write its SI units.
Answer:
The mutual inductance of two coils is numerically equal to the magnetic flux linked with one coil when a unit current flows through the neighbouring coil. It is measured in henry.
(b) Derive an expression for the mutual inductance of two long co-axial solenoids of the same length wound one over the other.
Answer:
The mutual inductance of two coils is numerically equal to the magnetic flux linked with one coil when a unit current flows through the neighbouring coil.
As shown in the figure consider two long co-axial solenoids S1 and S2 with S2 wound over S1.

Let l = length of each solenoid r1, r2 = radii of the two solenoids
A = πr1² = area of cross-section of inner solenoid S1
N1, N2 = number of turns in the two solenoids First we pass a time-varying current l2 through S2. The magnet field set up inside S2 due to l2 is
B2 = μo n2 l2
where n2 = N2/l = the number of turns per unit length of S2.
Total magnetic flux linked with the inner solenoid S1 is
Φ1 = B2AN1 = μo n2 l2 × AN1
Mutual inductance of coil 1 with respect to coil 2 is
M12 = \(\frac{\phi_{1}}{l_{2}}\) = μ0n2AN1 = \(\frac{\mu_{0} A N_{1} N_{2}}{l}=\frac{\mu_{0} \pi r^{2} N_{1} N_{2}}{l}\)
The mutual inductance of any two coils is always proportional to the product N1 N2 of their number of turns. This is termed the reciprocity theorem.
(c) In an experiment, two coils c1 and c2 are placed close to each other. Find out the expression for the emf induced in the coil c1 due to a change in the current through the coil c2. (CBSE Delhi 2015)
Answer:
Consider the experimental set up as shown.
When the key K is pressed in coil C1 a magnetic flux linked with C2 changes.
The magnetic flux linked with coil C2 is given by
f2 = M l1 where M is the mutual inductance between the two coils.
But by Faraday’s flux rule we have
ε2 = – \(\frac{d \phi}{d t}\) therefore we have
ε2 = – \(\frac{d M l_{1}}{d t}\) = – M \(\frac{d l_{1}}{d t}\)
Question 13.
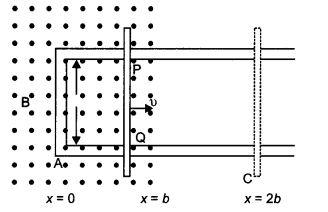
(a) When a bar magnet is pushed towards (or away) from the coil connected to a galvanometer, the pointer in the galvanometer deflects. Identify the phenomenon causing this deflection and write the factors on which the amount and direction of the deflection depend. State the laws describing this phenomenon.
(b) Sketch the change In flux, emf and force when a conducting rod PQ of resistance R and length I moves freely to and fro between A and C with speed v on a rectangular conductor placed in the uniform magnetic field as shown in the figure. (CBSE AI 2016)
Answer:
(a) Phenomenon: electromagnetic induction
Factors:
- Strength of the magnetic field of the magnet
- speed of motion of bar magnet.
Direction depends upon
- the motion of magnet whether inward or outward
- the direction of the north/south pole.
Law: The magnitude of the induced emf in a circuit is equal to the time rate of change of magnetic flux through the circuit.
(b) The sketch is as shown below.
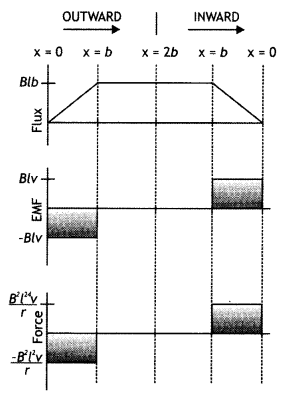
Question 14.
What is induced emf? Write Faraday’s laws of electromagnetic induction. Express it mathematically. A conducting rod of length ‘L’ with one end pivoted is rotated with a uniform angular velocity ‘ω’ in a vertical plane, normal to a uniform magnetic field ‘B’. Deduce an expression for the emf induced in this rod.
Answer:
It is the emf induced when the magnetic flux linked with a coil changes.
Faraday put forward the following laws called Faraday’s laws of electromagnetic induction.
- Law 1. Whenever the magnetic flux linked with a coil changes an induced emf is produced.
- Law 2. The induced emf lasts as long as the change in magnetic flux continues.
The expression for induced emf in rotating rod: Let the rod move from OP to OQ through a small sector of angle θ.
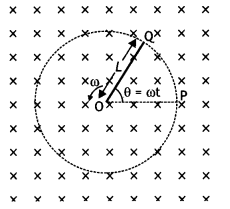
The small area covered by the rod is
dA = πL2 × \(\frac{\theta}{2 \pi}=\frac{1}{2}\)L2θ
where L is the radius of the circle in which the rod rotates. Hence the induced emf is
ε = \(\frac{d \phi}{d t}=\frac{d B A}{d t}=\frac{B d A}{d t}=B \frac{d}{d t}\left[\frac{1}{2} L^{2} \theta\right]\)
Or
ε = \(\frac{1}{2} L^{2} B \frac{d \theta}{d t}=\frac{1}{2}\)BωL2
Question 15.
How is the mutual inductance of a pair of coils affected when:
(a) the separation between the coils is increased?
Answer:
When the separation between the two coils is increased the mutual inductance decreases. It is because the flux linked with the secondary due to a current in the primary decreases.
(b) the number of turns of each coil is increased?
Answer:
When the number of turns of each coil is increased the mutual inductance increases because M12 (= M21) ∝ N1N2,
i.e. mutual inductance is directly proportional to the number of turns. The linkage of flux increases with an increase in the number of turns in the coils.
(c) a thin iron sheet is placed between the two coils, other factors remaining the same? Explain your answer in each case.
Answer:
When a thin iron sheet is placed between the coils the permeability of the medium between the coil increases. As mutual inductance is directly proportional to the permeability, therefore the mutual inductance increases.
Question 16.
A rectangular coil of area A, having a number of turns N, is rotated at f revolutions per second in a uniform magnetic field B, the field being perpendicular to the coil. Prove that the maximum emf induced in the coil is 2π f N B A.
Answer:
Consider an armature of the ac generator having n turns and placed in a uniform magnetic field B.
Suppose at any instant t the normal to the plane of the coil makes an angle 0 with the direction of the magnetic field. If ro is the uniform angular velocity with which, the coil rotates then θ = ωt.
The flux through the loop equals its area A multiplied by B⊥ = Bcos θ, the component of magnetic field B perpendicular to the area, hence
Φ = n B A cos Φ = n B A cos ω t …(1)
where is the number of turns in the armature?
By Faraday’s flux rule,
ε = – \(\frac{d \phi}{d t}=-\frac{d}{d t}\) n B A cos ω t
= – n B A \(\frac{d}{d \phi}\)cos ω t = – n B A (- ω sin ω t) ….(2)
Or
ε = n B A ω sin ω t
The induced emf is maximum when sin ωt = maximum = 1, therefore the maximum induced emf is given by
ε0 = n B A ω sin ω t …(3)
Since ω = 2πf, therefore equation (3) becomes ε0 = 2πf nBA
Question 17.
State Lenz’s law. Explain by giving examples that Lenz’s law is a consequence of the law of conservation of energy. (CBSE Delhi 2017C)
Answer:
It states that the direction of induced emf in a coil is such that it opposes the cause of its production. Lenz’s law is a consequence of the law of conservation of energy. To show it, let us consider a bar magnet pushed towards a conducting loop. When N-pole moves towards the loop, the face of the loop facing the North Pole develops north polarity as per Lenz’s law so as to oppose the motion of the magnet.
Again, when N-pole moves away from the loop, the nearby face develops south polarity, thus opposing the motion of the magnet away from the loop. It means that the motion of the magnet is automatically opposed every time. Hence, some work is to be done on the magnet to move it and this mechanical work is transformed into electrical energy. Thus, the conservation law of energy is followed.
Question 18.
Define the term ‘self-inductance’ and write its SI unit.
Obtain the expression for the mutual inductance of two long co-axial solenoids S1 and S2 wound one over the other, each of length L and radii r1 and r2 and n1 and n2 number of turns per unit length when a current I is set up in the outer solenoid S2. (CBSE Delhi 2017)
Answer:
The mutual inductance of two coils is numerically equal to the magnetic flux linked with one coil when a unit current flows through the neighbouring coil.
As shown in the figure consider two long co-axial solenoids S1 and S2 with S2 wound over S1.

Let l = length of each solenoid r1, r2 = radii of the two solenoids
A = πr1² = area of cross-section of inner solenoid S1
N1, N2 = number of turns in the two solenoids First we pass a time-varying current l2 through S2. The magnet field set up inside S2 due to l2 is
B2 = μo n2 l2
where n2 = N2/l = the number of turns per unit length of S2.
Total magnetic flux linked with the inner solenoid S1 is
Φ1 = B2AN1 = μo n2 l2 × AN1
Mutual inductance of coil 1 with respect to coil 2 is
M12 = \(\frac{\phi_{1}}{l_{2}}\) = μon2AN1 = \(\frac{\mu_{0} A N_{1} N_{2}}{l}=\frac{\mu_{0} \pi r^{2} N_{1} N_{2}}{l}\)
The mutual inductance of any two coils is always proportional to the product N1 N2 of their number of turns. This is termed the reciprocity theorem.
Question 19.
Obtain the expression for the magnetic energy stored in an ideal inductor of self-inductance L when a current l passes through it. Hence obtain the expression for the energy density of magnetic field B produced in the inductor. (CBSE Delhi 2016C)
Answer:
Let i be the current at some instant through a pure inductor. If di / dt is the rate of change of current through the inductor then the voltage between the terminals of the inductor at this instant is
V=L di / dt
Therefore instantaneous power in the inductor is
P = Vab i = Li\(\frac{d i}{d t}\)
The energy di supplied to the inductor during an infinitesimal time interval dt is
dU = P dt, so dU = Li di
The total amount of energy supplied while the current increases from zero to a final value l is
U = L ∫01 di = \(\frac{1}{2}\)L l2
This gives the expression for the energy stored in an inductor.
The magnetic energy is
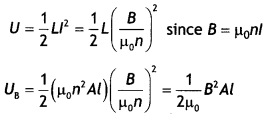
The magnetic energy per unit volume is
UB = \(\frac{U_{B}}{V}=\frac{U_{B}}{A l}=\frac{B^{2}}{2 \mu_{0}}\)
Question 20.
Derive the expression for the self-inductance of a solenoid.
Answer:
Consider a uniformly wound solenoid with N turns and length l. Let the length of the solenoid be large as compared to its radius and let the core of the solenoid have air. Due to this, we can take the interior field uniform. Therefore the magnetic field in the interior of the solenoid is given by
B = μ0 n l = μ0 \(\frac{N}{l}\) l …(1)
where n is the number of turns per unit length. The flux through each turn is given by
Φm = B A = μ0 \(\frac{N A}{l}\) l …(2)
where A Is the area of cross-section of the solenoid. But
L = \(\frac{N \Phi_{\mathrm{m}}}{I}\) …(3)
Therefore from equations (2) and (3) we have
L = \(\frac{N \Phi_{m}}{l}=\frac{\mu_{0} N^{2} A}{l}\) ….(4)
This shows that L depends on the geometric factors and is proportional to the square of the number of turns. Since N N = n l, we can therefore express the above result as
L = µ0\(\frac{(n l)^{2}}{l}\)A = µ0 n2 A l …(5)
Question 21.
(a) State Faraday’s laws of electromagnetic Induction.
Answer:
Faraday’s Laws of electromagnetic induction
First law: Whenever the magnetic flux (inked with a circuit (or coil) changes, an emf is induced in the circuit. The induced emf Lasts so Long as the change in the magnetic flux continues.
Second law:
The magnitude of induced emf in the circuit (or coil) is directly proportional to the rate of change of magnetic flux linked with the circuit.
i.e. e = – \(\frac{d \phi}{d t}\)
(b) Derive an expression for the emf induced across the ends of a straight conductor of length I moving at right angles to a uniform magnetic field B with a uniform speedy.
Answer:
Let a conductor ab of Length l be placed in a magnetic field \(\vec{B}\) shown by (x) directed towards the reader. When the conductor moves with velocity v perpendicular to B, the force on any free electron of this conductor is given
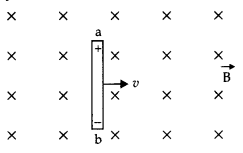
F = e vB sin 90° = evß
When this electron moves across the Length of the conductor, the work done by the electron
W = F × l = evBl
After some time when all the free electrons are shifted towards the end b, the end b becomes negative and end a becomes positively charged.
Hence the net induced emf in the conductor
e = \(\frac{W}{q}=\frac{e v B l}{e}=v B l\)
e = Blv
(c) Obtain the expression for the magnetic energy stored in a solenoid in terms of the magnetic field B, area A and length I of the solenoid through which a current j is passed. (CBSE 2019C)
Answer:
Energy stored in an inductor Considers an inductor of inductance L. Let I will be instantaneous current in the inductor and dl/dt be the rate of growth of current.
Induced emf, E = L\(\frac{dl}{dt}\) (in magnitude)
If the source sends a charge dq in time dt, then
dq = ldt
Small amount of work done by the source
dW = edq = eldt = L\(\frac{dl}{dt}\). ldt
or
dW = Ll dl
Total work was done during the growth of current in an Inductor by the external source
W = ∫dW =L∫01 ldl
= L \(\left[\frac{l^{2}}{2}\right]_{0}=\frac{1}{2}\)Ll2
W = \(\frac{1}{2}\) Ll2 …(1)
This work done is stored in the form of magnetic energy.
In a solenoid,
L = μ0n2Al
And B = μ0nl
∴ l = \(\frac{B}{\mu_{0} n}\)
So Eq. (1) becomes
W = \(\frac{1}{2}\)μ0n2Al\(\left(\frac{B}{\mu_{0} n}\right)^{2}=\frac{B^{2} A l}{2 \mu_{0}}\)
Question 22.
(a) A metallic rod of length ‘l’ and resistance ‘R’ is rotated with a frequency ‘v’ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius ‘l’, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field ‘B’ parallel to the axis is present everywhere.
(i) Derive the expression for the induced emf and the current in the rod.
(ii) Due to the presence of current in the rod and of the magnetic field, find the expression for the magnitude and direction of the force acting on this rod.
(iii) Hence, obtain an expression for the power required to rotate the rod.
(b) A copper coil l is taken out of a magnetic field with a fixed velocity. Will it be easy to remove it from the same field if its ohmic resistance is increased?
OR
(a) A rectangular coil rotates in a uniform magnetic field. Obtain an expression for induced emf and current at any instant. Also find their peak values. Show the variation of induced emf versus angle of rotation (ωt) on a graph.
(b) An iron bar falling through the hollow region of a thick cylindrical shell made of copper experiences a retarding force. What can you conclude about the nature of the iron bar? Explain. (CBSEAI 2019)
Answer:
(a) (/) Let the rod moves from OP to OQ through a small sector of angle θ.
The small area covered by the rod is
dA = πl2 × \(\frac{\theta}{2 \pi}=\frac{1}{2}\)l2θ
where L is the radius of the circle in which the rod rotates. Hence the induced emf is
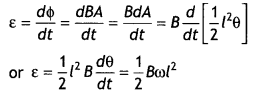
Now induced current is given by
i = \(\frac{\varepsilon}{R}=\frac{B \omega l^{2}}{2 R}\)
(ii) \(\vec{F}=i(\vec{l} \times \vec{B})\)
F = \(\frac{l^{3} \omega B}{2 R}\)
Direction of \(\vec{F}\) is perpendicular to both \(\vec{i}\) and \(\vec{B}\),
(iii) P = i2R
= \(\left(\frac{B l^{2} \omega}{2 R}\right)^{2}\)R = \(\frac{B^{2} l^{4} \omega^{2}}{4 R}\)
(b) Yes, since induced current will reduce, it will be a little easier to remove the coil.
Or
(a) Consider an armature of the ac generator having n turns placed in a uniform magnetic field B.
Suppose at any instant t the normal to the plane of the coil makes an angle θ with the direction of the magnetic field. If ω is the uniform angular velocity with which the coil rotates then θ = ωt.
The flux through the loop is Φ = n BA cos Φ = n BA cos ω t
where n is the number of turns in the armature.
By Faraday’s flux rule,
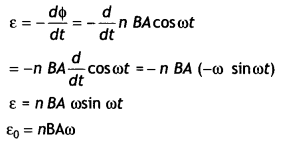
Now,i0 = \(\frac{\varepsilon_{0}}{R}=\frac{n B A \omega}{R}\)
The graph is as shown.
(b) The bar is magnetic in nature. It experiences retardation in accordance with Lenz’s law.
Question 23.
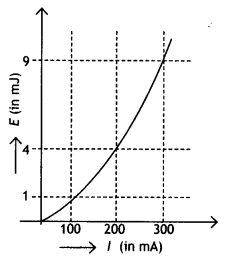
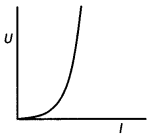
State Lenz’s law. The energy f required to build up a steady current l, in a given coil, varies with l in the manner as shown. Calculate the self-inductance of the coil.
A circular coil of radius r, is placed coaxially with another coil of radius R (R >> r) with the centre of the two coils coinciding with each other. Obtain an expression for the mutual inductance of the two coils.
Answer:
Lenz’s law states that the direction of induced emf is such that it opposes the cause of its production.
The energy stored in an inductor is given by the relation
E = – \(\frac{1}{2}\)Ll2
From the graph for a current of 200 mA the energy is 4 mJ, therefore self-inductance of the coil.
\(\frac{2 E}{l^{2}}\) = L
or
\(\frac{2 \times 4 \times 10^{-3}}{\left(200 \times 10^{-3}\right)^{2}}\) = 0.2 H
or
L = 200 mH
Consider the two coils of radius r and R placed coaxially, as shown in the figure.
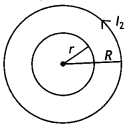
Let n1 and n2 be the number of turns per unit length in them.
If a current l2 is passed through the outer coil, there will a magnetic field
Bo = μo n1 l1 produced in it.
The flux associated with the inner coil will undergo variation as the field B0 grows.
The effective magnetic flux
Φ1 = Bo × Aeff = \(\frac{\mu_{0} l_{2}}{2 R}\) × πr²
Therefore mutual inductance of the coils is
M = \(\frac{\phi_{1}}{l_{2}}=\frac{\mu_{0} \pi r^{2}}{2 R}\)
Question 24.
(a) Describe a simple experiment (or activity) to show that the polarity of emf induced in a coil is always such that it tends to produce a current which opposes the change of magnetic flux that produces it.
(b) The current flowing through an inductor of self-inductance L is continuously increasing. Plot a graph showing the variation of
(i) Magnetic flux versus the current
(ii) induced emf versus dl/dt
(iii) Magnetic potential energy stored versus the current. (CBSE Delhi 2014)
Answer:
(a) Consider a coil C connected to a galvanometer. When the North Pole of a bar magnet is pushed towards the coil, the pointer in the galvanometer deflects, indicating the presence of electric current in the coil. When the magnet is pulled away from the coil, the galvanometer shows deflection in the opposite direction, which indicates a reversal of the current’s direction.
We see that the North Pole of a bar magnet is being pushed towards the closed coil. As the North Pole of the bar magnet moves towards the coil, the magnetic flux through the coil increases. Hence current is induced in the coil in such a direction that it opposes the increase in flux.
This is possible only if the current in the coil is in a counter-clockwise direction with respect to an observer situated on the side of the magnet. Similarly, if the North Pole of the magnet is being withdrawn from the coil, the magnetic flux through the coil will decrease. To counter this decrease in magnetic flux, the induced current in the coil flows in a clockwise direction and the South Pole faces the receding North Pole of the bar magnet. This would result in an attractive force that opposes the motion of the magnet and the corresponding decrease in flux.
(b) The graphs are as shown.
(i) Φ = Ll
Therefore the graph is
(ii) ε = – L\(\frac{dl}{dt}\)
Therefore the graph is
(iii) U = \(\frac{1}{2}\)Ll2
Therefore the graph is
Numerical Problems:
Formulae for solving numerical problems
- Induced emf ε = –\(\frac{d \phi}{d t}\)
or
ε = \(\frac{-\left(\phi_{2}-\phi_{1}\right)}{t_{2}-t_{1}}\) - Emf induced in a rod of Length L is ε = Blv.
- When a conducting rod of length L kept perpendicular to a uniform magnetic field B is rotated about one of its ends with uniform angular velocity, the emf induced between its ends has a magnitude
\(\frac{1}{2}\)BωL2 = BπvL2. - When a current in a coil changes, it induces a back emf in the same coil. The self-induced emf is given by
ε = – \(\frac{d \phi}{d t}\) = – L \(\frac{d l}{d t}\) inductance of the coil. It is a measure of the inertia of the coil against the change of current through it. Also Φ = L l - ε = – M\(\frac{d l}{d t}\) . Also Φ = Ml for mutual induction.
- \(\frac{V_{s}}{V_{p}}=\frac{N_{s}}{N_{p}}=\frac{l_{p}}{l_{s}}\) = k.
- Average power η = \(\frac{\varepsilon_{s} l_{s}}{\varepsilon_{p} l_{p}}\)
Question 1.
A square loop of side 10 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s-1 in the positive X-direction containing a magnetic field in the positive Z-direction. The field is non-uniform and has a gradient of 10-3 T cm-1 along the negative X-direction (i.e. it increases by 10-3 T cm-1 as one move in the negative X-direction). Calculate the emf induced. (CBSE 2019C)
Answer:

Question 2.
In a ceiling fan, each blade rotates in a circle of radius 0.5 m. If the fan makes 2 rotations per second and the vertical component of the earth’s magnetic field is 8 × 10-5 T, calculate the emf induced between the inner and outer ends of each blade. (CBSE2019C)
Answer:
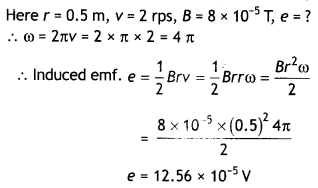
Question 3.
A circular coil of radius 10 cm, 500 turns and resistance 2 Ω are placed with its plane perpendicular to the horizontal component of the earth’s magnetic field. It is rotated about its vertical diameter through 180° in 0.25 s. Estimate the magnitudes of the emf and the current induced in the coil. The horizontal component of the earth’s magnetic field at the place is 3.0 × 10-5 T. (NCERT)
Answer:
Initial flux through the coil
Φin = BA cos θ = 3.0 × 10-5 × π × 10-2 × cos 0°
= 3π × 10-7 Wb
Final flux after the rotation
Φf = BA cos θ = 3.0 × 10-5 × π × 10-2 × cos 180° = – 3π × 10-7 Wb
Therefore estimated value of induced emf is
ε = n\(\frac{d \phi}{d t}\) = 500 × (6π × 10-7)/ 0.25 = 3.8 × 10-3 V dt
Hence the current induced is
l = ε/R = 3.8 × 10-3 / 2 = 1.9 × 10-3 A
Question 4.
Kamla peddles a stationary bicycle. The pedals of the bicycle are attached to a 100 turn coil of area 0.10 m2. The coil rotates at half a revolution per second and is placed in a uniform magnetic field of 0.01 T perpendicular to the axis of rotation of the coil. What is the maximum voltage generated in the coil? (NCERT)
Answer:
Given n = 100, A = 0.10 m2, B = 0.01 T, f = 0.5 rps
Using the expression ε0 = nBAω
we have ε0 = 100 × 0.01 × 0.10 × 2 × 3.14 × 0.5 = 0.314 V
Question 5.
A rectangular wire loop of sides 8 cm and 2 cm with a small cut is moving out of a region of the uniform magnetic field of magnitude 0.3 T directed normal to the loop. What is the emf developed across the cut if the velocity of the loop is 1 cm s-1 in a direction normal to the (a) longer side, (b) shorter side of the loop? For how long does the induced voltage last in each case? (NCERT)
Answer:
Given L = 8 cm = 8 × 10-2 m, b = 2 cm = 2 × 10-2 m, 8 = 0.3 T, v = 1 cm s-1 = 0.01 m s-1 ε = ?
(a) Using the expression ε = B L v
ε = 0.3 × 8 × 10-2 × 0.01 = 2.4 × 10-4 V
This emf will last till the loop comes out of the magnetic field. Since the shorter side is moving out, therefore it will take 2 s to cover 2 cm with a velocity of 1 cm s-1.
(b) Using the expression e = B L v
ε = 0.3 × 2 × 10-2 × 0.01 = 0.6 × 10-4 V
This emf will last till the loop comes out of the magnetic field. Since the longer side is moving out, therefore it will take 8 s to cover 8 cm with a velocity of 1 cm s-1.
Question 6.
A 1.0 m long metallic rod is rotated with an angular frequency 400 rad s-1 about an axis normal to the rod passing through its one end. The other end of the rod is in contact with a circular metallic ring. A constant and uniform magnetic field of 0.5 T parallel to the axis exists everywhere. Calculate the emf developed between the centre and the ring. (NCERT)
Answer:
Given L = 1.0 m, ω = 400 rad s-1, B = 0.5 T,
ε = ? Using the relation ε = \(\frac{1}{2}\)BωL2
we have
ε = \(\frac{1}{2}\)0.5 × 400 × 12 =100 V
Question 7.
A circular coil of radius 8.0 cm and 20 turns is rotated about its vertical diameter with an angular speed of 50 rad s-1 in a uniform horizontal magnetic field of magnitude 3.0 × 10-2 T. Obtain the maximum and average emf induced in the coil. If the coil forms a closed loop of resistance 10 Ω, calculate the maximum value of current in the coil. Calculate the average power loss due to Joule heating. Where does this power come from? (NCERT)
Answer:
Given r = 8.0 cm = 8.0 × 10-2 m, n = 20, ω = 50 rad s-1 B = 3.0 × 10-2 T, ε0 = ?, εa = ? R= 10 Ω l = ?, P = ?
Using the relation
ε0 = nBAω
= 20 × 3 × 10-2 × 3.14 × (8 × 10-2)2 × 50 = 0.603 V
The average induced emf is given by
εa = 0 over one cycle.
Also l0 = ε0 / R
= 0.603 / l0
= 0.0603 A
Now P = 1 /2 ε0 × l0 = 1 /2 × 0.603 × 0.0603
= 0.018 W
The induced current causes a torque opposing the rotation of the coil. An external agent (rotor) must supply torque to counter this torque in order to keep the coil rotating uniformly. Thus the source of the power dissipated as heat in the coil is the external rotor.
Question 8.
Current in a circuit falls from 5.0 A to 0. 0 A in 0.1 s. If an average emf of 200 V induced, give an estimate of the self-inductance of the circuit (NCERT)
Answer:
Given dl = 5.0 – 0.0 = 5.0 A, dt = 0.1 s, ε = 200 V, L = ?
Using the relation ε = – L \(\frac{dl}{dt}\)
or
L = \(\frac{\varepsilon}{d l / d t}\)
L = \(\frac{200}{5 / 0.1}=\frac{200 \times 0.1}{5}\) = 4 H
Question 9.
A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, what is the change of flux linkage with the other coil? (NCERT)
Answer:
Given dl = 20- 0.0 = 20 A, dt = 0.5 s, ε = ?,
M = 1.5 H,
Using the relation ε = – \(\frac{d \phi}{d t}\) = -M\(\frac{dl}{dt}\)
or
dΦ = Mdl = 1.5 × 20 = 30 Wb
Question 10.
A jet plane is travelling towards the west at a speed of 1800 km h-1. What is the voltage difference developed between the ends of the wing having a span of 25 m, if the earth’s magnetic field at the location has a magnitude of 5 × 10-4 T and the dip angle is 30°? (NCERT)
Answer:
Given v= 1800 km h-1, ε = ?, L = 25 m,
B = 5 × 10-4 T, δ = 30°
Now vertical component of earth’s magnetic field is
BV = B × sin 30°
= 5 × 10-4 × 0.5
= 2.5 × 10-4T
Now using the expression ε = B L v
ε = 2.5 × 10-4 × 25 × 500 = 3.125 V
Question 11.
1 MW power is to be delivered from a power station to a town 10 km away. One uses a pair of Cu wires of a radius of 0.5 cm for this purpose. Calculate the fraction of ohmic losses to the power transmitted if
(a) power is transmitted at 220 V. Comment on the feasibility of doing this.
(b) a step-up transformer is used to boost the voltage to 11000 V, power transmitted, then a step-down transformer is used to bring the voltage to 220 V. ρcu = 1.7 × 10-8 SI unit. (NCERT Exemplar)
Answer:
Given P = 1 MW, 2L = 20 km = 2 × 104 m, r = 0.5 cm = 0.5 × 10-2 m
(a) Resistance of the Cu wire used
R = \(\frac{\rho L}{A}=\frac{1.7 \times 10^{-8} \times 2 \times 10^{4}}{\pi \times\left(0.5 \times 10^{-2}\right)^{2}}\) = 4 Ω
Now current at 220 V is
l = \(\frac{P}{V}=\frac{10^{6}}{220}\) = 0.45 × 104 A
Therefore power loss
= l2R = (0.45 × 104)2 × 4 = 106W
This is a huge loss; therefore this method is not feasible.
(b) Now P = Vl’ or
l’ = \(\frac{P}{V^{\prime}}=\frac{10^{6}}{11000}=\frac{1}{1.1}\) × 102 A
Hence power loss
= l’2R = \(\frac{1}{1.21}\) × 4 × 104 = 3.3 × 104 W
Hence fraction of power loss
\(\frac{3.3 \times 10^{4}}{10^{6}}\) = 3.3%