Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 7 Alternating Current. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.
Class 12 Physics Chapter 7 Important Extra Questions Alternating Current
Alternating Current Important Extra Questions Very Short Answer Type
Question 1.
The instantaneous current flowing from an ac source is l = 5 sin 314 t. What is the rms value of current?
Answer:
The rms value of current is \(\frac{5}{\sqrt{2}}\).
Question 2.
The instantaneous emf of an ac source is given by E = 300 sin 314 t. What is the rms value of emf?
Answer:
The rms value of voltage is \(\frac{300}{\sqrt{2}}\)
Question 3.
Give the phase difference between the applied ac voltage and the current in an LCR circuit at resonance.
Answer:
The applied ac voltage and the current in an LCR circuit at resonance are in phase.
Hence phase difference = 0.
Question 4.
What is the phase difference between the voltage across the inductor and the capacitor in an LCR circuit?
Answer:
The phase difference is 180°.
Question 5.
What is the power factor of an LCR series circuit at resonance?
Answer:
The power factor is one.
Question 6.
In India, the domestic power supply is at 220 V, 50 Hz, while in the USA it is 110 V, 50 Hz. Give one advantage and one disadvantage of 220 V supply over 110 V supply.
Answer:
Advantage: less power loses
Disadvantage: more fatal.
Question 7.
Define the term ‘wattles current’. (CBSE Delhi 2011)
Answer:
It is the current at which no power is consumed.
Question 8.
In a series LCR circuit, VL = VC ≠ VR. What is the value of the power factor? (CBSE AI 2015)
Answer:
One.
Question 9.
Define capacitor reactance. Write its SI units. (CBSE Delhi 2015)
Answer:
It is the opposition offered to the flow of current by a capacitor. It is measured in ohm.
Question 10.
Define quality factor in series LCR circuit. What is its SI unit? (CBSE Delhi 2016)
Answer:
The quality factor is defined as the ratio of the voltage developed across the capacitor or inductor to the applied voltage. It does not have any unit.
Question 11.
A choke and a bulb are in series to a dc source. The bulb shines brightly. How does its brightness change when an iron core is inserted inside the choke coil?
Answer:
There is no change in the final brightness as the inductive reactance is zero for dc.
Question 12.
A solenoid with an iron core and a bulb are connected to a dc source. How does the brightness of the bulb change, when the iron core is removed from the solenoid?
Answer:
There Is no change In the finaL brightness as the inductive reactance is zero for dc.
Question 13.
In a serles LCR circult, the voltage across an inductor, capacitor and a resistor are 20 V, 20 V and 40 V, respectively. What Is the phase difference between the applied voltage and the current In the circuit?
Answer:
WhenVL = VC, then the circuit is in series resonance, therefore both current and voltage are in phase.
Question 14.
Why Is there no power consumption In an Ideal inductor connected to an ac source?
Answer:
This is because current and voltage across an ideal inductor are out of phase by 900.
Hence P = VRMS IRMS cos 90° = O
Question 15.
Can a choke be replaced by a capacitor of suitable capacitance?
Answer:
Yes, because even then the power consumed will be zero.
Question 16.
Find the inductance of the Inductor that would have a reactance of 50 ohm when used with an ac source of frequency 25/π kHz.
Answer:
Using XL = 2 πf L or L = \(\frac{X_{L}}{2 \pi f}\), therefore
L = \(\frac{50 \times \pi}{2 \pi \times 25}\) = 1 H
Question 17.
The figure gIven below shows the variation of an alternating emf with time. What Is the average value of the emf for the shaded part of the graph?
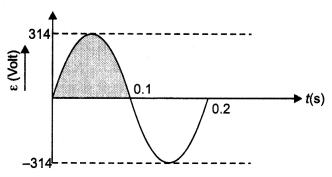
Answer:
Average or mean value of ac over half cycle or in time T/2 is
Em = 2Eo/π = 0.637 Eo = 0.637 × 314
or Em = 200 V.
Question 18.
What is the power dissipated in an ac circuit in which the voltage and current are given by V = 230 sin(ωt + π/2) and l = 10 sin ωt.
Answer:
Since the phase difference between the voltage and current is π/2, therefore power consumed = Vrms lrms cos π/2 = 0
Question 19.
When a lamp is connected to an alternating voltage supply, it lights with the same brightness as when compared to a 12 V dc battery. What Is the peak value of alternating voltage?
Answer:
The peak value is V = 12 × \(\sqrt{2}\) = 16.97 V
Question 20.
Why is the use of a.c. voltage preferred over d.c. voltage? Give two reasons. (CBSEAI 2014)
Answer:
- Can be increased or decreased easily.
- Can easiLy be converted into dc.
Question 21.
Can the Instantaneous power output of an ac source ever be negative? Can the average power output be negative?
Answer:
Yes, No.
Alternating Current Important Extra Questions Short Answer Type
Question 1.
State the phase relationship between the current flowing and the voltage applied in an ac circuit for (i) a pure resistor (ii) a pure inductor.
Answer:
- Electric current and voltage applied in a pure resistor are in same phase, i.e. Φ = 0°
- Applied voltage leads electric current flowing through pure-inductor in an ac circuit by phase angle of π/2.
Question 2.
A light bulb is in turn connected in a series (a) across an LR circuit, (b) across an RC circuit, with an ac source. Explain, giving the necessary mathematical formula, the effect on the brightness of the bulb in case (a) and (b), when the frequency of the ac source is increased. (CBSE 2019C)
Answer:
(a) The current in LR circuit is given by
l = \(\frac{V}{\sqrt{R^{2}+\omega^{2} L^{2}}}\)
When the frequency of ac source ω increases, l decreases, and hence brightness decreases.
(b) The current in RC circuit is given by
l = \(\frac{V}{\sqrt{R^{2}+\frac{1}{\omega^{2} C^{2}}}}\)
When the frequency of ac source ω increases, l increases, and hence brightness increases.
Question 3.
An air-core solenoid is connected to an ac source and a bulb. If an iron core is inserted in the solenoid, how does the brightness of the bulb change? Give reasons for your answer.
Answer:
Insertion of an iron core in the solenoid increases its inductance. This in turn increases the value of inductive reactance. This decreases the current and hence the brightness of the bulb.
Question 4.
A bulb and a capacitor are connected in series to an ac source of variable frequency. How will the brightness of the bulb change on increasing the frequency of the ac source? Give reason.
Answer:
When the frequency of the ac is increased, it will decrease the impedance of the circuit as Z = \(\sqrt{R^{2}+(1 / 2 \pi f C)^{2}}\). As a result, the current and hence the brightness of the bulb will increase.
Question 5.
An ideal inductor is in turn put across 220 V, 50 Hz, and 220 V, 100 Hz supplies. Will the current flowing through it in the two cases be the same or different?
Answer:
The current through the inductor is given by l = \(\frac{V}{X_{L}}=\frac{V}{2 \pi f L}\). The current is inversely proportional to the frequency of applied ac.
Since the frequency is different therefore the current will also be different.
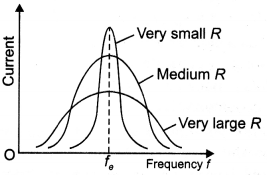
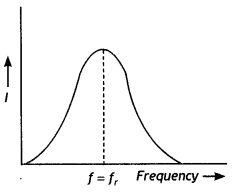
Question 6.
State the condition under which the phenomenon of resonance occurs in a series LCR circuit, Plot a graph showing the variation of current with a frequency of ac source in a series LCR circuit.
Answer:
The phenomenon occurs when the inductive reactance becomes equal to the capacitive reactance., i.e. XL – XC
⇒ ω L = \(\frac{1}{ωC}\)
⇒ ω = \(\frac{1}{\sqrt{L C}}\)
The graph is as shown below.
Question 7.
Give two advantages and two disadvantages of ac over dc.
Answer:
Advantages of ac:
(a) The generation and transmission of ac are more economical than dc.
(b) The alternating voltage may be easily stepped up or down as per need by using suitable transformers.
Disadvantages of ac:
(a) It is more fatal than dc.
(b) It cannot be used for electrolysis.
Question 8.
In a series, LCR circuit connected to an ac source of variable frequency and voltage v = vm sin ωt, draw a plot showing the variation of current (l) with angular frequency (ω) for two different values of resistance R1 and R2 (R1 > R2). Write the condition under which the phenomenon of resonance occurs. For which value of the resistance out of the two curves, a sharper resonance is produced? Define the Q-factor of the circuit and give its significance. (CBSE Delhi 2013C)
Answer:
The plot is as shown.
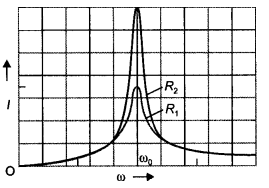
Resonance occurs in an LCR circuit when
XL = XC.
The smaller the value of R sharper is the resonance. Therefore the curve will be sharper for R2. It determines the sharpness of the resonance. The larger the value of Qsharper is the resonance.
Question 9.
You are given three circuit elements X, Y, and Z. When the element X is connected across an a.c. source of a given voltage, the current and the voltage are in the same phase. When the element Y is connected in series with X across the source, voltage is ahead of the current in phase by π/2. But the current is ahead of the voltage in phase by π/2 when Z is connected in series with X across the source. Identify the circuit elements X, Y, and Z. When all the three elements are connected in series across the same source, determine the impedance of the circuit. Draw a plot of the current versus the frequency of the applied source and mention the significance of this plot. (CBSE AI 2015)
Answer:
X-Resistor, Y-Inductor, Z-Capacitor For expression of the impedance of LCR circuit see X is a resistor
Y is a capacitor
Z is an inductor
Consider the impedance triangle
Z = \(\sqrt{R^{2}+\left(X_{t}-X_{C}\right)^{2}}\)
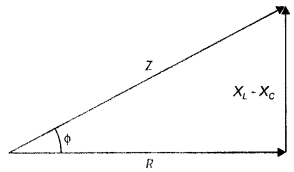
The plot is as shown.
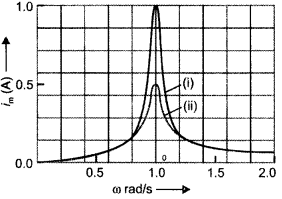
Significance, at ω = ω0 (resonance frequency) current, is maximum.
Question 10.
Given three elements X, Y, and Z to be connected across an ac source. With the only X connected across the ac source, voltage and current are found to be in the same phase. With only element Y in the circuit, the voltage lags behind the current in phase by π/2, while with the element Z in the circuit, the voltage leads the current in phase by π/2
(a) Identify the elements X, Y, and Z.
Answer:
X is resistor
Y is a capacitor
Z is an inductor
Consider the impedance triangle
Z = \(\sqrt{R^{2}+\left(X_{t}-X_{C}\right)^{2}}\)

(b) When all these elements are connected in series across the same source,
(i) determine the power factor,
Answer:
Power factor = cos Φ = R/Z
= \(\frac{R}{\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}}\)
(ii) find out the condition when the circuit is in resonant state. (CBSE AI 2019)
Answer:
Circuit will be in resonance when XL – XC = 0
Question 11.
A coil with an air core and an electric bulb are connected in series across a 220 V 50 Hz ac source. The bulb glows with some brightness. How will the glow of the bulb be affected by introducing a capacitor in series with the circuit? Justify your answer.
Answer:
The impedance of an LR circuit is given by the expression
Z = \(\sqrt{R^{2}+X_{L}^{2}}\) and
the impedance of a series LCR circuit is given by the expression
Z = \(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\).
Now current flowing through the two circuits is given by V
l = \(\frac{V}{Z}\).
Since Z decreases when a capacitor is connected to an LR circuit therefore there is an increase in current through the circuit. This increases the brightness of the bulb.
Question 12.
In the given circuit, inductor L and resistor R have identical resistance. Two similar electric lamps B1 and B2 are connected as shown. When switch S is closed,
(i) which one of the lamps lights earlier,
(ii) will the lamps be equally bright after some time? Justify your answer.
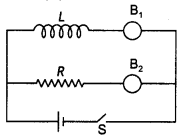
Answer:
(i) Lamp B2 connected with the resistor will light up first. This is because the current through the inductor will grow before attaining maximum value.
(ii) When the current through the inductor becomes maximum, after some time, both the lamps will be equally bright.
Question 13.
Figure (a), (b), and (c) show three ac circuits in which equal currents are flowing. If the frequency of emf be increased, how will the current be affected in these circuits? Give the reason for your answer.
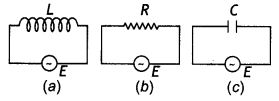
Answer:
There will be no change in the current in figure (b) as the resistance of the resistor does not depend upon the frequency of the applied ac.
The reactance of the inductor in figure (a) is given by XL = 2πf L. An increase in frequency increases the value of inductive reactance. This decreases the current through the circuit.
The reactance of the capacitor in figure (c) is given by XC = \(\frac{1}{\omega C}=\frac{1}{2 \pi f C}\). An increase in frequency decreases the value of capacitive reactance. This increases the current through the circuit.
Question 14.
An alternating voltage of frequency f is applied across a series LCR circuit. Let fr be the resonance frequency for the circuit. Will the current in the circuit lag, lead, or remain in phase with the applied voltage when (i) f > fr (ii) f < fr Explain your answer in each case.
Answer:
(i) When f > fr, then the circuit behaves as an inductive circuit. Thus emf leads current. This is because the inductive reactance is given by the expression XL = 2πfL. At high-frequency XL will be more.
(ii) When f < fr> then the circuit behaves as a capacitive circuit. Thus emf lags current. This is because the capacitive reactance is given by the expression XC = \(\frac{1}{2 \pi f C}\). This value is more at low 2πfC frequency.
Question 15.
For a series LCR circuit, connected to a sinusoidal ac voltage source, identify the graph that corresponds to ω > \(\frac{1}{\sqrt{L C}}\). Give reason.
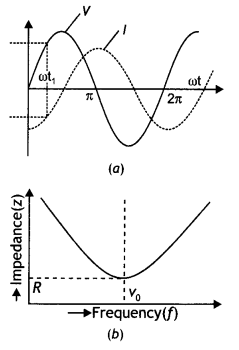
Answer:
When ω > \(\frac{1}{\sqrt{L C}}\), the circuit behaves as an inductive circuit. In an inductive circuit, emf leads current. This is depicted in the graph (a).
Question 16.
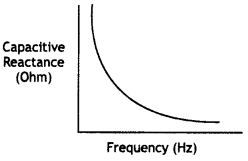
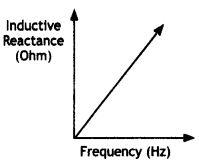
Draw the graphs showing the variations of (a) inductive reactance and (b) capacitive reactance, with the frequency of applied voltage in the ac circuit. How do the values of (a) inductive, and (b) capacitive reactance change, when the frequency of applied voltage is tripled?
Answer:
The graphs are as shown below.
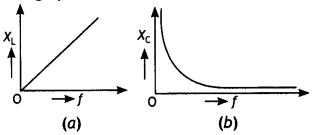
(a) The inductive reactance is given by the expression XL = 2πfL. Therefore if the frequency is tripled then the value of XL also gets tripled.
(b) The capacitive reactance is given by the expression XC = \(\frac{1}{2 \pi f C}\). Therefore if the frequency is tripled then the value of XC becomes one-third of its previous value.
Question 17.
Can the voltage drop across the inductor or the capacitor in a series LCR circuit be greater than the applied voltage of the ac source? Justify your answer.
Answer:
Yes, the voltage drop across the inductor or the capacitor in a series LCR circuit be greater than the applied voltage of the ac source. It is because the applied voltage is equal to the algebraic sum (as obtained by the use of a phasor diagram) of VR, VL, and VC, i.e.
V = l\(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\)
whereas VL = l XL and VC = l XC.
Thus, it is self-evident that VL or VC may be greater than V.
Question 18.
Mention the factors on which the resonant frequency of a series LCR circuit depends. Plot a graph showing the variation of the impedance of a series LCR circuit with the frequency of the applied ac source.
Answer:
In a series LCR circuit, the resonant frequency depends on the value of inductance L and capacitance C present in the circuit.
The graph showing the variation of impedance Z of a series LCR circuit with the frequency f of the applied ac source is shown below.
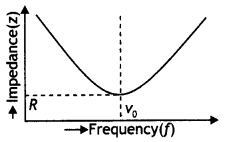
Question 19.
A lamp is connected in series with a capacitor. Predict your observations for dc and ac connections. What happens in each case if the capacitance of the capacitor is reduced? (NCERT)
Answer:
When a dc source is connected to a capacitor, the capacitor gets charged and after charging no current flows in the circuit and the lamp will not glow. There will be no change even if C is reduced. With ac source, the capacitor offers capacitive reactance (1/ωC), and the current flows in the circuit. Consequently, the lamp will shine. Reducing C will increase reactance and the lamp will shine less brightly than before.
Question 20.
A light bulb and an open coil inductor are connected to an ac source through a key as shown in the figure.
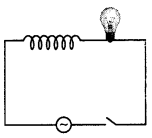
The switch is closed and after some time, an iron rod is inserted into the interior of the inductor. The glow of the light bulb (a) increases; (b) decreases (c) is unchanged as the iron rod is inserted. Give your answer with reasons. (NCERT)
Answer:
As the iron rod is inserted, the magnetic field inside the coil magnetizes the iron rod thereby increasing the magnetic field inside it. Hence, the inductance of the coil increases. Consequently, the inductive reactance of the coil increases. As a result, a larger fraction of the applied ac voltage appears across the inductor, leaving less voltage across the bulb. Therefore, the glow of the light bulb decreases.
Question 21.
Draw the effective equivalent circuit of the circuit shown in the figure at very high frequencies and find the effective impedance. (NCERT Exemplar)
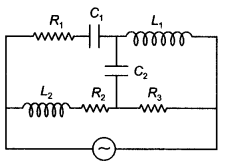
Answer:
At high frequency, the capacitive reactance is small while the inductive reactance is large. Therefore the capacitive reactance can be neglected while no current will flow through the inductors. Therefore the equivalent reactance of the circuit is Z = R1 + R3 and hence the circuit becomes
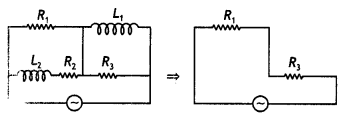
Question 22.
Study the circuits (a) and (b) shown in the figure and answer the following questions.
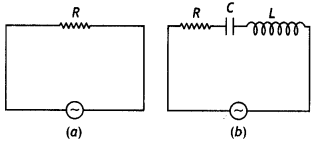
(a) Under which conditions would the rms currents in the two circuits be the same?
Answer:
This will happen when the impedance of both the circuits is the same, i.e. R. This is possible when circuit (b) is in resonance.
(b) Can the rms current in circuit (b) be larger than that in (a)? (NCERT Exemplar)
Answer:
No, because in circuit (b)
lrms = \(\frac{V_{\text {rms }}}{Z}=\frac{V_{\text {rms }}}{\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}}\), Z cannot be less than R.
Question 23.
How does the sign of the phase angle Φ, by which the supply voltage leads the current in an LCR series circuit, change as the supply frequency is gradually increased from very low to very high values? (NCERT Exemplar)
Answer:
The phase angle for an LCR circuit is given by the expression
tan Φ = \(\frac{R}{Z}=\frac{X_{L}-X_{C}}{R}=\frac{2 \pi f L-1 / 2 \pi f C}{R}\)
At low frequencies XL < XC and at high frequencies XL > XC Therefore Φ changes from negative to zero and to positive; zero at the resonant frequency.
Question 24.
A device ‘X’ is connected to an ac source. The variation of voltage, current, and power in one complete cycle is shown in the figure.
(a) Which curve shows power consumption over a full cycle?
(b) What is the average power consumption over a cycle?
(c) Identify the device ‘X’. (NCERT Exemplar)
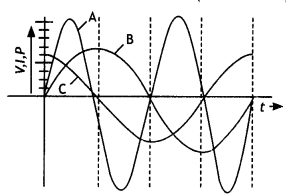
Answer:
(a) A
(b) Zero
(c) L or C or LC
Question 25.
Both alternating current and direct current are measured in amperes. But how is the ampere defined for an alternating current? (NCERT Exemplar)
Answer:
An ac current changes direction with the source frequency and the charge flow would average to zero. Thus, the ac ampere must be defined in terms of some property that is independent of the direction of the current. Joule’s heating effect is such property and hence it is used to define misvalue of ac.
Question 26.
A sinusoidal voltage of peak value 10 V is applied to a series LCR circuit In which resistance, capacitance, and inductance have values of 10 0, 1 μF, and 1 H, respectively.
Find (i) the peak voltage across the inductor at resonance
(ii) the quality factor of the circuit. (CBSE Sample Paper 2018-19)
Answer:
Given Vm = 10V, R = 1o Ω, L = 1 H, C = 1 μF,
VL = ?, Q = ?
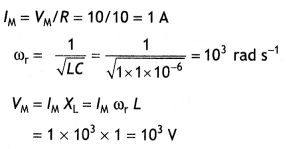
Q= ωr L/R = (103 × 1)/10 = 100
Question 27.
Draw a labeled diagram of a step-down transformer. State its working principle Write one main cause of energy loss in this device and the method used for reducing it.
Answer:
The labeled diagram is as shown.
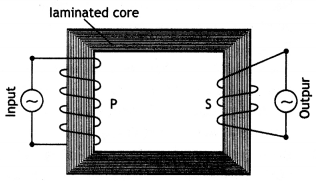
It works on the principle of mutual induction i.e., whenever magnetic flux linked with a coil changes an emf is induced in the neighboring coil.
One main cause of loss of energy is heat produced due to the production of eddy currents. This can be reduced by laminating the iron core.
Alternating Current Important Extra Questions Long Answer Type
Question 1.
Prove mathematically that the average power over a complete cycle of alternating current through an Ideal inductor is zero.
Answer:
Let the instantaneous value of voltage and current in the ac circuit containing a pure inductor are
V = Vm sin ωt and
l = lm sin (ωt – π/2) = – lm cos ωt
where π/2 is the phase angle by which voltage Leads currently when ac flows through an inductor. Suppose the voltage and current remain constant for a small-time dt. Therefore, the electrical energy consumed in the small-time dt is
dW = V l dt
The total electrical energy consumed in one time period of ac is given by

Therefore, the total electrical energy consumed in an ac circuit by a pure inductor is W = 0
Now average power is defined as the ratio of the total electrical energy consumed over the entire cycle to the time period of the cycle, therefore
Pav = \(\frac{W}{T}\) = 0
Hence, the average power consumed in an ac circuit by a pure inductor is Pav = 0
Thus a pure inductor does not consume any power when ac flows through it. Whatever energy is used in building up current is returned back during the decay of current.
Question 2.
Draw the phasor diagram of a series LCR connected across an ac source V= Vo sin ωt. Hence, derive the expression for the impedance of the circuit. Obtain the conditions for the phase angle under which the current is
(i) maximum and
(ii) minimum. (CBSE AI 2019)
Answer:
The voltages across the various elements are drawn as shown in the figure below.
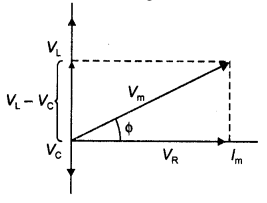
From the diagram, we observe that the vector sum of the voltage amplitudes VR, VL, and VC equals a phasor whose length is the maximum applied voltage Vm, where the phasor Vm makes an angle φ with the current phasor lm. Since the voltage phasors, VL and VC are in opposite direction, therefore, a difference phasor (VL – VC) is drawn which is perpendicular to the phasor VR. Adding vectorially we have
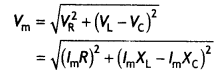
![]()
where XL = ω L and XC = 1 / ω C, therefore, we can express the maximum current as
lm = \(\frac{V_{\mathrm{m}}}{\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}}\)
The impedance Z of the circuit is defined as Z = \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{C}\right)^{2}}\)
For maximum lm, Z should be minimum (Z = R) or XC = XL = 0 and Φ = 0
For (lm)min Φ → 90° (|XC – XL| >> R) Z → ∞
Question 3.
(a) The graphs (i) and (ii) represent the variation of the opposition offered by the circuit element to the flow of alternating current with a frequency of the applied emf. identify the circuit element corresponding to each graph.
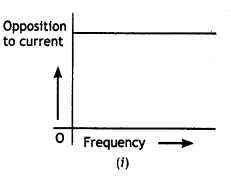
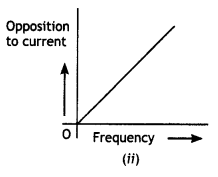
(b) Write the expression for the impedance offered by the series combinations of the above two elements connected across the ac source. Which will be ahead in phase in this circuit, voltage or current? (CBSE AI 2011C)
Answer:
(a) In figure (i) the opposition to the flow of current does not depend upon frequency, the circuit element is a resistor.
In figure (ii) the opposition increases with frequency, the current element is an inductor.
(b) When the resistor R and the inductance L are connected in series across an ac source, the impedance Z of the circuit is given by
Z = \(\sqrt{R^{2}+X_{L}^{2}}\), where XL is the inductive reactance.
In an L – R circuit, the voltage is ahead of the current.
Question 4.
An Inductor L of inductance XL is connected in series with bulb B and an ac source. How would the brightness of the bulb change when
(a) the number of turns In the Inductor Is reduced,
(b) an Iron rod Is Inserted Into the Inductor and
(c) a capacitor of reactance XC = XL
Is Inserted in series In the circuit. Justify your answer In each case. (CBSE Delhi 2015)
Answer:
(a) When the number of turns of the inductor reduced it decreases the inductance of the inductor as (L ∝ n2) where n is the number of turns. This in turn decreases the inductive reactance XL which increases the current in the circuit and hence the brightness of the bulb decreases.
(b) When an iron rod is inserted in the inductor, it increases the inductive reactance, which in turn decreases the current and hence the brightness of the bulb.
(c) When XL = XC, the circuit acts as a resistive circuit, i.e. the impedance becomes minimum and maximum current flows. This makes the bulb glow more brightly.
Question 5.
An inductor L of reactance XL is connected in series with a bulb B to an ac source as shown in the figure below. Briefly explain how the brightness of the bulb changes, when
(a) number of turns of the inductor Is reduced? and
(b) a capacitor of reactance XC = XL is included in series in the same circuit?
Answer:
If R is the resistance of the bulb, then the total impedance of the circuit is Z = \(\sqrt{R^{2}+X_{L}^{2}}\) and the corresponding current is l = V l Z.
(a) If the number of turns of the inductor is reduced then its inductance L and consequently there is a decrease in the reactance. This leads to a decrease in the impedance of the circuit. As a result the current flowing through the circuit increases. This increases the brightness of the bulb.
(b) When a capacitor of reactance XC = XL is included in the circuit, then the new impedance becomes Z = \(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\) = R. Thus the impedance has its minimum value. This increases the current through the circuit, which results in an increase in the brightness of the bulb.
Question 6.
A capacitor, ‘C’ a variable resistor ‘R’, and a bulb ‘B’ are connected in series to the ac mains in the circuit as shown. The bulb glows with some brightness. How will the glow of the bulb change if (a) a dielectric slab is introduced between the plates of the capacitor, keeping resistance R to be the same (b) the resistance R is increased keeping the same capacitance? (CBSE Delhi 2014)
Answer:
(a) As the dielectric slab is introduced between the plates of the capacitor, its capacitance will increase. Hence, the potential drop across the capacitor will decrease (V = Q/C). As a result, the potential drop across the bulb will increase (since both are connected in series). So, its brightness will increase.
(b) As the resistance (R) is increased, the potential drop across the resistor will increase. As a result, the potential drop across the bulb will decrease (since both are connected in series). So, its brightness will decrease.
Question 7.
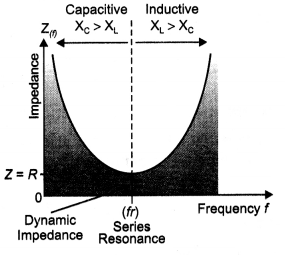
What is meant by impedance? Give its unit. Using a phasors diagram or otherwise derive the expression for the Impedance of an ac circuit containing L, C, and R in series. Find the expression for the resonant frequency.
Answer:
It is the opposition offered by LR or CR or LCR circuit to the flow of ac. It is measured in ohm.
For derivation of Z = \(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\)
The impedance Z of the circuit is defined as
Z = \(\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}\)
The graph is shown.
The current through an LCR circuit is given by the expression lv = \(\frac{E_{v}}{Z}\)
where Z is the impedance. Substituting the value of Z in the above equation we have
lv = \(\frac{E_{v}}{\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}}\)
Because the impedance depends on the frequency of the source, we see that the current in the LCR circuit will depend upon frequency. The current, therefore, reaches its maximum value when the impedance is minimum. This happens when XL = XC, corresponding to Z = R. The frequency ω at which this occurs is called resonant angular frequency. To find ω0, we use the condition XL = XC, from which we get
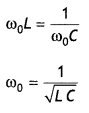
But ωo = 2 πfo, where fo is called resonance frequency. Therefore, the above equation becomes fo = \(\frac{1}{2 \pi} \frac{1}{\sqrt{L C}}\)
Question 8.
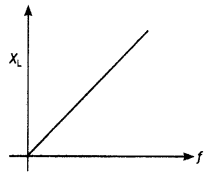
Explain the term ‘inductive reactance’. Show graphically the variation of an inductive reactance with the frequency of the applied alternating voltage.
An ac voltage E = Eo sin ωt is applied across a pure inductor of inductance L. Show mathematically that the current flowing through it lags behind the applied voltage by a phase angle of π/2.
Answer:
It is the opposition offered to the flow of current by a pure inductor.
Consider an ac circuit consisting of a pure Inductor connected to the terminaLs of an ac source. Let the Instantaneous value of the ac source be
V = Vm sin ωt ….(1)
Let VL be the instantaneous voltage drop across the inductor, then Kirchoff’s loop rule when applied to the circuit gives V + VL = 0
or
V – L\(\frac{di}{dt}\) = 0 …(2)
since VL = – L\(\frac{di}{dt}\)
Using equations (1) and (2) we have

Integrating the above equation we have

where \(\frac{V_{m}}{\omega L}\) = lm , ωL = 2πfL has the dimensions of resistance and is called the inductive reactance of the circuit. Using the trigonometric identity cos ωt = – sin (ωt – π/2) in equation (6) we have
lL =lm sin (ωt – π/2) …(7)
Comparing equation (1) with equation (7) we see that the current lags voltage by π/2 radian or 90°.
Question 9.
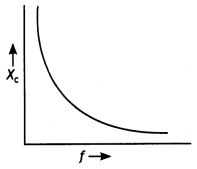
Explain the term ‘capacitive reactance’. Show graphically the variation of a capacitive reactance with the frequency of the applied alternating voltage.
An ac voltage E=Eo sin cot is applied across a pure capacitor of capacitance C. Show mathematically that the current flowing through it leads the applied voltage by a phase angle of π/2.
Answer:
It is the opposition offered to the flow of current by a pure capacitor.
Consider an ac circuit consisting of a capacitor connected to an ac source. Let the instantaneous value of emf be
V = Vm sin ωt …(1)
Let Vc be the instantaneous voltage drop across the capacitor, then by Kirchoff’s loop rule,
V – VC = 0
V = VC = Vm Sin ωt …(2)
But from the definition of capacitance, VC = Q / C or Q= VCC. Substituting for VC we have
Q = C Vm sin ωt …(3)
Differentiating equation (3) with respect to time we have,
\(\frac{d Q}{d t}=\frac{d}{d t}\)CVm sin ωt = ω C Vm cos ωt …(4)
But dQ/dt = lc, therefore the above equation becomes,
lC = ω C Vm cos ωt = lm cos ωt …(5)
where
lm = \(\frac{v_{m}}{\frac{1}{\omega C}}\)
Here the term \({\frac{1}{\omega C}}\) has the dimensions of resistance and is called the capacitive reactance of the circuit and ωCVm = lm.
Using the trigonometric identity cos ωt = sin (ωt + π/2), equation (5) can be written as
lC = lm sin (ωt + π/2) …..(6)
Comparing this expression with equation (1)
we see that the current is 90° (π/2) out of phase with the voltage across the capacitor. In other words, currently leads emf by 90°.
The graph of variation of XC with f is as shown.
Question 10.
Derive an expression for the impedance of a series LCR circuit connected to an ac supply of variable frequency. Plot a graph showing a variation of current with the frequency of the applied voltage. Explain briefly how the phenomenon of resonance in the circuit can be used in the tuning mechanism of a radio or a TV set. (CBSE Delhi 2011)
Answer:
The voltages across the various elements are drawn as shown in the figure below.
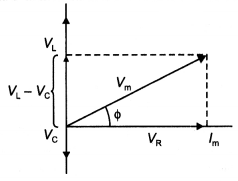
From the diagram, we observe that the vector sum of the voltage amplitudes VR, VL, and VC equals a phasor whose length is the maximum applied voltage Vm, where the phasor Vm makes an angle Φ with the current phasor lm. Since the voltage phasors, VL and VC are in opposite directions, a different phasor (VL – VC) is drawn which is perpendicular to the phasor VR.
Adding vectorially, we have
Vm = \(\sqrt{V_{R}^{2}+\left(V_{L}-V_{c}\right)^{2}}\)
= \(\sqrt{\left(l_{m} R\right)^{2}+\left(l_{m} X_{L}-l_{m} X_{c}\right)^{2}}\) …(1)
or
Vm = lm\(\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}\) …(2)
where XL = ω L and XC = 1/ω C, therefore we can express the maximum current as
lm = \(\frac{V_{m}}{\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}}\) …(3)
∴ lm = \(\frac{V_{m}}{Z}\)
The impedance Z of the circuit is defined as
Z = \(\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}\)
The graph is shown.

The graph is as shown.
The antenna of a radio accepts signals from many broadcasting stations. The signals picked up in the antenna act as a source in the tuning circuit of the radio, so the circuit can be driven at many frequencies. But to hear one particular radio station, we tune the radio. In tuning, we vary the capacitance of a capacitor in the tuning circuit such that the resonant frequency of the circuit becomes nearly equal to the frequency of the radio signal received. When this happens, the amplitude of the current with the frequency of the signal of the particular radio station in the circuit is maximum and that particular radio station is tuned in.
Question 11.
A device ‘X’ is connected to an ac source V = Vo sin ωt. The variation of voltage, current, and power in one cycle is shown in the following graph.
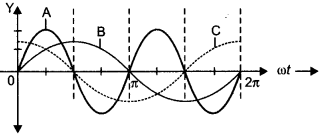
(a) Identify the device ‘X’.
Answer:
Capacitor
(b) Which of the curves A, B, and C represent the voltage, current, and power consumed in the circuit? Justify your answer.
Answer:
A: Power, B: Voltage, and C: Current.
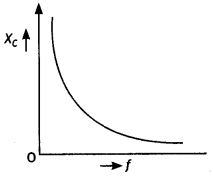
(c) How does its impedance vary with the frequency of the ac source? Show graphically.
Answer:
For a capacitor, Impedance is given by XC = 1 /ωC = 1 /2πfC. This is shown graphically as
(d) Obtain an expression for the current in the circuit and its phase relation with ac voltage. (CBSE AI 2017)
Answer:
Consider an ac circuit consisting of a capacitor connected to an ac source. Let the instantaneous value of emf be
V = Vo sin ωt …(1)
Let Vc be the instantaneous voltage drop across the capacitor, then by Kirchoff’s loop rule,
V – VC = 0
or
V = VC = Vo sin ωt …(2)
But from the definition of capacitance,
VC = Q / C
or
Q= VC C.
Substituting for Vc we have
Q = CVo sin ωt …(3)
Differentiating equation (3) with respect to time we have,
\(\frac{d Q}{d t}=\frac{d}{d t}\) CVo sin ω t = ω C Vo cos ω t …(4)
But dQ/dt = ic, therefore the above equation becomes,
ic = ω C Vo cos ω t = lo cos ω t …(5)
Here the term 1/ωc has the dimensions of resistance and is called the capacitive reactance of the circuit and ωCVm = lm. Using the trigonometric identity cos ω t = sin (ω t + π/2) equation (5) can be written as
ic = lo sin (ω t + π/2) …(6)
Comparing this expression with equation (1) we see that the current is 90° (π/2 ) out of phase with the voltage across the capacitor. In other words, currently leads emf by 90°.
Question 12.
A device X is connected across an ac source of voltage V = Vo sin ωt. The current through X is given as l = lo sin (ωt + π/2).
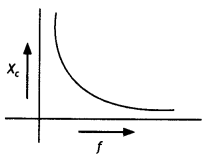
(a) Identify the device X and write the expression for Its reactance.
(b) Draw graphs showing the variation of voltage and current with time over one cycle of ac, for X.
(c) How does the reactance of device X vary with the frequency of the ac? Show this variation graphically.
(d) Draw the phasor diagram for the device X. (CBSE AI 2018, Delhi 2018)
Answer:
(a) X: capacitor
Reactance XC = 1 / ωC = 1 / 2πfC
(b) The graphs area as shown.
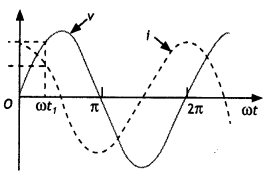
(c) Reactance of the capacitor varies in inverse proportion to the frequency. Therefore, the graph is as shown.
(d) The phasor diagram is as shown.
Question 13.
A resistor of 200 Ω and a capacitor of 15.0 μF is connected In series to a 220 V, 50 Hz ac source, (a) Calculate the current in the circuit; (b) Calculate the voltage (rms) across the resistor and the capacitor. Is the algebraic sum of these voltages more than the source voltage? If yes, resolve the paradox. (NCERT, CBSE Delhi 2004)
Answer:
Given R = 200 Ω, C= 15.0 μF = 15.0 × 10-6 F, V = 220 V, f = 50 Hz
(a) In order to calculate the current, we need the impedance of the
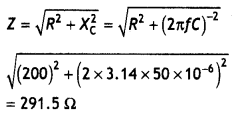
Therefore the current in the circuit is
l = \(\frac{V}{Z}=\frac{220}{291.5}\) = 0.7555 A
(b) Since the current is the same throughout the circuit we have
VR = IR = 0.755 × 200 = 151 V
VC = lXC = 0.755 × 212.3 = 160.3 V
The algebraic sum of the two voltages VR and Vc is 311.3 V which is more than the source voltage of 220 V. How to resolve this paradox? As you have learned in the text, the two voltages are not in the same phase. Therefore, they cannot be added like ordinary numbers. The two voltages are out of phase by ninety degrees. Therefore, the total of these voltages must be obtained using the Pythagorean theorem;
V = \(\sqrt{V_{R}^{2}+V_{C}^{2}}\) = 220 V
Thus if the phase difference between two voltages is properly taken into account, the total voltage across the resistor and the capacitor is equal to the voltage of the source.
Question 14.
Explain why the reactance offered by an inductor increases with the increasing frequency of an alternating voltage.
(NCERT Exemplar)
Answer:
An inductor opposes the flow of current through it by developing a back emf according to Lenz’s law. The induced voltage has a polarity so as to maintain the current at its present value. If the current is decreasing, the polarity of the induced emf will be so as to increase the current and vice versa. Since the induced emf is proportional to the rate of change of current, it will provide greater reactance to the flow of current if the rate of change is faster, i.e. if the frequency is higher. The reactance of an Inductor, therefore, is proportional to the frequency, being given by ωL.
Question 15.
(a) Prove that an Ideal capacitor in an ac circuit does not dissipate power.
Answer:
Consider an ac circuit consisting of a capacitor connected to an ac source. Let the instantaneous value of emf be
V = Vm sin ωt …(1)
Let Vc be the instantaneous voltage drop across the capacitor, then by Kirchoff’s loop rule,
V – VC = 0
V = VC = Vm Sin ωt …(2)
But from the definition of capacitance, VC = Q / C or Q= VCC. Substituting for Vc we have
Q = C Vm sin ωt …(3)
Differentiating equation (3) with respect to time we have,
\(\frac{d Q}{d t}=\frac{d}{d t}\)CV<sub>m</sub> sin ωt = ω C Vm cos ωt …(4)
But dQ/dt = lc, therefore the above equation becomes,
lC = ω C Vm cos ωt = lm cos ωt …(5)
where
lm = \(\frac{v_{m}}{\frac{1}{\omega C}}\)
Here the term \({\frac{1}{\omega C}}\) has the dimensions of resistance and is called the capacitive reactance of the circuit and ωCVm = lm.
Using the trigonometric identity cos ωt = sin (ωt + π/2), equation (5) can be written as
lC = lm sin (ωt + π/2) …..(6)
Comparing this expression with equation (1)
we see that the current is 90° (π/2) out of phase with the voltage across the capacitor. In other words, currently leads emf by 90°.
The graph of variation of XC with f is as shown.

Power in capacitive circuit P = Ev lv cos Φ. In pure captor 0 = 90° phase difference between voltage and current is π/2.
So power consumed in pure capdtor Pav = Ev lv cos 90° = 0.
(b) An ideal inductor of 200 mH, capacitor of 400 μF, and a resistor of 10 Ω are connected In series to an ac source of 50 V and variable frequency. Calculate
(i)the angular frequency at which maximum power dissipation occurs in the circuit and the corresponding value of effective current and
(ii) the value of Q factor in the circuit. (CBSE AI 2017C)
Answer:

Question 16.
(a) What is the principle of transformer?
(b) Explain how laminating the core of a transformer helps to reduce eddy current losses in it.
(c) Why the primary and secondary coils of a transformer are preferably wound on the same core?
Or
Show that In the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the Inductor Is constant In time. (CBSE Sample Paper 2018-19)
Answer:
(a) It works on the principle of mutual induction.
(b) In order to reduce the eddy current loss, the resistance of the core should be Increased. In a transformer, the core Is made up of thin sheets of steel, each lamination being insulated from others by a thin layer of varnish. As the laminations are thin, they will have relatively high resistance.
(c) This is done to maximize the sharing of magnetic flux and also so that magnetic flux per turn should become the same in both the primary and secondary coils.
Or
Let at any instant t, q be the charge on the capacitor and ‘l’ be the current through the inductor
q (t) = q0 cos ωt
i (t) = – q0 ω sin ωt
Energy stored in the capacitor at time t is
UE = \(\frac{1}{2} \frac{q^{2}}{c}=\frac{1}{2} \frac{q_{0}^{2}}{C}\) cos2 ωt
Energy stored in the inductor at time t is
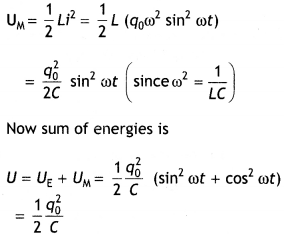
This sum is constant in time as q0 and C, both are time-independent.
Question 17.
Explain why the reactance provided by a capacitor to an alternating current decreases with increasing frequency. (NCERT Exemplar)
Answer:
A capacitor does not allow the flow of direct current through it as the resistance across the gap is infinite. When an alternating voltage is applied across the capacitor plates, the plates are alternately charged and discharged. The current through the capacitor is a result of this changing voltage (or charge). Thus, a capacitor will pass more current through it if the voltage is changing at a faster rate, i.e. if the frequency of the supply is higher. This implies that the reactance offered by a capacitor is less with increasing frequency; it is given by 1 /ωC.
Question 18.
(a) With the help of a labeled diagram, describe briefly the underlying principle and working of a step-up transformer.
(b) Write any two sources of energy loss in a transformer.
(c) A step-up transformer converts a low input voltage into a high output voltage. Does it violate the law of conservation of energy? Explain. (CBSE Delhi 2011)
Answer:
(a) The diagram is as shown.
It works on the principle of mutual induction i.e., whenever magnetic flux linked with a coil changes an emf is induced in the neighboring coil. In a step-up transformer, the number of turns in the secondary is more than that in the primary.
The ac source causes an alternating current in the primary, which sets up an alternating flux in the core; this induces an emf in each winding of the secondary, in accordance with Faraday’s law. The induced emf in the secondary gives rise to an alternating current in the secondary, and this delivers energy to the device to which the secondary is connected.
For step up : Ns> > Np
\(\frac{\varepsilon_{s}}{\varepsilon_{p}}=\frac{N_{s}}{N_{p}}\) and \(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\)
(b) Two major sources of energy loss in this device are:
- Heat produced due to production of eddy currents.
- Copper loss: heat produced in the copper coils
(c) No, a transformer does not change the power. Thus if a voltage increases current gets decreased such that the energy and power remain the same.
Question 19.
(a) Explain with the help of a labeled diagram, principle, and working of a transformer. Deduce the expression for its working formula.
Answer:
For diagram as shown.
- Principle: A transformer works on the basis of mutual induction.
- Working: In a 100% efficient transformer
εs ls = εp lp where l and lp, are the secondary and primary currents, therefore we have
\(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\) ….(1)
Now a 1oo % efficient transformer
we have
\(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}} \frac{\frac{d \phi}{d t}}{\frac{d \phi}{d t}}=\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}}\) …(2)
Therefore form (1) and (2) we have
\(\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\) = k
Efficiency of transformer = \(\frac{V_{s} I_{s}}{V_{p} I_{p}}\).
(b) Name any four causes of energy loss in an actual transformer. (CBSEAI 2013C)
Answer:
- Copper loss
- Iron loss
- Flux loss
- Hysteresis loss
Question 20.
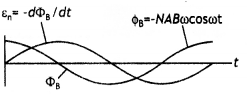
(a) Draw a schematic sketch of an ac generator describing its basic elements. State briefly its working principle. Show a plot of the variation of (i) Magnetic flux and alternating emf versus time generated by a loop of wire rotating in a magnetic field,
Answer:
A schematic sketch is as shown.
Working principle: Electromagnetic induction.
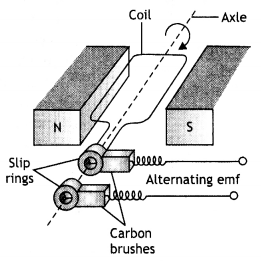
The graphs are as shown.
(b) Why is a choke coil needed in the use of fluorescent tubes with ac mains? (CBSE Delhi 2014)
Answer:
It is used to regulate current with minimum loss of energy.
Question 21.
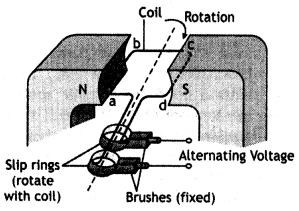
(a) Draw a labeled diagram of the AC generator. Derive the expression for the instantaneous value of the emf induced in the coil.
Answer:
It is based on the principle of electromagnetic induction. When a coil is rotated about an axis perpendicular to the direction of the uniform magnetic field, an induced emf is produced across it.
Working: The working of the ac generator can be understood with the help of the various positions of the armature as shown in the figure below.
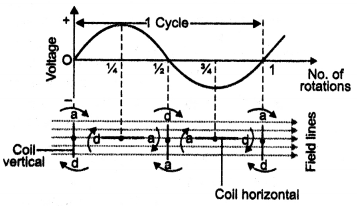
Suppose at time t = 0, the plane of the loop is perpendicular to B. As the loop rotates from position t = 0 to position t T/2, the Induced emf changes from zero to maximum value and then becomes zero again as shown in the diagram For angles 0° and 1800 the instantaneous rate of magnetic flux is zero, hence induced emf Is zero.
As the Loop moves from position t = T/2 to position t = T, the emf again changes from zero to the maximum value and then again becomes zero. But this time it reverses Its direction. For angles 90° and 270° maximum magnetic flux are linked with the coil hence the emf is a maximum. Thus the output of the ac generator varies sinusoidally with time. The Induced emf does not depend upon the shape of the Loop but depends only upon the area of the loop.
The emf generated Is given by the expression ε = nBAω Sin ωt, where ω is the speed of rotation of the coil
(b) A circular coil of cross-sectional area 200 cm2 and 20 turns is rotated about the vertical diameter with an angular speed of 50 rad s-1 in a uniform magnetic field of magnitude 3.O × 10-2 T. Calculate the maximum value of the current in the coil. (CBSE Delhi 2017)
Answer:
Given A = 200 cm2, ω = 50 rad s-1, n = 20
S = 3 × 10-2 T, εo = ?,
Using the relation ε0 = nBAω
= 20 × 3 × 10-2 × 200 × 10-4 × 50 = 0.6 V
Question 22.
Draw a labeled diagram of a step-up transformer. Obtain the ratio of secondary to primary voltage in terms of the number of turns and currents in the two coils.
A power transmission line feeds input power at 2200 V to a step-down transformer with its primary windings having 3000 turns. Find the number of turns in the secondary to get the power output at 220 V. (CBSE Delhi 2017)
Answer:
(a) The diagram is as shown.

It works on the principle of mutual induction i.e., whenever magnetic flux linked with a coil changes an emf is induced in the neighboring coil. In a step-up transformer, the number of turns in the secondary is more than that in the primary.
The ac source causes an alternating current in the primary, which sets up an alternating flux in the core; this induces an emf in each winding of the secondary, in accordance with Faraday’s law. The induced emf in the secondary gives rise to an alternating current in the secondary, and this delivers energy to the device to which the secondary is connected.
For step up : Ns > Np
\(\frac{\varepsilon_{s}}{\varepsilon_{p}}=\frac{N_{s}}{N_{p}}\) and \(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\).
Principle – It works on the principle of electromagnetic induction. When the current in one circuit changes, an induced current is set up in the neighboring circuit.
(b) Ns = ?, Np = 3000
Ep = 2200 V, Es = 220 V
Since, Es/Ep = Ns/Np
220/2200 = Ns/3000
Ns = 300
Question 23.
(a) State the principle of working of a transformer.
Answer:
It works on the principle of mutual inductance i.e. whenever the magnetic flux Linked in a coil changes an induced emf Is produced in the neighboring coil.
(b) Define the efficiency of a transformer.
Answer:
It is the ratio of the output power to the input power.
(c) State any two factors that reduce the efficiency of a transformer.
Answer:
Copper Loss, flux Loss
(d) Calculate the current drawn by the primary of a 90% efficient transformer which steps down 220 V to 22 V If the output resistance Is 440 Ω. (CBSFAI 2018 C)
Answer:
Given η = 90%, Vp = 22OV, Vs = 22V, Ro = 440 W
Now ls = Vs/R = 22/440 = 0.05 A
Also η = \(\frac{P_{0}}{P_{1}}=\frac{V_{s} l_{s}}{V_{p} l_{p}}\) , therefore we have
\(\frac{90}{100}=\frac{22 \times 0.05}{220 \times l_{\mathrm{p}}}\)
or
lp = 0.0056 A
Question 24.
Draw an arrangement for winding of primary and secondary coil In a transformer with two coils on a separate limb of the core.
State the underlying principle of a transformer. Deduce the expression for the ratio of secondary voltage to the primary voltage In terms of the ratio of the number of turns of the primary and secondary winding. For an ideal transformer, obtain the ratio of primary and secondary currents In terms of the ratio al the voltages in the secondary and primary voltages. Write any two reasons for the energy losses which occur In actual transformers, (CBSE Dei hi 2016C)
Answer:
Principle: When an alternating voltage is applied to the primary, the resulting current produces an alternating magnetic flux which Links the secondary and Induces an emf in it.
Induced emf, or voltage, in the secondary, with ‘Ns‘ number of turns,
εs = – Ns \(\frac{d \phi}{d t}\)
Back emf In the primary with Np turns,
εp = – Np \(\frac{d \phi}{d t}\)
Since εs = Vs and εp = Vp
Therefore we have
\(\frac{V_{p}}{V_{s}}=\frac{N_{p}}{N_{s}}\)
For an ideal transformer,
Input power = output power
Therefore
lpVp = lsVs
Or
\(\frac{V_{p}}{V_{s}}=\frac{l_{s}}{l_{p}}\)
(a) Heat energy Loss.
(b) Humming effect Loss.
Question 25.
A pure inductor is connected across an ac source. Show mathematically that the current in it lags behind the applied emf by a phase angle of π/2. What is its inductive reactance? Draw a graph showing the variation of an inductive reactance with the frequency of the ac source.
Answer:
Consider an ac circuit consisting of a pure Inductor connected to the terminaLs of an ac source. Let the Instantaneous value of the ac source be
V = Vm sin ωt ….(1)

Let VL be the instantaneous voltage drop across the inductor, then Kirchoff’s loop rule when applied to the circuit gives V + VL = 0
or
V – L\(\frac{di}{dt}\) = 0 …(2)
since VL = – L\(\frac{di}{dt}\)
Using equations (1) and (2) we have

Integrating the above equation we have

where \(\frac{V_{m}}{\omega L}\) = lm , ωL = 2πfL has the dimensions of resistance and is called the inductive reactance of the circuit. Using the trigonometric identity cos ωt = – sin (ωt – π/2) in equation (6) we have
lL =lm sin (ωt – π/2) …(7)
Comparing equation (1) with equation (7) we see that the current lags voltage by π/2 radian or 90°.

Question 26.
An alternating emf Is applied across a capacitor. Show mathematically that the current leads the emf by a phase angle π/2, What Is its capacitive reactance? Draw a graph showing the variation of a capacitive reactance with the frequency of the ac source.
Answer:
Consider an ac circuit consisting of a capacitor connected to an ac source. Let the instantaneous value of emf be
V = Vm sin ωt …(1)
Let Vc be the instantaneous voltage drop across the capacitor, then by Kirchoff’s loop rule,
V – VC = 0
V = VC = Vm Sin ωt …(2)
But from the definition of capacitance, VC = Q / C or Q= VCC. Substituting for VC we have
Q = C Vm sin ωt …(3)
Differentiating equation (3) with respect to time we have,
\(\frac{d Q}{d t}=\frac{d}{d t}\)CVm sin ωt = ω C Vm cos ωt …(4)
But dQ/dt = lC, therefore the above equation becomes,
lC = ω C Vm cos ωt = lm cos ωt …(5)
where
lm = \(\frac{v_{m}}{\frac{1}{\omega C}}\)
Here the term \({\frac{1}{\omega C}}\) has the dimensions of resistance and is called the capacitive reactance of the circuit and ωCVm = lm.
Using the trigonometric identity cos ωt = sin (ωt + π/2), equation (5) can be written as
lC = lm sin (ωt + π/2) …..(6)
Comparing this expression with equation (1)
we see that the current is 90° (π/2) out of phase with the voltage across the capacitor. In other words, currently leads emf by 90°.
The graph of variation of XC with f is as shown.

Question 27.
(a) In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with the frequency of the ac source.
Answer:
The voltages across the various elements are drawn as shown in the figure below.

From the diagram, we observe that the vector sum of the voltage amplitudes VR, VL, and VC equals a phasor whose length is the maximum applied voltage Vm, where the phasor Vm makes an angle Φ with the current phasor lm. Since the voltage phasors, VLand VC is in opposite directions, a different phasor (VL – VC) is drawn which is perpendicular to the phasor VR.
Adding vectorially, we have
Vm = \(\sqrt{V_{R}^{2}+\left(V_{L}-V_{c}\right)^{2}}\)
= \(\sqrt{\left(l_{m} R\right)^{2}+\left(l_{m} X_{L}-l_{m} X_{c}\right)^{2}}\) …(1)
or
Vm = lm\(\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}\) …(2)
where XL = ω L and XC = 1/ω C, therefore we can express the maximum current as
lm = \(\frac{V_{m}}{\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}}\) …(3)
∴ lm = \(\frac{V_{m}}{Z}\)
The impedance Z of the circuit is defined as
Z = \(\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}\)
The graph is shown.

(b) What is the phase difference between the voltages across the inductor and the capacitor at resonance in the LCR circuit?
Answer:
The phase difference between the voltage across the inductor and the capacitor at resonance is 180°.
(c) When an inductor is connected to a 200V dc voltage, a current of 1A flows through it. When the same inductor is connected to a 200V, 50 Hz ac source, only 0.5A current flows. Explain why? Also, calculate the self-inductance of the inductor. (CBSE Delhi 2019)
Answer:
Inductor will offer an additional impedance to ac due to its self-inductance.
Now R = \(\frac{V_{\text {rms }}}{l_{\text {rms }}}=\frac{200}{1}\) = 200 Ω
The impedance of the inductor
Z = \(\frac{V_{\mathrm{rms}}}{l_{\mathrm{rms}}}=\frac{200}{0.5}\) = 400 Ω
Now Z = \(\sqrt{R^{2}+X_{L}^{2}}\) , therefore
XL2 = Z2 – R2
XL = \(\left(\sqrt{(400)^{2}-(200)^{2}}\right)\) = 346.4 Ω
Hence inductance (L) is
L = \(\frac{X_{L}}{\omega}=\frac{346.4}{2 \times 3.14 \times 50}\) = 6.2 H
Question 28.
(a) Obtain the expression for the average power dissipated in a series LCR circuit driven by an ac source of voltage V = Vm sin ωt supplying the current i = im sin (ωt + Φ).
Answer:
Average Power dissipated in a series LCR circuit
Given V = Vm sin tot
And l = im sin (ωt + Φ)
Instantaneous Power
P = Vi
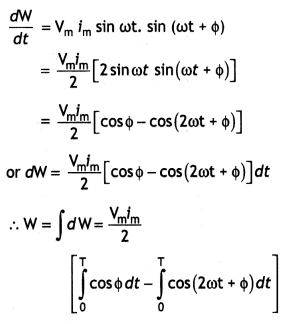
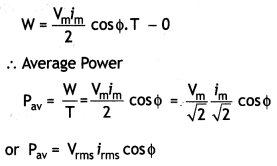
(b) Define the terms:
(i) Wattless current, and
Answer:
Wattles’s current: If the average power consumed due to the flow of current in a circuit is zero, the current is said to be wattless.
(ii) Q – a factor of LCR circuit.
Answer:
Q-factor of an LCR Circuit: Q-factor of the LCR circuit is the ratio of the potential difference across inductance (or capacitance) at resonance to the applied voltage.
Question 29.
Distinguish between the terms reactance and impedance of an ac circuit. Prove that an ideal capacitor connected to an ac source does not dissipate power.
| S.No. Reactance | Impedance |
| 1. It is the opposition offered by a pure inductor or a pure capacitor or both to the flow of ac. | 1. It is the opposition offered by LR or CR or LCR circuit to the flow of ac |
| 2. It depends upon the frequency of ac. | 2. It depends upon the frequency of ac. |
| 3. It can be inductive or capacitive. | 3. It can be inductive, capacitive, or resistive. |
| 4. It can be zero. | 4. It can never be zero. |
Consider an ac circuit consisting of a capacitor connected to an ac source. Let the instantaneous value of emf be
V = Vm sin ωt …(1)
Let VC be the instantaneous voltage drop across the capacitor, then by Kirchoff’s loop rule,
V – VC = 0
V = VC = Vm Sin ωt …(2)
But from the definition of capacitance, VC = Q / C or Q= VCC. Substituting for Vc we have
Q = C Vm sin ωt …(3)
Differentiating equation (3) with respect to time we have,
\(\frac{d Q}{d t}=\frac{d}{d t}\)CVm sin ωt = ω C Vm cos ωt …(4)
But dQ/dt = lc, therefore the above equation becomes,
lC = ω C Vm cos ωt = lm cos ωt …(5)
where
lm = \(\frac{v_{m}}{\frac{1}{\omega C}}\)
Here the term \({\frac{1}{\omega C}}\) has the dimensions of resistance and is called the capacitive reactance of the circuit and ωCVm = lm.
Using the trigonometric identity cos ωt = sin (ωt + π/2), equation (5) can be written as
lC = lm sin (ωt + π/2) …..(6)
Comparing this expression with equation (1)
we see that the current is 90° (π/2) out of phase with the voltage across the capacitor. In other words, current leads emf by 90°.
The graph of variation of Xc with f is as shown.

Question 30.
Define the term root mean square (rms) value of ac. Derive the relation between rms value and the peak value of ac.
Answer:
It is that value of steady current (dc) which when passed through a resistor in a given time produces the same heat as is produced by the ac. when passed through the same resistor for the same time. It is abbreviated as rms value of current. It is denoted by lrms.
Consider an ac source. Let the instantaneous value of current be represented by the equation
i = lm sin ωt
Let this current pass through a resistor of resistance R. Therefore in a small-time dt, the amount of heat produced in the resistor is
dH = i2 R dt
The total amount of heat produced in one complete cycle of ac is given by
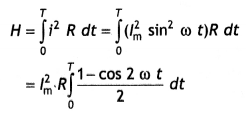
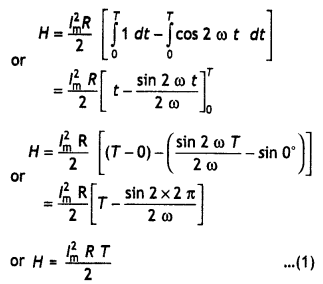
Let lrms be the virtual value of ac, then the amount of heat produced in the same resistor of resistance R, in the same time T is
H = lrms2RT …(2)
Therefore from equations (1) and (2) we have
lrms = \(\frac{l_{m}}{\sqrt{2}}\) = 0.707 lm
Question 31.
(a) Prove that the current flowing through an Ideal Inductor connected across a.c. source lags the voltage In phase by nil.
Answer:
(a) Consider an ac circuit consisting of a pure inductor connected to the terminals of an ac source. Let the instantaneous value of the ac source be
V = Vm sin ω t …(1)
Let VL be the instantaneous voltage drop across the inductor, then Kirchoff’s loop rule when applied to the circuit gives V + VL = 0
or
V – L\(\frac{di}{dt}\) = 0 …(2)
since VL = – L \(\frac{di}{dt}\)
Using equations (1) and (2) we have
L\(\frac{di}{dt}\) = Vm sin ω t …(3)
or
di = \(\frac{V_{m}}{L}\) sin ω t dt …(4)
Integrating the above equation we have
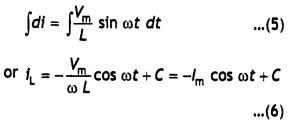
C = 0, over a period of cycle
\(\frac{V_{\mathrm{m}}}{\omega L}\) = lm, ωL = 2πfL has the dimensions of resistance and is called the inductive reactance of the circuit. Using the trigonometric identity
cos ω t = – sin (ωt – π/2) in equation (6) we have
lL = lm sin (ωt – π/2) …(7)
Comparing equation (1) with equation (7) clearly shows that the current lags voltage by π/2 radian or 90°.
(b) An inductor of self-inductance 100 mH and a bulb are connected in series with a.c. source of rms voltage 10 V, 50 Hz. It is found that the effective voltage of the circuit leads the current in phase by π/4. Calculate the resistance of the bulb used and average power dissipated in the circuit, if a current of 1 A flows in the circuit. (CBSE Delhi 2017C)
Answer:
(b) V= 10 V, f = 50 Hz, l = 1.0 A, Φ = π/4, R = ?, L = 100mH = 0.1 H
Now Z = V/l = 10/1.0 = 10 ohm
Also Z = \(\sqrt{R^{2}+X_{L}^{2}}\) = 10
Now cos Φ = \(\frac{R}{Z}\)
or
Therefore, R = cos Φ × Z
Or
R = cos π/4 × 10 = 7 ohm
Power dissipated
Pav = lrms Vrms cos Φ = \(\frac{V_{m}^{2}}{Z}\) × cos Φ
0r
Pav = \(\frac{(10)^{2}}{10}\) × 0.707 = 7.07 W
Question 32.
(a) Draw graphs showing the variations of inductive reactance and capacitive reactance with the frequency of the applied ac source.
(b) Draw the phasor diagram for a series RC circuit connected to an ac source.
(c) An alternating voltage of 220 V is applied across a device X, a current of 0.25 A flows, which lag behind the applied voltage In phase by \(\frac{π}{2}\) radian. If the same voltage is applied across another device Y, the same current flows but now it is in phase with the applied voltage.
(i) Name the devices X and Y.
(ii) Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y. (CBSEAI 2018C)
Or
(a) State the principle of working of a transformer.
(b) Define the efficiency of a transformer.
(c) State any two factors that reduce the efficiency of a transformer.
(d) Calculate the current drawn by the primary of a 90% efficient transformer which steps down 220 V to 22 V, if the output resistance is 440 Ω.
Answer:
(a) The two graphs are as shown.
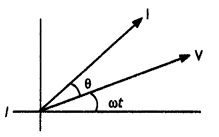
(b) (The current leads the voltage by an angle 0 where 0 < θ < \(\frac{π}{2}\).) The required phasor diagram is as shown.
Here θ = tan-1 \(\frac{1}{ωCR}\)
(c) In device X:
Current lags behind the voltage by \(\frac{π}{2}\)
∴ X is an inductor.
In device Y:
Current is in phase with the applied voltage
∴ X is a resistor.
We are given that 0.25 = \(\frac{220}{X_{L}}\)
or
XL = \(\frac{220}{0.25}\) Ω = 880 Ω
Also 0.25 = 0.25 = \(\frac{220}{X_{R}}\)
∴ XR = \(\frac{220}{0.25}\) Ω = 880 Ω
For the series combination of X and Y, Equivalent impedance
= \(\sqrt{X_{L}^{2}+X_{R}^{2}}\) = (880\(\sqrt{2}\) Ω
∴ Current flowing = \(\frac{220}{880 \sqrt{2}}\) A = 0.177 A
Or
(a) A transformer works on the principle of mutual induction. (Alternatively, an emf is induced in the secondary coil when the magnetic flux linked with it changes with time due to changing magnetic flux linked with the primary coil).
(b) The efficiency of a transformer equals the ratio of the output power to the input power.
Efficiency = \(\frac{\text { output power }}{\text { input power }}\)
or
Efficiency = \(\frac{V_{S} I_{S}}{V_{P} I_{p}}\)
(c)
- Eddy current Losses
- route heat Losses
- hysteresis Losses
- magnetic flux leakage Losses
We have
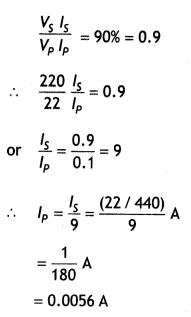
Question 33.
(a) Draw a schematic diagram of a step-up transformer. Explain its working principle. Assuming the transformer to be 100% efficient, obtain the relation for
(i) the current in the secondary in terms of the current in the primary, and
(ii) the number of turns in the primary and secondary windings.
(b) Mention two Important energy losses in actual transformers and state how these can be minimized. (CBSE Delhi 2011C)
Answer:
(a) For diagram as shown.

- Principle: A transformer works on the basis of mutual induction.
- Working: In a 100% efficient transformer
εs ls = εp lp where l and lp are the secondary and primary currents, therefore we have
\(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\) ….(1)
Now a 1oo % efficient transformer
we have
\(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}} \frac{\frac{d \phi}{d t}}{\frac{d \phi}{d t}}=\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}}\) …(2)
Therefore form (1) and (2) we have
\(\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\) = k
Efficiency of transformer = \(\frac{V_{s} I_{s}}{V_{p} I_{p}}\)
(b) The two important energy losses in actual transformers are:
- Iron losses in the core of the transformer.
- Loss of energy in the primary and secondary due to Joule heating. The iron losses due to eddy currents are minimized by laminating the iron core.
Question 34.
(a) Draw the diagram of a device that is used to decrease high ac voltage into a low ac voltage and state its working principle. Write four sources of energy loss in this device.
Answer:
The labeled diagram is as shown.
It works on the principle of mutual induction, i.e. whenever magnetic flux linked with a coil changes, an emf is induced in the neighboring coil.
The possible causes of energy losses in transformers are:
- Flux leakage
- Copper loss
- Eddy currents
- Hysteresis loss
(b) A small town with a demand of 1200kW of electric power at 220 V is situated 20 km away from an electric plant generating power at 440V. The resistance of the two wirelines carrying power is 0.5 Ω per km. The town gets the power from the line through a 4000 – 220V step-down transformer at a sub-station in the town. Estimate the line power loss in the form of heat. (CBSE Delhi 2019)
Answer:
Total resistance of the line = length × resistance per unit length = 40 km × 0.5 = 20 Ω
Current flowing in the line l = P/V
= 1200 × 103 /4000 = 300 A
Power loss = l2R = (300)2 × 20 = 1800 kW
Question 35.
(a) State the principle of an ac generator and explain its working with the help of a labeled diagram. Obtain the expression for the emf induced in a coil having N turns each of cross-sectional area A, rotating with a constant angular speed ‘co’ in a magnetic field B, directed perpendicular to the axis of rotation.
Answer:
For principle and diagram


Suppose at time t = 0, the plane of the loop is perpendicular to B. As the loop rotates from position t = 0 to position t T/2, the Induced emf changes from zero to maximum value and then becomes zero again as shown in the diagram For angles 0° and 1800 the instantaneous rate of magnetic flux is zero, hence induced emf Is zero. As the Loop moves from position t = T/2 to position t = T, the emf again changes from zero to the maximum value and then again becomes zero. But this time it reverses Its direction. For angles 90° and 270° maximum magnetic flux are linked with the coil hence the emf is a maximum. Thus the output of the ac generator varies sinusoidally with time. The Induced emf does not depend upon the shape of the Loop but depends only upon the area of the loop.
The emf generated Is given by the expression ε = nBAω Sin ωt, where ω is the speed of rotation of the coiL.
(b) An airplane is flying horizontally from west to east with a velocity of 900 km h-1. Calculate the potential difference developed between the ends of its wings having a span of 20 m. The horizontal component of the Earth’s magnetic field is 5 × 10-4 T and the angle of dip is 30°. (CBSEAI 2018, Delhi 2018)
Answer:
Potential difference developed between the ends of the wings
ε = BLv
Given Velocity V = 900 km h-1 = 250 m s-1
Wing span (L1) = 20 m
Vertical component of Earth’s magnetic field
Bv = BH tan δ = 5 × 10-4 (tan 30°) T
∴ Potential difference
= 5 × 10-4 (tan 30°) × 20 × 250 = 1.44 V
Question 36.
Explain, with the help of a diagram, the principle and working of an ac generator. Write the expression for the emf generated in the coil in terms of its speed of rotation.
Answer:
It is based on the principle of electromagnetic induction. When a coil is rotated about an axis perpendicular to the direction of a uniform magnetic field, an induced emf is produced across it.
Working: The working of the ac generator can be understood with the help of the various positions of the armature as shown in figure below.


Suppose at time t = 0, the plane of the loop is perpendicular to B. As the loop rotates from position t = 0 to position t T/2, the Induced emf changes from zero to maximum value and then becomes zero again as shown in the diagram For angles 0° and 1800 the instantaneous rate of magnetic flux is zero, hence induced emf Is zero. As the Loop moves from position t = T/2 to position t = T, the emf again changes from zero to a maximum value and then again becomes zero. But this time it reverses Its direction. For angles 90° and 270° maximum magnetic flux are linked with the coil hence the emf is a maximum. Thus the output of the ac generator varies sinusoidally with time. The Induced emf does not depend upon the shape of the Loop but depends only upon the area of the loop.
The emf generated Is given by the expression ε = nBAω Sin ωt, where ω is the speed of rotation of the coiL.
Numerical Problems:
Formulae for solving numerical problems
- Capacitive reactance XC = \(\frac{1}{\omega C}=\frac{1}{2 \pi f C}\)
- Inductive reactance XL = ωL = 2πfL
- When ac flows through an LR circuit then,
Z = \(\sqrt{R^{2}+X_{L}^{2}}\) and tan Φ = \(\frac{X_{L}}{R}=\frac{\omega L}{R}\) - When ac flows through a CR circuit then,
Z = \(\sqrt{R^{2}+X_{C}^{2}}\) and tan Φ = \(\frac{X_{c}}{R}=\frac{1}{\omega C R}\) - For a senes LCR circuit driven by voltage V = Vm sin ωt, the current is given by
l = lm sin (ωt + Φ) where
lm = \(\frac{V_{m}}{\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}}\) - The impedance of this circuit is given by
Z = \(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\)
\(\frac{V_{s}}{V_{p}}=\frac{N_{s}}{N_{p}}=\frac{I_{p}}{I_{s}}\) = k.
Question 1.
The figure shows how the reactance of an Inductor varies with frequency. (a) Calculate the value of the Inductance of the Inductor using Information given In the graph. (b) If this Inductor is connected In senes to a resistor of 8 ohms, find what would be the impedance at 300 Hz.
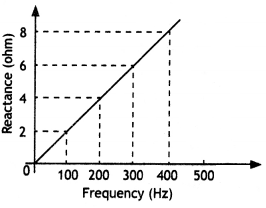
Answer:
(a) We know that XL = 2πfL or L = \(\frac{X_{L}}{2 \pi f}\).
Now slope of the graph is
\(\frac{X_{L}}{f}=\frac{8-6}{400-300}=\frac{2}{100}\) = 0.02
Therefore L is L = \(\frac{X_{L}}{2 \pi f}=\frac{0.02}{2 \times 3.14}\) = 0.0032 H
(b) NowR = 8 ohm, f = 300 Hz, Z = ?
Now Z = \(\sqrt{R^{2}+X_{L}^{2}}\) . Therefore we have
Z = \(\sqrt{R^{2}+X_{L}^{2}}\) = \(\sqrt{(8)^{2}+(6)^{2}}\) = 10 Ω
Question 2.
A 25.0 μF capacitor, a 0.10-henry Inductor, and a 25.0-ohm resistor are connected in series with an ac source whose emf is E= 310 s. In 314 t (i) what is the frequency of the .mf? (ii) Calculate (a) the reactance of the circuit (b) the Impedance of the circuit and (C) the current in the circuit.
Answer:
Given C = 25.0 μF, L = 0.10 henry, R = 25.0 ohm, Eo = 310V,
Comparing with the equation E = Eo sin ωt,
we have
(i) ω = 314 or f = 50 Hz

Question 3.
A sinusoidal voltage V = 200 sin 314 t Is applied to a resistor of 10 ohms. Calculate (i) rms value of current (ii) rms value of voltage and (iii) power dissipated as heat in watt.
Answer:
Vo = 200 V, ω = 314 rads-1 , Vrms = ?, lrms = ?, P = ?
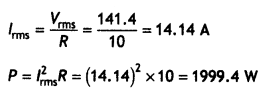
Question 4.
Find the inductance of the inductor used in series with a bulb of resistance 10 ohms connected to an ac source of 80 V, 50 Hz. The power factor of the circuit is 0.5. Also, calculate the power dissipation in the circuit.
Answer:
Given R = 10 ohm, V = 80 Hz, f = 50 Hz, cos Φ = 0.5 , L = ?, P = ?
Using the formula
cos Φ = \(\frac{R}{\sqrt{R^{2}+X_{L}^{2}}}\)
or
0.25(R2 + X2) = R2
Or
O.25XL2 = O.75R2
or
XL = 17.32 ohm
Now using XL = 2πfL we have
L = \(\frac{X_{L}}{2 \pi f}=\frac{17.32}{2 \times 3.14 \times 50}\) = 0.055 H
Now Z = \(\sqrt{R^{2}+X_{L}^{2}}\)
= \(\sqrt{(10)^{2}+(17.32)^{2}}\) = 20 Ω
Now Pav = lrms Vrms cos Φ = \(\frac{V_{m}^{2}}{Z}\) × cos Φ
or
Pav = \(\frac{(80)^{2}}{2 \times 20}\) × 0.5 = 160 W
Question 5.
When an alternating voltage of 220 V is applied across a device X, a current of 0.5 A flows through the circuit and Is in phase with the applied voltage. When the same voltage is applied across a device Y, the same current again flows through it, but it leads the voltage by π/2. If element ‘X’ is a pure resistor of 100 ohms,
(a) name the circuit element ‘Y’ and
Answer:
The element Y is a capacitor.
(b) calculate the rms value of current, if rms value of voltage is 141 V.
Answer:
The value of Xc is obtained as below
XC = \(\frac{V}{I}=\frac{220}{0.5}\) = 440 ohm
Therefore impedance of the circuit
Z = \(\sqrt{R^{2}+X_{C}^{2}}=\sqrt{(100)^{2}+(440)^{2}}\) = 451.2 ohm
Therefore rms value of current V 141
l = \(\frac{V_{r m s}}{Z}=\frac{141}{451.2}\) = 0.3125 A
Question 6.
When an alternating voltage of 220 V is applied across a device X, a current of 0. 5 A flows through the circuit and is in phase with the applied voltage. When the same voltage is applied across a device V, the same current again flows through it, but it lags the voltage by π/2.
(a) Name the devices X and Y.
Answer:
The element X is a resistor and Y is an inductor.
(b) Calculate the current flowing through the circuit when the same voltage is applied across the series combination of the two devices X and Y.
Answer:
Now both R and XL are the same and are given by
R = XL = \(\frac{220}{0.5}\) = 440 ohm
Hence impedance of the circuit
Z = \(\sqrt{R^{2}+X_{L}^{2}}\)
= \(\sqrt{(440)^{2}+(440)^{2}}\)
= 622.2 ohm
Therefore current flowing through the circuit is
l = \(\frac{V}{Z}\) = \(\frac{220}{622.2}\) = 0.353 A
Question 7.
A 15.0 μF capacitor Is connected to a 220 V, 50 Hz source. Find the capacitive reactance and the current (rms and peak) In the circuit. If the frequency Is doubled, what happens to the capacitive reactance and the current?
Answer:
Given C= 15.0 μF= 15 × 10-6 F, V= 220 V,
f = 50 HZ, XC = ? lm = ?
The capacitive reactance is
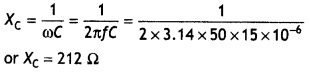
Now lrms = \(\frac{V_{r m s}}{X_{c}}=\frac{220}{212}\) = 1.04 A
Peak value of current
lm = \(\sqrt{2}\) × lrms = 1.4.1 × 1.04 = 1.47 A
This current oscillates between + 1.47A and – 1.47 A, and is ahead of the voltage by π/2.
If the frequency is doubled, the capacitive reactance is halved and consequently, the current is doubled.
Question 8.
A sinusoidal voltage of peak value 283 V and frequency 50 Hz is applied to a series LCR circuit in which R = 3 Ω, L = 25.48 mH and C = 796 μF. Find
(a) the impedance of the circuit;
(b) the phase difference between the voltage across the source and the current;
(c) the power dissipated in the circuit; and
(d) the power factor.
Answer:
Given Vm = 283 V, f = 50 Hz, R = 3 Ω
L = 25.48 mH, and C = 796 μF.
(a) To find the impedance of the circuit, we first calculate XL and Xc
XL = 2πfL = 2 × 3.14 × 50 × 25.48 × 10-3 = 8 Ω
XC = \(\frac{1}{2πfC}\)
= \(\frac{1}{2 \times 3.14 \times 50 \times 796 \times 10^{-6}}\) = 4 Ω
Therefore impedance of the circuit is
Z = \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{C}\right)^{2}}\)
= \(\sqrt{3^{2}+(8-4)^{2}}\)
= 5 Ω
(b) Phase difference
Φ = tan-1\(\frac{X_{L}-X_{c}}{R}\) = tan-1 \(\frac{8-4}{3}\) = 53.1°
Since Φ is positive therefore voltage leads current by the above phase.
(c) The power dissipated in the circuit is
P = \(\frac{V_{\mathrm{rms}}^{2}}{Z}=\frac{V_{\mathrm{m}}^{2}}{2 \mathrm{Z}}=\frac{(283)^{2}}{2 \times 5}\) = 8008.9 W
(d) power factor = cos Φ = cos 53.1° = 0.6
Question 9.
A capacitor and a resistor are connected in series with an ac source. If the potential difference across the C, R is 120 V and 90 V respectively, and if rms current of the circuit is 3 A, calculate the (i) impedance and (ii) power factor of the circuit.
Answer:
Given VC = 120 V, VR = 90 V, f = 3 A. and R = 90/3 = 30 ohm ,
Effective voltage in the circuit
V = \(\sqrt{V_{C}^{2}+V_{R}^{2}}=\sqrt{(120)^{2}+(90)^{2}}\)= 150 V .
(i) Therefore impedance of the circuit
Z = \(\frac{V}{l}=\frac{150}{3}\) = 50 Ω.
(ii) Now power factor of the circuit is
cos Φ = \(\frac{R}{Z}=\frac{30}{50}\) = 0.6
Question 10.
An inductor 200 mH, a capacitor C, and a resistor 10 ohm are connected in series with 100 V, 50 Hz ac source. If the current and the voltage are in phase with each other, calculate the capacitance of the capacitor.
Answer:
When current and voltage are in phase then XL = XC
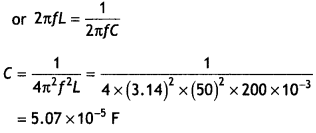
Question 11.
An ac voltage of 100V, 50 Hz is connected across a 20-ohm resistor and 2 mH inductors in series.
Calculate (i) impedance of the circuit, and
(ii) rms current in the circuit. (NCERT)
Answer:
Given, V = 100 V, f = 50 Hz, R = 20 ohm, L = 2 mH = 2 × 10-3 H, Z = ?, lrms = ?
Using the relation
(a) Z = \(\sqrt{(R)^{2}+\left(X_{L}\right)^{2}}=\sqrt{(R)^{2}+(2 \pi f L)^{2}}\)
Z = \(\sqrt{(20)^{2}+\left(2 \times 3.14 \times 50 \times 2 \times 10^{-3}\right)^{2}}\)
Z = 20 ohm
(b) lrms= V/Z= 100/20 = 5 A
Question 12.
A light bulb is rated at 100 W for a 220 V supply. Find (a) the resistance of the. bulb; (b) the peak voltage of the source; and (c) the rms current through the bulb. (NCERT)
Answer:
(a) We are given P = 100 W and V = 220 V.
The resistance of the bulb is
R = \(\frac{V^{2}}{P}=\frac{(220)^{2}}{100}\) = 484 Ω
(b) The peak voltage of the source is
Vm = \(\sqrt{2}\)V = \(\sqrt{2}\) × 220 = 311V
(c) Since P = I V, therefore l = P/V= 100/220 = 0.45 A
Question 13.
A pure Inductor of 25.0 mH is connected to a source of 220 V. Find the inductive reactance and rms current in the circuit if the frequency of the source is 50 Hz. (NCERT)
Answer:
The inductive reactance,
XL = 2 πf L = 2 × 3.14 × 50 × 25 × 10-3 Ω
= 7.85 ohm
The rms current in the circuit is
l = \(\frac{V}{X_{L}}=\frac{220}{7.85}\) = 28 A
Question 14.
A 100 Ω resistor is connected to a 220 V, 50 Hz ac supply.
(a) What is the rms value of current in the circuit?
(b) What is the net power consumed over a full cycle? (NCERT)
Answer :
Given urms = 220 V, f = 50 Hz, lrms = ?, P = ?
(a) lrms = \(\frac{V_{\mathrm{rms}}}{R}=\frac{220}{100}\) = 2.2 A
(b) Power consumed over one cycle of ac P = Vrms × lrms = 220 × 2.2 = 484 W
Question 15.
(a) The peak voltage of an ac supply is 300 V. What is the rms voltage?
(b) The rms value of current in an ac circuit is 10 A. What is the peak current? (NCERT)
Answer:
(a) Vm = 300V, Vrms =?
Using Vrms = \(\frac{V_{\mathrm{m}}}{\sqrt{2}}=\frac{300}{\sqrt{2}}\) = 212.16 V
(b) Using
lm = lrms × V2 = 10 × \(\sqrt{2}\) = 14.14 A
Question 16.
A 44 mH inductor is connected to 220 V, 50 Hz ac supply. Determine the rms value of the current in the circuit. (NCERT)
Answer:
Given L = 44 mH = 44 × 10-3 H, Vrms = 220 V, f = 50Hz,lrms = ?
Using the relation
lrms = \(\frac{V_{\text {rms }}}{x_{L}}=\frac{V_{\text {rms }}}{2 \pi f L}=\frac{220}{2 \times 3.14 \times 50 \times 44 \times 10^{-3}}\)
= 15.9 A
Question 17.
A coil of inductance 0.50 H and resistance 100 Ω is connected to a 240 V, 50 Hz ac supply, (a) What is the maximum current in the coil? (b) What Is the time lag between the voltage maximum and the current maximum? (NCERT)
Answer:
Given L = 0.5 H, R = 100 Ω, Vrms = 240 V,
f= 50 Hz, ω = 2πf= 2 × 3.14 × 50 = 314 s-1 lm = ?
(a) Now
Z = \(\sqrt{R^{2}+X_{L}^{2}}=\sqrt{(100)^{2}+(0.5 \times 314)^{2}}\)
Z = 186.1 Ω
Therefore
l<sub>m</sub> = \(\frac{V_{m}}{Z}=\frac{\sqrt{2} \times V_{\mathrm{rms}}}{Z}=\frac{\sqrt{2} \times 240}{186.1}\)
lm = 1.82 A
(b) Let Φ be the phase angle by which current lags emf, then
tan Φ = \(\frac{X_{L}}{R}=\frac{0.5 \times 314}{100}\) = 1.571
Φ = 57.5° or Φ = 57.5 × π/180 rad
Therefore timw lag
t = \(\frac{\phi T}{2 \pi}=\frac{57.5 \times \pi}{180 \times 2 \pi \times 50}\) = 3.194 × 10-3 s
Question 18.
A coil of 0.01-henry Inductance and 1-ohm resistance is connected to 200 volts, 50 Hz ac supply. Find the Impedance of the circuit and time lag between max alternating voltage and current. (NCERT Exemplar)
Answer:
Given L = 0.01 henry, R = 1 ohm,
Vrms = 200V, f = 50Hz, Z = ?, t = ?
We know that
XL = 2πfL = 2 × 3.14 × 50 × 0.01 = 3.14 ohm
Now
Z = \(\sqrt{R^{2}+X_{\mathrm{L}}^{2}}=\sqrt{(3.14)^{2}+(1)^{2}}\) = 3.3 Ω
Also tan Φ = \(\frac{X_{L}}{R}=\frac{3.14}{1}\)= 3.14
Or
Φ = tan-1 (3.14)
Or
Φ = 72° or 72 × π/180 rad
Now time lag Δt is
Δt = \(\frac{\phi}{\omega}=\frac{72 \times \pi}{180 \times 2 \pi \times 50}=\frac{1}{250}\) s
Question 19.
An electrical device draws 2 kW power from AC mains (voltage 223 V (rms) = V50,000 V). The current differs (lags) in phase by Φ (tan Φ = – 3/4) as compared to voltage.
Find (i)R,
(ii) XC – XL
(iii) lm
Another device has twice the values for R, XC, XL. How are the answers affected? (NCERT Exemplar)
Answer:
Given P = 2 kW = 2000 W, Vrms = 223
= \(\sqrt{50,000}\) V, tan Φ = – 3/4, R = ?,XC – XL = ?, lm = ?
(i)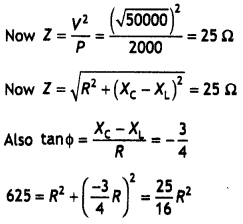
Solving for R we have
R = 20 ohm
(ii) Also XC – XL = (-3/4) R = – 15 Ω
Hence lrms =\(\frac{V}{Z}=\frac{223}{25}\) = 9 A
(iii) lm = \(\sqrt{2}\) × lrms = 1.414 × 9 = 12.6 A
If R, XC, XL, are all doubled, tan Φ does not change. Therefore as Z is doubled, the current becomes halved.
Question 20.
An alternating voltage given by V = 140 sin 314 t is connected across a pure resistor of 50 Ω. Find
(a) the frequency of the source.
(b) the rms current through the resistor. (CBSEAI 2012)
Answer:
R = 50 Ω, f = ?, lrms = ?, Vm = 140 V
Comparing with V = Vm sin 2πft,
we have
2πft = 314 t
or
f = 50 Hz
lrms = \(\frac{V_{r m s}}{R}=\frac{140}{50 \sqrt{2}}\) = 1.98 A
Question 21.
The figure shows a series LCR circuit with L = 5.0 H, C = 80 μF, R = 40 Ω connected to a variable frequency 240 V source. Calculate
(a) The angular frequency of the source drives the circuit at resonance.
(b) The current at the resonating frequency.
(C) The rms potential drops across the capacitor at resonance. (CBSE Delhi 2012)
Answer:
Given L= 5.0 H, C= 80 μF , R = 40 Ω, Vrms = 240 V ωo = ?, lrms = ?, VC = ?
(a)Angutar frequency at resonance
ω0 = \(\sqrt{\frac{1}{L C}}=\sqrt{\frac{1}{5 \times 80 \times 10^{-6}}}\) = 50 s-1
(b)At resonance Z = R = 4O Ω
Now lrms = \(\frac{V_{\mathrm{rms}}}{\mathrm{Z}}=\frac{240}{40}\) = 6 A
(C) VC = lrms × XC = 6 (50 × 80 × 10-6) = 1500 V
Question 22.
The figure shows a series LCR circuit connected to a variable frequency 200 V source with L = 50 mH, C = 80 μF and R = 40 Ω.
Determine
(a) the source frequency which derives the circuit in resonance;
(b) the quality factor (Q) of the circuit. (CBSEAI 2014C)
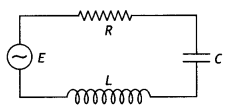
Answer:
(a) Given V = 200 V, L = 50 mH, C = 80 μF, R = 40 Ω
Source frequency at resonance

Question 23.
When an alternating voltage of 220 V is applied across a device X, a current of 0.5 A flows through the circuit and is in phase with the applied voltage. When the same voltage is applied across another device Y, the same current again flows through it, but it leads the voltage by π/2 rattan.
(a) Name the devices X and Y.
(b) Calculate the current flowing In the circuit when the same voltage Is applied across the series combination of the two devices X and Y.
Answer:
(a) The two devices are resistor and capacitor, respectively.
(b) Given l = 0.5 A, V = 220 V, XL = ?, R = ? , l = ?
Now XC and R are equal and are given by
XC = R = \(\frac{220}{0.5}\) = 440 Ω
Hence impedance of the circuit
Z = \(\sqrt{R^{2}+X_{C}^{2}}=\sqrt{2(440)^{2}}\) = 622.25 Ω
Therefore current through the combination is
l = \(\frac{V}{Z}=\frac{220}{622.25}\) = 0.354 A
Question 24.
In the following circuit, calculate (a) the capacitance of the capacitor, if the power factor of the circuit is unity, (b) the Q-factor of this circuit. What is the significance of the Q-factor in a.c. circuit? Given the angular frequency of the a.c. source to be 100 s-1. Calculate the average power dissipated in the circuit. (CBSE Delhi 2017C)
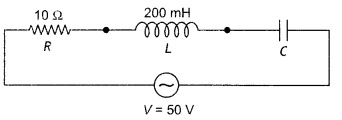
Answer:
(a) when the power factor is unity the circuit is in resonance, therefore, we have
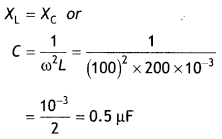
Quality factor determines the sharpness of tuning at resonance. More the Q factor more the sharpness.
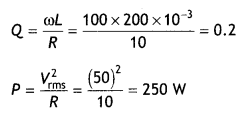
Question 25.
The figure below shows how the reactance of a capacitor varies with frequency.
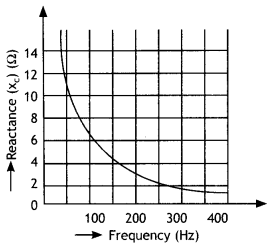
(a) Use the Information on the graph to calculate the value of capacity of the capacitor.
(b) An inductor of inductance L has the same reactance as the capacitor at 100 Hz. Find the value of L.
(c) Using the same axes, draw a graph of reactance against frequency for the inductor.
(d) If this capacitor and inductor were connected in series to a resistor of 10 Ω, what would be the impedance of the combination at 300 Hz?
Answer:
(a) From the graph we find that for a frequency of 100 Hz the capacitive reactance is 6 ohm, therefore
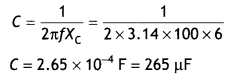
(b) Now given XL = XC at 100 Hz, therefore XL = 6 ohm
(c) The XL – f graph is as shown below.
(d) For a frequency of 300 Hz, XL = 18 ohm and XC = 2 ohm. If resistance is 10 ohm then the impedance of the combination is
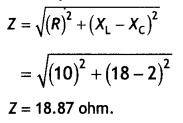
Question 26.
The given graphs (i) and (ii) represent the variation of the opposition offered by the circuit element to the flow of alternating current, with the frequency of the applied emf. Identify the circuit element corresponding to each graph.
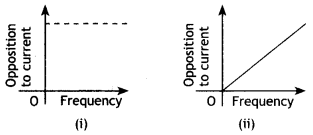
A circuit is set up by connecting L= 100 mH, C = 5 μf and R =100 Ω in series. An alternating emf of (150 \(\sqrt{2}\)) volt, (500/π) Hz is applied across this series combination. Calculate the impedance of the circuit. What is the average power dissipated in (a) the resistor, (b) the capacitor, (c) the inductor, and (d) the complete circuit?
Answer:
(a) Resistor and (b) Inductor
Given L = 100 mH = 0.1 H, C = 5μF = 5 × 10-6F, R=100 Ω,

Average power dissipated in
(a) the resistor P = l2R = (1.5)2 × 100 = 225 W
(b) power in inductor is zero.
(c) power in capacitor is zero.
(d) the complete circuit is same as that in a resistor.
Question 27.
The output voltage of an ideal transformer, connected to a 240 V ac mains, is 24 V. When this transformer is used to light a bulb with rating 24 V, 24 W, calculate the current in the primary coil of the circuit.
Answer:
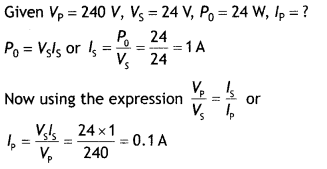
Question 28.
An ac generator consists of a coil of 50 turns and an area of 2.5 m2 rotating at an angular speed of 60 rads-1 in a uniform magnetic field B = 0.2 tesla, between the two fixed pole pieces. The resistance of the circuit including that of the coil is 500 ohm (a) Calculate the maximum current drawn from the generator. (b) What is the flux when the current is zero and (c) Would the generator work if the coil were stationary and instead the pole pieces rotated together with the same speed as above? Give a reason for your answer.
Answer:
Given n = 50, A = 2.5 m2, ω = 60 rads-1, B = 0.2 T, R = 500 ohm, l0 = ?
(a) The maximum induced emf produced in the coil is
ε0 = nBAω = 50 × 0.2 × 2.5 × 60 = 1500 V
Therefore maximum current in the circuit is
l0 = \(\frac{\varepsilon_{0}}{R}=\frac{1500}{500}\) = 3 A
(b) The flux in this case is maximum and is given by Φ = nBA = 50 × 0.2 × 2.5 = 25 Wb
(c) Yes, for a generator to work there should be relative motion between the magnet and the coil.
Question 29.
The primary coil of an ideal step-up transformer has 100 turns and the transformation ratio is also 100. The input voltage and the powers are 220 V and 1100 W respectively. Calculate:
(a) number of turns in the secondary
(b) the current In the primary
(C) the voltage across the secondary
(d) the current in the secondary
(e) power in the secondary
Answer:
Here, N = 100, Transformation ratio = 100
Vp = 220 V, Pp = 1100W
(a) Number of turns in the secondary
Ns = Np × Transformation ratio
= 100 × 100 = 10,000
(b) Current in the primary
lp = \(\frac{P_{p}}{V_{p}}=\frac{1100}{220}\) = 5 A
(C) Voltage across the secondary Vs = Vp × transformation ratio
= 220 × 1oo = 22000 V
(d) Current in the secondary
ls = \(\frac{V_{p} l_{p}}{V_{s}}=\frac{220 \times 5}{22000}\) = 0.05 A
(e) Power in the secondary = power in the primary (ideal transformer) = 1100 W
Question 30.
Calculate the current drawn by the primary of a transformer which steps down 200 V to 20 V to operate a device of resistance 20 Q. Assume the efficiency of the transformer to be 80 %.
Answer:
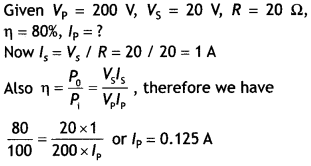
Question 31.
The primary of a transformer has 200 turns and the secondary has 1000 turns. If the power output from the transformer at 1000 V is 9 kW, calculate
(a) The primary voltage and
(b) The heat loss in the primary coil if the resistance of the primary is 0.2 Ω and the efficiency of the transformer is 90%.
Answer:

Question 32.
A power transmission line feeds input power at 2300 V to a step-down transformer with its primary windings having 4000 turns. What should be the number of turns in the secondary In order to get output power at 230 V? (NCERT)
Answer:
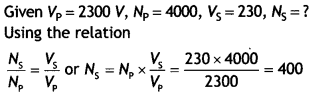
Question 33.
A small town with a demand of 800 kW of electric power at 220 V situated 15 km away from an electric plant generating power at 440 V The resistance of the two wirelines carrying power is 0.5 Ω per km. The town gets power from the line through a 4000 – 220 V step-down transformer at a sub-station in the town.
(a) Estimate the line power loss in the form of heat.
(b) How much power must the plant supply, assuming their negligible power loss due to leakage?
(c) Characterise the step-up transformer at the plant. (NCERT)
Answer:
Electric power required P = 800 kW = 800 × 103 W
Voltage required V0 = 220 V
Distance of the power station
d = 15km = 15 × 103m
Resistance per kilometre = 0.5 ohm per km
Total resistance R = 0.5 × 2 × 15 = 15 ohm
Input voltage Vi = 440 V
Primary voltage of transformer εp = 4000 V
Secondary voltage of transformer εs = 220 V
(a) Rms value of current in the two wire line
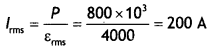
Therefore power loss along the line
= l2rmsR = (200)2 × 15 = 600 kW
(b) Assuming negligible loss due to leakage Total power supply = power demand of town + power loss along the line
P = 800 kW + 600 kW = 1400 kW
(c) Voltage drop on the line = 200 × 15 = 3000 V
Hence voltage at the generation station
V= 4000 + 3000 = 7000 V
Therefore the step-up transformer at the plant is 440 V – 7000 V.
Question 34.
A 60 W load is connected to the secondary of a transformer whose primary draws line voltage. If a current of 0.54 A flows in the load, what is the current in the primary coil? Comment on the type of transformer being used. (NCERT Exemplar)
Answer:
Given Ps = 60 W, ls = 0.54 A
We know that P=V I, therefore we have Vs = Ps/ls = 60 /0.54 = 110 V
Therefore the transformer is a step-down transformer, whose transformation ratio is 1/2
Therefore
lp = 1/2 × ls = 1/2 × 0.54 = 0.27 A