On this page, you will find Comparing Quantities Class 7 Notes Maths Chapter 8 Pdf free download. CBSE NCERT Class 7 Maths Notes Chapter 8 Comparing Quantities will seemingly help them to revise the important concepts in less time.
CBSE Class 7 Maths Chapter 8 Notes Comparing Quantities
Comparing Quantities Class 7 Notes Conceptual Facts
1. Ratio: Comparison of two quantities of same kind and with same unit is called ratio.
For example: a : b or \(\frac{a}{b}\) where a is called Antecedent and b Consequent. b
2. Ratio in simplest form: A ratio is said to be in simplest form if its antecedent and consequent have no common factor other than.
For example: \(\frac{2}{3}, \frac{3}{7}, \frac{2}{5}, \frac{6}{7}\) etc. or 2 : 3, 3 : 7, 2 : 5 and 6 : 7 etc.
3. Equivalent ratios: Two ratios can be compared by converting then into like fractions. If the two factions are equal, then they are called as equivalent ratio.
For example: 15 : 20 is equivalent to 3 : 4.
Check whether 1: 2 and 2 : 5 are equivalent.
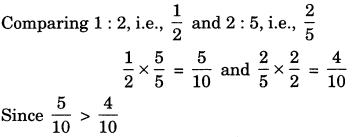
∴ 1 : 2 and 2 : 5 are not equivalent ratios.
4. Comparison of ratios: Let us take from two ratios 2 : 3 and 4 : 5
2 : 3 = \(\frac{2}{3}\) and 4 : 5 \(\frac{2}{3}\)
= 2 x 5 and 3 x 4
2 x 5 and 3 x 4 (By Cross-multiplicative)
10 and 12
\(10<12 \Rightarrow \frac{2}{3}<\frac{4}{5}\)
Hence 2:3< 4:5
We can also compare more than two ratios.
5. Percentage: Ratios can also be compared by converting it into percent i.e. per hundred.
For example:
Let us take two ratios \(\frac{4}{5} \text { and } \frac{3}{4}\) converting into Percentage, we have
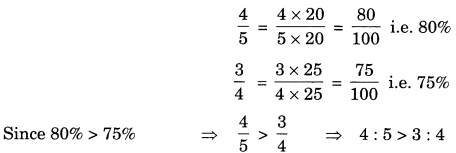
6. Proportion: When two ratios are equivalent, then the four quantities are in proportion.
Let a : b and c : d are equivalent ratios
a : b :: c : d [:: Symbol of proportion]
\(\frac{a}{b}=\frac{c}{d}\) ⇒ a x d = c x b
a and d are called extremes and b and c are called means
∴ Product of extremes = Product of means
7. Continued proportion: If a, b and c be three quantities such that a: b:: b: c, then a, b, c are in continued proportion.
\(\frac{a}{b}=\frac{b}{c} \quad \Rightarrow \quad b^{2}=a c \Rightarrow b=\sqrt{a c}\)
8. Unitary method: In this method, we find the value of unit quantity and then the value of required quantity is calculated. There are two types of variation.
- Direction variation
- Inverse variation
9. Conversion of a fraction into percent: To convert \(\frac{2}{5}\) into percent, we have
\(\frac{2}{5}\) x 100% =40%
10. Conversion of percent into fraction: To convert 20% into fraction, we have
20% = \(\frac{20}{100}=\frac{1}{5}\)
11. Conversion of a ratio into per cent: To convert 4 : 5 into per cent, we have
4:5= \(\frac{4}{5}\) x 100% = 80%
12. Conversion of a percent into ratio: To convert 75% into ratio, we have
75% = \(\frac{75}{100}=\frac{3}{4}\) i.e, 3:4
13. Simple interest:
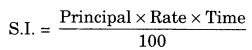
[Here SP means selling price and CP means cost price]
Profit and Loss per cent are always calculated on CP.