
On this page, you will find Comparing Quantities Class 8 Notes Maths Chapter 8 Pdf free download. CBSE NCERT Class 8 Maths Notes Chapter 8 Comparing Quantities will seemingly help them to revise the important concepts in less time.
CBSE Class 8 Maths Chapter 8 Notes Comparing Quantities
Comparing Quantities Class 8 Notes Conceptual Facts
1. In every hundred or per hundred is called as percent. For example: 30% means 30 in every hundred.
To change a percentage to a fraction:
40% \(\frac{40}{100}\)=0.4 , 125% = \(\frac{125}{100}\)=1.25
2. Percentage increase and decrease
Increase 240 by 10% = 240 + \(\frac{10}{100}\) x 240 = 240 + 24 = 264
Decrease 180 by 18% = 180 – \(\frac{18}{100}\) x 180 = 180 – 32.4 = 147.6
3. Profit and Loss
Profit = SP – CP,Loss= CP – SP
![]()
4. Profit and Loss are always calculated on CP.
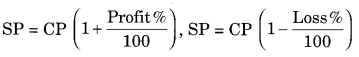
5. Marked Price: The printed or the tagged price of an article is known as marked price or MP.
6. Discount: The deduction allowed on the market price is called Discount. It is generally given in percent.
7. Net Price: The selling price after the discount to an article is called its Net Price.
SP = MP – Discount
\(\mathrm{MP}=\left(\frac{100 \times \mathrm{SP}}{100-\mathrm{Discount} \%}\right)\)
8. Sales Tax: Sales tax is a tax levied by the Government on the selling price of an article at a rate given by the Government.
9. Value Added Tax (VAT): VAT is an extra tax which is levied and collected by State Government in lieu of State Tax.
10. Simple Interest:
\(\mathrm{SI}=\frac{\text { Principal } \times \text { Rate } \times \text { Time }}{100}\)
11. Compound Interest: Cl = Amount – Principal
\(\mathrm{CI}=\mathrm{P}\left(1+\frac{r}{100}\right)^{n}-\mathrm{P}\)
Amount = \(\mathrm{P}\left(1+\frac{r}{100}\right)^{n}\) where n represent time in years.
12. Conversion of Period:
- If interest is calculated half-yearly or semi-annually, then ‘r’ is halved and T is doubled.
- If interest is calculated quarterly, then V’ is one-fourth and T is four times.