By going through these CBSE Class 11 Maths Notes Chapter 5 Complex Numbers and Quadratic Equations Class 11 Notes, students can recall all the concepts quickly.
Complex Numbers and Quadratic Equations Notes Class 11 Maths Chapter 5
Imaginary Numbers: A number whose square is negative, is known as an imaginary number, e.g. : \(\sqrt{-1}, \sqrt{-2}\), etc.
\(\sqrt{-1}\) is denoted by the Greek letter i (iota).
Powers of i : i1 = – 1; i2= – 1; i3 = — i, i4 = 1, etc.
An Important Result : For any two real numbers a and b,
\(\sqrt{a} \times \sqrt{b}=\sqrt{a b}\) is true only when at least one of a and b is either 0 or positive.
In fact, \(\sqrt{-a} \times \sqrt{-b}=(i \sqrt{a})(i \sqrt{b})=i^{2} \sqrt{a b}=-\sqrt{a b}\), where a and b are positive real numbers.
Complex Number : Any number of the form x + iy, where x, y are real numbers and i \(\sqrt{-1}\) is called a complex number.
It is denoted by z, i.e., z = x + iy. The real and imaginary parts of a complex number z are denoted by Re(z) and Im(z) respectively. Thus, if z = x + iy, then Re(z) = x and Im(z) = y.
Note : Every real number is a complex number, for if a e R, it can be written as a – a + i0.
Purely Real and Purely Imaginary Numbers : A complex number z is said to be
(i) purely real, if Im(z) = 0.
(ii) purely imaginary, if Re(z) = 0.
Conjugate of a Complex Number : The conjugate of a complex number z, denoted by \(\bar{z}\) is the complex number obtained by changing the sign of imaginary part of z i.e., if z = a + ib, then \(\bar{z}\) = a-ib.
Modulus of a Complex Number: The modulus of a complex number, z- a + ib, denoted by |z |, is defined as |z | = \(\sqrt{x^{2}+y^{2}}\)
Sum, Difference and Product of Complex Numbers : For any complex numbers z1 = a + ib and z2 = c + id, it is defined as
(i) Z1 + z2 = (a + ib) + (c + id) = (a + c) + i(b + d).
(ii) z1 – z2 = (a + ib) – (c + id) = (a -c) + i(b – d).
(iii) z1z2 = (a + ib)(c + id) = (ac -bd) + i(ad – bc).
Properties of Complex Numbers:
1. A real number can never be equal to an imaginary number.
2. (a + ib) = 0 ⇔ a = 0 and 6 = 0.
3. Two complex numbers are equal only when their real and imaginary parts are separately equal.
i.e., if a + ib = c + id, then a = c and b = d.
4. If z is a complex number, then :
(i) (\(\bar{z}\)) = z
(ii) (z + \(\bar{z}\)) is real.
(iii) (z – \(\bar{z}\)) is zero or an imaginary number.
(iv) z + \(\bar{z}\) = 2Re(z) and (z – \(\bar{z}\)) = 2iIm(z).
(v) z\(\bar{z}\) – |z |2 and, therefore, z\(\bar{z}\) is real.
5. If z1 and z2 are complex numbers, then :
(i) \(\left(\overline{z_{1}+z_{2}}\right)=\overline{z_{1}}+\overline{z_{2}}\)
(ii) \(\left(\overline{z_{1}-z_{2}}\right)=\overline{z_{1}}-\overline{z_{2}}\)
(iii) \(\left(\overline{z_{1} z_{2}}\right)=\overline{z_{1}} \cdot \overline{z_{2}}\)
(iv) \(\left|z_{1} z_{2}\right|=\left|z_{1}\right|\left|z_{2}\right|\)
6. For any complex number z, |z | = 0 ⇔ z = 0.
7. The sum and product of two complex numbers are real if and only if they are conjugate of each other.
8. The conjugate and the reciprocal of a non-zero complex number z are equal if and only if | z | = 1.
9. Reciprocal or multiplicative inverse of a + ib
= \(\frac{1}{a+i b}=\frac{1}{a+i b} \times \frac{a-i b}{a-i b}=\frac{a}{a^{2}+b^{2}}-i\left(\frac{b}{a^{2}+b^{2}}\right)\)
10. For any integer k,
(i) i2k = (-1)k , i2k+ 1 = (- 1)ki
(ii) i4k = (i4)k = 1, i4k+ 1 = i4k+2 = i2 = -1,
i4k+3 = i3 = i2 x i = -i
Geometrical Representation of a Complex Number : To every complex number z = x + iy, there is one and only one point P(x, y) in the plane, and conversely to every point (x,y) in the plane, there is one and only one complex number z = x + iy.
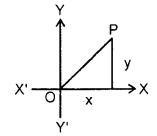
The plane, representing the complex numbers, as an ordered pair of real numbers is called the Complex plane or Gaussian plane or Argand plane.
Modulus and Amplitude of a Complex Number : Let a poin^ P represents a complex number z = x + iy in the complex plane. Then, the length OP is called the modulus of the complex number z and is denoted by |z|.
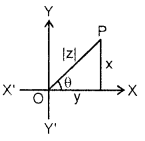
∴ |z| = OP = |x + iy|
= \(\sqrt{x^{2}+y^{2}}\) .
The angle XOP = θ is called the amplitude or argument of 2 and is written as amp. z or arg. z. The value of θ satisfying – π < θ < π is called the principal value of amp z.
Polar Form of a Complex Number : Let z – a + ib be represented by P(a, b).
Let OP = r, ∠XOP = θ.
Then, a – rcos θ,
b = rsinθ
= r2 = a2 + b2
⇒ r = |2|
and tanθ = \(\frac{b}{a}\)
⇒ cosθ = \(\frac{a}{r}\) ,sinθ = \(\frac{b}{r}\).
The form 2 = r(cos θ + isin θ) is called the Polar Form.
Polynomial Equation : A polynomial equation of a degree x has n roots.
Solutions of Quadratic Equation: The solutions of quadratic equation
ax2 + bx + c = 0,
where a, b, c ∈ R, a ≠ 0, b22 – 4ac < 0 are given by
x = \(\frac{-b \pm\left(\sqrt{4 a c-b^{2}}\right) i}{2 i}\)
D = b2 – 4ac is called the discriminant of the quadratic equation.