On this page, you will find Congruence of Triangles Class 7 Notes Maths Chapter 7 Pdf free download. CBSE NCERT Class 7 Maths Notes Chapter 7 Congruence of Triangles will seemingly help them to revise the important concepts in less time.
CBSE Class 7 Maths Chapter 7 Notes Congruence of Triangles
Congruence of Triangles Class 7 Notes Conceptual Facts
1. Congruence: The objects having same shape and same size are called congruent. The symbol of congruence is ‘≅’.
Example:
- Two coins of same denominations.
- Two toys made of the same mould.
- Two biscuits in the same packet.
2. Congruence of triangles: Two triangles are said to be congruent if all the six elements of one triangle are equal to the corresponding six elements of the other.
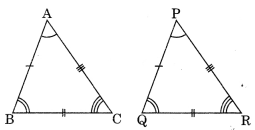
Example: ΔABC is congruent to ΔPQR
if AB = PQ, BC = QR, AC = PR
and ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R
∴ ΔABC ≅ ΔPQR
3. Congruence of plane figures: Two plane figures are said to be congruent if each superposed on the other i.e., covers each other properly.
Examples:
- Leaves of the same branch.
- Two squares with same length of sides.
- Two circles with same radii.
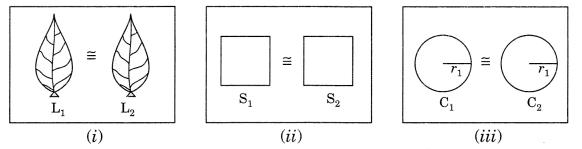
4. Congruence of line segments:
Two line segments are said to be congruent if they have equal lengths.
Example:
∵ \(\overline{\mathrm{PQ}}=\overline{\mathrm{RS}}\) = 6.5 cm
∴ \(\overline{\mathrm{PQ}} \cong \overline{\mathrm{RS}}\)
5. Congruence of angles:
Two angles are said to be congruent if they have the same degree measure.
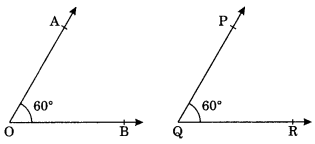
Example:
∠AOB = 60° and ∠PQR = 60°
∴ ∠AOB ≅ ∠PQR [means superpose]
ar m ∠AOB = m∠PQR
Conditions for congruence of triangles:
1. Side-Side-Side (SSS): If three sides of one triangle are respectively equal the corresponding sides of the other triangle, then the two triangles are congruent by SSS criterion.
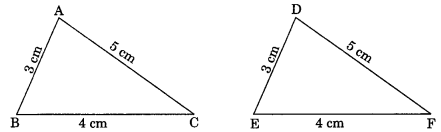
In ΔABC and ΔDEF, we have
AB = DE = 3 cm
BC = EF = 4 cm and
AC = DF = 5 cm
∴ ΔABC ≅ ΔDEF (By SSS criterion)
2. Side-Angle-Side (SAS): If two sides and the included angle of one triangle are respectively equal to the corresponding two sides and their included angle, then the two triangles are congruent (by SAS criterion).
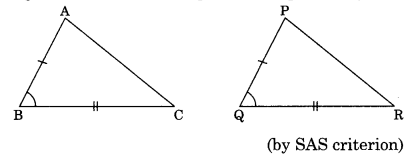
In ΔABC and ΔPQR,
we have AB = PQ BC = QR
and ∠B = ∠Q
∴ ΔABC ≅ ΔPQR
3. Angle-Side-Angle (ASA): If two angles and the included side of one triangle are respectively equal to the corresponding two angles and the included side, then the triangles are congruent (by ASA criterion).
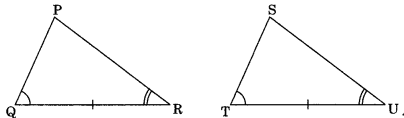
In ΔPQR and ΔSTU, we have
∠Q = ∠T and ∠R = ∠U
QR = TU
∴ ΔPQR ≅ ΔSTU (by ASA criterion)
4. Right-Angle-Hypotenuse-Side (RHS): If the right angle, hypotenuse and one side of one triangle
are respectively equal to the corresponding right angle, hypotenuse and side of the other triangle, then the two triangles are congruent m (by RHS).
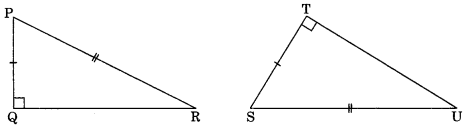
In ΔPQR and ΔSTU,
we have PQ = ST
hypt. PR = hypt. SU
∠Q = ∠T = 90°
∴ ΔPQR ≅ ΔSTU