By going through these CBSE Class 11 Maths Notes Chapter 11 Conic Sections Class 11 Notes, students can recall all the concepts quickly.
Conic Sections Notes Class 11 Maths Chapter 11
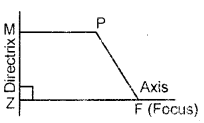
Conic : Let T be a fixed line and F be a fixed point (not on line T).
Let P be any point in the plane of the line T and the point F. Then, the set of all points P, such that | FP | = e | PM |, where M is the foot’ of perpendicular from P on the line l and e > 0 is . a fixed real number is called a conic.
Notes :
- The fixed point F is called focus of the conic and the fixed line T is called directrix of the conic associated with F.
- The positive real number e is called eccentricity of the conic.
- A line through the focus F and perpendicular to the directrix l is called axis of the conic.
- The point of intersection of the conic and its axis is called
vertex. - A conic with eccentricity ‘e’ is called
(i) a parabola, if e = 1. (ii) an ellipse, if e < 1. (iii) a hyperbola if e > 1..
Parabola : Let T be a fixed line and F be a fixed point (not on 1). Let P be any point in the plane of line l and the point F. Let M be the foot of perpendicular from P on the line l. Then, the set of all points P such that | FP | = | PM | is called a parabola.
Equation of the Parabola (Standard Form): The equation of the parabola in the standard form is y2 = 4ax.
Latus Rectum : The latus rectum of conic is the chord passing through the focus and perpendicular to its axis.
Length of Latus Rectum : The length of the latus rectum of the parabola y2 = 4ax is 4a.
Focal Distance : The distance of any point on parabola from the focus is called focal distance of that point.
Focal Chord : Any chord that passes through the focus of the parabola is called a focal chord of the parabola.
The focal distance of a point P(x1, y1 of the parabola y2 = 4ax is a + x1
Main Facts about Four Standard Forms of Parabola
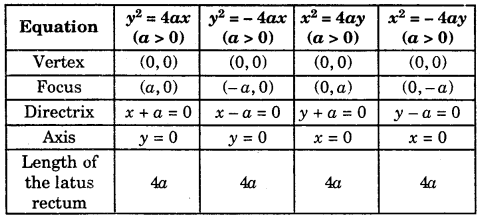
Ellipse : Let l be a fixed line, F be a fixed point (not on l). Let P be any point in the plane of the line l and the point F.
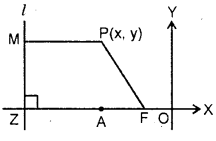
Let M be the foot of perpendicular from P on the line l.
Then, the set of all points P such that | FP | = e | PM | (0 < e < 1) is called an ellipse.
Notes : 1. The fixed line is called directrix of the ellipse.
2. The fixed point F is called focus of the ellipse.
3. The positive real number e < 1 is called eccentricity of the ellipse.
Standard form of an Ellipse : The equation of the ellipse in the standard form is \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, where b2 = a2( 1 – e2) = a2 – a2e2.
Putting ae = c. Therefore, c2 = a2 – b2.
Note: The ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 has two foci, namely (ae,o) and (- ae, 0) and their respective directrices are x – \(\frac{a}{e}\) = 0 and x + \(\frac{a}{e}\) = 0.
Main Facts about two Standard forms of Ellipse
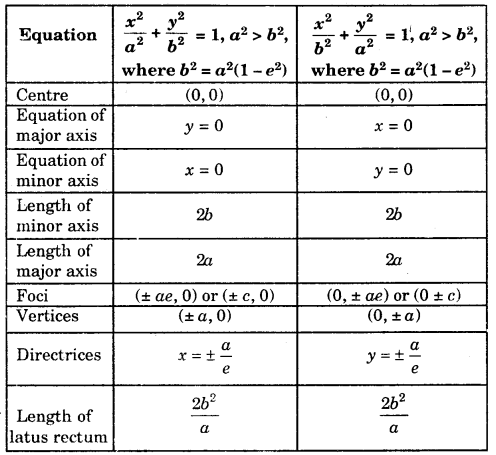
Notes : 1. The focal distances of any point (x1, y1) of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 are a ± ex1
2. Sum of the focal distances of a point of the ellipse is equal to length of the major axis.
Hyperbola: Let l be a fixed line and F be a fixed point (not on l). Let P be any point in the plane of the line l and the point F. Let M be the foot of perpendicular from P on the line l. Then, the set of all points P such that | FP | = e | PM | (e > 1) is called a hyperbola.
2. Sum of the focal distances of a length of the major axis.
Hyperbola: Let l be a fixed line and F be a fixed point (not on l). Let P be any point in the plane of the line l and the point F. Let M be the foot of perpendicular from P on the line l. Then, the set of all points P such that | FP | = e | PM | (e > 1) is called a hyperbola.
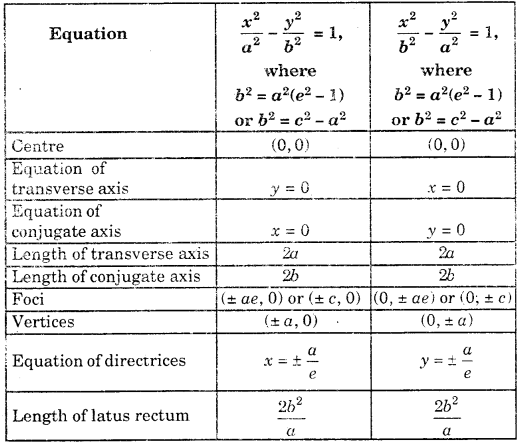
Standard form of Hyperbola : The equation of a hyperbola in the standard form is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, where b2 = a2(e2 – 1). Putting ae -c, b2 – c2 – a2 or c2 – a2 + b2.
Notes: 1. The hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 has two foci namely (- ae, 0) and (ae, 0) with two respective directrices as x + \(\frac{a}{e}\) = 0 and x – \(-\frac{a}{e}\) = 0
2. | ex1 – a | and | ex1 + a | are the focal distances of any point (x1, y1) on the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
Main facts about two standard forms of hyperbola
Circle : The locus of a point which moves in a plane such that its distance from a fixed point, in the plane, is always a constant, is called a circle. The fixed point is called the centre and the constant distance is called the Radius of the circle.
Equation of the Circle : The equation of a circle with centre (h, k) and radius V’ is given by (x – h)2 + (y – k)2 = r2.
If the centre of a circle is origin and radius is ‘r’ then its equation is x2 + y2 = r2.
General Equation of a Circle : The general equation of a circle is x2 + y2 + 2gx + 2fy + c = 0.
Its centre is (-g,-f) and radius = \(\sqrt{g^{2}+f^{2}-c}\)
Note : 1. If g2 + f2 – c = 0, then radius = 0.
In this case, x2 +y2 + 2gx + 2fy + c = 0 represents a circle whose radius is zero. Such a circle is called a Point Circle, [i.e., it represents the point (-g, -f)].
2. If g2 + f2 – c < 0, then radius is non-real. In this case, x2 +y2 + 2gx + 2fy + c = 0 represents the empty set. 3. If g2 + f2 – c > 0, then radius is real and therefore,
x2 + y2 + 2gx + 2fy + c = 0 represents a circle whose centre is at the point (- g,- f) and radius = \(\sqrt{g^{2}+f^{2}-c}\). (where g2 + f2 – c > 0).
Conditions for an Equation to Represent a Circle :
(i) It should be a second degree equation in x and y.
(ii) Coefficient of x2 = Coefficient of y2 ≠ 0.
(iii) It should not contain any term of the product xy.
Method to find the centre, radius of a circle :
(i) Write the equation of the circle with the coefficient of x2 and y2 being unity.
(ii) Compare this with x2 + y2 + 2gx + 2fy + c = 0 and find the value of g,f and c.
(iii) Then, (-g,-f) is the centre and \(\sqrt{g^{2}+f^{2}-c}\) is the radius of the circle.