Here we are providing Coordinate Geometry Class 10 Extra Questions Maths Chapter 7 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/
Extra Questions for Class 10 Maths Coordinate Geometry with Answers Solutions
Extra Questions for Class 10 Maths Chapter 7 Coordinate Geometry with Solutions Answers
Coordinate Geometry Class 10 Extra Questions Very Short Answer Type
Answer the following questions in one word, one sentence or as per the exact requirement of the question.
Coordinate Geometry Class 10 Extra Questions Question 1.
What is the area of the triangle formed by the points 0 (0, 0), A (-3, 0) and B (5, 0)?
Solution:
Area of ∆OAB = \(\frac{1}{2}\) [0(0 – 1) – 3(0 – 0) + 5(0 – 0)] = 0
⇒ Given points are collinear
Coordinate Geometry Extra Questions Class 10 Question 2.
If the centroid of triangle formed by points P (a, b), Q (b, c) and R (c, a) is at the origin, what is the value of a + b + c?
Solution:
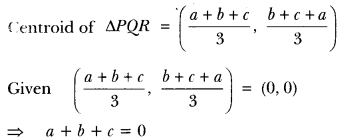
Coordinate Geometry Class 10 Extra Questions With Solutions Pdf Question 3.
AOBC is a rectangle whose three vertices are A (0, 3), 0 (0, 0) and B (5, 0). Find the length of its diagonal.
Solution:
![]()
Class 10 Coordinate Geometry Extra Questions Question 4.
Find the value of a, so that the point (3, a) lie on the line 2x – 3y = 5.
Solution:
Since (3, a) lies on the line 2x – 3y = 5
Then 2(3) – 3(a) = 5
– 3a = 5 – 6
– 3a = -1
⇒ a = \(\frac{1}{3}\)
Coordinate Geometry Class 10 Important Questions Question 5.
Find distance between the points (0, 5) and (-5, 0).
Solution:
Here x1 = 0, y1 = 5, x2 = -5 and y2 = 0)
![]()
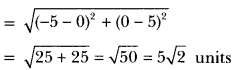
Extra Questions Of Coordinate Geometry Class 10 Question 6.
Find the distance of the point (-6,8) from the origin.
Solution:
Here x1 = -6, y1 = 8
x2 = 0, y2 = 0
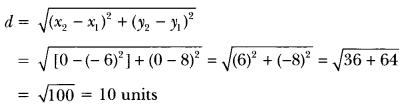
Class 10 Maths Chapter 7 Extra Questions With Solutions Question 7.
If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?
Solution:
Using distance formula
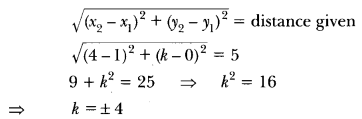
Coordinate Geometry Class 10 Extra Questions With Solutions Question 8.
If the points A (1, 2), B (0, 0) and C (a, b) are collinear, then what is the relation between a and b?
Solution:
Points A, B and C are collinear
⇒ 1(0 – b) + 0 (b – 2) + a(2 – 0) = 0
⇒ -b + 2a = 0 or 2a = b
Extra Questions On Coordinate Geometry Class 10 Question 9.
Find the ratio in which the line segment joining the points (-3, 10) and (6, – 8) is divided by (-1, 6).
Solution:
In Fig. 6.6, let the point P(-1, 6) divides the line joining A(-3, 10) and B (6, -8) in the ratio k : 1

Hence, the point P divides AB in the ratio 2 : 7.
Coordinate Geometry Class 10 Extra Questions Pdf Question 10.
The coordinates of the points P and Q are respectively (4, -3) and (-1, 7). Find the abscissa of a point R on the line segment PQ such that \(\frac{P R}{P Q}\) = \(\frac{3}{5}\).
Solution:
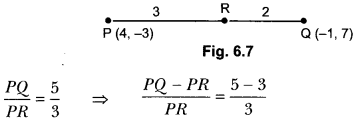
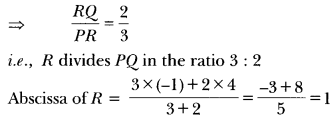
Coordinate Geometry Class 10 Extra Questions Short Answer Type 1
Coordinate Geometry Class 10 Questions With Solutions Question 1.
Write the coordinates of a point on x-axis which is equidistant from the points (-3, 4) and (2, 5).
Solution:
Let the required point be (x, 0).
Since, (x, 0) is equidistant from the points (-3, 4) and (2, 5) .
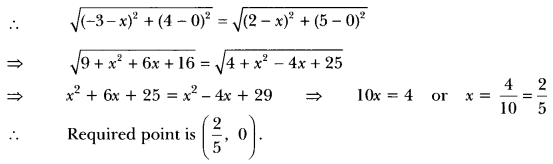
Class 10 Maths Coordinate Geometry Extra Questions Question 2.
Find the values of x for which the distance between the points P (2, -3) and Q (x, 5) is 10.
Solution:
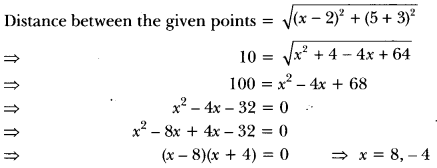
Coordinate Geometry Questions Class 10 Question 3.
What is the distance between the points (10 cos 30°, 0) and (0, 10 cos 60°)?
Solution:
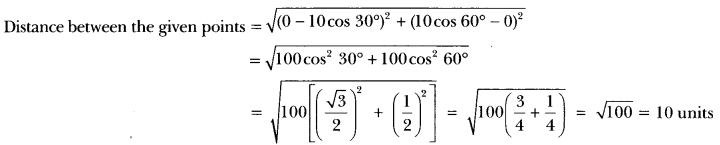
Extra Questions On Distance Formula Class 10 Question 4.
In Fig. 6.8, if A(-1, 3), B(1, -1) and C (5, 1) are the vertices of a triangle ABC, what is the length of the median through vertex A?
Solution:”
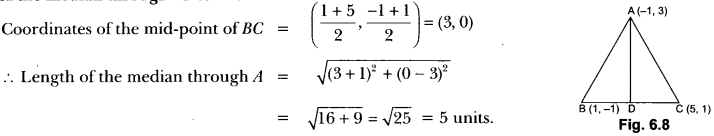
Ch 7 Maths Class 10 Extra Questions Question 5.
Find the ratio in which the line segment joining the points P (3, -6) and Q (5,3) is divided by the x-axis.
Solution:
Let the required ratio be λ : 1

Given that this point lies on the x-axis
![]()
Thus, the required ratio is 2 : 1.
Class 10 Maths Ch 7 Extra Questions Question 6.
Point P (5, -3) is one of the two points of trisection of the line segment joining the points A (7, -2) and B (1, -5). State true or false and justify your answer.
Solution:
Points of trisection of line segment AB are given by
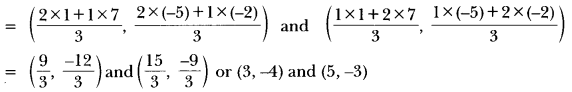
∴ Given statement is true.
Coordinate Geometry Extra Questions Question 7.
Show that ∆ABC, where A(-2, 0), B(2, 0), C(0, 2) and APQR where P(-4, 0), Q(4, 0), R(0,4) are similar triangles.
OR
Show that ∆ABC with vertices A(-2, 0), B(0, 2) and C(2, 0) is similar to ∆DEF with vertices D(-4, 0), F(4,0) and E(0, 4).
[∆PQR is replaced by ∆DEF]
Solution:
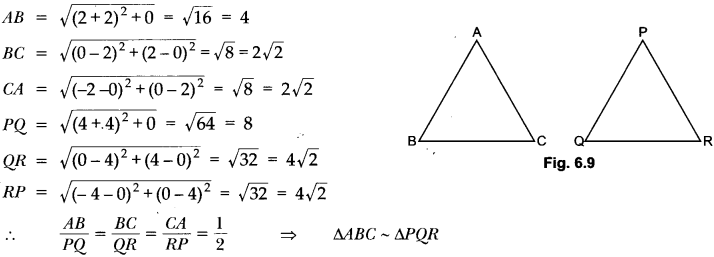
Chapter 7 Maths Class 10 Extra Questions Question 8.
Point P (0, 2) is the point of intersection of y-axis and perpendicular bisector of line segment joining the points, A (-1, 1) and B (3, 3). State true or false and justify your answer.
Solution:
The point P (0, 2) lies on y-axis
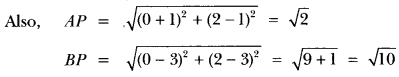
AP ≠ BP
∴ P(0, 2) does not lie on the perpendicular bisector of AB. So, given statement is false.
Coordinate Geometry Class 10 Questions Question 9.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Solution:
Let A (5,-2), B (6, 4) and C (7, -2) be the vertices of a triangle
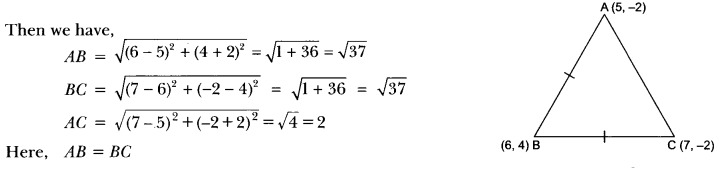
Here, AB = BC
∴ ∆ABC is an isosceles triangle.
Class 10 Coordinate Geometry Important Questions Question 10.
If (1, 2), (4, y), (x, 6) and (3,5) are the vertices of a parallelogram taken in order, find x and y.
Solution:
Let A(1, 2), B(4, y), C(x, 6) and D(3, 5) be the vertices of a parallelogram ABCD.
Since, the diagonals of a parallelogram bisect each other.
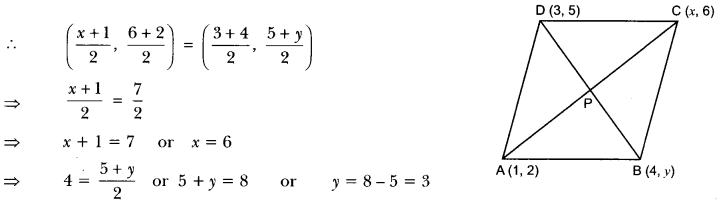
Hence, x = 6 and y = 3.
Question 11.
Find the ratio in which y-axis divides the line segment joining the points A(5, -6) and B(-1, 4). Also, find the coordinates of the point of division.
Solution:
Let the point on y-axis be P(0, y) and AP : PB = k : 1
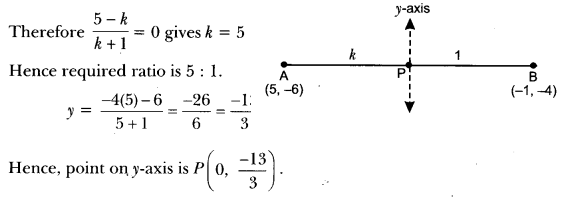
Question 12.
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
Solution:
∵ P divides AB in the ratio 1 : 2.
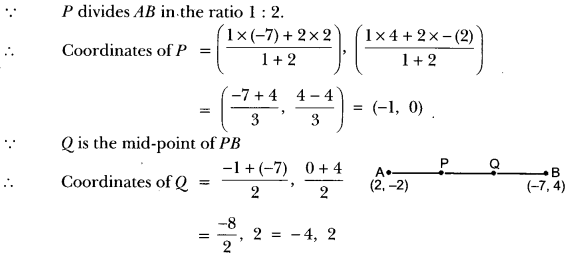
Question 13.
Find the ratio in which the point (-3, k) divides the line-segment joining the points (-5, 4) and (-2, 3). Also find the value of k.
Solution:
Let Q divide AB in the ratio of p : 1
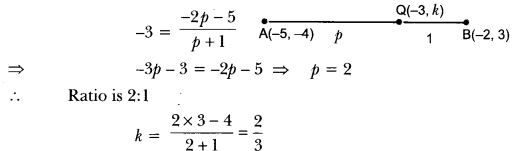
Question 14.
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, -5) and R(-3, 6), find the coordinates of P.
Solution:
Let the point P be (2y, y)
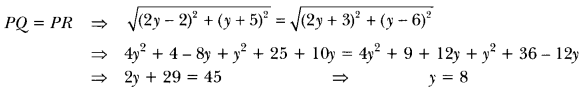
Hence, coordinates of point P are (16, 8).
Question 15.
If two adjacent vertices of a parallelogram are (3, 2) and (-1, 0) and the diagonals intersect at (2, -5), then find the coordinates of the other two vertices.
Solution:
Let other two coordinates are (x, y) and (x’, y’)
O is mid point of AC and BD
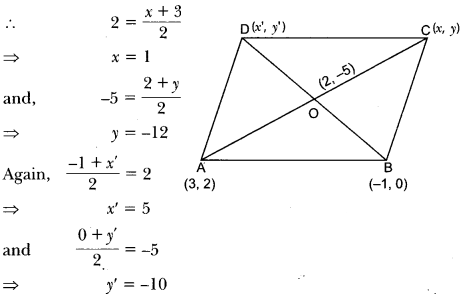
Hence, co-ordinates are (1, -12) and (5, -10).
Coordinate Geometry Class 10 Extra Questions Short Answer Type 2
Question 1.
Determine, if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Solution:
Let A (1, 5), B (2, 3) and C (-2, -11) be the given points. Then we have
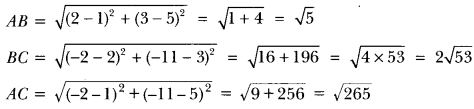
Clearly, AB + BC ≠ AC
∴ A, B, C are not collinear.
Question 2.
Find the distance between the following pairs of points:
(i) (-5, 7), (-1, 3)
(ii) (a, b), (-a, -b)
Solution:
(i) Let two given points be A (-5, 7) and B (-1, 3).
Thus, we have x1 = -5 and x2 = -1
y1 = 7 and y2 = 3
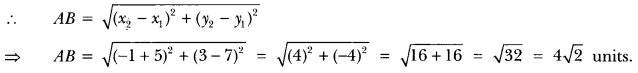
(ii) Let two given points be A (a,b) and B(-a, -b)
Here, x1 = a and x2 = -a; y1 = b and y2 = -b
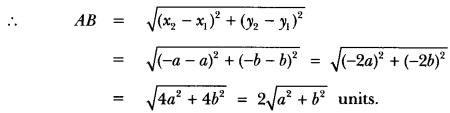
Question 3.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for
your answer: (i) (-1, -2), (1, 0), (- 1, 2), (-3, 0) (ii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution:
(i) Let A(-1, -2), B(1, 0), C(-1, 2) and D(-3, 0) be the four given points.
Then, using distance formula, we have,
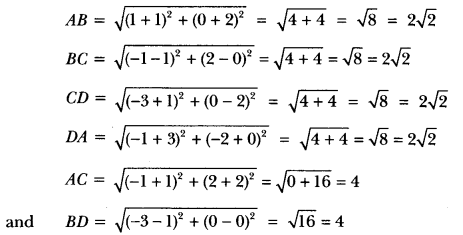
Hence, four sides of quadrilateral are equal and diagonals AC and BD are also equal.
∴ Quadrilateral ABCD is a square.
(ii) Let A (4, 5), B (7, 6), C (4, 3) and D (1, 2) be the given points. Then,
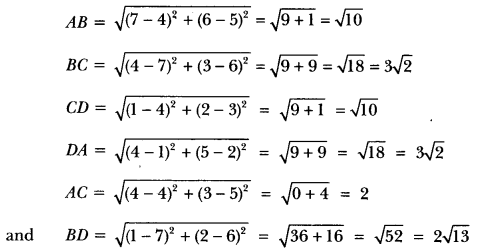
∴ ABCD is a parallelogram.
Question 4.
Find the value of y for which the distance between the points P(2, -3) and Q(10, y) is 10 units.
OR
A line segment is of length 10 units. If the coordinates of its one end are (2, -3) and the abscissa of the other end is 10, find its ordinate.
Solution:
We have, PQ = 10
![]()
Squaring both sides, we have
⇒ (8)2 + (y + 3)2 = 100
⇒ (y + 3)2 = 100 – 64
⇒ (y + 3)2 = 36 or y + 3 ± 16
⇒ y + 3 = 6, y + 3 = -6 or y = 3, y = -9
Hence, values of y are – 9 and 3.
Question 5.
If Q(0, 1) is equidistant from P(5,-3) and R(x, 6) find the value of x. Also, find the distances of QR and PR.
Solution:
Since, point Q(0, 1) is equidistant from P(5, -3) and R(x, 6).
Therefore, QP = QR
Squaring both sides, we have, Qp2 = QR2
⇒ (5 – 0)2 + (-3 -1)2 = (x – 0)2 + (6 – 1)2
25 + 16 = x2 + 25
x2 = 16
∴ x = ±4
Thus, R is (4, 6) or (-4, 6).
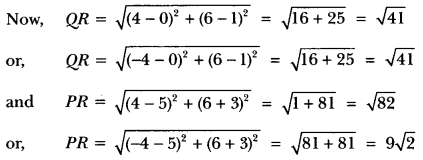
Question 6.
Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).
OR
Find the coordinates of a point on the x-axis which is equidistant from the points A(2, -5) and B(-2, 9).
Solution:
Let P(x, 0) be any point on x-axis.
Now, P(x, 0) is equidistant from point A(2,-5) and B(-2, 9)
∴ AP = BP
![]()
Squaring both sides, we have
(x – 2)2 + 25 = (x + 2)2 + 81
⇒ x2 + 4 – 4x + 25 = x2 + 4 + 4x + 81
⇒ -8x = 56
∴ x = \(\frac{56}{-8}\)
∴ The point on the x-axis equidistant from given points is (-7,0).
Question 7.
Find the relation between x and y, if the points (x, y), (1, 2) and (7, 0) are collinear.
Solution:
Given points are A(x, y), B(1, 2) and C(7, 0)
These points will be collinear if the area of the triangle formed by them is zero.
Now, ar(∆ABC) = \(\frac{1}{2}\) [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
⇒ 0 = \(\frac{1}{2}\) [x(2 – 0) + 1(0 – y) + 7(y – 2)]
⇒ 0 = \(\frac{1}{2}\) (2x – y + 7y – 14)
⇒ 2x + by – 14 = 0
⇒ x + 3y = 7, which is the required relation between x and y.
Question 8.
Find a relation between x and y such that the point (x, y) is equidistant from the point (3,6) and (-3, 4).
Solution:
Let P(x, y) be equidistant from the points A(3, 6) and B(-3, 4)
i.e., PA = PB
Squaring both sides, we get
AP2 = BP2
⇒ (x – 3)2 + (y – 6)2 = (x + 3)2 + (1 – 4)2
⇒ x2 – 6x + 9 + y2 – 12y + 36 = x2 + 6x + 9 +y2 – 8y + 16
⇒ -12x – 4y + 20 = 0
⇒ 3x + y – 5 = 0, which is the required relation.
Question 9.
Find the coordinates of the point which divides the line joining of (- 1, 7) and (4, – 3) in the ratio 2 : 3.
Solution:
Let P(x, y) be the required point. Thus, we have
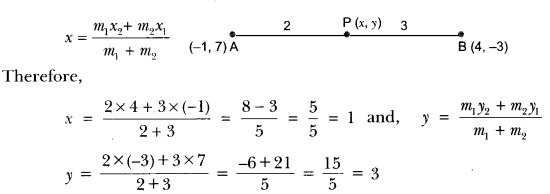
So, the coordinates of P are (1, 3).
Question 10.
Find the coordinates of the points of trisection of the line segment joining (4, – 1) and (-2,-3).
Solution:
Let the given points be A(4, -1) and B(-2,-3) and points of trisection be P and Q.

Lęt AP = PQ = QB = k
PB = PQ + QB = k + k = 2k
AP : PB = k : 2k = 1 : 2.
Therefore, coordinates of P are
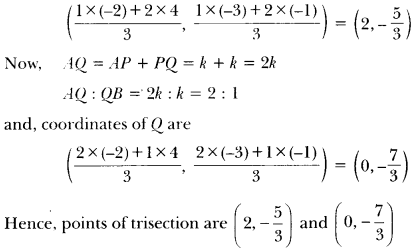
Question 11.
Find the ratio in which the line segment joining A(1, -5) and B(-4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
Solution:
Let the required ratio bek: 1. Then, the coordinates of the point of division is
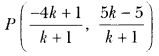
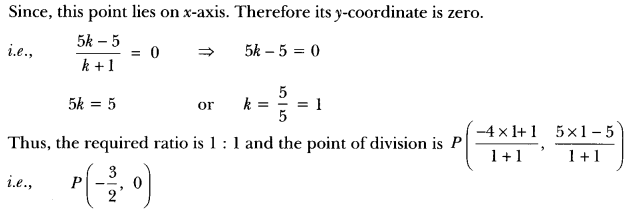
Question 12.
The points A(4, -2), B(7, 2), C(0, 9) and D(-3, 5) form a parallelogram. Find the length of the altitude of the parallelogram on the base AB.
Solution:
Let, DE = h be the height of parallelogram ABCD w.r.t. base AB.

Question 13.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
Solution:
Let the coordinates of A be (x, y)
Now, C is the centre of circle therefore, the coordinates of
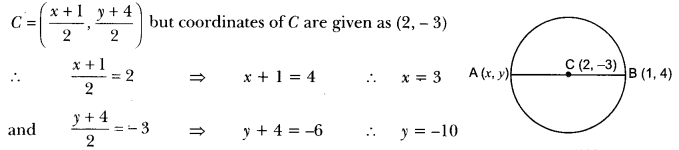
Hence, coordinates of A are (3, -10).
Question 14.
If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AB = 5 AB and P lies on the line segment AB.
Solution:
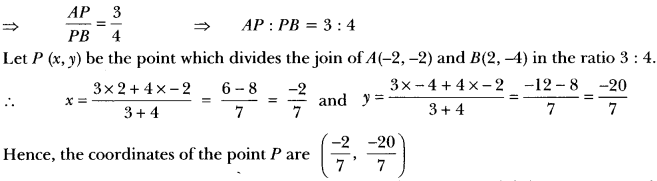
Question 15.
Find the coordinates of the points which divide the line segment joining A (-2, 2) and B (2, 8) into four equal parts (Fig. 6.21).
Solution:
Let P, Q, R be the points that divide the line segment joining A(-2, 2) and B(2, 8) into four equal parts.

Since, Q divides the line segment AB into two equal parts, i.e., Q is the mid-point of AB.
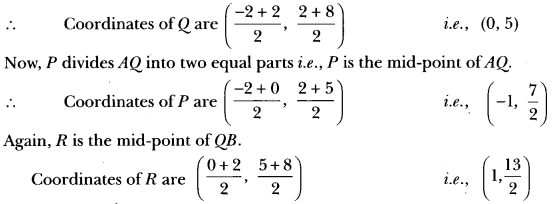
Question 16.
Find the area of a rhombus if its vertices (3, 0), (4, 5), (- 1, 4) and (-2, – 1) are taken in order.
Solution:
Let A(3, 0), B(4, 5), C(-1, 4) and D(-2, -1) be the vertices of a rhombus.
Therefore, its diagonals
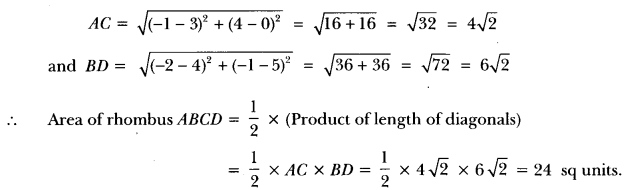
Question 17.
Find the area of the triangle whose vertices are: (-5, -1), (3, -5), (5, 2)
Solution:
Let A(x1, y1) = (-5, -1), B(x2, y2) = (3 – 5), C(x3, y3) = (5, 2)
∴ area of ∆ABC = \(\frac{1}{2}\) [x1 (y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= \(\frac{1}{2}\)(-5(-5 – 2) + 3 (2 + 1) + 5(-1 + 5)]
= \(\frac{1}{2}\)(35 + 9 + 20) = \(\frac{1}{2}\) × 64 = 32 sq units.
Question 18.
If the point A (0, 2) is equidistant from the points B(3, p) and C(p, 5), find p. Also find the length of AB.
Solution:
Given that A (0, 2) is equidistant from B (3, p) and C (p, 5)
∴ AB = AC
or
AB2 = AC2
(3 – 0)2 + (0 – 2)2 = (p – 0)2 + (5 – 2)2
32 + p2 + 4 – 4p = p2 + 9
= 4 – 4p = 0
⇒ 4p = 4
⇒ p = 1
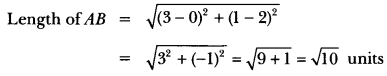
Question 19.
If the points A (-2, 1), B (a, b) and C (4, -1) are collinear and a – b = 1, find the values of a and b.
Solution:
Since the given points are collinear, then area of ∆ABC = 0
⇒ \(\frac{3}{5}\)[x1 ( y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 0
Given, x1 = -2, y1 = 1, x2 = 0, y2 = b, x3 = 4, y3 = -1
Putting the values,
\(\frac{1}{2}\)[-2(b + 1) + a(-1 – 1) + 4(1 – b)] = 0
⇒ -26 – 2 – 2a + 4- 4b = 0
⇒ 2a + 65 = 2
a + 3b = 1 ….. (i)
Given, a – b = 1 … (ii)
Subtracting (i) from (ii), we have
– 4b = 0
⇒ b = 0
Substituting the value of b in (ii), we have a = 1.
Question 20.
If the point P (k-1, 2) is equidistant from the points A (3, k) and B (k, 5), find the values of k.
Solution:
Let the given line segment be divided by point Q. Since P is equidistant from A and B,
AP = BP or Ap2 = BP2
[3 – (k – 1)]2 + (k – 2)2 = [k – (k – 1)]2 + (5 – 2)2
(3 – k + 1)2 + (k – 2)2 = (k – k + 1)2 + (3)2
(4 – k)2 + (k – 2)2 = (1)2 + (3)2
⇒ 16 + k2 – 8k + k2 + 4 – 4k = 1 + 9
⇒ 2k2 – 12k + 20 = 10
⇒ k2 – 6k + 10 = 5
⇒ ķ2 – 6k + 5 = 0
⇒ k2 – 5k – k + 5 = 0
⇒ k (k – 5) -1(k – 5) = 0
⇒ k = 1 or k = 5
Question 21.
Find the ratio in which the line segment joining the points A(3, -3) and B(-2, 7) is divided by x-axis. Also find the coordinates of the point of division.
Solution:
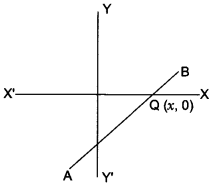
Here, point Q is on x-axis so its ordinate is O.
Let ratio be k : 1 and coordinate of point Q be (x, 0)
![]()
We are given that A(3, -3) and B(-2, 7)

Question 22.
Find the values of k if the points Ask + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear.
Solution:
Points Ask + 1, 2k), B (3k, 2k + 3) and C (5k – 1, 5k) are collinear
∴ Area of ∆ABC = 0
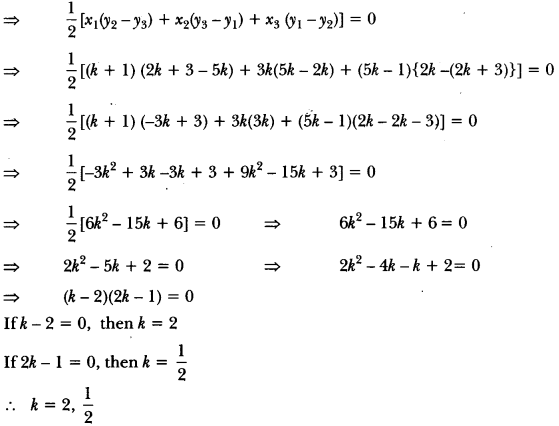
Question 23.
If the point P(x, y) is equidistant from the points A(a + b, b – a) and B(a – b, a + b). Prove that bx = ay.
Solution:
Given, PA = PB or (PA)2 = (PB)2
(a + b – x)2 + (b – a – y)2 = (a – b – x)2 + (a + b – y)2
⇒ (a + b)2 + x2 – 2ax – 25x + (b – a)2 + y2 – 2by + 2ay
⇒ (a – b)2 + x2 – 2ax + 2bx + (a + b)2 + y2 – 2ay – 2by
⇒ 4ay = 4bx or bx = ay
Hence proved.
Question 24.
If the point C(-1, 2) divides internally the line segment joining the points A(2, 5) and B(x, y) in the ratio of 3 : 4, find the value of x2 + y2.
Solution:
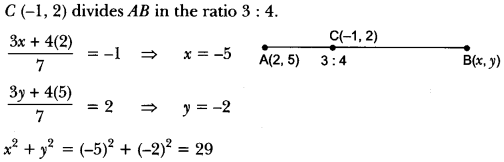
Question 25.
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.
Solution:
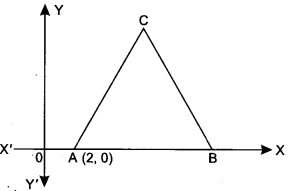
Since AB = BC = AC = 3 units
∴ Co-ordinates of B are (5, 0)
Let co-ordinates of C be (x, y)
AC2 = BC2
[∵ ∆ABC is an equilateral triangle]
Using distance formula
⇒ (x – 2)2 + (y – 0)2 = (x – 5)2 + (y – 0)2
⇒ x2+ 4 – 4x + y = x2+ 25 – 10x + y2 6x = 21
⇒ x = \(\frac{21}{6}\) = \(\frac{7}{2}\)
Again (x – 2)2 + (y – 0)2 = 9
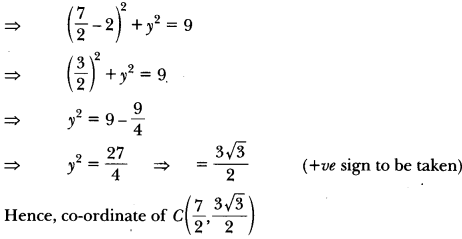
Coordinate Geometry Class 10 Extra Questions Long Answer Type
Question 1.
Find the value of ‘k”, for which the points are collinear: (7, -2), (5, 1), (3, k).
Solution:
Let the given points be
A (x1, y1) = (7, -2), B (x2, Y2) = (5, 1) and C (x3, y3) = (3, k)
Since these points are collinear therefore area (∆ABC) = 0
⇒ \(\frac{1}{2}\) [x1(y2 – Y3) + x2(y3 – y1) + x3(y1 – y2)] = 0
⇒ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) = 0
⇒ 7(1 – k) + 5(k + 2) + 3(-2 -1) = 0
⇒ 7 – 7k + 5k + 10 – 9 = 0
⇒ -2k + 8 = 0
⇒ 2k = 8
⇒ k = 4
Hence, given points are collinear for k = 4.
Question 2.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Solution:
Let A (x1, y1) = (0, -1), B (x2, y2) = (2, 1), C (x3, y3) = (0, 3) be the vertices of ∆ABC.
Now, let P, Q, R be the mid-points of BC, CA and AB, respectively.
So, coordinates of P, Q, R are
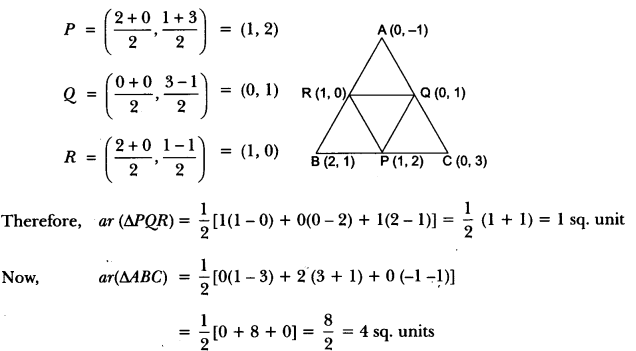
Ratio of ar (∆PQR) to the ar (∆ABC) = 1 : 4.
Question 3.
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Solution:
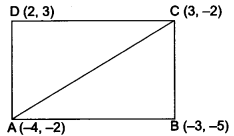
Let A(4, -2), B(-3, -5), C(3, -2) and D(2, 3) be the vertices of the quadrilateral ABCD.
Now, area of quadrilateral ABCD
= area of ∆ABC + area of ∆ADC
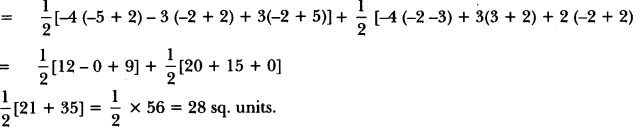
Question 4.
A median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ABC whose vertices are A (4,-6), B (3, -2) and C (5, 2).
Solution:
Since AD is the median of ∆ABC, therefore, D is the mid-point of BC.

Hence, the median divides it into two triangles of equal areas.
Question 5.
Find the ratio in which the point P (x, 2), divides the line segment joining the points A (12, 5) and B (4, -3). Also find the value of x.
Solution:

The ratio in which p divides the line segment is \(\frac{3}{5}\), i.e., 3 : 5.
Question 6.
If A (4, 2), B (7, 6) and C (1, 4) are the vertices of a ∆ABC and AD is its median, prove that the median AD divides into two triangles of equal areas.
Solution:
Given: AD is the median on BC.
⇒ BD = DC
The coordinates of midpoint D are given by.

Hence, AD divides ∆ABC into two equal areas.
Question 7.
If the point A (2, -4) is equidistant from P (3, 8) and Q (-10, y), find the values of y. Also find distance PQ.
Solution:
Given points are A(2, 4), P(3, 8) and Q(-10, y)
According to the question,
PA = QA
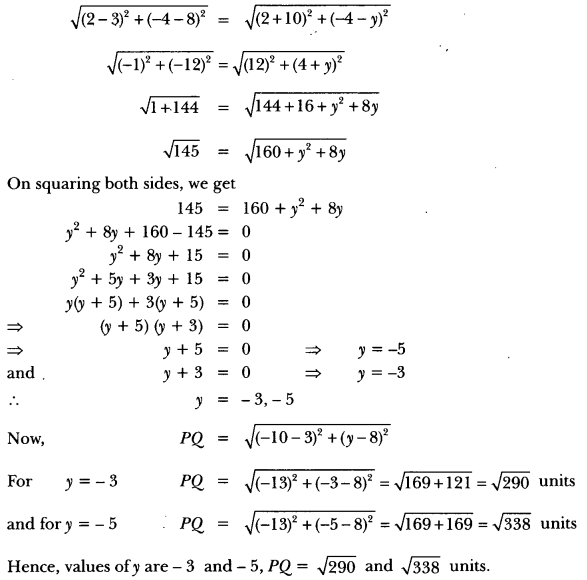
Question 8.
The base BC of an equilateral triangle ABC lies on y-axis. The coordinates of point Care (0, -3). The origin is the mid-point of the base. Find the coordinates of the points A and B. Also find the coordinates of another point D such that BACD is a rhombus.
Solution:
∵ O is the mid-point of the base BC.
∴ Coordinates of point B are (0, 3). So,
BC = 6 units Let the coordinates of point A be (x, 0).
Using distance formula,

∴ Coordinates of point A = (x, 0) = (3√3, 0)
Since BACD is a rhombus.
∴ AB = AC = CD = DB
∴ Coordinates of point D = (-3√3, 0).
Question 9.
Prove that the area of a triangle with vertices (t, t-2), (t + 2, t + 2) and (t + 3, t) is independent of t.
Solution:
Area of a triangle = \(\frac{1}{2}\) [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
Area of the triangle = \(\frac{1}{2}\)[t + 2 – t) + (t + 2) (t – t + 2) + (t + 3) (t – 2 – t – 2)]
= \(\frac{1}{2}\) [2t + 2t + 4 – 4t – 12 ]
= 4 sq. units
which is independent of t.
Hence proved.
Question 10.
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, -2). If the third vertex is (\(\frac{7}{2}\), y), find the value of y.
Solution:
Given: ar(∆ABC) = 5 sq. units
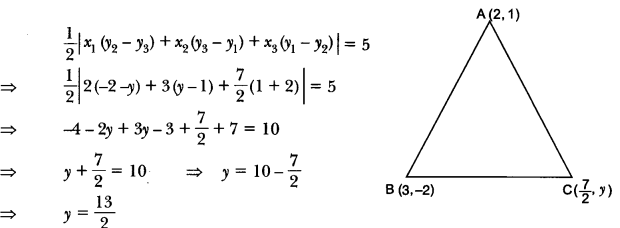
Question 11.
The coordinates of the points A, B and Care (6, 3), (-3,5) and (4,-2) respectively. P(x, y) is any point in the plane. Show that \(\frac { ar(∆PBC) }{ ar(∆ABC) } \) = \(\frac{x+y-2}{7}\)
Solution:
P(x, y), B(-3, 5), C(4, -2), A(6, 3)
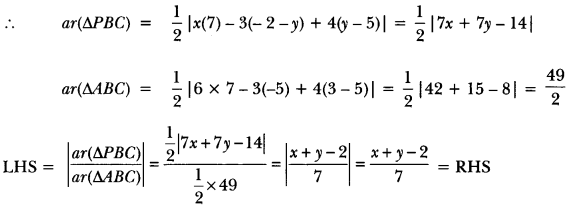
Question 12.
In Fig. 6.32, the vertices of ∆ABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that \(\frac{A D}{A B}=\frac{A E}{A C}=\frac{1}{3}\) Calculate the area of ∆ADE and compare it with area of ∆ABC.
Solution:
\
Question 13.
If a = b = 0, prove that the points (a, a2), (b, b2) (0, 0) will not be collinear.
Solution:
∵ We know that three points are collinear if area of triangle = 0
∴ Area of triangle with vertices (a, a2), (b, b2) and (0, 0)
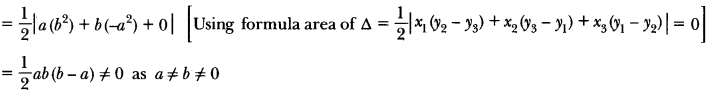
∵ Area of ∆ ≠ 0
∴ Given points are not collinear.
Coordinate Geometry Class 10 Extra Questions HOTS
Question 1.
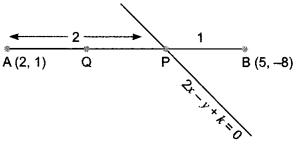
The line joining the points (2, 1) and (5, -8) is trisected by the points P and Q. If the point P lies on the line 2x – y + k = 0, find the value of k.
Solution:
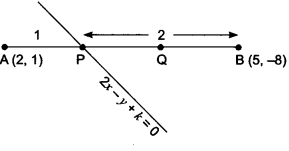
As line segment AB is trisected by the points P and Q.
Therefore,
Case I: When AP : PB = 1 : 2.
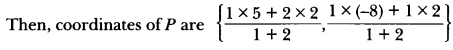
⇒ P (3, -2)
Since the point P (3,-2) lies on the line
2x – y + k = 0 =
⇒ 2 × 3-(-2) + k = 0
⇒ k = -8
Case II: When AP : PB = 2 : 1.
Coordinates of point P are
![]()
Since the point P(4, -5) lies on the line
2x – y + k = 0
∴ 2 × 4-(-5) + k = 0
∴ k = -13
Question 2.
Prove that the diagonals of a rectangle bisect each other and are equal.
Solution:
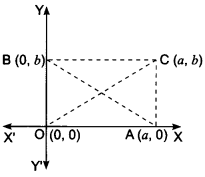
Let OACB be a rectangle such that OA is along x-axis and OB is along y-axis. Let OA = a and OB = b.
Then, the coordinates of A and B are (a,0) and (0, b) respectively.
Since, OACB is a rectangle. Therefore,
AC = OB
⇒ AC = b
Also, OA = a
⇒ BC = a
So, the coordinates of Care (a, b).

∴ OC = AB.
Question 3.
In what ratio does the y-axis divide the line segment joining the point P (4, 5) and Q (3, -7)?
Also, find the coordinates of the point of intersection.
Solution:
Suppose y-axis divides PQ in the ratio k : 1. Then, the coordinates of the point of division are|

Question 4.
Find the centre of a circle passing through the points (6, -6), (3, -7) and (3, 3).
Solution:
Let O(x, y) be the centre of circle. Given points are A(6, -6), B(3, -7) and C(3, 3).

Question 5.
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, – 3) and (3, 4). Find its centroid.
Solution:
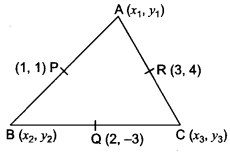
Let P(1, 1), Q(2, -3), R(3, 4) be the mid-points of sides AB, BC and CA respectively, of triangle ABC. Let A(x1, y1), B(x2, y2) and C(x3, y3) be the vertices of triangle ABC. Then, P is the mid-point of AB.
Question 6.
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, -2) and B(3, 7).
Solution:
Let P(x1, y1) be common point of both lines and divide the line segment joining A(2, -2) and B(3, 7) in ratio k : 1.
Question 7.
Show that ∆ABC with vertices A (-2, 0), B (2, 0) and C (0, 2) is similar to ∆DEF with vertices
D(4, 0) E (4, 0) and F (0, 4).
Solution:
Given vertices of ∆ABC and ∆DEF are
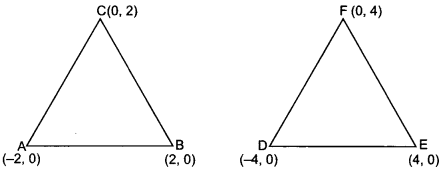
A(-2, 0), B(2, 0), C(0, 2), D(-4, 0), E(4, 0) and F(0, 4)
![]()
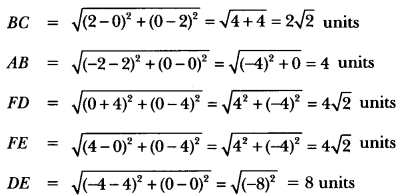
Here, we see that sides of ∆DEF are twice the sides of a ∆ABC.
Hence, both triangles are similar.
