
On this page, you will find Coordinate Geometry Class 9 Notes Maths Chapter 6 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 6 Coordinate Geometry will seemingly help them to revise the important concepts in less time.
CBSE Class 9 Maths Chapter 6 Notes Coordinate Geometry
Coordinate Geometry Class 9 Notes Understanding the Lesson
Rene Descartes was a French mathematician. He introduced an idea of Carterian Coordinate System for describing the position of a point in a plane. The idea which has given rise to an important branch of Mathematics known as Coordinate Geometry.
1. Cartesian coordinate system: A system which describe the position of a point in a plane is called Cartesian system.
2. Cartesian coordinate axis: Let us draw a horizontal line XX’ and a vertical line YY’ in a plane. Both the lines intersect each other at 90°, then the plane is divided into four parts.
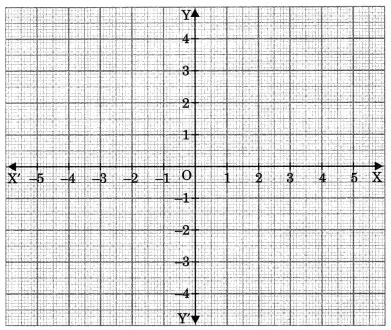
The lines XX’ and YY’ are called axes i.e., XX’ is the x-axis and YY’ is y-axis.
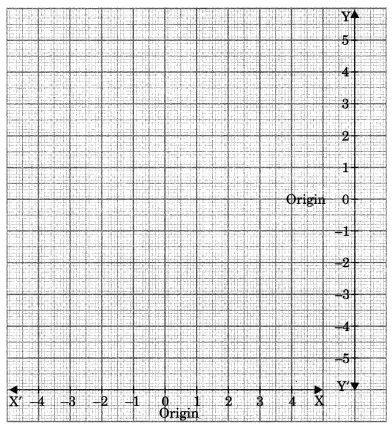
3. Origin: The point where both the axis intersect each other is known as origin.
4. Quadrant
When XX’ and YY’ intersect each other then the plane is divided into four parts. These parts are called quadrants. The plane is known as Cartesian plane or XY plane.
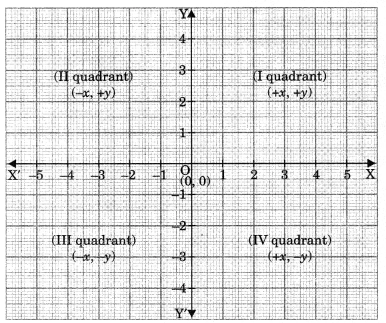
5. Coordinate Geometry: It is a branch of geometry in which geometric problems are solved through algebra by using coordinate system.
6. Cartesian Coordinate (Rectangular Coordinate) System
In this system, the position of a point P is determined by knowing the distances from two perpendicular lines passing through the fixed point O is called origin.
The position of the point P from origin on x-axis is called x-coordinate and the position of P from origin on y-axis is called y-coordinate.
Abscissa: The distance of a point P from y-axis is called abscissa.
Ordinate: The distance of a point P from x-axis is called its ordinate.
Abscissa and ordinate together determine the position of a point in a plane, and it is called coordinates of the point. If a and b are respectively abscissa and ordinate, then the coordinates are (a, b).
Note:
- In first quadrant values of x and y are both positive.
- In second quadrant value of x is negative whereas the value of y is positive.
- In third quadrant value of x and y both are negative.
- In fourth quadrant, the value of x is positive and value ofy is negative.
- Perpendicular distance of a point from x-axis = (+)y-coordinate.
- Perpendicular distance of a point from y-axis = (+)x-coordinate.
- A point which lies on x-axis has coordinates of the form (a, 0).
- A point which lies on y-axis has coordinates of the form (0, b).
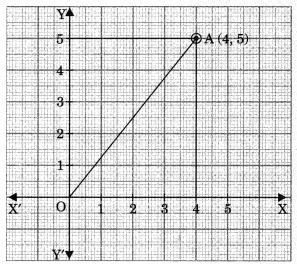
- Distance of a point P(x, y) from origin 0(0, 0) =\(\sqrt{x^{2}+y^{2}}\)
e.g., distance of a point A(4,5) from origin, OA = \(\sqrt{4^{2}+5^{2}}\)
\(=\sqrt{16+25}=\sqrt{41}\)units