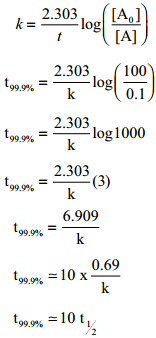Half Life Period of a Reaction

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Half Life Period of a Reaction

The half life of a reaction is defined as the time required for the reactant concentration to reach one half its initial value. For a first order reaction, the half life is a constant i.e., it does not depend on the initial concentration.

The rate constant for a first order reaction is given by

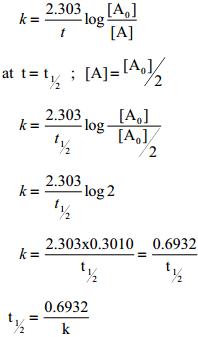
Let us calculate the half life period for a zero order reaction.

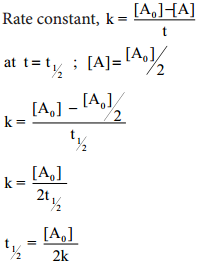
Hence, in contrast to the half life of a first order reaction, the half life of a zero order reaction is directly proportional to the initial concentration of the reactant.

Example 1

A first order reaction takes 8 hours for 90% completion. Calculate the time required for 80% completion. (log 5 = 0.6989; log 10 = 1)
Solution:
For a first order reaction
k = \(\frac{2.303}{t}\)log[latex]\frac{\left[\mathrm{A}_{0}\right]}{[\mathrm{A}]}[/latex] …………. (1)
Let [A_°] = 100M
When t = t_90%; [A]=10M (given that t_90% = 8hours)
t = t_90%; [A]=20M

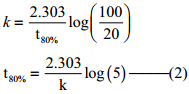
Find the value of k using the given data

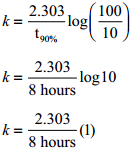
Substitute the value of k in equation (2)

t_80% = \(\frac{2.303}{2.303/8hours}\) log(5)
t_80% = 8hours × 0.6989
t_80% = 5.59hours

Example 2

The half life of a first order reaction x → products is 6.932 × 10⁴s at 500k. What percentage of x would be decomposed on heating at 500K for 100 min.(e^0.06=1.06).
Solution:
Given t_1/2 = 0.6932 × 10⁴s
\(\frac{\left[\mathrm{A}_{0}\right]-[\mathrm{A}]}{\left[\mathrm{A}_{0}\right]}\) × 100
We know that
For a first order reaction, t_1/2 = \(\frac{0.6932}{k}\)

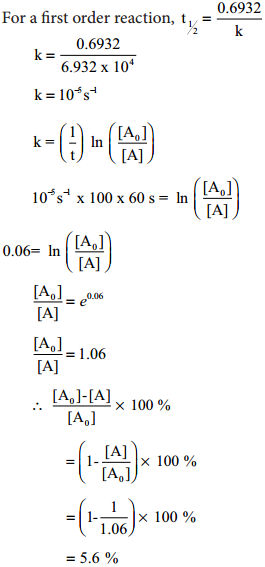
Example 3

Show that case of first order reaction, the time required for 99.9% completion is nearly ten times the time required for half completion of the reaction.
Solution:
Let [A_°] = 100
When t = t_99.9%; [A] = (100 – 99.9) = 0.1