Here we are providing Introduction to Euclid’s Geometry Class 9 Extra Questions Maths Chapter 5 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-9-maths/
Extra Questions for Class 9 Maths Introduction to Euclid’s Geometry with Answers Solutions
Extra Questions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry with Solutions Answers
Introduction to Euclid’s Geometry Class 9 Extra Questions Very Short Answer Type
Class 9 Maths Chapter 5 Extra Questions With Solutions Question 1.
Give a definition of parallel lines. Are there other terms that need to be defined first ? What are they and how might you define them?
Solution:
Two coplanar lines in a plane) which are not intersecting are called parallel lines. The other term intersecting is undefined.
Introduction To Euclidean Geometry Class 9 Extra Questions Question 2.
Give a definition of perpendicular lines. Are there other terms that need to be defined first ? What are they and how might you define them?
Solution:
Two coplanar (in a plane) lines are perpendicular if the angle between them at the point
of intersection is one right angle. The other terms point of intersection and one right angle are undefined.
Euclid’s Geometry Class 9 Extra Questions Question 3.
Give a definition of line segment. Are there other terms that need to be defined first ? What are they and how might you define them ?
Solution:
A line segment PQ of a line ‘l is the continuous part of the line I with end points P and Q.
![]()
Here, continuous part of the line ‘l is undefined.
Euclid’s Geometry Class 9 Extra Questions With Solutions Question 4.
Solve the equation a – 15 = 25 and state which axiom do you use here.
Solution:
a – 15 = 25
On adding 15 to both sides, we obtain
a – 15 + 15 = 25 + 15 [using Euclid’s second axiom]
a = 40
Questions On Euclid Geometry Class 9 Question 5.
Ram and Ravi have the same weight. If they each gain weight by 2 kg, how will their new weights be compared ?
Solution:
Let x kg be the weight each of Ram and Ravi.
On adding 2 kg,
Weight of Ram and Ravi will be (x + 2) kg each.
According to Euclid’s second axiom, when equals are added to equals, the wholes are equal.
So, weight of Ram and Ravi are again equal.
Chapter 5 Maths Class 9 Extra Questions Question 6.
If a point C be the mid-point of a line segment AB, then write the relation among AC, BC and AB.
Solution:
Here, C is the mid-point of AB
⇒ AC = BC
⇒ AC = BC = \(\frac{1}{2}\)AB
![]()
Euclid Geometry Class 9 Questions And Answers Question 7.
If a point P be the mid-point of MN and C is the mid-point of MP, then write the relation between MC and MN.
Solution:
Here, P is the mid-point of MN and C is the mid-point of MP.
![]()
∴ MC = \(\frac{1}{4}\)MN
Extra Questions For Class 9 Maths Chapter 5 Question 8.
How many lines does pass through two distinct points ?
Solution:
One and only one.
Euclid Geometry Class 9 Questions Question 9.
In the given figure, if AB = CD, then prove that AC = BD. Also, write the Euclid’s axiom used for proving it.
![]()
Solution:
Here, given that
AB = CD
By using Euclid’s axiom 2, if equals are added to equals, then the wholes are equal, we have
AB + BC = CD + BC
⇒ AC = BD
Introduction to Euclid’s Geometry Class 9 Extra Questions Short Answer Type 2
Euclids Geometry Class 9 Extra Questions Question 1.
Define :
(a) a square (b) perpendicular lines.
Solution:
(a) A square : A square is a rectangle having same length and breadth. Here, undefined terms are length, breadth and rectangle.
(b) Perpendicular lines : Two coplanar (in a plane) lines are perpendicular, if the angle between them at the point of intersection is one right angle. Here, the term one right angle is undefined.
Class 9 Maths Chapter 5 Important Questions Question 2.
In the given figure, name the following :
(i) Four collinear points
(ii) Five rays
(iii) Five line segments
(iv) Two-pairs of non-intersecting line segments.
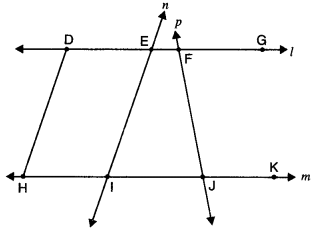
Solution:
(i) Four collinear points are D, E, F, G and H, I, J, K
(ii) Five rays are DG, EG, FG, HK, IK.
(iii) Five line segments are DH, EI, FJ; DG, HK.
(iv) Two-pairs of non-intersecting line segments are (DH, EI) and (DG, HK).
Class 9 Maths Chapter 5 Extra Questions Question 3.
In the given figure, AC = DC and CB = CE. Show that AB = DE. Write the Euclid’s axiom to support this.
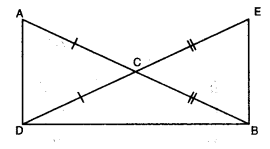
Solution:
We have
AC = DC
CB = CE
By using Euclid’s axiom 2, if equals are added to equals, then wholes are equal.
⇒ AC + CB = DC + CE
⇒ AB = DE.
Question 4.
In figure, it is given that AD=BC. By which Euclid’s axiom it can be proved that AC = BD?
![]()
Solution:
We can prove it by Euclid’s axiom 3. “If equals are subtracted from equals, the remainders are equal.”
We have AD = BC
⇒ AD – CD = BC – CD
⇒ AC = BD
Question 4.
If A, B and C are any three points on a line and B lies between A and C (see figure), then prove that AB + BC = AC.
![]()
Solution:
In the given figure, AC coincides with AB + BC. Also, Euclid’s axiom 4, states that things
which coincide with one another are equal to one another. So, it is evident that:
AB + BC = AC.
Question 5.
In the given figure, AB = BC, BX = BY, show that
AX = CY.
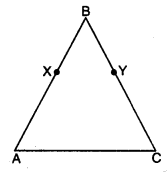
Solution:
Given that AB = BC
and BX = BY
By using Euclid’s axiom 3, equals subtracted from equals, then the remainders are equal, we have
AB – BX = BC – BY
AX = CY
Question 6.
![]()
In the above figure, if AB = PQ, PQ = XY, then AB = XY. State True or False. Justify your answer.
Solution:
True. ∵ By Euclid’s first axiom “Things which are equal to the same thing are equal to one another”.
∴ AB = PQ and XY = PQ ⇒ AB = XY
Question 7.
In the given figure, if ∠1 = ∠3, ∠2 = ∠4 and ∠3 = ∠4, write the relation between ∠1 and ∠2, using an Euclid’s axiom.
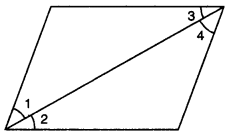
Solution:
Here, ∠3 = ∠4, ∠1 = ∠3 and ∠2 = ∠4. Euclid’s first axiom says, the things which are equal to equal thing are equal to one another. So ∠1 = ∠2.,
Question 8.
In the given figure, we have ∠1 = ∠2, ∠3 = ∠4. Show that ∠ABC = ∠DBC. State the Euclid’s Axiom used.
Solution:
Here, we have 1 = ∠2 and ∠3 = ∠4. By using Euclid’s Axiom 2. If equals are added to
equals, then the wholes are equal..
∠1 + ∠3 = ∠2 + ∠4
∠ABC = ∠DBC.
Question 9.
In the figure, we have BX and \(\frac{1}{2}\) AB =\(\frac{1}{2}\) BC. Show that BX = BY.
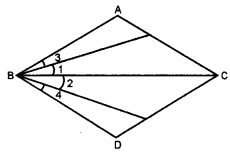
Solution:
Here, BX = \(\frac{1}{2}\) AB and BY = \(\frac{1}{2}\) BC …(i) [given]
Also, AB = BC [given]
⇒ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)BC …(ii)
[∵ Euclid’s seventh axiom says, things which are halves of the same thing are equal to one another]
From (i) and (ii), we have BX = BY
Question 10.
In the given figure, AC = XD, C is mid-point of AB and D is mid-point of XY. Using an Euclid’s axiom, show that AB = XY.
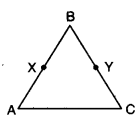
Solution:
∵ C is the mid-point of AB
AB = 2AC
Also, D is the mid-point of XY
XY = 2XD
By Euclid’s sixth axiom “Things which are double of same things are equal to one another.”
∴ AC = XD = 2AC = 2XD ⇒ AB = XY
Introduction to Euclid’s Geometry Class 9 Extra Questions HOTS
Question 1.
For given four distinct points in a plane, find the number of lines that can be drawn through :
(i) When all four points are collinear.
(ii) When three of the four points are collinear.
(iii) When no three of the four points are collinear.
Solution:
![]()
(i) Consider the points given are A, B, C and D.
When all the four points are collinear :
One line \(\overrightarrow{\mathrm{AD}}\).
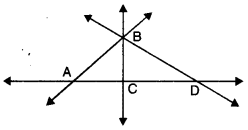
(ii) When three of the four points are collinear :
4 lines
Here, we have four lines \(\stackrel{\leftrightarrow}{A B}, \stackrel{\leftrightarrow}{B C}, \stackrel{\leftrightarrow}{B D}, \stackrel{\leftrightarrow}{A D}\) (four).
(iii) When no three of the four points are collinear :
6 lines Here, we have
\(\stackrel{\leftrightarrow}{A B}, \stackrel{\leftrightarrow}{B C}, \stackrel{\leftrightarrow}{A C}, \stackrel{\leftrightarrow}{A D}, \stackrel{\leftrightarrow}{B D}, \stackrel{\leftrightarrow}{C D}\) (six).
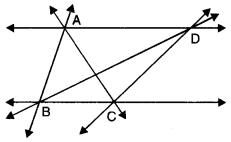
Question 2.
Show that : length AH > sum of lengths of AB + BC + CD.
![]()
Solution:
We have
AH = AB + BC + CD + DE + EF + FG + GH
Clearly, AB + BC + CD is a part of AH.
⇒ AH > AB + BC + CD
Hence, length AH > sum of lengths AB + BC + CD.
Introduction to Euclid’s Geometry Class 9 Extra Questions Value Based (VBQs)
Question 1.
Rohan’s maid has two children of same age. Both of them have equal number of dresses. Rohan on his birthday plans to give both of them same number of dresses. What can you say about the number of dresses each one of them will have after Rohan’s birthday? Which Euclid’s axiom is used to answer this question? What value is Rohan depicting by doing so ? Write one more Euclid’s axiom.
Solution:
Here, Rohan’s maid has two children of same age group and both of them have equal number of dresses. Rohan on his birthday plans to give both of them same number of dresses.
∴ By using Euclid’s Axiom 2, if equals are added to equals, then the whole are equal. Thus, again both of them have equal number of dresses. Value depicted by Rohan are caring and other social values. According to Euclid’s Axiom 3, if equals are subtracted from equals, then the remainders
are equal.
Question 2.
Three lighthouse towers are located at points A, B and C on the section of a national forest to protect animals from hunters by the forest department as shown in figure. Which value is department exhibiting by locating extra towers ? How many straight lines can be drawn from A to C? State the Euclid Axiom which states the required result. Give one more. Postulate.
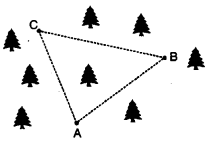
Solution:
One and only one line can be drawn from A to C. According to Euclid’s Postulate, “A straight line may be drawn from any point to any other point:” An other postulate : “A circle may be described with any centre and any radius.” Wildlife is a part of our environment and conservation of each of its element is important for ecological balance.
