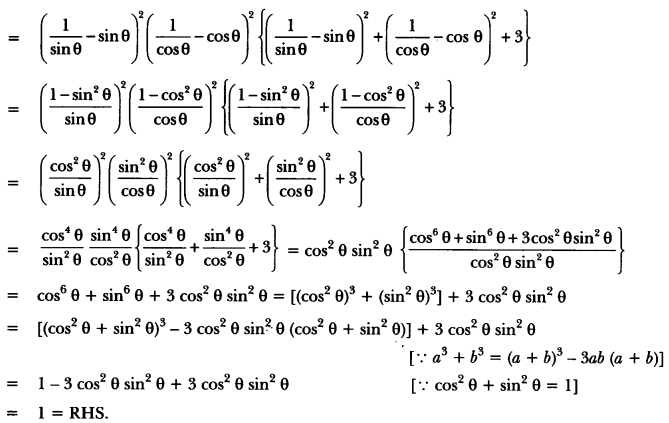Introduction to Trigonometry Class 10 Extra Questions Maths Chapter 8 with Solutions Answers

Here we are providing Introduction to Trigonometry Class 10 Extra Questions Maths Chapter 8 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/

Extra Questions for Class 10 Maths Introduction to Trigonometry with Answers Solutions

Extra Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry with Solutions Answers

Introduction to Trigonometry Class 10 Extra Questions Short Answer Type 1

Trigonometry Class 10 Extra Questions Question 1.
Find maximum value of \(\frac{1}{\sec \theta}\), 0°≤ θ ≤ 90°.
Solution:
\(\frac{1}{\sec \theta}\), (0° ≤ θ ≤ 90°) (Given)
∵ sec θ is in the denominator
∴ The min. value of sec θ will return max. value for \(\frac{1}{\sec \theta}\).
But the min. value of sec θ is sec 0° = 1.
Hence, the max. value of \(\frac{1}{\sec 0^{\circ}}\) = \(\frac{1}{1}\) = 1

Trigonometry Extra Questions Class 10 Question 2.
Given that sin θ = \(\frac{a}{b}\), find the value of tan θ.
Solution:
sin θ = \(\frac{a}{b}\)

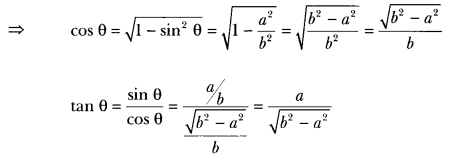
Trigonometry Questions For Class 10 Question 3.
If sin θ = cos θ, then find the value of 2 tan θ + cos² θ.
Solution:
sin θ = cos θ (Given)
It means value of θ = 45°
Now, 2 tan θ + cos² θ = 2 tan 45° + cos² 45°

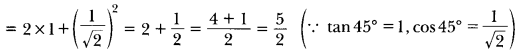
Introduction To Trigonometry Class 10 Extra Questions With Answers Question 4.
If sin (x – 20)° = cos (3x – 10)°, then find the value of x.
Solution:
sin (x – 20)° = cos (3x – 10)°
⇒ cos [90° – (x – 20)°] = cos (3x – 10)°
By comparing the coefficient
90° – x° + 20° = 3x° – 10° = 110° + 10° = 3x° + x°
120° = 4x°
⇒ \(\frac{120^{\circ}}{4}\) = 30°

Class 10 Trigonometry Extra Questions Question 5.
If sin² A = \(\frac{1}{2}\)tan² 45°, where A is an acute angle, then find the value of A.
Solution:
sin²A = \(\frac{1}{2}\)tan² 45°
⇒ sin²A = \(\frac{1}{2}\) (1)² [∵ tan 45° = 1]
= sin² A = \(\frac{1}{2}\)
⇒ sin A = \(\frac{1}{\sqrt{2}}\)
Hence, ∠A = 45°

Extra Questions Of Trigonometry Class 10 Question 6.
If x = a cos θ, y = b sin θ, then find the value of b²x² + a²y² – a²b².
Solution:
Given x = acos θ, y = b sin θ
b²x² + a²y² – a²b² = b²(acos θ)² + a²(b sin θ)² – a²b²
= a²b² cos²θ + a²b² sin² θ – a²b² = a²b² (sin² θ + cos² θ) – a²b²
= a²b² – a²b² = θ (∵ sin² θ + cos² θ = 1)

Trigonometry Class 10 Questions Question 7.
If tan A = cot B, prove that A + B = 90°.
Solution: We have
tan A = cot B
⇒ tan A = tan (90° – B)
A = 90° – B
[∵ Both A and B are acute angles]
⇒ A + B = 90°

Extra Questions On Trigonometry Class 10 Question 8.
If sec A = 2x and tan A = \(\frac{2}{x}\), find the value of 2\(\left(x^{2}-\frac{1}{x^{2}}\right)\) .
Solution:

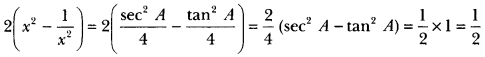
Class 10 Maths Chapter 8 Extra Questions Question 9.
In a ∆ABC, if ∠C = 90°, prove that sin² A + sin² B = 1.
Solution:
Since ∠C = 90°
∴ ∠A + ∠B = 180° – ∠C = 90°
Now, sin² A + sin² B = sin² A + sin² (90° – A) = sin² A + cos² A = 1

Trigonometry Extra Questions Question 10.
If sec 4A = cosec (A – 20°) where 4 A is an acute angle, find the value of A.
Solution:
We have
sec 4 A = cosec (A – 20°)
⇒ cosec (90° – 4 A) = cosec (A – 20°)
∴ 90° – 4 A = A – 20°
⇒ 90° + 20° = A + 4 A
⇒ 110° = 5 A
∴ A = \(\frac{110}{5}\) = 22°

Introduction to Trigonometry Class 10 Extra Questions Short Answer Type 2

Introduction To Trigonometry Class 10 Extra Questions Question 1.
If sin A = \(\frac{3}{4}\), calculate cos A and tan A.
Solution:
Let us first draw a right ∆ABC in which ∠C = 90°.
Now, we know that

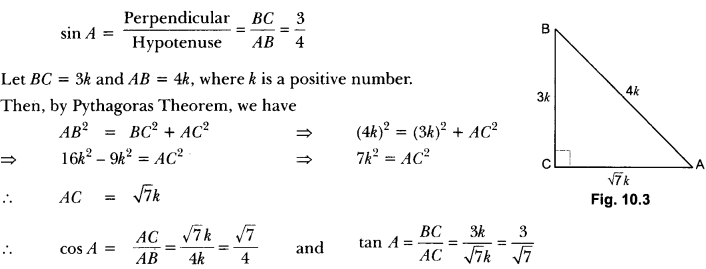
Important Questions For Class 10 Maths Trigonometry With Solutions Question 2.
Given 15 cot A = 8, find sin A and sec A.
Solution:
Let us first draw a right ∆ABC in which ∠B = 90°.
Now, we have, 15 cot A = 8

Trigonometry Class 10 Extra Questions With Solutions Question 3.
In Fig. 10.5, find tan P – cot R.
Solution:

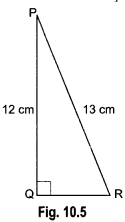
Using Pythagoras Theorem, we have
PR² = PO² + QR²
⇒ (13)² = (12)² + QR²
⇒ 169 = 144 + QR²
⇒ QR² = 169 – 144 = 25
⇒ QR = 5 cm
Now, tan P = \(\frac{QR}{PQ}\) = \(\frac{5}{12}\) and cot R = \(\frac{QR}{PQ}\) = \(\frac{5}{12}\)
tan P – cot R = \(\frac{5}{12}\) – \(\frac{5}{12}\) = 0

Class 10 Maths Trigonometry Extra Questions Question 4.
If sin θ + cos θ = √3 , then prove that tan θ + cot θ = 1.
Solution:
sin θ + cos θ = √3
⇒ (sin θ + cos θ)² = 3
⇒ sin² θ + cos² θ + 2 sin θ cos θ = 3
⇒ 2 sin cos θ = 2 (∵ sin² θ + cos² θ = 1)
⇒ sin θ. cos θ = 1 = sin² θ + cos² θ

⇒ 1 = tan θ + cot θ = 1
Therefore tan θ + cot θ = 1

Extra Question Of Trigonometry Class 10 Question 5.
Prove that \(\frac { 1-sinθ }{ 1+sinθ } \) = (sec θ – tan θ)²
Solution:

Without using tables, evaluate the following (6 to 10).

Question 6.

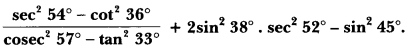
Solution:

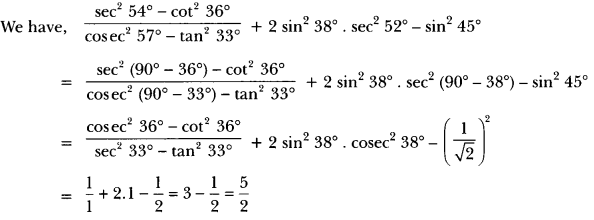
Trigonometry Important Questions Class 10 Question 7.

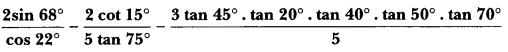
Solution:

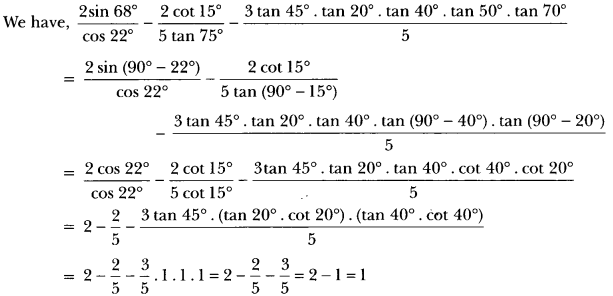
Extra Questions On Introduction To Trigonometry Class 10 Question 8.

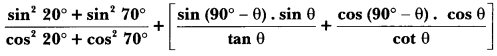
Solution:

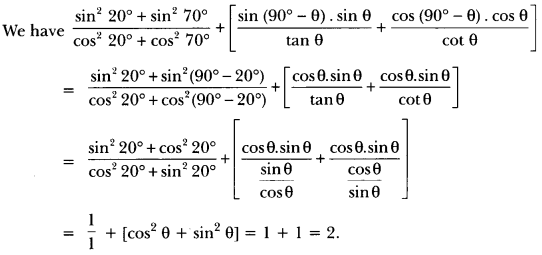
Trigonometry Problems For Class 10 Question 9.
Evaluate: sin 25° cos 65° + cos 25° sin 65°.
Solution:
sin 25°. cos 65° + cos 25° . sin 65°
= sin (90° – 65°). cos 65° + cos (90° – 65°). sin 65°
= cos 65° . cos 65° + sin 65°. sin 65°
= cos² 65° + sin² 65° = 1.

Class 10 Introduction To Trigonometry Extra Questions Question 10.
Without using tables, evaluate the following:
3 cos 68°. cosec 22° – \(\frac{1}{2}\) tan 43°. tan 47°. tan 12°. tan 60°. tan 78°
Solution:
We have,
3 cos 68°. cosec 22° – \(\frac{1}{2}\) tan 43°. tan 47°. tan 12°. tan 60°. tan 78°.
= 3 cos (90° – 22°). cosec 22° – \(\frac{1}{2}\) . {tan 43° . tan (90° – 43°)}. {tan 12°. tan (90° – 12°). tan 60°}
= 3 sin 22°. cosec 22° – \(\frac{1}{2}\)(tan 43° . cot 43°). (tan 12°. cot 12°). tan 60°
= 3 × 1 – × 1 × 1 × √3 = 3 – \(\frac{\sqrt{3}}{2}\) = \(\frac{6-\sqrt{3}}{2}\).

Question 11.
If sin 30 = cos (θ – 6°) where 30 and (θ – 6°) are both acute angles, find the value of θ.
Solution:
According to question:
sin 3θ = cos (θ – 6°)
cos (90° – 30) = cos (θ – 6°) [∵ cos (90° – θ ) = sin θ]
90° – 3θ = θ – 6° [comparing the angles)
= 4θ = 90° + 6° = 96°
θ = \(\frac{96}{4}\) = 24°
Hence, θ = 24°

Question 12.
If sec θ = x + \(\frac{1}{4x}\), prove that sec θ + tan θ = 2x or \(\frac{1}{2x}\).
Solution:
Let sec θ + tan θ = λ …..(i)
We know that, sec² θ – tan² θ = 1
(sec θ + tan θ) (sec θ – tan θ) = 1
⇒ λ(sec θ – tan θ) = 1
sec θ – tan θ = \(\frac{1}{\lambda}\) …..(ii)
Adding equations (i) and (ii), we get

Question 13.
Find an acute angle θ, when

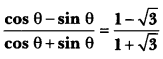
Solution:

On comparing we get
⇒ tan θ = √3
⇒ tan θ = tan 60°
= θ = 60°

Question 14.
The altitude AD of a MABC, in which ∠A is an obtuse angle has length 10 cm. If BD = 10 cm and CD = 10√3 cm, determine ∠A.
Solution:

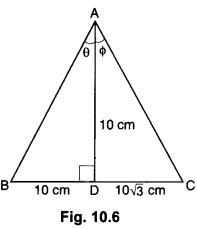
∆ABD is a right triangle right angled at D, such that AD = 10 cm and BD = 10 cm.
Let ∠BAD = θ
∴ tan θ = \(\frac{B D}{A D}\)
⇒ tan θ = \(\frac{10}{10}\) = 1
⇒ tan θ = tan 45°
⇒ θ = ∠BAD = 45° … (i)
∆ACD is a right triangle right angled at D such that AD = 10 cm and DC = 10√3 cm.
Let ∠CAD = Φ
∴ tan Φ = \(\frac{CD}{AD}\)
⇒ tan Φ = \(\frac{10 \sqrt{3}}{10}\) = √3
⇒ tan Φ = tan 60°
⇒ Φ = ∠CAD = 60°
From (i) & (ii), we have
∠BAC = ∠BAD + ∠CAD = 45° + 60° = 105°

Question 15.
If cosec θ = \(\frac{13}{12}\), evaluate \(\frac{2 \sin \theta-3 \cos \theta}{4 \sin \theta-9 \cos \theta}\)
Solution:

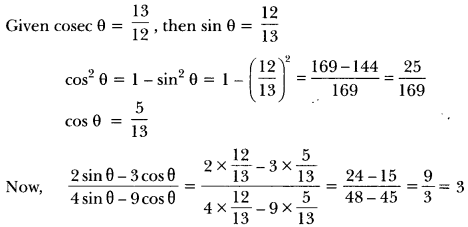
Question 16.
Prove that

Solution:

Question 17.
Prove that

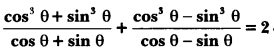
Solution:
We have,

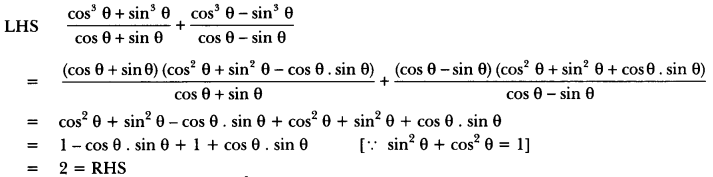
Question 18.
Prove that:

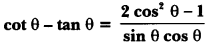
Solution:

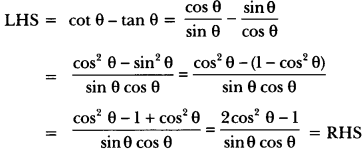
Question 19.
Prove that:

Solution:

Question 20.
Evaluate the following:

Solution:

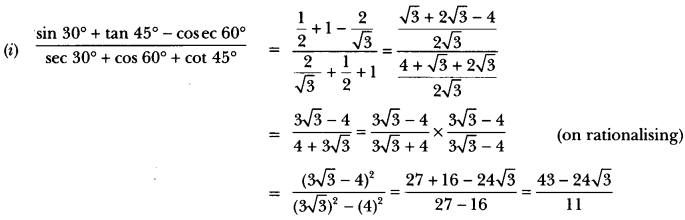
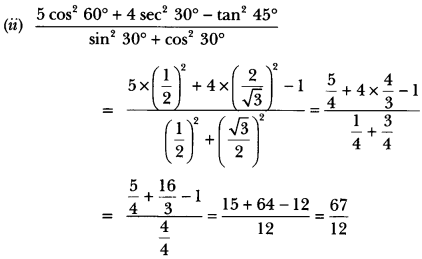
Question 21.
If tan (A +B) = √3 and tan (A – B) = \(\frac{1}{\sqrt{3}}\); 0° < A + B ≤ 90°; A > B, find A and B.
Solution:
We have, tan (A + B) = √3
⇒ tan (A + B) = tan 60°
∴ A + B = 60° …(i)
Again, tan (A – B) = \(\frac{1}{\sqrt{3}}\)
∴ A – B = 30° … (ii)
Adding (i) and (ii), we have
2A = 90°
⇒ A = 45°
Putting the value of A in (i), we have
45° + B = 60°
∴ B = 60° – 45o = 15°
Hence, A = 45° and B = 15°

Question 22.
If A, B and C are interior angles of a ∆ABC, then show that sin \(\left(\frac{B+C}{2}\right)\) = cos\(\frac{A}{2}\).
Solution:
Since A, B and C are the interior angles of a ∆ABC,

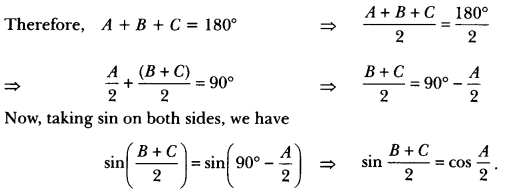
Question 23.
Prove that: (cosec θ – cot θ)² = \(\frac {1-\cos\theta}{1+\cos\theta}\)
Solution:
LHS = (cosec θ – cot θ)²

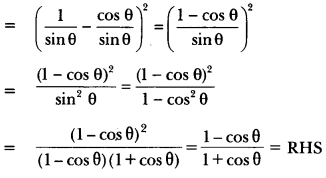
Question 24.
Prove that:

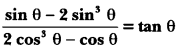
Solution:

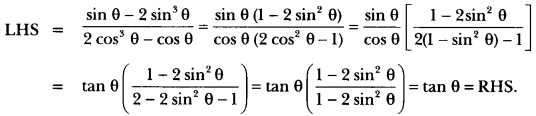
Question 25.
Prove that: (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot²A.
Solution:
LHS = (sin A + cosec A)² + (cos A + sec A)²
= sin² A + coses² A + 2sin A . cosec A + cos² A + sec² A + 2 cos A . sec A
= (sin² A + coses² A + 2) + (cos² A + sec² A + 2) [sin A. cosec A = 1]
= (sin² A + cos² A) + (coses² A + sec² A) + 4 [cos A. sec A = 1]
= 1 + 1 + cot²A + 1 + tan² A + 4
= 7 + tan² A + cot² A = RHS [∵ 1 + cot²A = coses² A and 1 + tan² A = sec² A]

Question 26.
Prove that:

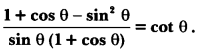
Solution:

To obtain cot θ in RHS, we have to convert the numerator of LHS in cosine function and denominator in sine function.
Therefore converting sin² θ = 1 – cos² θ, we get

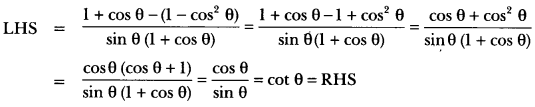
Question 27.
Prove that:

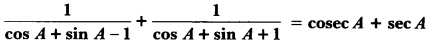
Solution:

Question 28.
Prove that:

Solution:

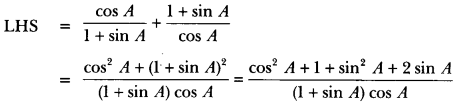
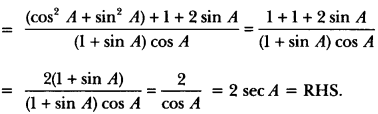
Question 29.
Without using trigonometric tables, prove that:

Solution:

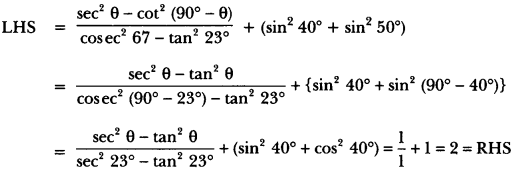
Question 30.
Evaluate:

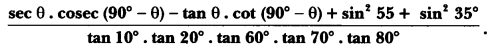
Solution:

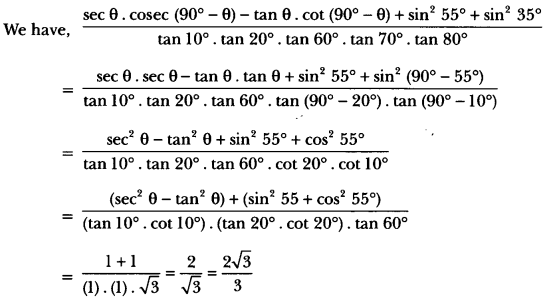
Introduction to Trigonometry Class 10 Extra Questions Long Answer Type

Question 1.
In ∆PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:

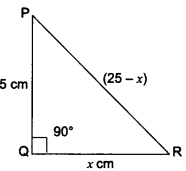
We have a right-angled ∆PQR in which ∠Q = 90°.
Let QR = x cm
Therefore, PR = (25 – x) cm
By Pythagoras Theorem, we have
PR² = PQ² + QR²
(25 – x)² = 5² + x²
= (25 – x)² – x² = 25
(25 – x – x) (25 – x + x) = 25
(25 – 2x) 25 = 25
25 – 2x = 1
25 – 1 = 2x
= 24 = 2x
∴ x = 12 cm
Hence, QR = 12 cm
PR = (25 – x) cm = 25 – 12 = 13 cm
PQ = 5 cm

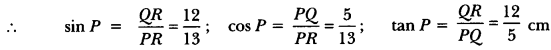
Question 2.
In triangle ABC right-angled at B, if tan A = \(\frac{1}{\sqrt{3}}\) find the value of:
(i) sin A cos C + cos A sin C (ii) cos A cos C – sin A sin C.
Solution:

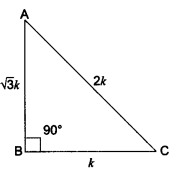
We have a right-angled ∆ABC in which ∠B = 90°.
and, tan A = \(\frac{1}{\sqrt{3}}\)
Now, tan A = \(\frac{1}{\sqrt{3}}\) = \(\frac{BC}{AB}\)
Let BC = k and AB = √3k
∴ By Pythagoras Theorem, we have
⇒ AC² = AB² + BC²
⇒ AC² = (√3k)² + (k)² = 3k² + k²
⇒ AC² = 4k²

Question 3.
If cot θ = \(\frac{7}{8}\), evaluate:
(i)

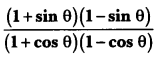
(ii) cot² θ
Solution:
Let us draw a right triangle ABC in which ∠B = 90° and ∠C = θ.

Question 4.
If 3 cot A = 4, check whether \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos² A – sin² A or not.
Solution:

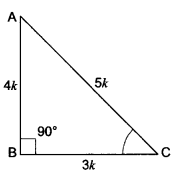
Let us consider a right triangle ABC in which ∠B = 90°

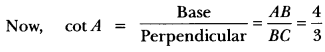
Let AB = 4k and BC = 3k
∴ By Pythagoras Theorem
AC² = AB² + BC²
AC = (4k)² + (3k)² = 16k² + 9k²
AC² = 25k²
∴ AC = 5k

Question 5.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:

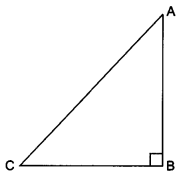
Let us consider a right-angled ∆ABC in which ∠B = 90°.
For ∠A we have

Question 6.
Prove that

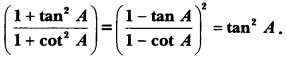
Solution:

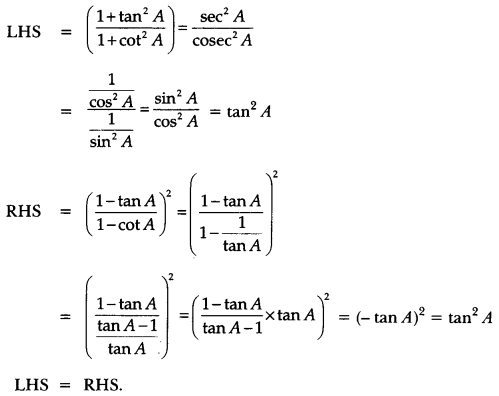
Question 7.
Prove that:

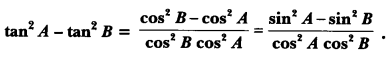
Solution:

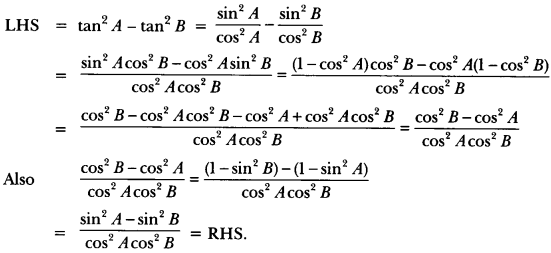
Question 8.
Prove that

Solution:

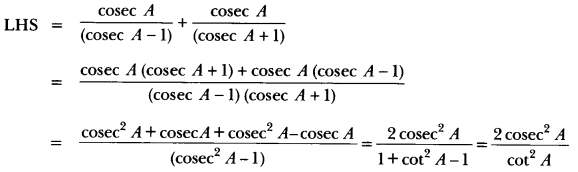
= 2 cosec² A tan² A = 2(1 + cot² A). tan² A
= 2 tan² A + 2 tan² A. cot² A (∵ tan A cot A = 1)
= 2 + 2 tan² A = 2(1 + tan² A) = 2 sec² A = RHS.

Question 9.
Prove that: (sin θ + sec θ)² + (cos θ + cosec θ)² = (1 + sec θ cosec θ)².
Solution:
LHS = (sin θ + sec θ)2 + (cos θ + cosec θ)²

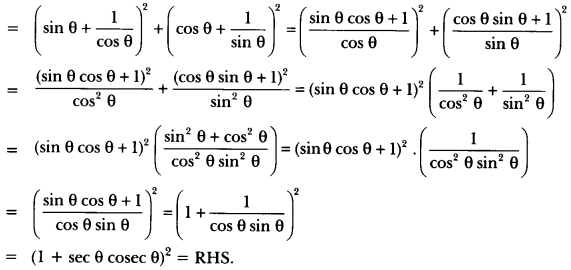
= (1 + sec θ cosec θ)² = RHS.

Question 10.
Prove that:

Solution:
In order to show that,

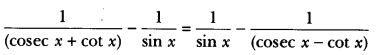
Question 11.
Prove that: \(\frac { cosecθ\quad +\quad cotθ }{ cosecθ\quad -\quad cotθ } \) = (cosec θ + cot θ) = 1 + 2 cot² θ + 2 cosec θ cot θ.
Solution:

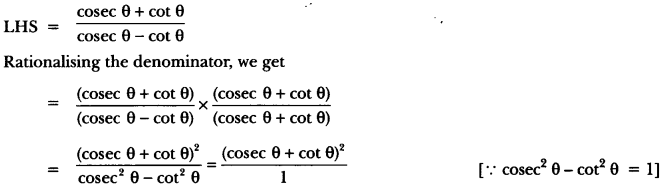
= cosec² θ + cot² θ + 2 cosec θ. cot θ
= (1 + cot² θ) + cot² θ + 2 cosec θ. cot θ
= 1 + 2 cot² θ + 2 cosec . cot θ = RHS.

Question 12.
Prove that: 2 sec θ – sec θ – 2 cosec θ + cosec θ = cot – tan θ.
Solution:
LHS = 2 sec θ – sec θ – 2 cosec² θ + cosec θ
= 2 (sec² θ) – (sec² θ)2 – 2 (cosec² θ) + (cosec θ)²
= 2 (1 + tan² θ) – (1 + tan⁴ θ)2 – 2(1 + cot² θ) + (1 + cot² θ)⁴
= 2 + 2 tan² θ – (1 + 2 tan² θ + tan² θ) – 2 – 2 cot² θ + (1 + 2 cot² θ + cot θ) =
= 2 + 2 tan² θ – 1 – 2 tan² θ – tan⁴ θ – 2 – 2 cot² θ + 1 + 2 cot⁴ θ + cot⁴ θ
= cot⁴ θ – tan⁴ θ = RHS

Question 13.
Prove that: (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\).
Solution:
LHS = (cosec A – sin A) (sec A – cos A)

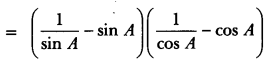
Introduction to Trigonometry Class 10 Extra Questions HOTS

Question 1.
Prove that:
\(\frac{\tan \theta}{1-\cot \theta}\) + \(\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ = 1 + tan θ + cot θ.
Solution:

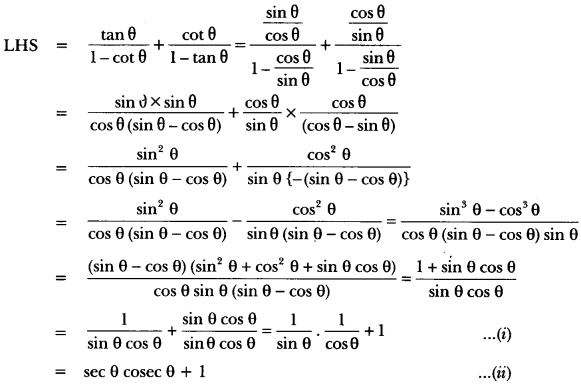
For second part
Now from (i), we have

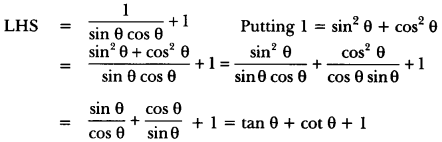
Question 2.
If tan A = n tan B and sin A = m sin B, prove that cos² A = \(\frac{m^{2}-1}{n^{2}-1}\)
Solution:
We have to find cos² A in terms of m and n. This means that the angle B is to be eliminated from
the given relations.
Now, tan A = n tan B
⇒ tan B = \(\frac{1}{n}\) tan A
⇒ cot B = \(\frac{n}{\tan A}\)
and
sin A = m sin B

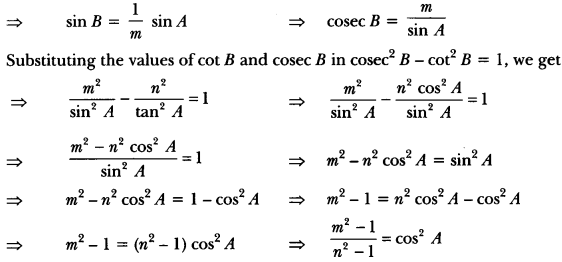
Question 3.
Prove the following identity, where the angle involved is acute angle for which the expressions are defined.
\(\frac { cosA-sinA+1 }{ cos A + sin A-1 } \) = cosec A + cot A, using the identity cosec² A = 1 + cot² A.
Solution:

= cosec A + cot A = RHS.

Question 4.
If x sin³ + y cos³ θ = sin θ cos θ and x sin θ = y cos θ, prove x² + y² = 1.
Solution:
We have, x sin³ + y cos³ θ = sin θ cos θ
⇒(x sin θ) sin² θ + (y cos θ) cos² θ sin θ cos θ
⇒ x sin θ (sin² θ) + (x sin θ) cos² = sin θ cos [∵ x sin θ = y cos θ]
⇒ x sin θ (sin² θ + cos² θ) = sin θ cos θ
⇒ x sin θ = sin θ cos
⇒ x = cos θ
Now, we have x sin θ = y cos θ
⇒ cos o sin θ = y cos θ [∵ x = cos θ]
⇒ y = sin θ
Hence, x² + y² = cos² θ + sin² θ = 1.

Question 5.
If tan θ + sin θ = m and tan θ – sin θ = n, show that (m² – n²) = 4√mn.
Solution:
We have, given tan θ + sin θ = m, and tan θ – sin θ = n, then
LHS = (m² – n²),= (tan θ + sin θ)² – (tan θ – sin )²
= tan² θ + sin² θ + 2 tan θ sin θ – tan² θ – sin² θ + 2 tan θ sin θ

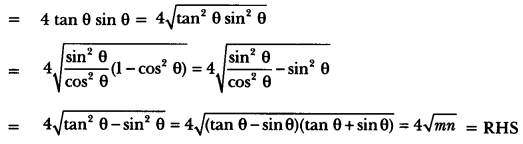
Question 6.
If cosec θ – sin θ = l and sec θ – cos θ = m, prove that l² m² (l² + m² + 3) = 1.
Solution:
LHS = l² m² (l² + m² + 3).
= (cosec θ – sin θ)² (sec θ – cos θ)² {(cosec θ – sin θ)² + (sec θ – cos θ)² + 3}