By going through these CBSE Class 12 Maths Notes Chapter 2 Inverse Trigonometric Functions, students can recall all the concepts quickly.
Inverse Trigonometric Functions Notes Class 12 Maths Chapter 2
Inverse Function Calculator is an online tool by Protonstalk to quickly and easily find out the inverse of any given function.
As we have learned in class XI, the domain and range of trigonometric functions are given below:
Functions Domain Range

→ Inverse Function: We know that if f: X →Y such that y = f(x) is one-one and onto, then we define another function g : Y → X such that x = g(y), where x ∈ X and y ∈ Y, which is also one-one and onto.
In such a case, Domain of g = Range of f and Range of g = Domain of f.
g is called the inverse of f or g = f-1.
∴ Inverse of g = g-1 = (f-1)-1 =f.
The graph of the sin-1 function is shown here.
Principal Value Branch of Function sin-1:
It may be noted that for the domain [-1,1}, the range could be any one of the intervals. …..,
[\(\frac{-3 \pi}{2}\), \(\frac{-\pi}{2}\)], [\(\frac{-\pi}{2}\), \(\frac{\pi}{2}\)] or [\(\frac{\pi}{2}\), \(\frac{3\pi}{2}\)] …….
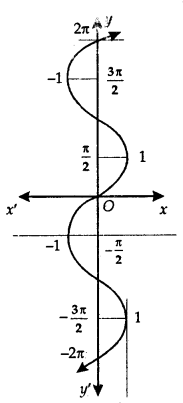
Corresponding to each interval, we get a branch of the function sin-1.
The branch with range [\(\frac{-\pi}{2}\), \(\frac{\pi}{2}\)] is called the principal value branch.
Thus, sin-1: [-1,1] → [\(\frac{-\pi}{2}\), \(\frac{\pi}{2}\)]
Principal Value Branch of Function cos-1:
The graph of the function cos-1 is as shown here.
The domain of the function cos-1 is [-1,1]. Its range is one of the intervals. ………., (-π, 0), (0, π), (π, 2π), ………… It is one-one and onto with the range [-1, 1]. The branch with range (0, π) is called the principal value branch of the function cos-1. Thus, cos-1: [-1,1] → [0, π].
Principal Value Branch of Function tan-1:
The function tan-1 is defined whose domain is set of real numbers and range is one of the intervais. [ \(\frac{-3 \pi}{2}\), \(\frac{-\pi}{2}\)], [\(\frac{-\pi}{2}\), \(\frac{\pi}{2}\)] or [\(\frac{\pi}{2}\), \(\frac{3 \pi}{2}\)]…………
The graph of the function is as shown in the adjoining figure.
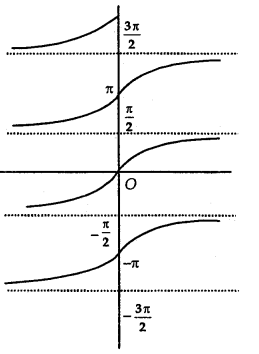
The branch with range [\(\frac{-\pi}{2}\), \(\frac{\pi}{2}\)] is called the principal value branch of function tan1. Thus, tan-1: R → [\(\frac{-\pi}{2}\), \(\frac{\pi}{2}\)].
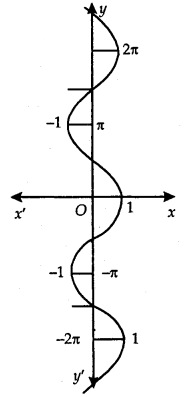
Principal Value Branch of Function cosec-1:
The graph of function cosec-1 is as shown here. The function cosec-1 defined whose domain is R — (-1, 1) and the range is any one of the intervals …….., [ \(\frac{-3 \pi}{2}\), \(\frac{-\pi}{2}\)] – {π}, [\(\frac{-\pi}{2}\), \(\frac{\pi}{2}\)] – {0}, [\(\frac{\pi}{2}\), \(\frac{3 \pi}{2}\)] – {π}……..
The function corresponding to the range [\(\frac{-\pi}{2}\), \(\frac{\pi}{2}\)] – {0} is called the principal value branch of cosec-1.
Thus, cosec-1: R – (-1, 1) → [\(\frac{-\pi}{2}\), \(\frac{\pi}{2}\)] – {0}.
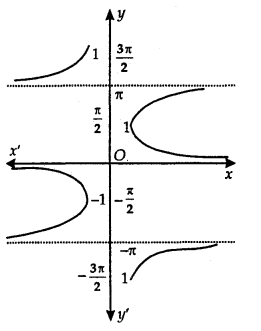
Principal Value Branch of Function sec-1:
The graph of function sec-1 is shown in adjoining figure. The sec-1 is defined as a function whose domain is R – (-1, 1) and the range is one of the intervals……. [- π, 0] – {\(\frac{-\pi}{2}\)}, [0, π] – {\(\frac{\pi}{2}\)}, [π, 2π] – {\(\frac{3 \pi}{2}\)}, ……………
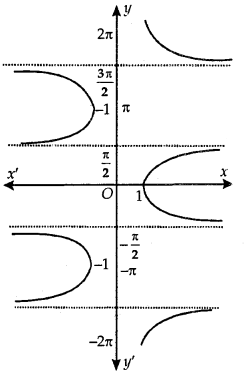
The function corresponding to [0, π] – {\(\frac{\pi}{2}\)} is known as the range [0, π] – {\(\frac{\pi}{2}\)} is known as the principal value branch of sec-1.
Thus, sec-1: R – (-1,1) → [0, π] – {\(\frac{\pi}{2}\)}
Principal Value Branch of Function cot-1:
The graph of function cor’ is as shown here.
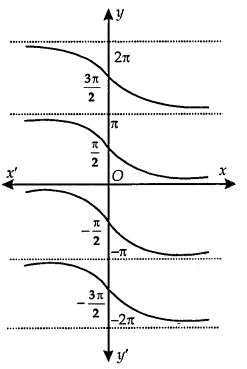
The cot-1 function is defined as a function whose domain is R and the range is any of the intervals, …………
(-π, 0), (0, π), (π, 2π), …………
The function corresponding to (0, π) is called the principal value branch of the function cot-1.
Thus, cot-1: R → (0, π).
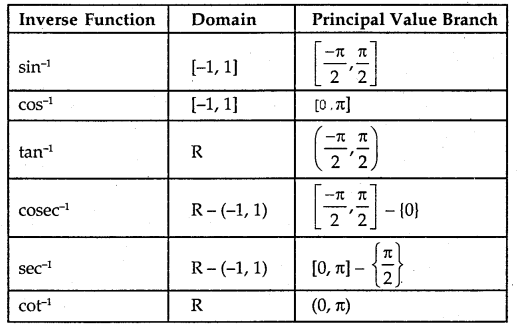
The principal value branch of trigonometric inverse functions are as follows:
→ Some Important Results:
1. (a) sin-1\(\frac{1}{x}\) = cosec-1x, x ≥ 1, x ≤ -1
(b) cos-1 \(\frac{1}{x}\) = sec-1x, x ≥ l, x ≤ -1
(c) tan-1 \(\frac{1}{x}\) = cot-1x, x > 0
(d) cosec-1 \(\frac{1}{x}\) = sin-1x, x ∈ [-1,1]
(e) sec-1 \(\frac{1}{x}\) = cos-1x, x ∈ [-1,1]
(f) cot-1 \(\frac{1}{x}\) = tan-1x, x > 0.
2. (a) sin-1(-x) = – sin-1x, x ∈ [-1,1]
(b) tan-1(-x) = – tan-1x, x ∈ R
(c) cosec-1(-x) = – cosec-1x, | x | >1
(d) cos-1(-x) = π – cos-1x, x ∈ [-1,1]
(e) sec-1(-x) = π – sec-1x, x ∈ R
(f) cot-1(-x) = π – cot-1x, x ∈ R
3. (a) sin-1x + cos-1x = \(\frac{x}{2}\), x ∈ [-1,1]
(b tan-1x + cot-1x = \(\frac{x}{2}\), x ∈ R
(c) cosec-1x + sec-1x = \(\frac{x}{2}\), | x | ≥ 1
4. (a) tan-1x + tan-1y = tan-1\(\frac{x+y}{1-x y}\), xy < 1
(b) tan-1x – tan-1y = tan-1\(\frac{x-y}{1+x y}\), xy > -1
(c) 2 tan-1x = tan-1\(\frac{2 x}{1-x^{2}}\), | x | <1
= sin-1\(\frac{2 x}{1+x^{2}}\), | x | <0
= cos-1\(\frac{1-x^{2}}{1+x^{2}}\) , x ≥ 0
(d) 2sin-1x = sin-1[2x\(\sqrt{1-x^{2}}\)]
(e) 2cos-1x = cos-1(2x2 – 1)
1. Table
| Function | Principal Value Branch | |
| Domain | Range | |
| (i) y = sin-1 x | – 1 ≤ x ≤ 1 | \(-\frac{\pi}{2}\) ≤ y ≤ \(\frac{\pi}{2}\) |
| (ii) y = cos-1 x | – 1 ≤ x ≤ 1 | 0 ≤ y ≤ π |
| (iii) y = tan-1x | – ∞ < x < ∞ | \(-\frac{\pi}{2}\) < y < \(\frac{\pi}{2}\) |
| (iv) y = cot-1 x | – ∞ < x ≤ -1 | 0 < y < \(\frac{\pi}{2}\) |
| (v) y = sec-1 x | 1 ≤ x < ∞ -∞ < x ≤ -1 |
0 ≤ y < \(\frac{\pi}{2}\) \(\frac{\pi}{2}\)< y < π |
| (vi) y = cosec-1 x | 1 ≤ x < ∞ -∞ < x ≤ ∞ |
0 < y ≤ \(\frac{\pi}{2}\) \(-\frac{\pi}{2}\) ≤ y < 0 |
2. PROPERTIES :
(i) x = sin-1(sin x) = cos-1(cos x) = tan-1 (tan x); etc.
(ii) (a) cosec-1x = sin-1 \(\frac { 1 }{ x }\) , x ≥ 1 or x ≤ -1
(b) sec-1 x = cos-1\(\frac { 1 }{ x }\) ,x ≥ 1 or x ≤ -1
(c) cot-1x = tan-1\(\frac { 1 }{ x }\), x > 0.
(iii) (a) sin-1 (- x) = – sin-1x, x ∈ [-1,11
(b) cos-1 (-x) = π – cos-1x, x ∈ [- 1, 1]
(c) tan-1(- x) = – tan-1 x, x ∈ R
(d) cot-1(-x) = π – cot-1 x, x ∈ R
(e) sec-1 (-x) = π – sec-1 x, |x| ≥ 1
(f) cosec-1 (- x) = – cosec-1 x, |x| ≥ 1
(iv) (a) sin-1 x + cos-1 x = \(\frac{\pi}{2}\), x ∈ (-1,1)
(b) tan -1 x + cot-1x = \(\frac{\pi}{2}\) x ∈ R
(c) sec-1x + cosec-1= \(\frac{\pi}{2}\), |x| ≥ 1
(d) tan-1 x + tan-1 = tan-1 \(\frac{x+y}{1-x y}\), xy > -1
(e) tan-1x – tan-1y = tan-1 \(\frac{x-y}{1+x y}\), xy > -1
(f) 2tan-1 x = sin-1 \(\frac{2 x}{1+x^{2}}\) = cos-1 \(\frac{2 x}{1-x^{2}}\) = tan-1
(v) (a) sin -1x ± sin-1 y = sin -1 \(\left(x \sqrt{1-y^{2}} \pm y \sqrt{1-x^{2}}\right)\)
(b) cos -1x ± cos-1y = cos -1 \(\left(x y \mp \sqrt{1-x^{2}} \sqrt{1-y^{2}}\right)\)