Here we are providing Linear Equations for Two Variables Class 9 Extra Questions Maths Chapter 4 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-9-maths/
Extra Questions for Class 9 Maths Linear Equations for Two Variables with Answers Solutions
Extra Questions for Class 9 Maths Chapter 4 Linear Equations for Two Variables with Solutions Answers
Linear Equations for Two Variables Class 9 Extra Questions Very Short Answer Type
Linear Equations In Two Variables Class 9 Extra Questions Question 1.
Linear equation x – 2 = 0 is parallel to which axis ?
Solution:
Here, linear equation is x – 2 ⇒ 0 x = 2
Thus, it is parallel to the y-axis.
Linear Equations Class 9 Extra Questions Question 2.
Express x in term of y: \(\frac{x}{7}\) + 2y = 6
Solution:
Given equation is
\(\frac{x}{7}\) + 2y = 6
⇒ \(\frac{x}{7}\) = 6 – 2y
Thus, x = 7(6 – 2y).
Linear Equations In Two Variables Extra Questions Class 9 Question 3.
If we multiply or divide both sides of a linear equation with a non-zero number, then what will happen to the solution of the linear equation ?
Solution:
Solution remains the same.
Class 9 Maths Chapter 4 Extra Questions Question 4.
Find the value of k for which x = 0, y = 8 is a solution of 3x – 6y = k.
Solution:
Since x = 0 and y = 8 is a solution of given equation
3x – 6y = k
3(0) – 6(8) = k
⇒ k = – 48
Class 9 Linear Equations In Two Variables Extra Questions Question 5.
Write the equation of a line which is parallel to x-axis and is at a distance of 2 units from the origin.
Solution:
Here, required line is parallel to x-axis and at a distance of 2 units from the origin.
∴ Its equation is
y + 2 = 0
or y – 2 = 0
Extra Questions For Class 9 Maths Chapter 4 With Solution Question 6.
Find ‘a’, if linear equation 3x – ay = 6 has one solution as (4, 3).
Solution:
Since (4, 3) is a solution of given equation.
∴ 3(4) – a(3) = 6
⇒ 12 – 3a = 6
⇒ a = \(\frac{-6}{-3}\)
Hence, a = 2
Linear Equations In Two Variables Class 9 Extra Questions With Solutions Question 7.
Cost of a pen is two and half times the cost of a pencil. Express this situation as a linear equation in two variables.
Solution:
Let cost of a pen be ₹ x and cost of a pencil be ₹ y.
According to statement of the question, we have
x = 2\(\frac{1}{2}\) y
⇒ 2x = 5y or 2x – 5y = 0
Extra Questions On Linear Equations In Two Variables Class 9 Question 8.
In an one day international cricket match, Raina and Dhoni together scored 198 runs. Express the statement as a linear equation in two variables.
Solution:
Let runs scored by Raina be x and runs scored by Dhoni be y.
According to statement of the question, we have
x + y = 198
x + y – 198 = 0
Extra Questions For Class 9 Maths Linear Equations In Two Variables Question 9.
The cost of a table is 100 more than half the cost of a chair. Write this statement as a linear equation in two variables.
Solution:
Let the cost price of a table be ₹ x and that of a chair be ₹ y.
Since the cost price of a table is 100 more than half the cost price of a chair.
∴x = \(\frac{1}{2}\)y + 100
⇒ 2x = y + 200 or 2x – y – 200 = 0.
Linear Equations for Two Variables Class 9 Extra Questions Short Answer Type 1
Class 9 Maths Ch 4 Extra Questions Question 1.
Write linear equation representing a line which is parallel to y-axis and is at a distance of 2 units on the left side of y-axis.
Solution:
Here, required equation is parallel to y-axis at a distance of 2 units on the left side of y-axis.
x = -2 or x + 2 = 0
Chapter 4 Maths Class 9 Extra Questions Question 2.
In some countries temperature is measured in Fahrenheit, whereas in countries like India it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius :
F = \(\left(\frac{9}{5}\right)\)C + 32°
If the temperature is – 40°C, then what is the temperature in Fahrenheit?
Solution:
Given linear equation is
F = \(\left(\frac{9}{5}\right)\)C + 32°
Put C = -40°, we have
F = \(\frac{9}{5}\)(-40°) + 32°
F = – 72° + 32°
F= -40°
Ch 4 Maths Class 9 Extra Questions Question 3.
Give equation of two lines on same plane which are intersecting at the point (2, 3).
Solution:
Since there are infinite lines passing through the point (2, 3).
Let, first equation is x + y = 5 and second equation is 2x + 3y = 13.
Clearly, the lines represented by both equations intersect at the point (2, 3).
Class 9 Maths Linear Equations In Two Variables Extra Questions Question 4.
If ax + 3y = 25, write y in terms of x and also, find the two solutions of this equation.
Solution:
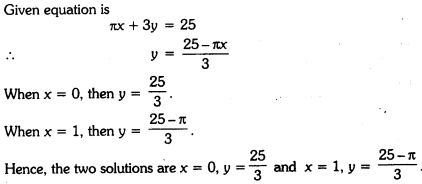
Linear Equations In 2 Variables Class 9 Extra Questions Question 5.
Find the value of k, if (1, -1) is a solution of the equation 3x – ky = 8. Also, find the coordinates of another point lying on its graph.
Solution:
Since (1, -1) is a solution of the equation 3x – ky = 8
∴ 3(1) – k(-1) = 8
⇒ k = 8 – 3 = 5
Thus, the given equation is
3x – 5y = 8
![]()
Hence, the coordinates of another point lying on the graph of 3x – 5y = 8 is (6, 2).
Linear Equations In Two Variables Class 9 Important Questions Question 6.
Let y varies directly as x. If y = 12 when x = 4, then write a linear equation. What is the value of y, when x = 5 ?
Solution:
Given y varies directly as x implies y = kx
But y = 12 for x = 4
⇒ 4k = 12 = k = 3
Put k = 3 in y = kx, we have
y = 3x
Now, when x = 5, y = 3 x 5 = y = 15 …(i)
Linear Equations for Two Variables Class 9 Extra Questions Short Answer Type 2
Linear Equations In Two Variables Class 9 Extra Questions Pdf Question 1.
A fraction becomes , when 2 is subtracted from the numerator and 3 is added to the denominator. Represent this situation as a linear equation in two variables. Also, find two solutions for this.
Solution:
Let numerator and denominator of the given fraction be respectively x and y. According to the statement, we obtain
\(\frac{x-2}{y+3}\) = \(\frac{1}{4}\)
⇒ 4x – 8 = y + 3
⇒ 4x – y – 11 = 0
Which is the required linear equation. When y = 1, then x = 3. When y = 5, then x = 4. Hence, the two solutions are (3, 1) and (4, 5).
Extra Questions For Class 9 Maths Chapter 4 Question 2.
The path of an aeroplane is given by the equation 3x – 4y = 1 2: Represent the path graphically. Also, show that the point (-4,-6) lies on the graph.
Solution:
Given equation is 3x – 4y = 12
∴ y = \(\frac{3 x-12}{4}\).
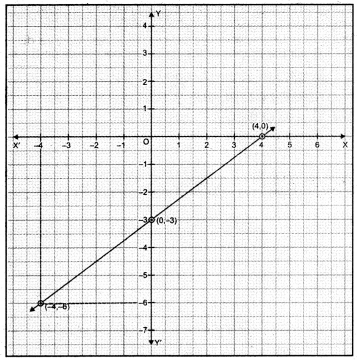
When x = 0, then y = -3
When x = 4, then y = 0
Table of solutions is
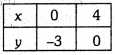
Plot the points (0, – 3), (4, 0) on the graph and join them to get the required graph. From the graph, we see, when
x = -4, then y = -6.
Therefore, (-4,- 6) lies on the graph of given equation.
Class 9 Chapter 4 Maths Extra Questions Question 3.
Express y in terms of x for the equation 3x – 4y + 7 = 0. Check whether the points (23, 4) and \(\left(0, \frac{7}{4}\right)\) lie on the graph of this equation or not.
Solution:
Given equation is 3x – 4y + 7 = 0
∴y = \(\frac{3 x+7}{4}\)
When x = -1, then y = 1
When x = 3, then y = 4
When x = 7, then y = 7
Table of solutions is :
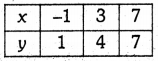
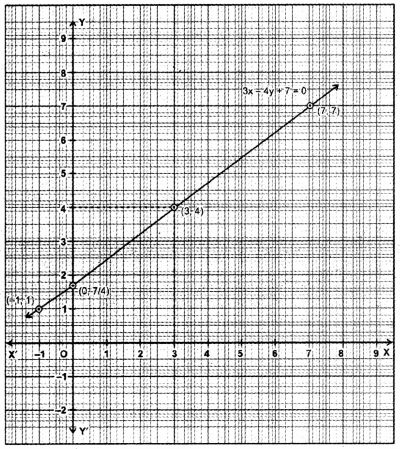
Plot the points (-1, 1), (3, 4), (7, 7). and join them to get the given graph. From the graph, we see that, when x = 0, then y \(\frac{7}{4}\) = 5 and when y = 4,
then x = 3. Thus, (0, \(\frac{7}{4}\)) lies on the graph, whereas (23, 4) does not lie on the graph.
Extra Questions Of Chapter 4 Class 9 Maths Question 4.
The following observed values of x and y are thought to satisfy a linear equation. Write the linear equation :
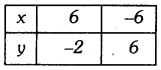
Draw the graph using the values of x, y as given in the above table. At what points the graph of the linear equation :
(i) cuts the x-axis (ii) cuts the y-axis
Solution:
Let ax + by + c = 0 ……(i)
be the linear equation in two variables. From the table, we have two points A(6, -2) and B(-6, 6) which lie on the graph of the linear equation
⇒ 6a – 2b + c = 0
and -6a + 6b + c = 0
Adding the above two equations, we obtain
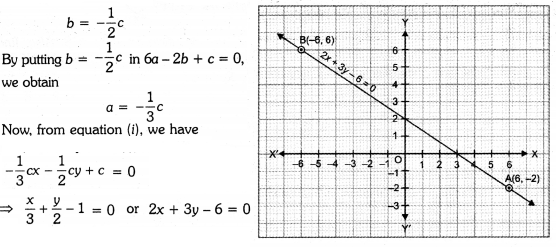
Which is the required linear equation in two variables. Plots the points A(6, -2) and B(-6, 6) on the graph. Join them to get line AB.
From the graph, we see that the graph cuts the x-axis at (3, 0) and the y-axis at (0, 2).
Linear Equations for Two Variables Class 9 Extra Questions Long Answer Type
Question 1.
Write the equations of the lines drawn in following graph :
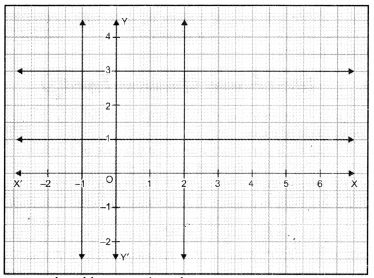
Also, find the area enclosed between these lines.
Solution:
Equations of the lines drawn in the graph are as :
x = -1 or x + 1 = 0,
x = 2 or x – 2 = 0,
y = 1 or y – 1 = 0 and
y = 3 or y – 3 = 0
Figure formed by these lines is a rectangle of dimensions 3 units by 2 units.
Hence, the area enclosed between given lines = 6 sq. units.
Question 2.
If (2, 3) and (4, 0) lie on the graph of equation ax + by = 1. Find the value of a and b. Plot the graph of equation obtained.
Solution:
(2, 3) and (4, 0) lie on the graph of equation
ax + by = 1 …(i)
∴ We have 2a + 3b = 1 … (ii)
and 4a + 0 = 1
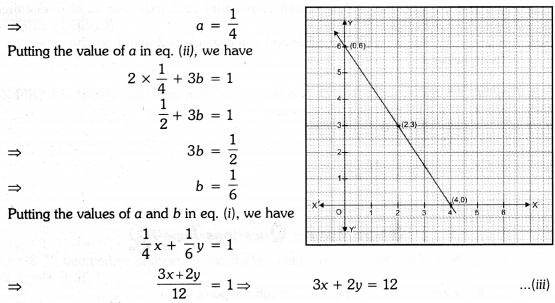
Which is required linear equation.
Put x= 0 in eq. (iii), we have
⇒ 3(0) + 2y = 12
⇒ 2y = 12
⇒ y = 6
Put x = 2 in eq. (iii), we have
⇒ 3(2) + 2y = 12
⇒ 2y = 6
⇒ y = 3
Put x = 4 in eq. (iii), we have
⇒ 3(4) + 2y = 12
⇒ 2y = 0
⇒ y = 0
We have the following table :
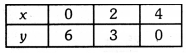
By plotting the points (0, 6), (2, 3) and (4, 0). Joining them, we obtained the graph of 3x + 2y = 12.
Question 3.
Draw the graphs of the following equations on the same graph sheet :
x = 4, x = 2, y = 1 and y – 3 = 0.
Solution:
Graphs of the given equations are drawn on graph sheet.
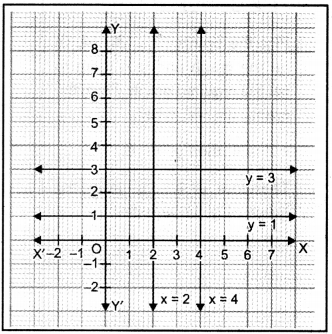
Question 4.
Cost of 1 pen is ₹ x and that of 1 pencil is ₹ y. Cost of 2 pens and 3 pencils together is ₹ 18. Write a linear equation which satisfies this data. Draw the graph for the same.
Solution:
Here, cost of 1 pen is ₹x and that
of 1 pencil is ₹ y According to the statement of the question, we have
2x + 3y = 18
⇒ x = \(\frac{18-3 y}{2}\)
When y = 0, x = 9
When y = 4, x= 3.
When y = 6, x = 0
Table of solutions is :
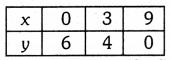
Plot the points (0, 6), (3, 4) and (9, 0). Join them in pairs to get the required line.
Question 5.
Sum of two numbers is 8. Write this in the form of a linear equation in two variables. Also, draw the line given by this equation. Find graphically the numbers, if difference between them is 2.
Solution:
Let the two numbers be x and y.
It is given that sum of two numbers is 8.
∴ x + y = 8
y = 8 – x
When x = 0,
When x = 4, y = 4
When x = 8, y = 0
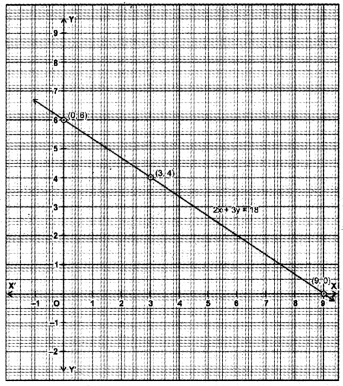
Table of solutions is :
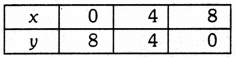
Plot the points (0, 8), (4, 4), (8, 0) and join them in pairs, we get the required graph.
When difference between two number is 2, then
x – y = 2, x > y
⇒ x = y + 2
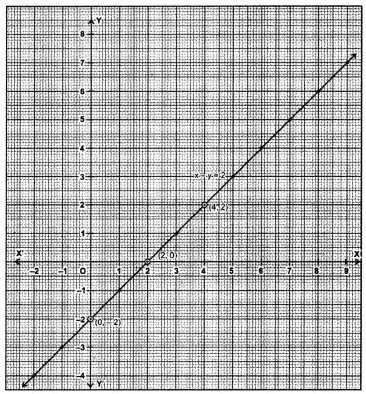
When x = 0, y = -2
When x = 2, y = 0
When x = 4, y = 2
Table of solutions is :
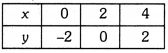
Plot these poitns (0, -2), (2, 0), (4, 2) and join them to get the required line.
Graphically, the numbers are : (-2; 4), (-1, -3), (0, -2), (1, -1), (2, 0), (3, 1), (4, 2), (5, 3), (6, 4), (7,5) etc.
Linear Equations for Two Variables Class 9 Extra Questions HOTS
Question 1.
Solve for y :
![]()
Solution:
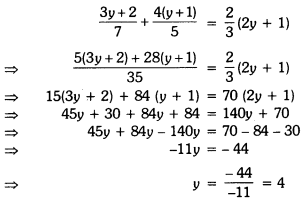
Question 2.
A and B are friends. A is elder to B by 5 years. B’s sister C is half the age of B while A’s father D is 8 years older than twice the age of B. If the present age of D is 48 years, find the present ages of A, B and C.
Solution:
Let the age of B’s sister i.e., C be x years.
∴Age of B be 2x years, age of A be (2x + 5) years.
And age of A’s father i.e., D be 2(2x) + 8 = 4x + 8 years
According to the statement of the question, we have
4x + 8 = 48
⇒ 4x = 48 – 8 = 40
⇒ x = \(\frac{40}{4}\) = 10
Age of A = (2x + 5) years i.e., (2 × 10 + 5) years = 25 years
Age of B = 2x years = 2 × 10 years = 20 years
and Age of C = \(\frac{1}{2}\) of B’s age = \(\frac{1}{2}\) × 20 years = 10 years
Linear Equations for Two Variables Class 9 Extra Questions Value Based (VBQs)
Question 1.
Mrs Sharma lost her purse containing 50 rupee and 100 rupee notes amount to 1500 in a shop. Next day shopkeeper found the purse during dusting. He immediately went to Mrs Sharma’s house and returned the purse and rupees. Mrs Sharma appreciates the shopkeeper for his act.
(i) Represent the situation as an equation and draw the graph.
(ii) What value do you learn from shopkeeper’s act ?
Solution:
(i) Let the number of 50 rupee notes be x
And the number of 100 rupee notes be y
∴ We have 50x + 100y= 1500
⇒ x + 2y = 30
(dividing each term by 50)
2y = 30 – x
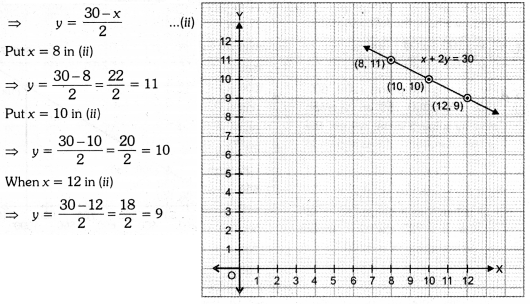
We have the following table :
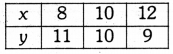
By plotting the points (8, 11), (10, 10) and (12, 9) on the graph and by joining them, we obtain the straight line represented by equation
(i) as shown in graph.
(ii) We should be always honest to feel good.
Question 2.
In an election, a good candidate may lose because 40% of voters do not cast their votes due to various reasons. Form an equation and draw the graph with data. From the graph, find :
(i) The total number of voters, if 720 voters cast their votes.
(ii) The number of votes cast, if the total number of voters are 1000.
(iii) What message did you get from above information ?
Solution:
(i) We have, total number of voters who do not cast their votes = 40%
⇒ Total number of voters who cast their votes = 60%
Let the total number of voters be x and number of voters cast their votes be y
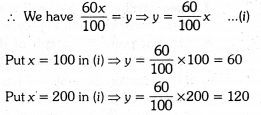
![]()
Thus, we have the following table :

By plotting the points (100, 60), (200, 120), (300, 180) on the graph and by joining them, we get the graph of equation (i) as shown in figure.
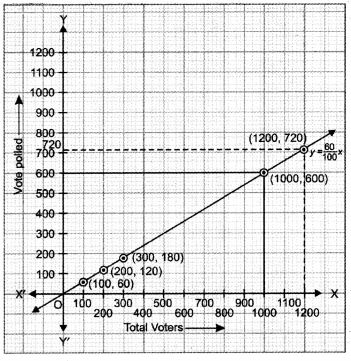
From the graph, we see that:
(i) When total votes polled = 720
i.e., y = 720, the total number of voters i.e., x = 1200
Hence, total number of voters = 1200.
(ii) When total number of voters x = 1000
Number of votes cast is 600.
(iii) Every voters should cast vote to elect an honest candidate.
