On this page, you will find Lines and Angles Class 7 Notes Maths Chapter 5 Pdf free download. CBSE NCERT Class 7 Maths Notes Chapter 5 Lines and Angles will seemingly help them to revise the important concepts in less time.
CBSE Class 7 Maths Chapter 5 Notes Lines and Angles
Lines and Angles Class 7 Notes Conceptual Facts
1. Line: A line is a perfectly straight figure extended for ever in both directions.
Example :
represent by \(\stackrel{\leftrightarrow}{A B}\)
2. Line segment: The shortest distance between any two point is called line segment. It has no end points.
Example :
represent by \(\overline{\mathrm{PQ}}\)
3. Ray: A line segment extended to one direction only is called a ray. It has one initial point and no definite length.
Example :
represent by \(\overrightarrow{\mathrm{OP}}\)
4. Angle: An angle is formed when two lines or line segments meet or intersect each other.
OR
Two rays having same initial point form an angle.
Example :
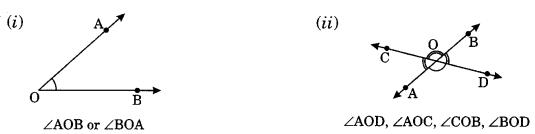
Type of angles:
(i) Acute angle: An angle whose measure is more than 0° and less than 90° is called an acute angle.
Example:
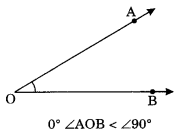
(ii) Obtuse angle: An angle whose measure is more than 90° and less than 180° is called obtuse angle.
Example:
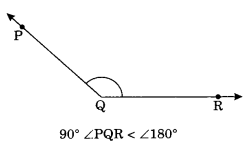
(iii) Right angle: An angle whose measure is 90° is called right angle.
Example:
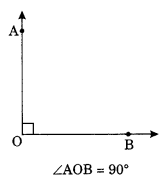
(iv) Straight angle: An angle whose measure is 180° is called straight angle.
Example:
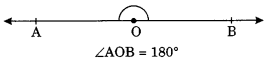
(v) Reflex angle: An angle whose measure is more than 180° but less than 360° is called reflex angle.
Example:
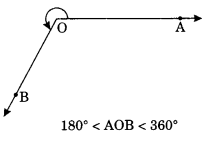
Pair of angles:
(i) Adjacent angles: Two angles having a common aim and a common vertex and non-common arms he on either side of the common arm are called adjacent angles.
Example:
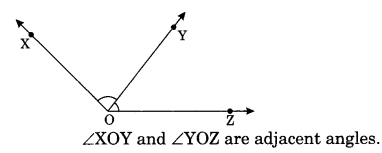
(ii) Complementary angles: Any two angles whose sum is 90° are called complementary angles.
Example:
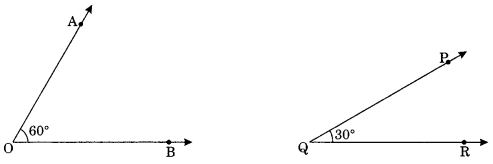
∠AOB = 60° and ∠PQR = 300
∠AOB + ∠PQR = 60° + 30° = 90°
∴ ∠AOB and ∠PQR are complementary angles.
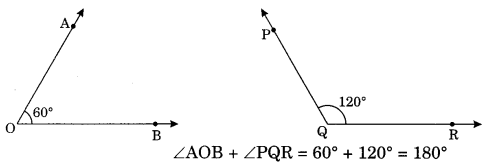
(iii) Supplementary angles: Any two angles whose sum is 180° are called supplementary angles.
∠AOB and ∠PQR are supplementary angles.
Example:
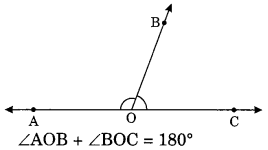
(iv) Linear pair of angles: When the sum of two adjacent angles is 180°, then they are called linear pairs.
Example:
(v) Vertically opposite angles: When two lines intersect each other, they form a pair of angles opposite to each other.
Example:
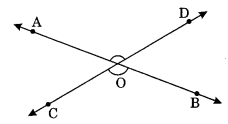
∠AOD and ∠COB) and (∠AOC and ∠BOD) are the pairs of vertically opposite angles.
Vertically opposite angles are always equal to each other, i.e., ∠AOD = ∠COB and ∠AOC = ∠BOD
Pairs of Lines:
(i) Intersecting Lines: The two lines are said to be intersecting lines if they have a common point which is known as point of intersection.
Example:
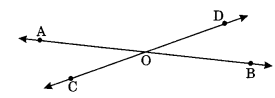
\(\stackrel{\leftrightarrow}{\mathrm{AB}} \text { and } \stackrel{\leftrightarrow}{\mathrm{CB}}\) are intersecting lines having common point O.
(ii) Parallel lines: Two lines are said to be parallel if they do not intersect each other even on extended in either direction.
Example:
\(\stackrel{\leftrightarrow}{\mathrm{PQ}} \text { and } \stackrel{\leftrightarrow}{\mathrm{AB}} \) are parallel to each other and represented as \(\stackrel{\leftrightarrow}{P Q} \| \stackrel{\leftrightarrow}{A B}\).
Transversal: When a line intersect two or more lines in a plane at distinct points it is called as transversal.
Example:
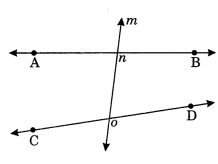
m is the transversal intersecting two line \(\stackrel{\leftrightarrow}{A B} \text { and } \stackrel{\leftrightarrow}{C D}\) at n and o respectively.
Angles made by transversal
Here \(l_{1} \| l_{2}\) and t is the transversal line.
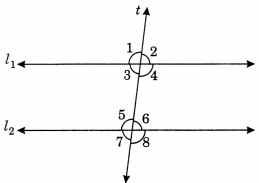
| Types of angles | Angles represented by |
| Interior | ∠3, ∠4, ∠5, ∠6 |
| Exterior | ∠1, ∠2, ∠7, ∠8 |
| Alternate interior | (∠3 and ∠6), (∠4 and ∠5) |
| Alternate exterior | (∠1 and ∠8), (Z2 and Z7) |
| Corresponding | (∠3 and ∠7), (∠1 and ∠5), (∠2 and ∠6), (∠4 and ∠8) |
| Interior on the same side of the transversal | (∠3 and ∠5), (∠4 and ∠6) |
Properties:
(i) Vertically opposite angles are equal.
∠1 = ∠4, ∠2 = ∠3,
∠5 = ∠8, ∠6 = ∠7
(ii) Alternate interior angles are equal.
∠3 = ∠6 and ∠4 = ∠5
(iii) Alternate exterior angles are equal.
∠1 = ∠8 and ∠2 = ∠7
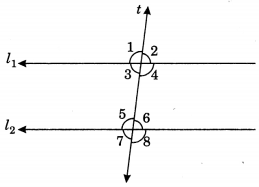
(iv) Corresponding angles are equal.
∠1 = ∠5, ∠2 = ∠6,
∠3 = ∠7, ∠4 = ∠8
(v) Sum of interior angle on the same sides of transversal is 180°.
∠3 + ∠5 = 180°, ∠4 + ∠6 =180°
(vi) Linear pairs are supplementary angles.
∠1 + ∠3 = 180°, ∠1 + ∠2 = 180°
∠2 + ∠4 = 180°, ∠3 + ∠4 = 180°
∠5 + ∠6 = 180°, ∠6 + ∠8 = 180°
∠7 + ∠8 = 180°, ∠5 + ∠7 = 180°