Free PDF Download of CBSE Maths Multiple Choice Questions for Class 12 with Answers Chapter 11 Three Dimensional Geometry. Maths MCQs for Class 12 Chapter Wise with Answers PDF Download was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Three Dimensional Geometry MCQs Pdf with Answers to know their preparation level.
Three Dimensional Geometry Class 12 Maths MCQs Pdf
1. The distance of point (2, 5, 7) from the x-axis is
(a) 2
(b) √74
(c) √29
(d) √53
Answer/Explanation
Answer: b
Explaination:
(b), as distance of point (2, 5, 7) from the x-axis is
![]()
2. P is a point on the line segment joining the points (3, 5, -1) and (6, 3, -2). If y-coordinate of point P is 2, then its x-coordinate will be
(a) 2
(b) \(\frac{17}{3}\)
(c) \(\frac{15}{2}\)
(d) -5
Answer/Explanation
Answer: c
Explaination:
(c), as let P divides the join of (3, 5, -1) and (6, 3, -2) in the ratio k : 1

3. Direction ratios of a line are 2, 3, -6. Then direction cosines of a line making obtuse angle with the y-axis are

Answer/Explanation
Answer: c
Explaination:
(c), as direction cosines of a line whose direction ratio are 2,3, -6 are \(\frac{2}{7}, \frac{3}{7}, \frac{-6}{7}\).
As angle with the y-axis is obtuse,
∴ cos β < 0,
Therefore direction ratios are \(\frac{-2}{7}, \frac{-3}{7}, \frac{6}{7}\).
4. A line makes angle α, β, γ with x-axis, y-axis and z-axis respectively then cos 2α + cos 2β + cos 2γ is equal to
(a) 2
(b) 1
(c) -2
(d) -1
Answer/Explanation
Answer: d
Explaination:

5. The equations of y-axis in space are
(a) x = 0, y = 0
(b) x = 0, z = 0
(c) y = 0, z = 0
(d) y = 0
Answer/Explanation
Answer: b
Explaination: (b), as on the y-axis, x-coordinate and z-coordinate are zeroes.
6. If the direction cosines of a line are \(\frac{k}{3}, \frac{k}{3}, \frac{k}{3}\), then value of k is
(a) k > 0
(b) 0 < k < 1.
(c) k = \(\frac{1}{3}\)
(d) k = ± 73
Answer/Explanation
Answer: d
Explaination:
![]()
7. Distance of plane \(\vec{r} \cdot(2 \hat{i}+3 \hat{i}-6 \hat{k})+2=0\), from origin is
(a) 2
(b) 14
(c) \(\frac{2}{7}\)
(d) –\(\frac{2}{7}\)
Answer/Explanation
Answer: c
Explaination:

![]()
8. Distance between planes
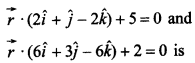

Answer/Explanation
Answer: c
Explaination:
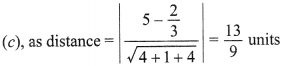
9. The line joining the points (0, 5, 4) and (1, 3, 6) meets XY-plane at the point ________ .
Answer/Explanation
Answer:
Explaination:
(-2, 9, 0), as line is \(\frac{x-1}{1}=\frac{y-3}{-2}=\frac{z-6}{2}=\lambda\)
General point on line is (λ + 1, -2λ + 3, 2λ + 6)
If it meets AT-plane, then 2λ + 6 = 0
⇒ λ = – 3
∴ Point is (-2, 9, 0)
10. A line makes angles α, β, γ with z-axis, x-axis and y-axis respectively. Then direction cosines of line are cos β, cos γ, cos α. State true or false.
Answer/Explanation
Answer:
Explaination: True, as direction cosines of a line are cosines of the angles which a line makes with x, y and z-axes respectively.
11. A line makes angles \(\frac{\pi}{4}, \frac{3 \pi}{4}\) with x-axis and y-axis respectively. Then the angle which it makes with z-axis can be ________ .
Answer/Explanation
Answer:
Explaination:
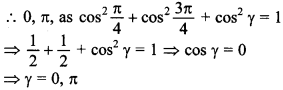
12. The vector equation of the line

State true or false.
Answer/Explanation
Answer:
Explaination:
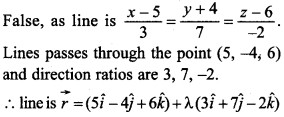
13. The Cartesian equation of a line AB is
![]()
Find the direction cosines of a line parallel to AB.
Answer/Explanation
Answer:
Explaination:

14. Find the direction cosines of the line passing through the following points: (-2, 4, -5), (1, 2, 3) [NCERT]
Answer/Explanation
Answer:
Explaination:
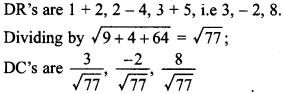
15. Find the Cartesian equation of the line which passes through the point (-2,4, -5) and is parallel to the line \(\frac { x+3 }{ 3 } =\frac { 4-y }{ 5 } =\frac { z+8 }{ 6 } \) [Delhi 2013]
Answer/Explanation
Answer:
Explaination:

16. Write the vector equation of the following line: \(\frac { x-5 }{ 3 } =\frac { y+4 }{ 7 } =\frac { 6-z }{ 2 } \)
Answer/Explanation
Answer:
Explaination:
The line passes through the point (5, -4, 6) and dr’s of the line are 3, 7, – 2.
∴ vector equation is
![]()
17. Write the Cartesian equation of the following line given in vector form:
![]()
Answer/Explanation
Answer:
Explaination:
Point through which line passes is (2, 1, -4) and dr’s: 1, – 1, – 1.
∴ Cartesian equation of line
![]()
18. What are the direction cosines of a line, which makes equal angles with the coordinate axes? [NCERT; Foreign 2011]
Answer/Explanation
Answer:
Explaination:

19. If the direction cosines of a given line are \(\frac{1}{k}, \frac{1}{k}, \frac{1}{k}\) then, find the value of k.
Answer/Explanation
Answer:
Explaination:
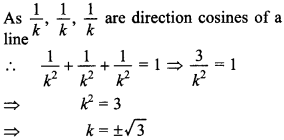
20. If a line makes angles 90° and 60° respectively with the positive directions of x and y axes, find the angle which it makes with the positive direction ofz-axis. [Delhi 2017]
Answer/Explanation
Answer:
Explaination:
Let angle with z-axis be γ.
cos²90° + cos²60° + cos² γ = 1
⇒ 0 + \(\frac{1}{4}\) + cos² γ = 1
⇒ cos² γ = \(\frac{3}{4}\)
cos γ = \(\pm \frac{\sqrt{3}}{2}\)
γ = 30°, 150°
21. Find the vector equation of the line passing through the point A(1, 2,-1) and parallel to the line 5x – 25 = 14 – 7y = 35z. [Delhi 2017]
Answer/Explanation
Answer:
Explaination:
Given line is 5x – 25 = 14 – 7y = 35z
⇒ 5(x – 5) = – 7(y – 2) = 35z
![]()
DR’s of line are 7, – 5 and 1
dr’s of line parallel to the given line are 7,-5, 1.
vector equation of line through the point (1, 2, – 1) and having dr’s 7,-5 and 1 is
![]()
22. Write the distance of the point (3, – 5, 12) from the x-axis. [Foreign 2017]
Answer/Explanation
Answer:
Explaination:
Distance of the point (3, – 5, 12) from the x-axis

23. Find the angle between the following pair of lines:
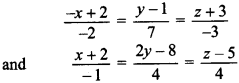
and check whether the lines are parallel or perpendicular. [Delhi 2011]
Answer/Explanation
Answer:
Explaination:
DR’s of lines are 2, 7, – 3 and – 1, 2, 4
As 2 × (- 1) + 7 × 2 – 3 × 4 = 0, so lines are perpendicular. Angle = 90°
24. The x-coordinate of a point on the line joining the points P(2, 2, 1) and Q(5, 1, -2) is 4. Find its z-coordinate. [AI2017]
Answer/Explanation
Answer:
Explaination:
Let point R(4, y, z) lies on the line joining P(2, 2, 1) and Q(5, 1, -2). Let R divides PQ in ratio k: 1

25. If P(1, 5, 4) and Q(4, 1, – 2), find the direction ratios of \(\overrightarrow{P Q}\).
Answer/Explanation
Answer:
Explaination:
Direction ratios of \(\overrightarrow{P Q}\) =4 – 1, 1 – 5 and -2 -4, i.e. 3, -4 and – 6.
26. The equations of a line are 5x – 3 = 15y + 7 = 3 – 10z. Write the direction cosines of the line. [All India]
Answer/Explanation
Answer:
Explaination:
The equation of a line are 5x – 3 = 15y + 7 = -10z + 3

27. Equation of the perpendicular drawn from the point with position vector \(2 \hat{i}- \hat{j}+ \hat{k}\) to the plane \(\vec{r} \cdot(\hat{i}-3 \hat{k})=5\) is ________ .
Answer/Explanation
Answer:
Explaination:

28. General equation of a plane passing through the intersection of two given

Answer/Explanation
Answer:
Explaination:

29. Cartesian equation of the plane
![]()
State true or false.
Answer/Explanation
Answer:
Explaination:

30. Find the distance of the point (2,3,4) from the plane
![]()
Answer/Explanation
Answer:
Explaination:
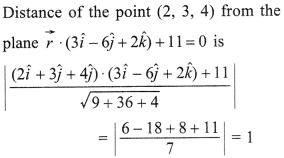
31. Write the intercept cut off by the plane 2x + y – z = 5 on the x-axis. [Delhi 2011]
Answer/Explanation
Answer:
Explaination:
For intercept on the x-axis, put y = 0 and z = 0
⇒ 2x = 5
⇒ x = \(\frac{5}{2}\)
∴ x-intercept = \(\frac{5}{2}\)
32. Find the distance of the plane 3x – 4y + 12z = 3 from the origin. [AI 2012]
Answer/Explanation
Answer:
Explaination:
![]()
33. Find the angle between the planes

Answer/Explanation
Answer:
Explaination:
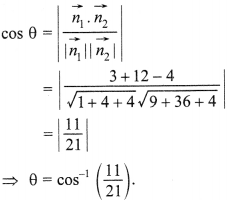
34. Find the distance between the planes 2x – y + 2z – 5 and 5x – 2.5y + 5z = 20. [AI 2017]
Answer/Explanation
Answer:
Explaination:
Planes are 2x – y + 2z = 5
⇒ 2x – y + 2z – 5 = 0
and 5x – 2.5y + 5z = 20
⇒ 2x – y + 2z – 8 = 0
![]()
35. A line passes through the point with position vector \(2 \hat{i}-3 \hat{j}+4 \hat{k}\) and is perpendicular to the plane \(\vec{r} \cdot(3 \hat{i}+4 \hat{j}-5 \hat{k})=7\). Find the
Answer/Explanation
Answer:
Explaination:

We hope the given Maths MCQs for Class 12 with Answers Chapter 11 Three Dimensional Geometry will help you. If you have any query regarding CBSE Class 12 Maths Three Dimensional Geometry MCQs Pdf, drop a comment below and we will get back to you at the earliest.