Free PDF Download of CBSE Maths Multiple Choice Questions for Class 12 with Answers Chapter 9 Differential Equations. Maths MCQs for Class 12 Chapter Wise with Answers PDF Download was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Differential Equations MCQs Pdf with Answers to know their preparation level.
Differential Equations Class 12 Maths MCQs Pdf
1. Order of differential equation correspon- ding to family of curves y = Ae2x + Be2x is ______ .
Answer/Explanation
Answer:
Explaination: 2, as there are two arbitrary constants and we have to differentiate twice.
2. The order of the differential equation corresponding to the family of curves y = c(x – c)², c is constant is ______ .
Answer/Explanation
Answer:
Explaination: One, as there is one arbitrary constant.
3. The degree of differential equation
![]()
is not defined. State true or false.
Answer/Explanation
Answer:
Explaination: Three, as equation cannot be represented as polynomial of derivatives.
4. If p and q are the degree and order of the differential equation
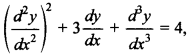
then the value of 2p – 3q is
(a) 7
(b) -7
(c) 3
(d) -3
Answer/Explanation
Answer: b
Explaination:
(b), as degree p = 1 and order q = 3
∴ 2p – 3q = 2 – 9 = -7
5. The degree of the differential equation
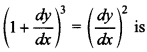
(a) 1
(b) 2
(c) 3
(d) 4
Answer/Explanation
Answer: c
Explaination:
(c), as differential equation is
![]()
Exponent of highest order derivative is 3.
6. The degree of the differential equation
![]()
(a) 1
(b) 2
(c) 3
(d) not defined
Answer/Explanation
Answer: d
Explaination:
(d), as equation cannot be represented as a polynomial of derivatives.
7. The order of the differential equation of all the circles of given radius 4 is
(a) 1
(b)2
(c) 3
(d) 4
Answer/Explanation
Answer: b
Explaination:
(b), as centre is arbitrary (h, k), two arbitrary constants so we have to differentiate twice to eliminate h, k
∴ order is 2.
8. Degree of the differential equation
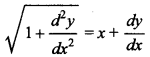
is not defined. State true or false.
Answer/Explanation
Answer:
Explaination:
False, as equation can be written as
![]()
Further it can be written as a polynomial of derivatives. 9.
9. Write the degree of the differential equation
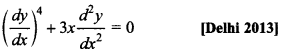
Answer/Explanation
Answer:
Explaination: Degree 1
10. Write the degree of the differential equation
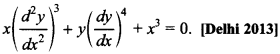
Answer/Explanation
Answer:
Explaination: Degree 3.
11. Find the value of m and n, where m and n are order and degree of differential equation

Answer/Explanation
Answer:
Explaination:
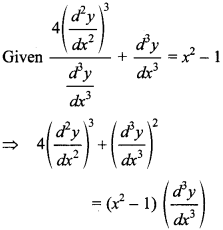
Order of differential equation (m) = 3
Degree of differential equation (n) = 2
12. Write the order and degree of the differential equation \(\frac{d y}{d x}+\sin \left(\frac{d y}{d x}\right)\) = 0. [HOTS]
Answer/Explanation
Answer:
Explaination:
Highest order derivative is \(\frac{dy}{dx}\). Hence, order of differential equation is 1. Equation cannot be written as a polynomial’ in derivatives. Hence, degree is not defined.
13. The differential equation of the family of lines passing through ongrn is
(a) y = mx
(b) \(\frac{dy}{dx}\) = m
(c) x dy – y dx = 0
(d) \(\frac{dy}{dx}\) = 0
Answer/Explanation
Answer: c
Explaination:
(c), as general equation of line through origin is
y = mx
⇒ \(\frac{dy}{dx}\) = m
Substituting in (i), we get dy
y = \(\frac{dy}{dx}\).x
⇒ x dy – y dx = 0
14. Find the differential equation representing the family of curves y = aebx + 5, where a and b are arbitrary constants. [CBSE 2018]
Answer/Explanation
Answer:
Explaination:
Consider y = aebx + 5
.On differentiating both sides, w.r.t, x
\(\frac{dy}{dx}\) = abebx + 5 = by …..(i)
Again differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}=b \cdot \frac{d y}{d x}\) …..(ii)
From (i) and (ii), eliminating b, we get
\(y \cdot \frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\) as required equation.
15. Form the differential equation representing the family of parabolas having vertex at origin and axis along positive direction of the x-axis. [NCERT; DoE]
Answer/Explanation
Answer:
Explaination:
General equation of parabola is y² = 4ax …..(i)
Differentiating, we get 2yy’ = 4a
⇒ yy’ = 2a.
Substituting in (i), we gety2 = 2xyy’.
16. Form the differential equation of the family of parabolas having vertex at the origin and axis along positive y-axis. [Delhi 2011]
Answer/Explanation
Answer:
Explaination:
x² = 4 ay
⇒ 2x = 4 ay’
⇒ \(\frac{x^{2}}{2 x}=\frac{4 a y}{4 a y^{\prime}}\)
⇒ xy’ – 2y = 0 is the required equation.
17. General solution of the differential equation log\(\frac{dy}{dx}\) = 2x +y is _______ .
Answer/Explanation
Answer:
Explaination:

18. Solve the differential equation \(\frac{dy}{dx}\) = ex – y + x3e-y.
Answer/Explanation
Answer:
Explaination:
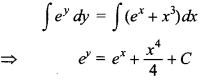
19. Find the particular solution of the differential equation \(\frac{dy}{dx}\) =y tanx, given that y= 1 when x = 0.
Answer/Explanation
Answer:
Explaination:
∫ \(\frac{dy}{y}\) = ∫tan x dx
⇒ log |y| = log|sec x| + log C
⇒ y = C sec x ….(i)
Given y = 1, x = 0
⇒ 1 = C sec 0
⇒ C = 1
∴ solution is y = sec x [from (i)]
20. Find the general solution of the differential equation \(\frac{dy}{dx}\) = \(\frac{x+1}{2-y}\), (y ≠ 2). [NCERT]
Answer/Explanation
Answer:
Explaination:

We hope the given Maths MCQs for Class 12 with Answers Chapter 9 Differential Equations will help you. If you have any query regarding CBSE Class 12 Maths Differential Equations MCQs Pdf, drop a comment below and we will get back to you at the earliest.