Matrices Class 12 Notes Maths Chapter 3

By going through these CBSE Class 12 Maths Notes Chapter 3 Matrices, students can recall all the concepts quickly.

Matrices Notes Class 12 Maths Chapter 3

Matrix (Definition): A matrix is defined as a rectangular array (arrangement) of numbers or functions.A
The matrices are denoted by capital letters as shown below:

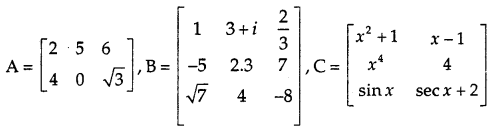
→ Elements: The numbers or functions in a matrix are called its elements. In matrix A; 2, 5, 6, 4, 0 and \(\sqrt{3}\) are the elements.

→ Row: The elements lying in a horizontal line form a row. Matrix B has 3 rows viz: first row is (1, 3 + 2i, \(\frac{2}{3}\)) is (-5, 2.3, 7) and third row is (\(\sqrt{7}\) 4 -8).

→ Column: The elements lying in a vertical line form a column. Matrix A has three columns viz: first column is \(\left(\begin{array}{l}
2 \\
4
\end{array}\right)\), second is \(\left(\begin{array}{l}
5 \\
0
\end{array}\right)\) and third is \(\left(\begin{array}{c}
6 \\
\sqrt{3}
\end{array}\right)\)

→ Order of matrix: A matrix, having m rows and n columns, is said to be of the order m × n. The matrix A is of order 2 × 3, B is of order 3 × 3 and C is of order 3 × 2.

In general, a matrix of order m × n, i.e., consisting of m rows and n columns is denoted by A = [a_ij]_m×n.

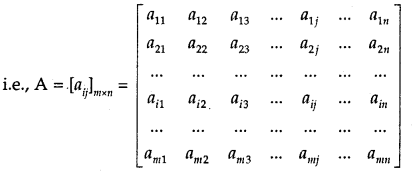
A number of elements in the matrix [a_ij]_m×n are m × n and nth element = a_ij is that element that lies in the ith row and jth column.

Types of matrices:
→ Square Matrix: If in a matrix, the number of rows is equal to the number of columns, then the matrix is called a square matrix.

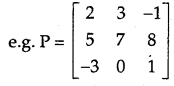
has 3 rows and 3 columns. Therefore, it is a square matrix.

In general, [a_ij]_n×n is a square matrix of order n. the elements a₁₁, a₂₂, a₃₃,…,a_ii…, a_nn are the elements of main diagonal. Thus, in the matrix P; 2, 7 and 1 are the diagonal elements.

→ Row Matrix: A matrix, which has one row is known as row matrix. [3 -1 i 2] is a row matrix, which has only one row.

→ Column Matrix: A matrix having one column is said to be is a column matrix.\(\left[\begin{array}{c}
-1 \\
3 \\
2
\end{array}\right]\) is a column matrix, since there is only one column in it.

→ Diagonal Matrix: A square matrix is called a diagonal matrix, if its non-diagonal elements are zero, i.e., a_ij = 0, when i ≠ 0, e.g. \(\left[\begin{array}{ll}
2 & 0 \\
0 & 1
\end{array}\right]\) is a diagonal matrix.

→ Scalar Matrix: It is a square matrix whose (a) diagonal elements are non-zero and equal (b) non-diagonals elements are zero, Le, a_ij = k ≠ 0 when j = j, a_ij = 0, when i ≠ j.\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 2
\end{array}\right]\) is scalar matrix.

→ Unit or Identity Matrix: It is a square matrix in which each diagonal element is 1. i.e., a_ij = 1 when i = j and aij = 0 when i ≠ j.\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) is an Identity or Unit matrix.

→ Zero Matrix or Null Matrix: A matrix, in which all the elements are equal to zero, is called the zero matrix.\(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\) is a zero matrix.

→ Comparable Matrices: Two matrices are said to be comparable, if they are of the same order. For example, \(\left[\begin{array}{ccc}
2 & 3 & -5 \\
4 & -2 & 6
\end{array}\right]\) and \(\left[\begin{array}{ccc}
i & 2 & x \\
3 & x^{2} & -1
\end{array}\right]\) are comparable matrices since each matrix is of order 2 × 3.

→ Equal Matrices: Two matrices are equal, if (a) they are of the same order (b) their corresponding elements are equal.

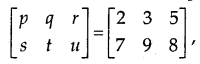
if p = 2, q = 3, r = 5, s = 7, t = 9 and u = 8.

OPERATIONS ON MATRICES:
→ Addition of Matrices: The sum of two matrices A and B of the same order is obtained by adding the corresponding elements. Thus,

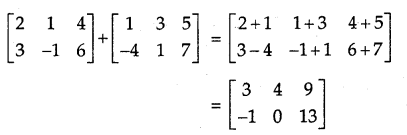
→ Multiplication of a Matrix by a Scalar: If a matrix A = [a_ij]_m×n is multiplied by a scalar k, then the product kA is obtained by multiplying each element of A, by k. For example,

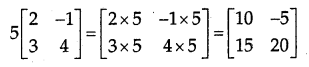
→ Negative of a Matrix: The negative of a matrix A = -A = (-1)A. For example,

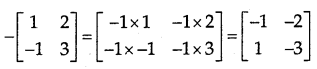
→ Difference of two Matrices: If A and B are the matrices of the same order, then A – B = A + (-1)B = Sum of matrices A and -B.

→ Properties of Matrices Addition: Let A, B, and C be the matrices of the same order m × n.
(a) The commutation Law: A + B = B + A
(b) The Association Law: (A + B) + C = A + (B + C)
(c) The Existence of Additive Identity: Let Omxn be null matrix of order m × n.
A + O_m×n = O_m×n + A = A.
(d) The Existence of Additive Inverse: Let A = [aij]m×n. We have an order matrix – A = [-a_ij]_m×n such that A + (-A) = A – A = O_m×n
-A is called the additive inverse of A or negative of A.

→ Properties of Scalar Multiplication of a Matrix
Let A and B be the matrices of the same order m × n. Then,
(a) k(A + B) = kA + kB
(b) (k + l)A = kA+ lA

→ Multiplication of Matrices
Two matrices A and B are conformable for multiplication if the Tiber of columns in A is equal to the number of rows in B.
If A = [a_ij]_m×n then B = [b_ij]_n×p and AB = [c_ij]_m×p
C_ij = (ij), the element of AB = sum of the products of the elements of the ith row of A with corresponding elements oi jth column of B. Here, (ith row of A) (jth column of B).

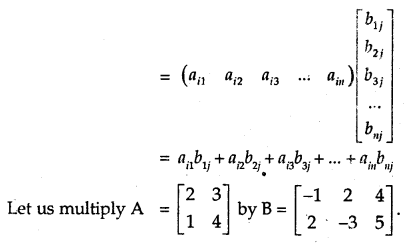
No. of columns in A = No. of rows in B = 2 ⇒ A and B are comformable for multiplication. Let AB = [C_ij]_2×3
c₁₁ = (I row of A) × (I column of B)
= \(\left[\begin{array}{ll}
2 & 3
\end{array}\right]\left[\begin{array}{c}
-1 \\
2
\end{array}\right]\) = 2 × (-1) + 3 × 2 = -2 + 6 = 4

c₁₂ = (I row of A) × (II column of B)
= \(\left[\begin{array}{ll}
2 & 3
\end{array}\right]\left[\begin{array}{c}
2 \\
-3
\end{array}\right]\) = 2 × 2 + 3 × (-3) = 4 – 9 = -5

c₁₃ = (I row of A) × (III column of B)
= \(\left[\begin{array}{ll}
2 & 3
\end{array}\right]\left[\begin{array}{l}
4 \\
5
\end{array}\right]\) = 2 × 4 + 3 × 5 = 8 + 15 = 23

c₂₁ = (II row of A) × (I column of B)
= \(\left[\begin{array}{ll}
1 & 4
\end{array}\right]\left[\begin{array}{c}
-1 \\
2
\end{array}\right]\) = 1 × (-1) + 4 × 2 = -1 + 8 = 7

c₂₂ = (II row of A) × (III column of B)
= \(\left[\begin{array}{ll}
1 & 4
\end{array}\right]\left[\begin{array}{c}
2 \\
-3
\end{array}\right]\) = 1 × 2 + 4 × (-3) = 2 – 12 = -10

c₂₃ = (II row of A) × (III column j B)
= \(\left[\begin{array}{ll}
1 & 4
\end{array}\right]\left[\begin{array}{l}
4 \\
5
\end{array}\right]\) =1 × 4 + 4 × 5 = 4 + 20 = 24

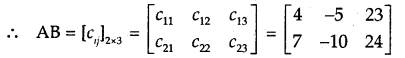
→ Properties of Multiplication of Matrices
(a) The Associative Law:
Let A = [a_ij]_m×n, B = [b_ij]_n×p and C = [c_ij]_p×q.
Then, (AB)C = A(BC)

(b) The Distributive Law:

1. If A = [a_ij]_m×n, B = [b_ij]_n×p and C = [c_ij]_p×q, then A(B + C) = AB + AC.
2. If A = [a_ij]_m×n, B = [b_ij]_n×p and C = [c_ij]_p×q, then (A + B)C = AC + BC.

(c) The Existence of Multiplicative Identity:
Let A be a square matrix. There exists an identity matrix I of the same order such that IA = AI = A.

TRANSPOSE OF A MATRIX:
(a) Definition: Let A = [a_ij]_m×n. The matrix obtained by interchanging the rows and columns of A is called transpose of A. It is denoted by A’ or A^T.
For A = [a_ij]_m×n A’ = [aij]_n×m.

(b) Properties of Transpose of a Matrix Let A and B be the two matrices. Then,

1. (A’)’ = A
2. (kA)’ = kA’, where k is a scalar
3. (A + B)’ = A’ + B’ (whenever A + B is defined)
4. (AB)’ = B’A’ (whenever AB is defined)

SYMMETRIC AND SKEW SYMMETRIC MATRICES:
→ Symmetric Matrix: A square matrix A = [a_ij]_n×n is called symmetric, if A’ = A, i.e., for a_ji = a_ij e.g. \(\left[\begin{array}{ccc}
2 & 3 & 4 \\
3 & 1 & 5 \\
4 & 5 & -1
\end{array}\right]\) is a symmetric matrix.

→ Skew Symmetric Matrix: A square matrix A = [aij]n×n is skew symmetric, if A’ = -A for all i, j or a_ji = – a_ij\(\left[\begin{array}{ccc}
0 & 2 & -3 \\
-2 & 0 & 4 \\
3 & -4 & 0
\end{array}\right]\) a skew symmetric matrix.

→ Properties: Let A be a square matrix with real elements.
(a) A + A’ is symmetric.
(b) A – A’ is skew symrrtetric.
(c) A square matrix can be expressed as the sum of the symmetric and skew-symmetric matrix, i.e.,
A = \(\frac{1}{2}\) (A + A’) + \(\frac{1}{2}\) (A – A’)

ELEMENTARY TRANSFORMATIONS OF A MATRIX:
→ Interchange of ith row and jth row is denoted by R_i ↔ R_j. Similarly, interchange of the ith column with the jth column is denoted by C_i ↔ C_j.

→ Multiplication of each element of ith row by k is represented as R_i → kR_j. and when the ith column is multiplied by k, it is represented as C_i → kC_j.

→ Let the element of the ith row of A be added to the corresponding elements of the jth row multiplied by k. It is denoted by R_i → R_i + kR_j.

Similarly, in the case of columns when elements of the ith column are added to the corresponding elements of the jth column multiplied by k, then C_i → C_j + kC_j.

INVERTIBLE MATRICES:
(a) Definition: Let A be a square matrix of order n. If there exists another square matrix B of the same order such that AB = BA = I_n, then A is said to be invertible and B is called the inverse of A. It is denoted by A^-1. ⇒ B = A^-1.

(b) Inverse of a Matrix by Elementary Operations
Let B = A^-1 be the inverse of A.
i.e., I_n = BA
Multiplying I_n by A^-1, we get
A^-1I_n = I_n A^-1 = (BA)A^-1 = B(AA^-1)
= BI_n = B.
⇒ A^-1 = B.
e.g. Let us find the inverse of \(\left[\begin{array}{ll}
1 & 2 \\
2 & 2
\end{array}\right]\) by elementary operations we have: \(\left[\begin{array}{ll}
1 & 2 \\
2 & 2
\end{array}\right]=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) A

By elementary transformation, we change the matrix \(\left[\begin{array}{ll}
1 & 2 \\
2 & 2
\end{array}\right]\) so that we get identity matrix.

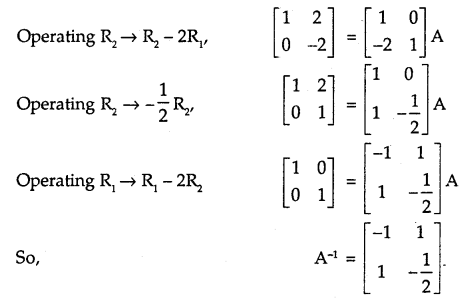
1. MATRIX
Def. A system of mn-numbers (real or complex) arranged in the form of an ordered set of m horizontal lines (called rows) and n vertical lines (called columns) is called an m x n matrix.

2. TYPES OF MATRICES

(i) Rectangular Matrix. Any m x n matrix (m≠n) is called a rectangular matrix.
(ii) Square Matrix. Any n x n matrix is called a square matrix of order n.
(iii) Row Matrix. Any 1 x n matrix is called a row matrix.
(iv) Column Matrix. Any m x 1 matrix is called a column matrix.
(v) Diagonal Matrix. A square matrix A = [a_ij ] is said to be a diagonal matrix if a_ij = 0 when i ≠ j.
(vi) Scalar Matrix. A diagonal matrix is said to be a scalar matrix if all its diagonal elements are equal.
(vii) Identity Matrix. A diagonal matrix is said to be an identity matrix if each of its diagonal elements is unity.
(viii) Zero Matrix. A matrix is said to be a zero matrix if each of its elements is zero.
(ix) Triangular Matrices.

(a) A square matrix A = [a_ij ] is said to be upper triangular matrix if a_ij =0 for i > j.
(b) A square matrix A = [a_ij ] is said to be lower triangular matrix if a_ij =0 for i < j.

3. EQUALITY OF MATRICES
Two matrices A = [a_ij ] and B = [b_ij] are said to be equal iff (i) they are of the same order (ii) their corresponding elements are equal.

4. OPERATIONS ON MATRICES

(i) Addition of Matrices.
Let A = [a_ij]_{m x n} and B = [b_ij]_{m x n} be two matrices. Then the sum A + B = C = [c_ij]_{m x n} , where c_ij + a_ij + b_ij for 1 ≤ i ≤ m, 1 ≤ j ≤ n

Key Point
Addition is defined only for matrices, which are of the same order.

(ii) Multiplication of a matrix by a scalar.
Let A be any m x n matrix and k be any scalar. Then m x n matrix obtained by multiplying each element by k is said to be scalar multiple of A by k and is denoted by kA or Ak.

(iii) Multiplication of Matrices.
Let A = [a_ij] be mxn matrix and B = [b_jk] be nxp matrix such that the number of columns of A equals the number of rows of B. Then matrix C = [c_ik] which is of the order m x p such that:

c_ik = \(\sum_{j=1}^{n} a_{i j} b_{j k}\) where i = 1,2, ….. m; p = 1, 2, 3,…………………k is called the product of the matrices A and B and is written as C = AB.

Key Point
Product AB is defined iff number of columns of A = number of rows of B.

5. TRANSPOSE OF A MATRIX
(i) Def. If A=[a_ij]_{m x n}, then the transpose of A, denoted by A’ (or A^t or A^T) is defined by n x m matrix obtained from A by writing the rows of A as columns and columns of A as rows in the same order.

(ii) Properties:

(a) (A’)’=A 1
(b) (A + B)’=A’+B’, A and B being of same type «
(c) (kA)’ = kA’, k being any scalar »
(d) (AB)’ = B’A’.

6. SYMMETRIC AND SKEW-SYMMETRIC MATRICES

(i) Symmetric Matrix.
Def. A square matrix A = [a_ij] is said to be symmetric if (i,j)th element is the same as its (j, i)th element.

Key Point is
A is symmetric if A’= A.

(ii) Skew-Symmetric Matrix.

A square matrix A = [a_ij] is said to be skew-symmetric if (i,j)th element is negative of its . (j, i)th element.

Key Point
A is skew-symmetric if A’ = – A.