ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test
Choose the correct answer from the given four options (1 to 12) :
Question 1.
\({ cot }^{ 2 }\theta -\frac { 1 }{ { sin }^{ 2 }\theta } \) is equal to
(a) 1
(b) -1
(c) sin2 θ
(d) sec2 θ
Solution:
\({ cot }^{ 2 }\theta -\frac { 1 }{ { sin }^{ 2 }\theta } \)
= \(\frac { { cos }^{ 2 }\theta }{ { sin }^{ 2 }\theta } -\frac { 1 }{ { sin }^{ 2 }\theta } \)
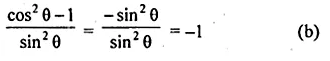
Question 2.
(sec2 θ – 1) (1 – cosec2 θ) is equal to
(a) – 1
(b) 1
(c) 0
(d) 2
Solution:
(sec2 θ – 1) (1 – cosec2 θ)
= \(\left( \frac { 1 }{ { cos }^{ 2 }\theta } -1 \right) \left( 1-\frac { 1 }{ { sin }^{ 2 }\theta } \right) \)
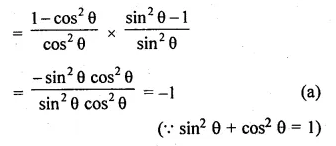
Question 3.
\(\frac { { tan }^{ 2 }\theta }{ 1+{ tan }^{ 2 }\theta } \) is equal to
(a) 2 sin2 θ
(b) 2 cos2 θ
(c) sin2 θ
(d) cos2 θ
Solution:
\(\frac { { tan }^{ 2 }\theta }{ 1+{ tan }^{ 2 }\theta } \)
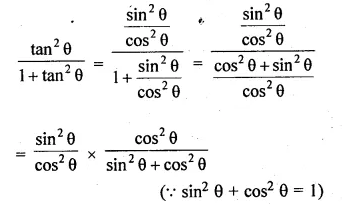
= \(=\frac { { sin }^{ 2 }\theta }{ 1 } ={ sin }^{ 2 }\theta \) (c)
Question 4.
(cos θ + sin θ)2 + (cos θ – sin θ)2 is equal to
(a) – 2
(b) 0
(c) 1
(d) 2
Solution:
(cos θ + sin θ)2 + (cos θ – sin θ)2
= cos2 θ + sin2 θ + 2 sin θ cos θ + cos2 θ + sin2 θ – 2 sin θ cos θ
= 2(sin2 θ + cos2 θ)
= 2 × 1 = 2 (d)
(∵ sin2 θ + cos2 θ = 1)
Question 5.
(sec A + tan A) (1 – sin A) is equal to
(a) sec A
(b) sin A
(c) cosec A
(d) cos A
Solution:
(sec A + tan A) (1 – sin A)
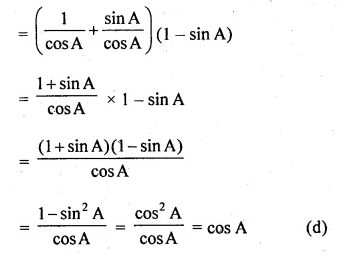
Question 6.
\(\frac { { 1+tan }^{ 2 }A }{ { 1+cot }^{ 2 }A } \) is equal to
(a) sec2 A
(b) – 1
(c) cot2 A
(d) tan2 A
Solution:
\(\frac { { 1+tan }^{ 2 }A }{ { 1+cot }^{ 2 }A } \)
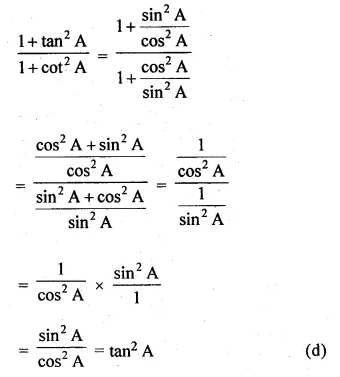
Question 7.
If sec θ – tan θ = k, then the value of sec θ + tan θ is
(a) \(1-\frac { 1 }{ k } \)
(b) 1 – k
(c) 1 + k
(d) \(\\ \frac { 1 }{ k } \)
Solution:
sec θ – tan θ = k
\(\frac { 1 }{ cos\theta } -\frac { sin\theta }{ cos\theta } =k\)
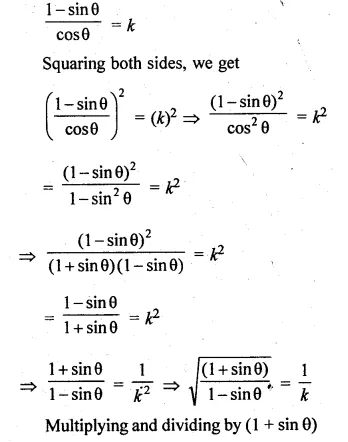
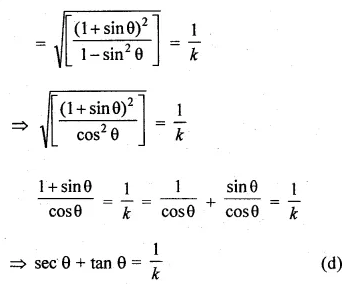
Question 8.
Which of the following is true for all values of θ (0° < θ < 90°):
(a) cos2 θ – sin2 θ = 1
(b) cosec2 θ – sec2 θ = 1
(c) sec2 θ – tan2 θ = 1
(d) cot2 θ – tan2 θ = 1
Solution:
∴ sec2 θ – tan2 θ = 1 is true for all values of θ as it is an identity.
(0° < θ < 90°) (c)
Question 9.
If θ is an acute angle of a right triangle, then the value of sin θ cos (90° – θ) + cos θ sin (90° – θ) is
(a) 0
(b) 2 sin θ cos θ
(c) 1
(d) 2 sin2 θ
Solution:
sin θ cos (90° – θ) + cos θ sin (90° – θ)
= sin θ sin θ + cos θ cos θ
{ ∵ sin(90° – θ) = cosθ, cos (90° – θ) = sin θ }
= sin2 θ + cos2 θ = 1 (c)
Question 10.
The value of cos 65° sin 25° + sin 65° cos 25° is
(a) 0
(b) 1
(b) 2
(d) 4
Solution:
cos 65° sin 25° + sin 65° cos 25°
= cos (90° – 25°) sin 25° + sin (90° – 25°) cos 25°
= sin 25° . sin 25° + cos 25° . cos 25°
= sin2 25° + cos2 25°
( ∵ sin2 θ + cos2 θ = 1)
= 1 (b)
Question 11.
The value of 3 tan2 26° – 3 cosec2 64° is
(a) 0
(b) 3
(c) – 3
(d) – 1
Solution:
3 tan2 26° – 3 cosec2 64°
= 3 tan2 26° – 3 cosec (90° – 26°)
= 3 tan2 26° – 3 sec2 26°

Question 12.
The value of \(\frac { sin({ 90 }^{ O }-\theta )sin\theta }{ tan\theta } -1 \) is
(a) – cot θ
(b) – sin2 θ
(c) – cos2 θ
(d) – cosec2 θ
Solution:
\(\frac { sin({ 90 }^{ O }-\theta )sin\theta }{ tan\theta } -1 \)
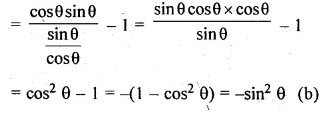
We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS, drop a comment below and we will get back to you at the earliest.