ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Find the A.P. whose nth term is 7 – 3K. Also find the 20th term.
Solution:
T_n = 7 – 3n
Giving values 1, 2, 3, 4, … to n, we get
T₁ = 7 – 3 x 1 = 7 – 3 = 4
T₂ = 7 – 3 x 2 = 7 – 6 = 1
T₃ = 7 – 3 x 3 = 7 – 9 = -2
T₄ = 7 – 3 x 4 = 7 – 12 = -5
T₂₀ = 7 – 3 x 20 = 7 – 60 = -53
A.P. is 4, 1, -2, -5, …
20th term = -53

Question 2.
Find the indicated terms in each of following A.P.s:
(i) 1, 6, 11, 16, …; a₂₀
(ii) – 4, – 7, – 10, – 13, …, a₂₅, a_n
Solution:
(i) 1, 6, 11, 16, …
Here, a = 1, d = 6 – 1 – 5
a₂₀ = a + (n – 1 )d
= 1 + (20 – 1) x 5
= 1 + 19 x 5
= 1 + 95
= 96

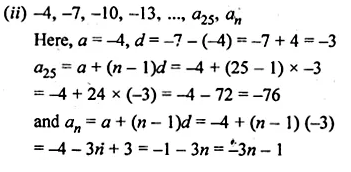
Question 3.
Find the nth term and the 12th term of the list of numbers: 5, 2, – 1, – 4, …
Solution:
5, 2, -1, -4, …
Here, a = 5 d = 2 – 5 = -3
(i) T_n = a + (n – 1)d
= 5 + (n – 1) (-3)
= 5 – 3n + 3
= 8 – 3n
(ii) T₁₂ = a + 11d
= 5 + 11(-3)
= 5 – 33
= -28

Question 4.
Find the 8th term of the A.P. whose first term is 7 and common difference is 3.
Solution:
First term (a) = 7
and common difference (d) = 3
A.P. = 7, 10, 13, 16, 19, …
T₈ = a + (n – 1)d
= 7 + (8 – 1) x 3
= 7 + 7 x 3
= 7 + 21
= 28

Question 5.
(i) If the common difference of an A.P. is – 3 and the 18th term is – 5, then find its first term.
(ii) If the first term of an A.P. is – 18 and its 10th term is zero, then find its common difference.
Solution:
(i) Common difference (d) = -3
T₁₈ = -5
a + (n – 1 )d = Tn
a + (18 – 1) (-3) = -5

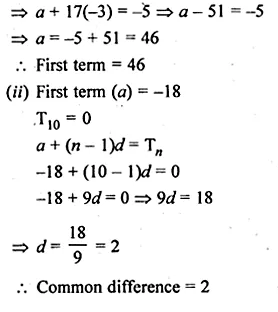
Question 6.
Which term of the A.P.
(i) 3, 8, 13, 18, … is 78?
(ii) 7, 13, 19, … is 205 ?
(iii) 18, \(15 \frac { 1 }{ 2 } \), 13, … is – 47 ?
Solution:
(i) 3, 8, 13, 18, … is 78
Let 78 is nth term
Here, a = 3, d = 8 – 3 = 5

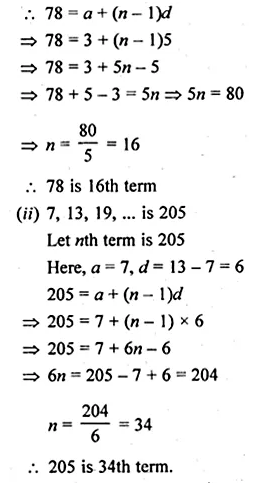
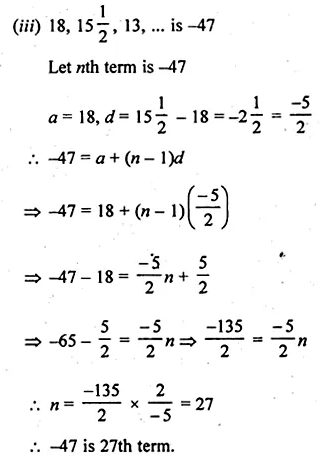
Question 7.
(i) Check whether – 150 is a term of the A.P. 11, 8, 5, 2, …
(ii) Find whether 55 is a term of the A.P. 7, 10, 13, … or not. If yes, find which term is it.
(iii) Is 0 a term of the A.P. 31,28, 25,…? Justify your answer.
Solution:
(i) A.P. is 11, 8, 5, 2, …
Here, a = 11, d = 8 – 11 = -3
Let -150 = n, then

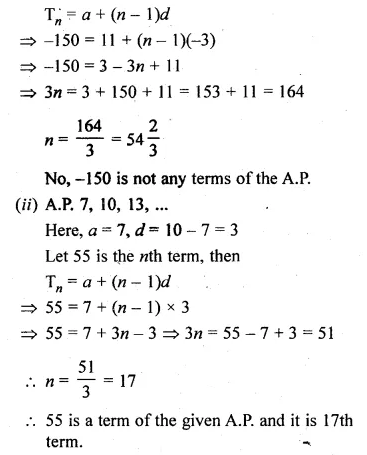
Question 8.
(i) Find the 20th term from the last term of the A.P. 3, 8, 13, …, 253.
(ii) Find the 12th from the end of the A.P. – 2, – 4, – 6, …; – 100.
Solution:
(i) A.P. is 3, 8, 13, …, 253
12th term from the end
Last term = 253
Here, a = 3, d = 8 – 3 = 5

Question 9.
Find the sum of the two middle most terms of the A.P.
\(-\frac { 4 }{ 3 } ,-1,-\frac { 2 }{ 3 } ,…,4\frac { 1 }{ 3 } \)
Solution:
Given
A.P. is \(-\frac { 4 }{ 3 } ,-1,-\frac { 2 }{ 3 } ,…,4\frac { 1 }{ 3 } \)

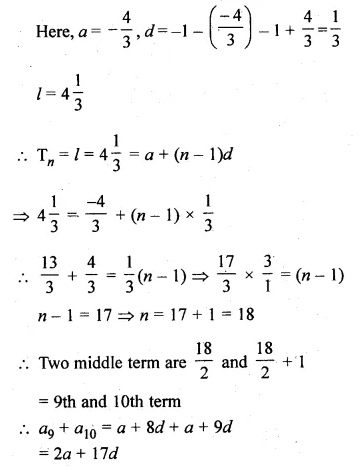
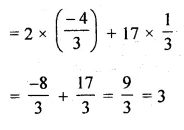
Question 10.
Which term of the A.P. 53, 48, 43,… is the first negative term ?
Solution:
Let nth term is the first negative term of the A.P. 53, 48, 43, …
Here, a = 53, d = 48 – 53 = -5
.’. T_n = a + (n – 1 )d
= 53 + (n – 1) x (-5)
= 53 – 5n + 5
= 58 – 5n
5n = 58
\(n= \frac { 58 }{ 5 } \)
= \(11 \frac { 3 }{ 5 } \)
∴ 12th term will be negative.

Question 11.
Determine the A.P. whose fifth term is 19 and the difference of the eighth term from the thirteenth term is 20.
Solution:
In an A.P.,
T₅ = 19
T₁₃ – T₈ = 20
Let a be the first term and d be the common difference

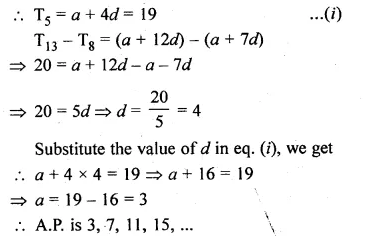
Question 12.
Determine the A.P. whose third term is 16 and the 7th term exceeds the 5th term by 12
Solution:
T₃ = 16
T₇ – T₅ = 12
Let a be the first term and d be the common difference

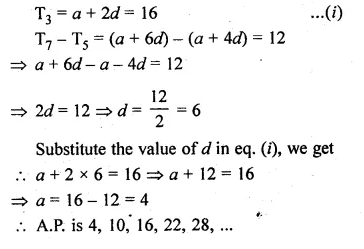
Question 13.
Find the 20th term of the A.P. whose 7th term is 24 less than the 11th term, first term being 12.
Solution:
T₁₁ – T₇ = 24
a= 12
Let a be the first term and d be the common difference, then
(a + 10d) – (a + 6d) = 24

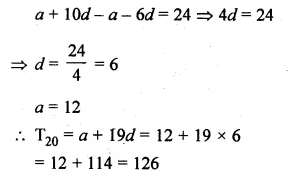
Question 14.
Find the 31st term of an A.P. whose 11th term is 38 and 6th term is 73.
Solution:
T₁₁ = 38, T₆ = 73
Let a be the first term and d be the common difference, then
a + 10d = 38..(i)
a + 5d = 73…(ii)

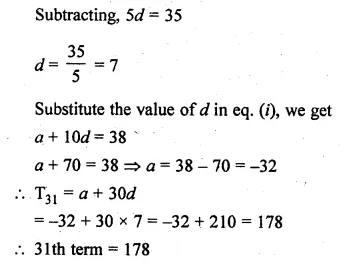
Question 15.
If the seventh term of an A.P. is \(\\ \frac { 1 }{ 9 } \) and its ninth term is \(\\ \frac { 1 }{ 7 } \), find its 63rd term.
Solution:
a₇ = \(\\ \frac { 1 }{ 9 } \)
⇒ a + 6d = \(\\ \frac { 1 }{ 9 } \) ….(i)
a₉ = \(\\ \frac { 1 }{ 7 } \)
⇒ a + 8d = \(\\ \frac { 1 }{ 7 } \)……(ii)

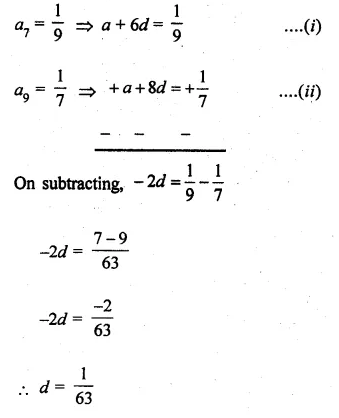
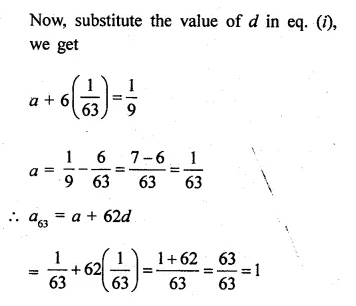
Question 16.
(i) The 15th term of an A.P. is 3 more than twice its 7th term. If the 10th term of the A.P. is 41, find its nth term.
(ii) The sum of 5th and 7th terms of an A.P. is 52 and the 10th term is 46. Find the A.P.
(iii) The sum of 2nd and 7th terms of an A.P. is 30. If its 15th term is 1 less than twice its 8th term, find the A.P.
Solution:
(i) Let a be the first term and d be a common difference.
We have,



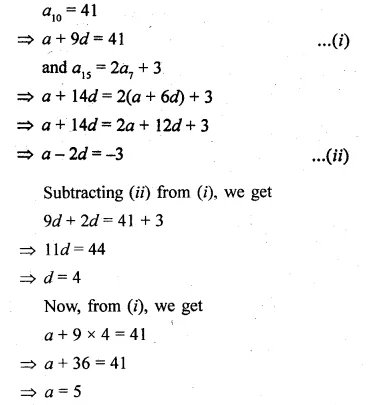
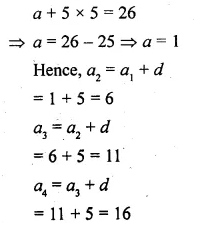
∴ The A.P formed is 1, 6, 11, 16,….

Question 17.
If 8th term of an A.P. is zero, prove that its 38th term is triple of its 18th term.
Solution:
T₈ = 0
To prove that T₃₈ = 3 x T₁₈
Let a be the first term and d be the common difference

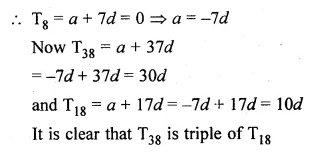
Question 18.
Which term of the A.P. 3, 10, 17,… will be 84 more than its 13th term?
Solution:
A.P. is 3, 10, 17, …
Here, a = 3, d – 10 – 3 = 7
T₁₃ = a + 12d
= 3 + 12 x 7
= 3 + 84
= 87

Question 19.
If the nth terms of the two A.g.s 9, 7, 5, … and 24, 21, 18, … are the same, find the value of n. Also, find that term
Solution:
nth term of two A.P.s 9, 7, 5,… and 24, 21, 18, … are same
In the first A.P. 9, 7, 5, …
a = 9 and d = 7 – 9 = -2
T_n = a + (n – 1)d
= 9 + (n – 1)(-2)

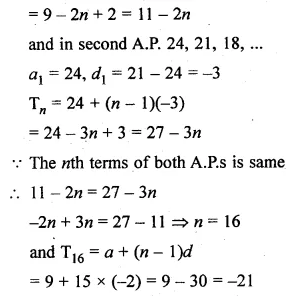
Question 20.
(i) How many two digit numbers are divisible by 3 ?
(ii) Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
(iii) How many numbers lie between 10 and 300, which when divided by 4 leave a remainder 3?
Solution:
(i) Two digits numbers divisible by 3 are
12, 15, 18, 21, …, 99
Here, a = 13, d = 15 – 12 = 3 and l = 99
Let number divisible by 3 and n

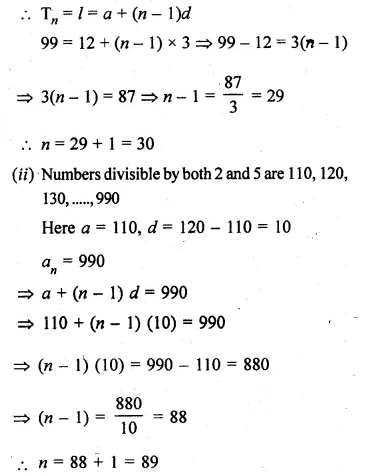
Question 21.
If the numbers n – 2, 4n – 1 and 5n + 2 are in A.P., find the value of n.
Solution:
n – 2, 4n – 1 and 5n + 2 are in A.P.
∴ 2(4n – 1) = n – 2 + 5n + 2
8n – 2 = 6n
⇒ 8n – 6n = 2
⇒ 2n = 1
⇒ \(n \frac { 2 }{ 2 } \) = 1
∴ n = 1

Question 22.
The sum of three numbers in A.P. is 3 and their product is – 35. Find the numbers.
Solution:
Sum of three numbers which are in A.P. = 3
Their product = -35
Let three numbers which are in A.P.
a – d, a, a + d
a – d + a + a + d = 3
⇒ 3a = 3 ,
⇒ a = \(\\ \frac { 3 }{ 3 } \) = 1

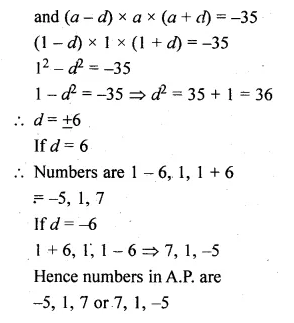
Question 23.
The sum of three numbers in A.P. is 30 and the ratio of first number to the third number is 3 : 7. Find the numbers.
Solution:
Sum of three numbers in A.P. = 30
Ratio between first and the third number = 3 : 7
Let numbers be
a – d, a, a + d, then
a – d + a + a + d = 30

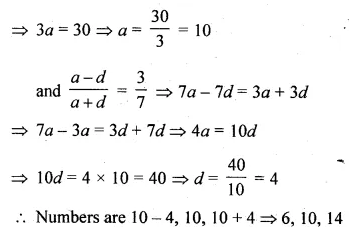
Question 24.
The sum of the first three terms of an A.P.is 33. If the product of the first and the third terms exceeds the second term by 29, find the A.P.
Solution:
Let the three numbers in A.P. are
a – d, a, a + d
Now, a – d + a + a + d = 33
⇒ 3a = 33
⇒ a = \(\\ \frac { 33 }{ 3 } \) = 11

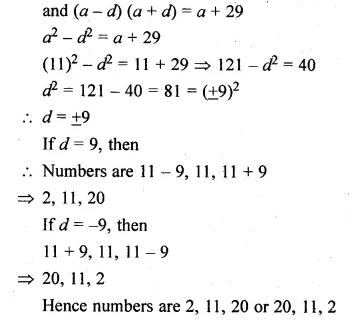
Question 25.
A man starts repaying a loan as first instalment of Rs 500. If he increases the instalment by Rs 25 every month, what,amount will he pay in the 30th instalment?
Solution:
First instalment of loan = Rs 500
Increases Rs 25 every month
Here, a = 500, d = 25
Total instalments (n) = 30
We have to find T₃₀
T₃₀ = a + (n – 1 )d = a + 29d
= 500 + 29 x 25
= 500 + 725
= Rs 1225

Question 26.
Ramkali saved Rs 5 in the first week of a year and then increased her savings by Rs 1.75. If in the rcth week, her weekly savings become Rs 20.75, find n.
Solution:
Savings in the first week = Rs 5
Increase every week = Rs 1.75
No. of weeks = n

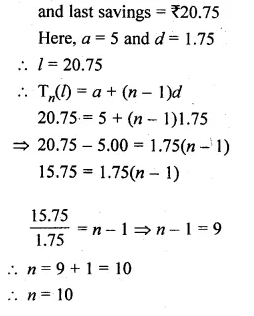
Question 27.
Justify whether it is true to say that the following are the nth terms of an A.P.
(i) 2n – 3
(ii) n² + 1
Solution:
(i) 2n – 3
Giving the some difference values to n such as 1, 2, 3, 4, … then
2 x 1 – 3 = 2 – 3 = -1
2 x 2 – 3 = 4 – 3 = 1
2 x 3 – 3 = 6 – 3 = 3
2 x 4 – 3 = 8 – 3 = 5

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.